2.2: Solución mediante gráficos

Última actualización
Guardar como PDF

Page ID: 111867

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

En cursos anteriores se cubre la solución de ecuaciones lineales, generalmente separando las variables y constantes en lados opuestos de la ecuación para aislar la variable. En el capítulo anterior examinamos la solución de ecuaciones cuadráticas, en las que la variable se aísla utilizando la técnica de completar el cuadrado. La mayor diferencia entre estos métodos de solución es que, en la resolución de ecuaciones cuadráticas, debemos lidiar con varias potencias diferentes de la variable lo que dificulta considerablemente el aislamiento de la variable. Existen fórmulas como la fórmula cuadrática disponibles para resolver$\left(x^{4}\right)$ ecuaciones cúbicas$\left(x^{3}\right)$ y cuárticas, sin embargo estas fórmulas son algo engorrosas y arcaicas. El método principal para resolver eqauciones de grado superior a 2 es la solución mediante gráficos o por algoritmo.

Solución por algoritmo es un proceso muy interesante ya que hay muchos algoritmos diferentes disponibles. Qué algoritmo es el más apropiado a menudo depende de los tipos de ecuaciones que se resuelvan y de la tecnología disponible para resolverlas. Dos tipos principales de algoritmos que se basan en la representación grafincal de una ecuación se llaman “Doble posición falsa” y “El método Newton-Raphson”. Muchas piezas de teconolgia comúnmente disponibles utilizan uno de estos métodos. ya que tenemos calculadoras gráficas disponibles para nosotros, nos centraremos en la solución graficando.

Ya sea usando una calculadora gráfica TI (Texas Instruments) o Casio, o una ustilidad gráfica basada en software como Graph o Desmos, la solución de estas ecuaciones se enfoca en encontrar las$x$ -intercepciones de la gráfica ya que aquí es donde el$y$ valor es 0. Los procesos específicos para resolver ecuaciones utilizando cada una de estas diferentes herramientas serán cubiertos en clase.
Ejemplo
Resolver para$x$
$x^{3}-3 x^{2}=2 x-7$
El primer paso es mover todos los términos a un lado de la ecuación y ponerlos iguales a cero.
$x^{3}-3 x^{2}-2 x+7=0$

Después graficamos la función y buscamos qué$x$ valores harán que el$y$ valor sea igual a 0
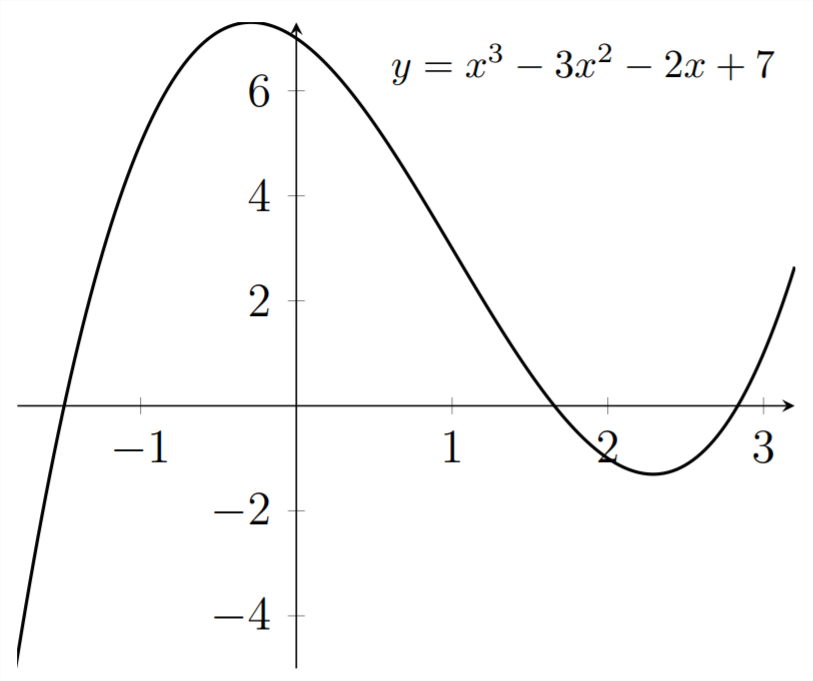
$clipboard_e33fa1feef9e5c0bb076eb8723f099773.png$
En esta gráfica, podemos ver tres raíces, o$x$ -intercepciones, donde la gráfica cruza el$x$ eje -eje. Estos son los$x$ -valores que hacen que el$y$ -valor sea igual a$0 .$ Podemos utilizar la tecnología disponible para encontrar estos$x$ -valores.
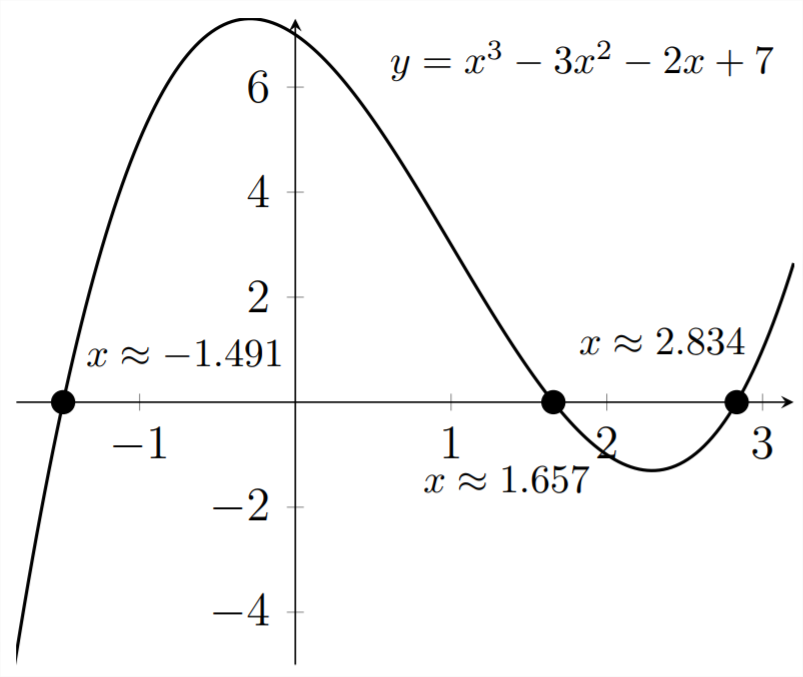
$clipboard_ec536203a344e401ed59a4b80b17e9690.png$
Entonces, podemos ver que las soluciones a la eqaución$x^{3}-3 x^{2}-2 x+7=0$ son$x \approx-1.491,1.657,2.834.$
Podemos verificar estas respuestas enchufándolas de nuevo en la ecuación original.

\ [
\ begin {aligned}
(-1.491) ^ {3} -3 * (-1.491) ^ {2} -2 * (-1.491) +7 &=-3.3146-3 * 2.223+2.982+7\\
&=-3.3146-6.669+2.982+7\\
&=-0.0016
\ end {alineado}
\]
El resultado no es exactamente 0 ya que nuestras respuestas tienen ha sido redondeado al lugar 1000. Si quisiéramos una mayor precisión, entonces deberíamos incluir mayor precisión en el valor de nuestras respuestas.
\ [
\ begin {alineado}
(1.657) ^ {3} -3 * (1.657) ^ {2} -2 * (1.657) +7 &=4.5495-3 * 2.7456-3.314+7\\
&=4.5495-8.2368-3.314+7\\
&=-0.0013
\ end {alineado}
\]
y
\ [
\ begin {alineado}
(2.834) ^ {3} -3 * (2.834) ^ {2} -2 * (2.834) +7 &=22.7614-3 * 8.03155-5.668+7\\
&=22.7614-24.09465-5.668+7\\
&=-0.00125
\ end {alineado}
\]

Ejercicios 2.2
Resolver para$x$
1)$\quad 3 x^{3}-7 x^{2}-x+1=0$
2)$\quad 24 x^{4}+5 x^{2}-13 x+3=0$
3)$\quad 2 x^{3}-2 x^{2}-28 x+51=0$
4)$\quad 2 x^{3}+5 x^{2}-15 x+7=0$
5)$\quad x^{4}-4 x^{3}+x^{2}+6 x+1=0$
6)$\quad x^{4}+2 x^{3}+x^{2}-x-6=0$
7)$\quad x^{4}-5 x^{3}-3 x^{2}+17 x-9=0$
8)$\quad 2 x^{3}-5 x-3=0$
9)$\quad x^{4}-4 x^{3}-7 x^{2}-36 x-18=0$
10)$\quad 6 x^{3}-25 x^{2}+21 x+10=0$
11)$\quad 2 x^{4}-5 x^{3}+x^{2}+4 x-2=0$
12)$\quad x^{4}+x^{3}-5 x^{2}+x-4=0$