2.4: Solución de las Desigualdades Racionales por Gráfica

Última actualización
Guardar como PDF

Page ID: 111895

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

En la sección anterior, vimos cómo resolver desigualdades polinomiales mediante la representación gráfica. En esta sección, utilizaremos métodos similares para resolver desigualdades racionales. Las desigualdades racionales implican proporciones de polinomios o fracciones. Debido a que este tipo de problemas involucran fracciones, las gráficas de las funciones con las que trabajamos tendrán lo que se conoce como asíntotas. Esta palabra proviene de una raíz griega que tiene que ver con dos líneas que se acercan muy entre sí pero que nunca se encuentran.

Las asíntotas verticales de una gráfica aparecerán en lugares donde la expresión original tenga un denominador cero. Esto significa que la función no está definida en esos$x$ valores y así, en lugar de tener un$y$ valor en ese punto, la gráfica tiene una asíntota.

Ejemplo
A continuación se muestra una gráfica de la función$y=\frac{x+2}{x-1}$
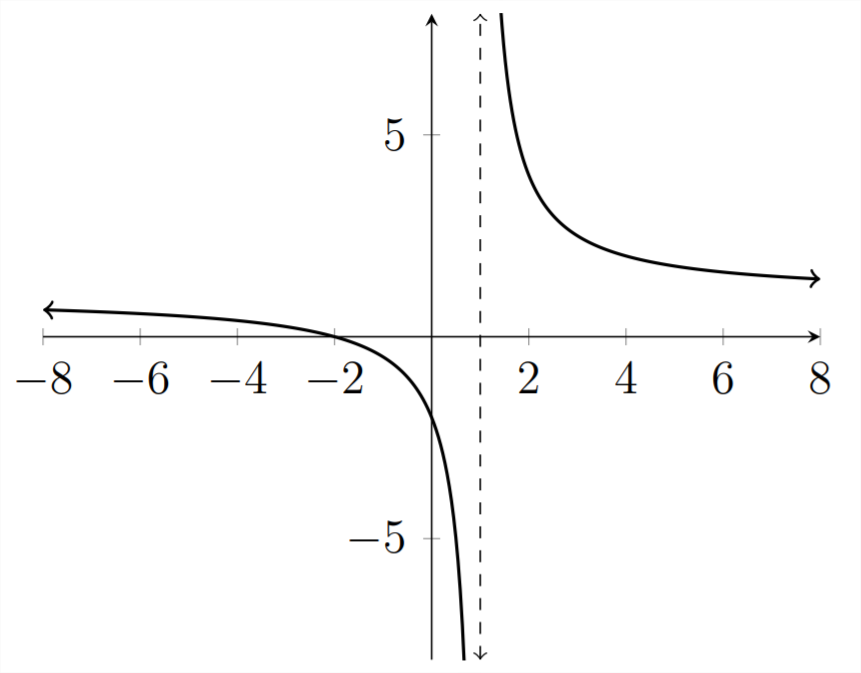
$clipboard_e8b5be7579424cdf40d488fe69acc33b2.png$
En lugar de tener un$y$ valor en el punto donde$x=1$, la línea punteada indica la asíntota donde la función no está definida. En la sección anterior, nos interesó encontrar las raíces de la función porque estos son los lugares donde$y=0,$ y pueden ser los puntos de división entre donde los$y$ valores son mayores que cero$(y>0)$ y donde los$y$ valores son menores que cero$(y<0)$

La importancia de las asíntotas en el análisis de las funciones racionales es que, al igual que las raíces, éstas representan$x$ valores que pueden ser los puntos de división entre dónde$y>0$ y dónde$y<0$

Ejemplo
Resolver la desigualdad dada.
$\frac{2}{x-3}>0$
Primero examinamos la gráfica:
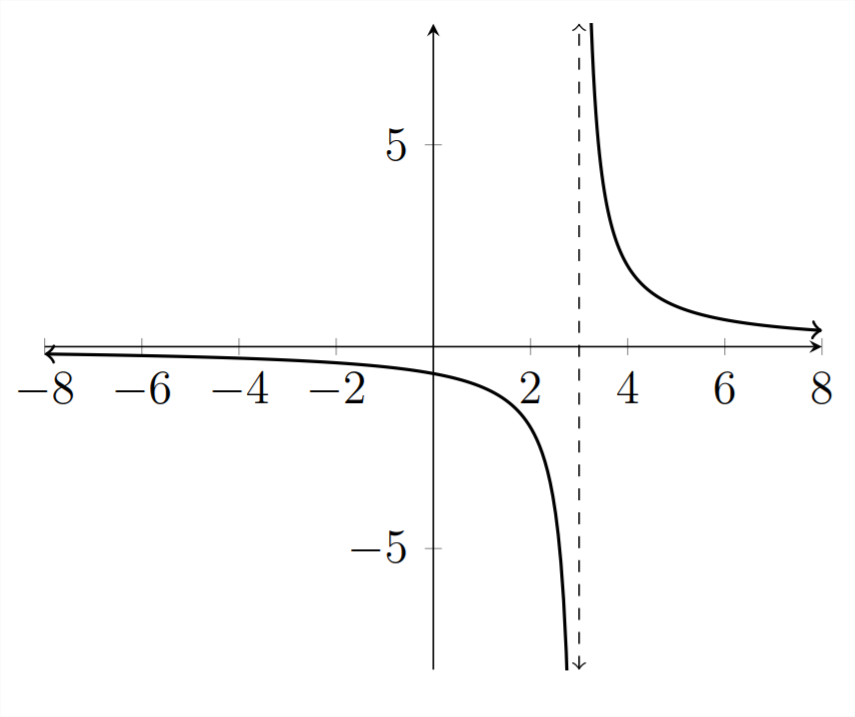
$clipboard_e7b47bfaba055a7809f9d294d419ab03a.png$

Observe que la asíntota para esta gráfica se produce en el valor$x=3,$ porque este es el$x$ valor que crea un denominador cero. También observe que los$y$ valores cambian de ser negativos a ser positivos a través de la asíntota.

No hay raíces para esta función porque no hay$x$ valores que hagan$y=0$ Para que una fracción sea cero, el numerador debe ser igual a cero. En este ejemplo el numerador es 2 y ningún valor de lo$x$ hará igual a cero. Por lo tanto, el único punto divisorio posible en la gráfica es$x=3,$ y la solución a la desigualdad es$x>3$

Ejemplo
Resolver la desigualdad dada.
$\frac{x-2}{x-3}>0$
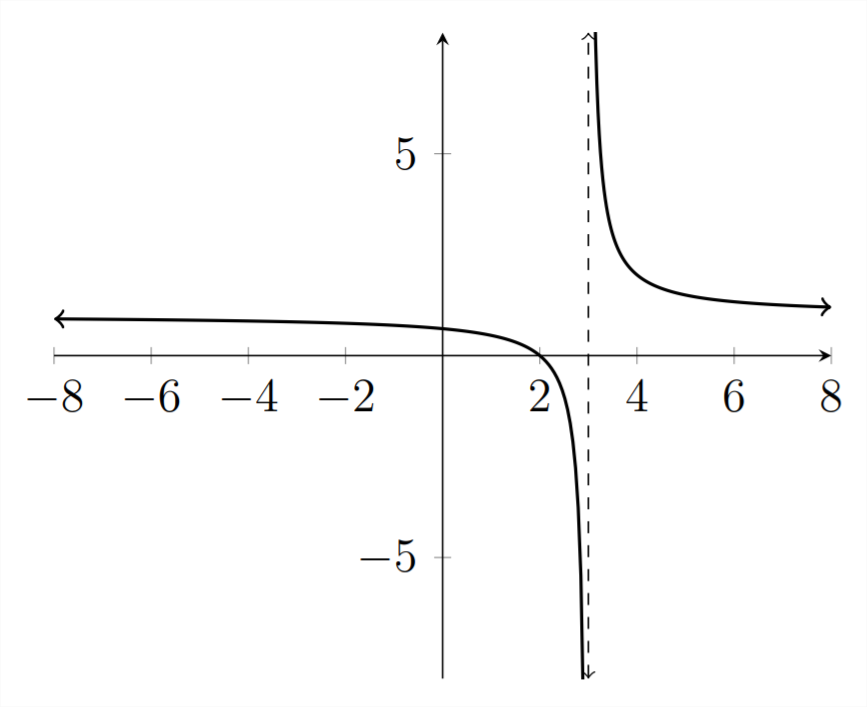
$clipboard_e4cb4d84afd9db47405f3ee30cf9ebecf.png$
En esta desigualdad, nuevamente hay una asíntota en$x=3,$ pero también hay una raíz en el valor$x=2,$ porque cuando$x=2 . y=\frac{2-2}{2-3}=\frac{0}{-1}=0 .$ Así tenemos dos puntos divisorios a considerar,$x=2$ y$x=3 .$ Podemos ver en la gráfica que $y>0$pues$x<2$ o$x>3,$ así esa es la solución a la desigualdad dada.

Ejemplo
Resolver la desigualdad dada.
$\frac{x^{2}-2}{x-3}>0$
En este problema, tenemos la misma asíntota que los dos problemas anteriores:$x=$
3. No obstante, en esta desigualdad, hay dos raíces, porque hay dos$x$ valores que hacen que el numerador sea igual a cero.
$x^{2}-2=0$significa eso$x^{2}=2$ y$x=\pm \sqrt{2} \approx \pm 1.414$
Podemos ver estas raíces en la gráfica.
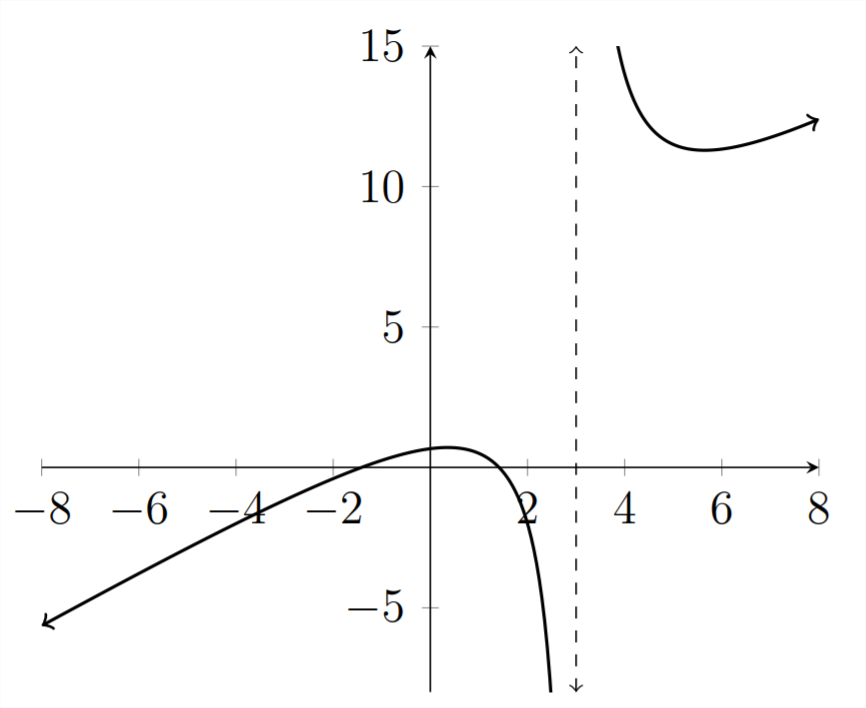
$clipboard_eb2306569ea50055c456320b49314925d.png$
En la gráfica anterior, podemos ver la asíntota en$x=3$ y las dos raíces en$x \approx 1.414,-1.414$
Los$x$ valores que hacen$y>0$ son$-1.414<x<1.414$ OR$x>3$

Ejemplo
Resolver la desigualdad dada.
$\frac{x-2}{x^{2}-3}>0$
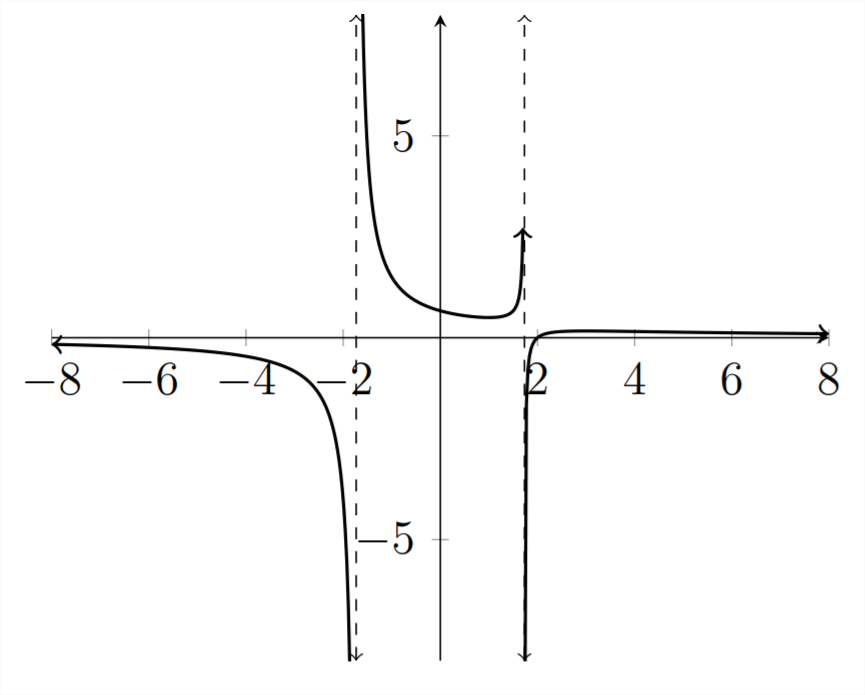
$clipboard_e08e2d260d00d03e93dbc53f8309b1e46.png$
Las raíces para esta función son los$x$ valores que hacen que el numerador sea igual a cero:
$x-2=0,$ por lo tanto$x=2,$ y podemos ver esta raíz en la gráfica.

Las asíntotas para la función son los$x$ valores que hacen que el denominador sea igual a
cero:
$x^{2}-3=0$ significa que$x^{2}=3$ y$x=\pm \sqrt{3} \approx \pm 1.732$

$clipboard_e0ba49fcb9c6b107b8ce7bf2168c0702c.png$
Por lo tanto la solución para la desigualdad dada es:
$-1.732<x<1.732$ O$x>2$
Ejemplo
Resolver la desigualdad dada
$\frac{5 x+1}{x^{2}+3 x-4}<0$

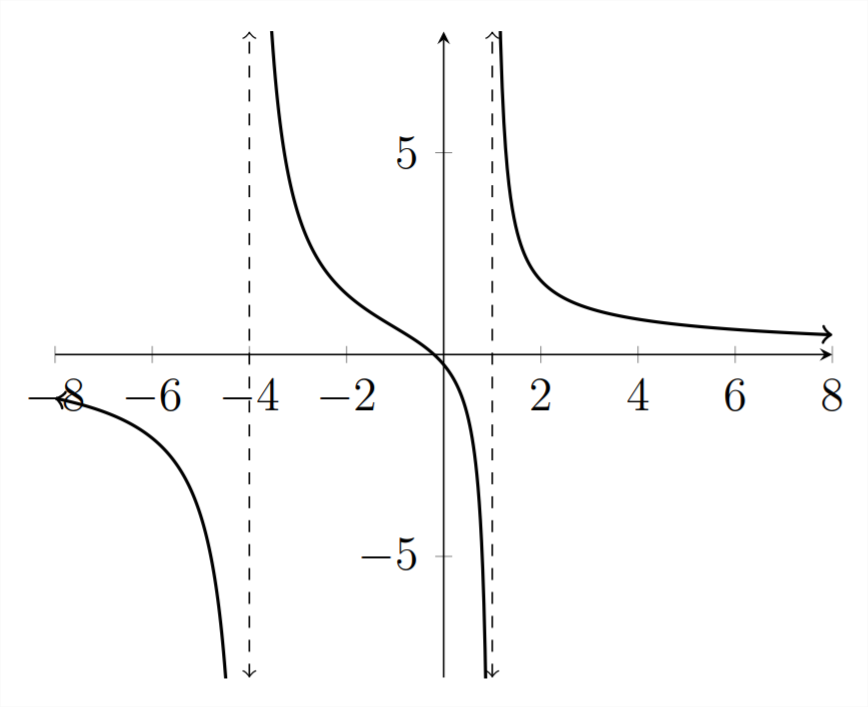
$clipboard_e74857b29ddc7c11e98c94557a0591108.png$

$5 x+1=0$
$5 x=-1$
$x=-0.2=-\frac{1}{5}$
Asíntotas de Raíces
$x^{2}+3 x-4=0$
$(x+4)(x-1)=0$
$x=-4,1$

$clipboard_e9275738b798e4d03c9e36e3f3614bb96.png$
Si combinamos el análisis algebraico anterior con lo que vemos en la gráfica, entonces sabemos que los puntos de división importantes para la solución de esta desigualdad están en$x=-4,-0.2,1 .$ Los intervalos donde los$y$ valores son menores que cero son$x<-4$$\mathrm{OR}-0.2<x<1$

Ejemplo
$\frac{x^{2}+2 x-1}{x^{2}+7 x+5} \leq 0$
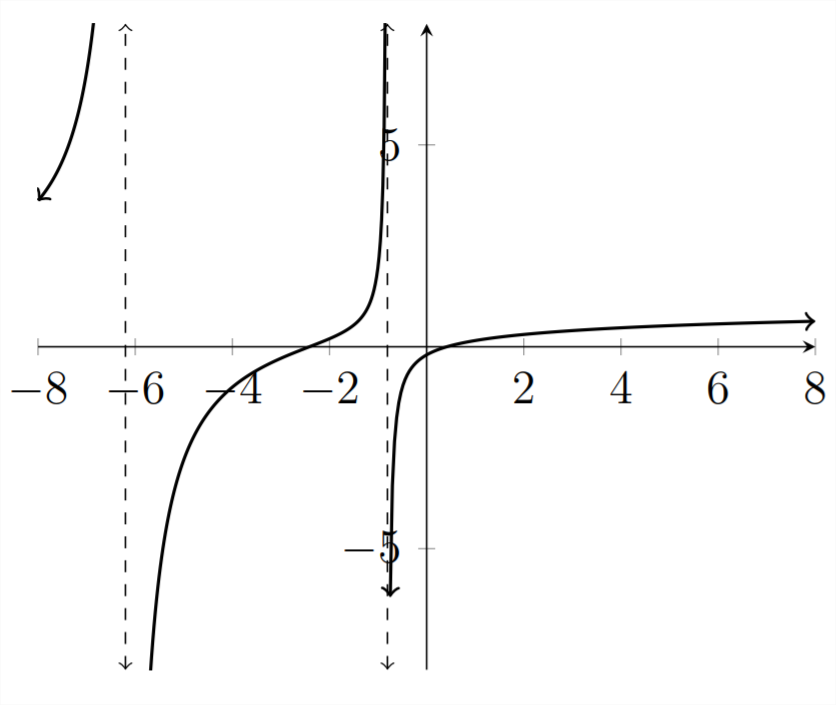
$clipboard_e643bedb58045d34286655db276af608a.png$
Raíces
\ [
\ begin {array} {l}
x^ {2} +2 x-1=0\\
x\ approx-2.414,0.414
\ end {array}
\]
Asíntotas
$x^{2}+7 x+5=0$
\ [
x\ approx-6.193, -0.807
\]
Podemos ver que los puntos de división importantes para la solución de la desigualdad son$x \approx-6.193,-2.414,-0.807,0.414 .$ Los intervalos donde$y$ los valores son menores o iguales a cero son $-6.193 \leq x \leq-2.414$O$-0.807 \leq x \leq 0.414$

Ejercicios 2.4
Resolver cada desigualdad.
1)$\quad \frac{x+4}{x^{2}-8 x+12}>0$
2)$\quad \frac{2 x+3}{x^{2}-2 x-35}<0$
3)$\quad \frac{x^{2}-5 x-14}{x^{2}+3 x-10}<0$
4)$\quad \frac{2 x^{2}-x-3}{x^{2}+10 x+16}>0$
5)$\quad \frac{3 x+2}{x^{2}+x-5}<0$
6)$\quad \frac{x^{2}+2 x+5}{x^{2}-3 x-7}>0$
7)$\quad \frac{x^{3}+9}{x^{2}+x-1}>0$
8)$\quad \frac{x^{3}+9}{x^{2}+x+1}>0$

Resolver cada desigualdad.
9)$\quad \frac{x^{2}-2 x-9}{3 x+11}>0$
10)$\quad \frac{x^{2}+4 x+3}{2 x+1}<0$
11)$\quad \frac{x^{2}+x-5}{x^{2}-x-6}>0$
12)$\quad \frac{x^{3}+2}{x^{2}-2}>0$
13)$\quad \frac{x^{2}+2 x-7}{x^{2}+3 x-6}<0$
14)$\quad \frac{2 x-x^{2}}{x^{2}-4 x+6}<0$
15)$\quad \frac{x^{2}-7}{x^{2}+5 x-1}<0$
16)$\quad \frac{x-5}{3 x^{2}-2 x-3}>0$