2.6: Polinomio División Larga

Última actualización
Guardar como PDF

Page ID: 111896

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

La división polinómica larga tiene muchas similitudes con la división larga numérica, por lo que es importante que entendamos cómo y por qué la división numérica larga funciona de la manera que lo hace antes de discutir la división polinómica larga. Primero el ¿CÓMO?

Dado el problema numérico$87,462 \div 38$, el primer paso es determinar el valor positorio más alto en la respuesta.
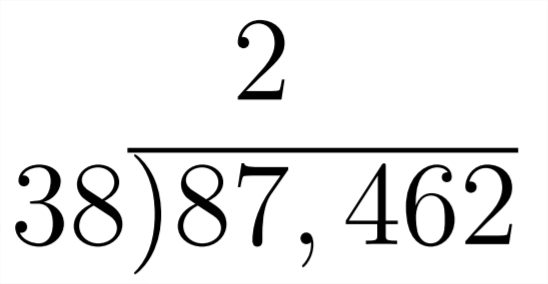
$clipboard_ed2ba040a3071430f7b59823a75925680.png$
A menudo el primer paso en la división numérica larga es decir “¿38 divide en$8 ? "$ “No”. “Hace 38 divide en$87 ? "$ “Sí”. Esto nos dice que el primer dígito en la respuesta será superior al 7 in$87,462,$ y consecuentemente estará en el lugar de miles. Una vez que sepamos que el primer dígito en la respuesta estará en el lugar de miles, la siguiente pregunta es “¿Cuántos miles?” Podemos determinar eso$2 *$$38=76$ pero$3 * 38=114$ (demasiado grande), así sabemos que el primer dígito en la respuesta será$2 .$ Luego restamos, incluimos el 4 y examinamos lo que queda para continuar.
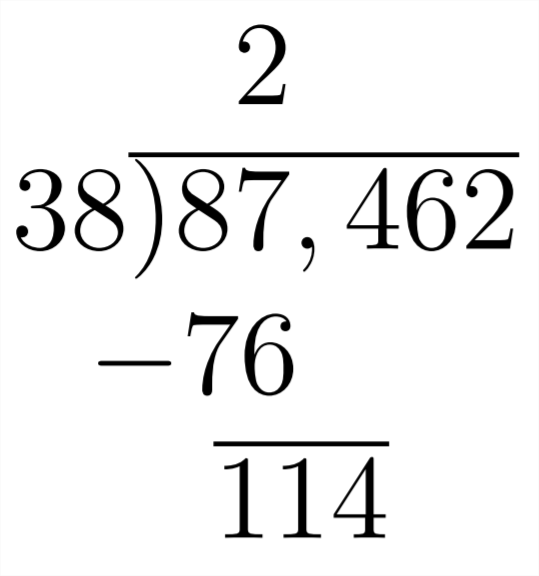
$clipboard_e6b232f274d05283aec148c5d3d9f1e89.png$
Aquí, vemos eso$114 \div 38=3$, así sabemos que el siguiente dígito en la respuesta será 3
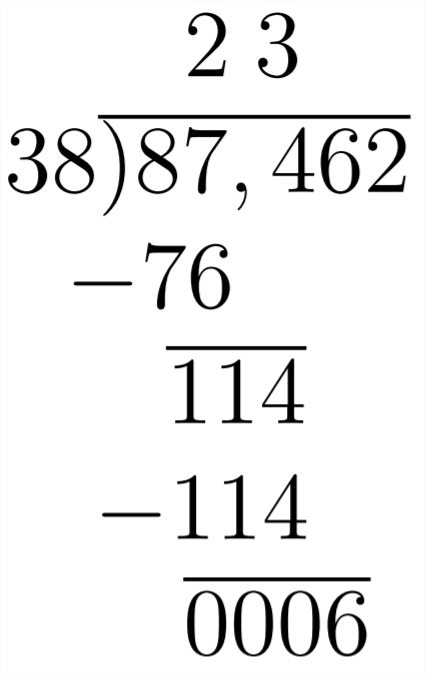
$clipboard_ecd4d4dabc0b1d7619e9f810ee7ce4ba7.png$
Después de incluir el$6,$ podemos ver que 38 no divide de manera uniforme en$6,$ así que ponemos un cero como el siguiente dígito en nuestro responder y proceder:

$clipboard_e4b25d2a075dea6e8eea5aaea5560f3c2.png$
Ahora que hemos incluido todos los dígitos de nuestro número original$87,462,$ el último paso es dividir 38 en$62 .$ Esto va una vez con 24 sobrantes.

Entonces, ahora tenemos la solución al problema original$87,462 \div 38=2,301 \mathrm{R} 24$ o ¿
$2,301 \frac{24}{38}$
El POR QUÉ? del algoritmo de división larga está algo oculto por el ¿CÓMO? En el primer paso, estamos determinando qué valor posicionar contendrá el primer dígito de nuestra respuesta. Cuando determinemos que 38 sí se divide en$87,$ esto indica que el primer dígito en nuestra respuesta será el lugar de miles. Dividir 38 en 87 nos dice cuántos miles habrá. Luego restamos:
\ [
\ begin {array} {r}
87.462\\
-76,000\
\ hline
11,462
\ end {array}
\]

Ahora tenemos que determinar cuántas veces 38 se dividirá en$11,462 .$ Decidimos$300 * 38=11,400,$ luego restamos para ver cuánto queda:
\ [
\ begin {array} {r}
11,462\\
-11,400\
\ hline
00,062
\ end { array}
\]
Podemos ver que no vamos a necesitar decenas en nuestra respuesta, y que 38 divide en 62 una vez con 24 sobrantes, así la respuesta es 2 miles, 3 cientos, no decenas, 1 y un resto de$24 .$ Para comprobar la respuesta, multiplicamos$38 * 2301$ y sumamos 24:
\ [
\ begin {array} {c}
2.301\\
\ veces 38\
\\ hline 18408\\
6903\
\ hline 87438\\
+24\
\ hline 87462
\ end {array}
\]
Polinomio largo la división funciona de la misma manera que lo hace la división numérica larga. Ante un problema$A \div B$, el objetivo es encontrar un cociente$Q$ y resto para$R$ que$A=B * Q+R$
veamos esto con el ejemplo$2 x^{4}+7 x^{3}+4 x^{2}-2 x-1 \div x^{2}+3 x+1$ o:
\ [
\ frac {2 x^ {4} +7 x^ {3} +4 x^ {2} -2 x-1} {x^ {2} +3 x+1}
\]
Entonces, estamos buscando responder a la pregunta:
\ [
\ begin {array} {cccccc}
A & = & B & * & Q & +R\\
2 x^ {4} +7 x^ {3} +4 x^ {2} -2 x-1 & = &\ left (x^ {2} +3 x+1\ right) & * & (? +? +?) & +?
\ end {array}
\]
Si queremos mulitply$x^{2}+3 x+1$ veces algo y terminar con$2 x^{4}+7 x^{3}+$$4 x^{2}-2 x-1,$ entonces lo que multiplicamos por va a tener que empezar$2 x^{2},$ porque
\ [
x^ {2} * 2 x^ {2} =2 x^ {4}
\]

Ahora estamos trabajando con esto:
\ [
\ begin {array} {cccc}
A & = & B & * & Q & +R\\
2 x^ {4} +7 x^ {3} +4 x^ {2} -2 x-1 & = &\ left (x^ {2} +3 x+1\ right) & * &\ left (2 x^ {2} +? +? \ derecho) & +?
\ end {array}
\]
Pero el$2 x^{2}$ no solo se multiplica por el$x^{2}$, también se multiplicará por el$3 x$ y el$1 .$ Así que ahora tenemos:
\ [
\ begin {array} {ccccc}
A & = & B & * & amp; Q & +R\\
2 x^ {4} +7 x^ {3} +4 x^ {2} -2 x-1 & = &\ izquierda (x^ {2} +3 x+1\ derecha) & * &\ izquierda (2 x^ {2} +? +? \ derecho) & +? \\
& & =2 x^ {4} +6 x^ {3} +2 x^ {2} +? ? ? ? ?
\ end {array}
\]

El tema que esto plantea es que la siguiente multiplicación$\left(? * x^{2}+? * 3 x+? * 1\right)$ necesita sumar sólo$1 x^{3}$ a nuestra respuesta, porque necesitamos$7 x^{3}$ y ya tenemos$6 x^{3}$ de la multiplicación anterior. Eso significa que vamos a querer multiplicar siguiente por
$1 x:$
\ [
\ begin {aligned}
A &=\ quad B\ quad *\ quad Q\ quad+R\\
2 x^ {4} +7 x^ {3} +4 x^ {2} -2 x-1 &=\ left (x^ {2} +3 x+1\ right) *\ left (2 x^ {2} +1 x+? \ derecho) +? \\
&=2 x^ {4} +6 x^ {3} +2 x^ {2}\\
&=\ quad 1 x^ {3} +3 x^ {2} +x\\
&=2 x^ {4} +7 x^ {3} +5 x^ {2} +1 x+? ? ?
\ end {aligned}
\]
En la siguiente ronda de multiplicación, vamos a querer$5 x^{2}$ bajar a$4 x^{2},$ así que tendremos que multiplicar por -1

\ [
\ comenzar {alineado}
A &=\ quad B\ cuádruple *\ cuádruple Q\ cuatrio+R\\
2 x^ {4} +7 x^ {3} +4 x^ {2} -2 x-1 &=\ izquierda (x^ {2} +3 x+1\ derecha) *\ izquierda (2 x^ {2} +1 x-1\ derecha) +0\\
&=2 x^ {4} +6 x^ {3} +2 x^ {2}\\
&=\ quad 1 x^ {3} +3 x^ {2} +x\\
& amp; =\ quad\ quad-1 x^ {2} -3 x-1\\
&=2 x^ {4} +7 x^ {3} +5 x^ {2} -2 x-1
\ end {alineado}
\]
Ahora también sabemos que el resto es cero, porque$x^{2}+3 x+1$ divide uniformemente en$2 x^{4}+7 x^{3}+4 x^{2}-2 x-1$ y así:
\ [
2 x^ {4} +7 x^ {3} +4 x^ {2} - 2 x-1=\ left (x^ {2} +3 x+1\ right) *\ left (2 x^ {2} +1 x-1\ right)
\]
Este método hace que el razonamiento detrás de dividir polinomios algo más aparente que el proceso de división larga, pero es más engorroso. La forma en que generalmente se aborda la división polinómica larga es la siguiente:
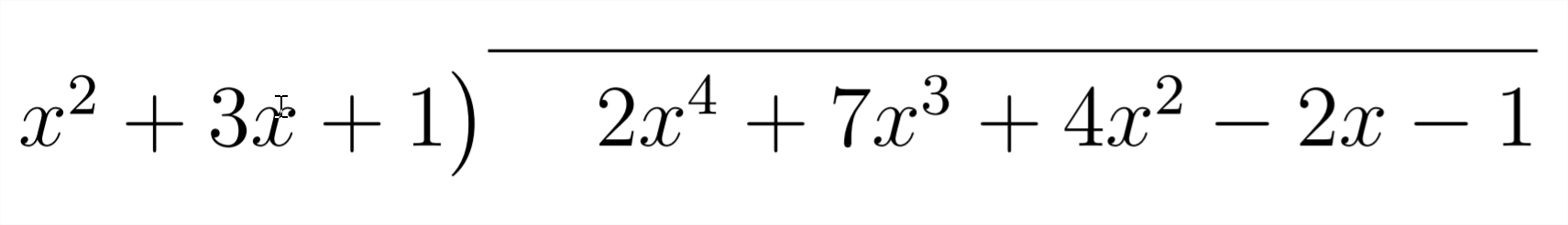
$clipboard_e6844c22fbb3ade41db7904a79287887f.png$
Entonces, tal como lo hicimos en el otro método, nos preguntamos “$x^{2}$Por qué debemos multiplicar para obtener$2 x^{4} ?^{\prime \prime}$ Respuesta:$^{\prime \prime} 2 x^{2 \prime \prime}$ Este es el primer término en nuestra respuesta:
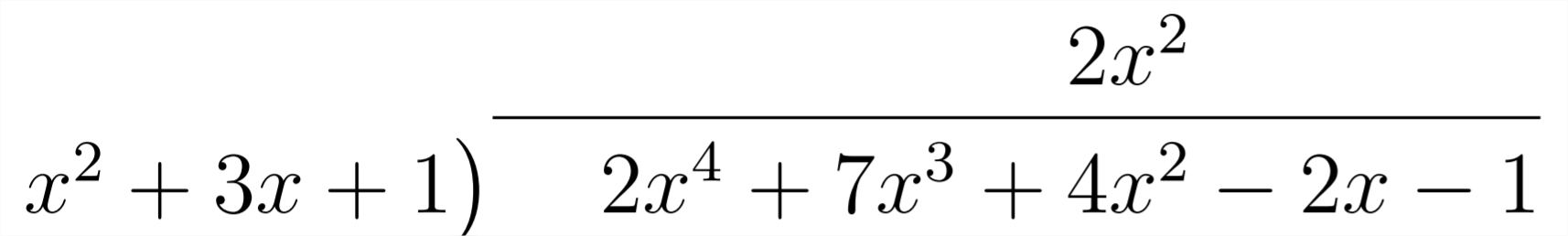
$clipboard_e7cbbe64f065d37ac2b0fcd9a75c2b610.png$
Entonces multiplicamos$2 x^{2}\left(x^{2}+3 x+1\right)$ y cambiamos todos los signos para ver con qué nos quedaremos:
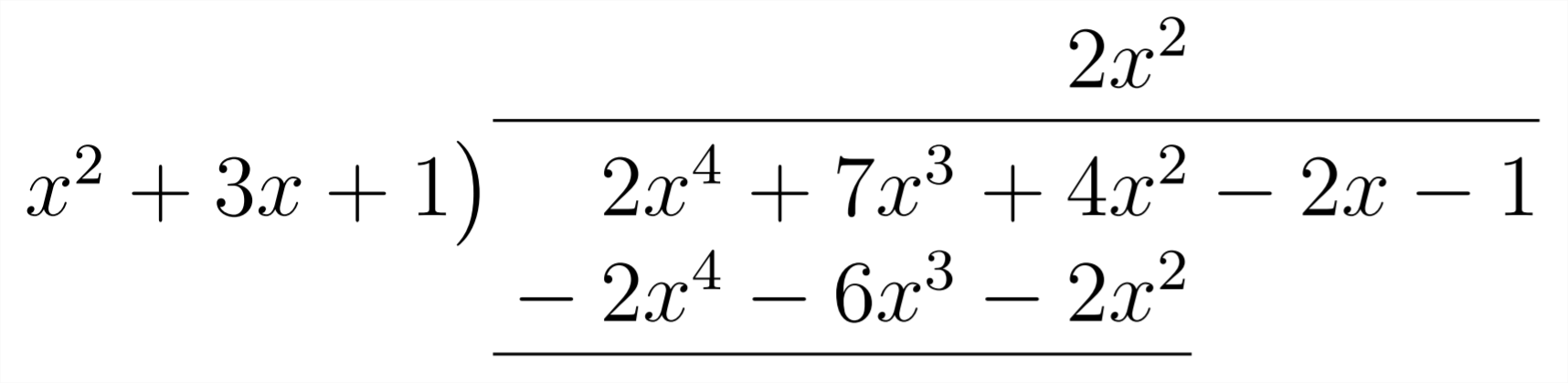
$clipboard_e925c204ba8a7317e34ef4d85629e7d7b.png$
Esto indica que$2 x^{4}$ tendremos los que necesitaremos en nuestra respuesta, así seis de los siete$x^{3}$ y dos de los cuatro$x^{2}$. Ahora necesitaremos lo$1 x^{3}$ siguiente:
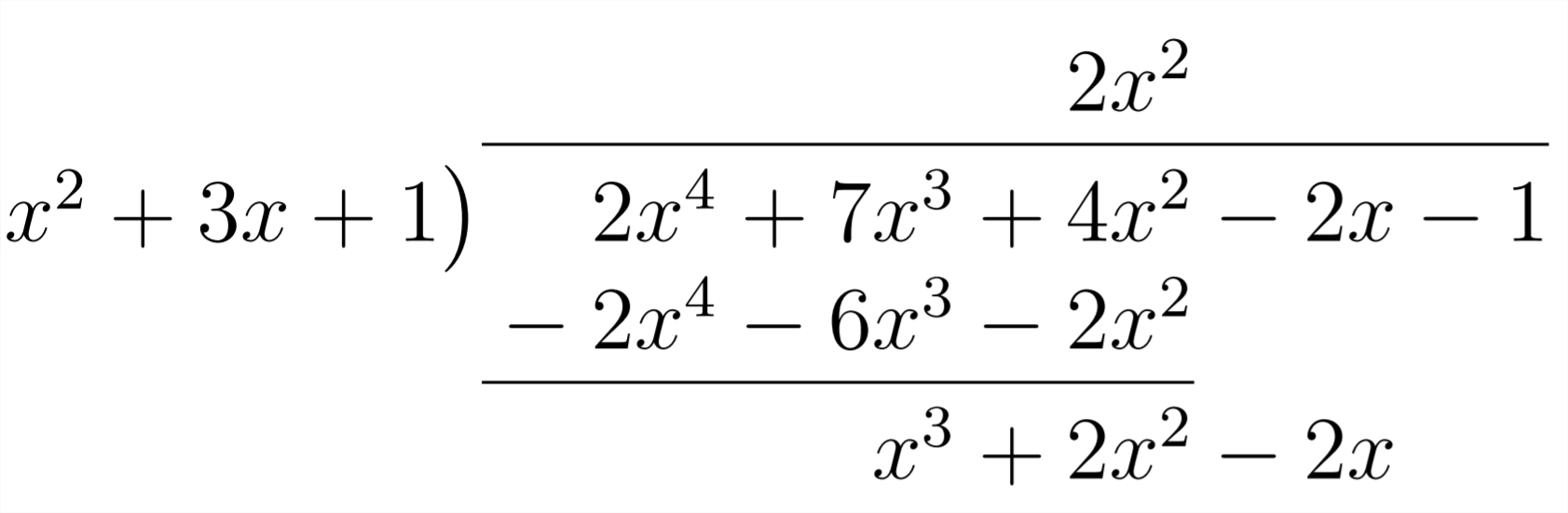
$clipboard_e7aa899f9db61c5cb4f625a6a817843c9.png$

Esto significa que tendremos que multiplicar por$1 x$:
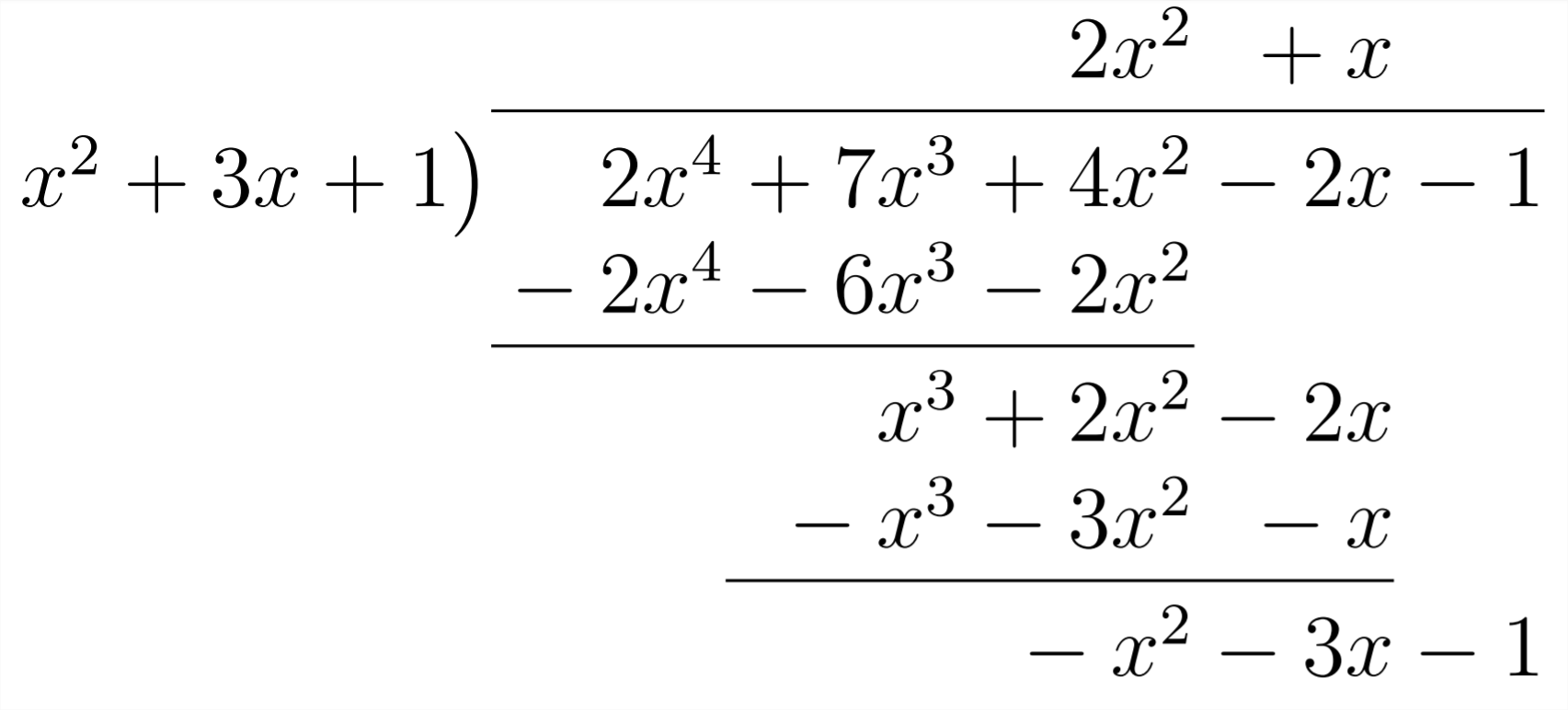
$clipboard_ed89447f91a5d341c3c631775e6768208.png$
Aquí, todavía tenemos que recoger a$-1 x^{2}$, lo que significa que nuestra próxima multiplicación será con -1:
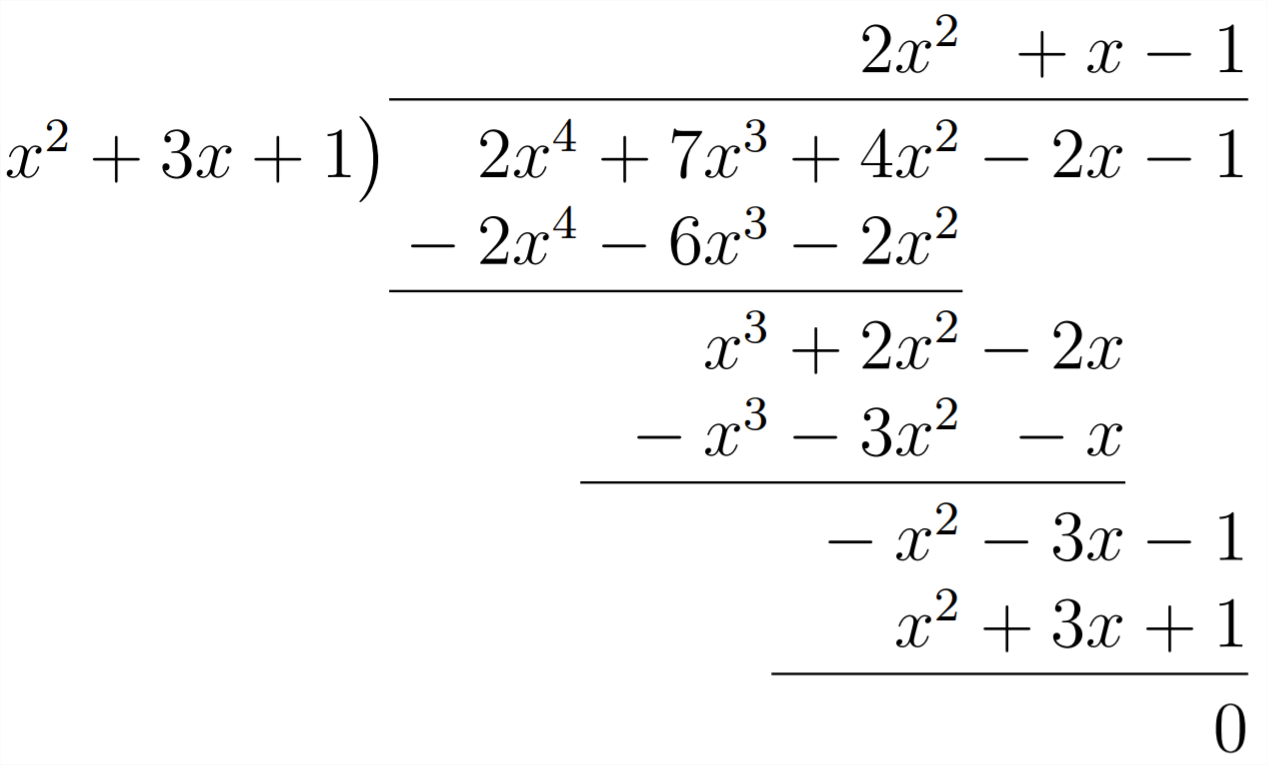
$clipboard_e88a85820281b3748939afbd248326c03.png$
Porque$x^{2}+3 x+1$ divide uniformemente en$2 x^{4}+7 x^{3}+4 x^{2}-2 x-1$ tenemos un cero resto. En el siguiente ejemplo habrá un resto distinto de cero:

Ejemplo
Dividir:
$\frac{3 x^{4}-8 x^{3}+19 x^{2}-15 x+10}{x^{2}-x+4}$

Primero, configuramos el problema:
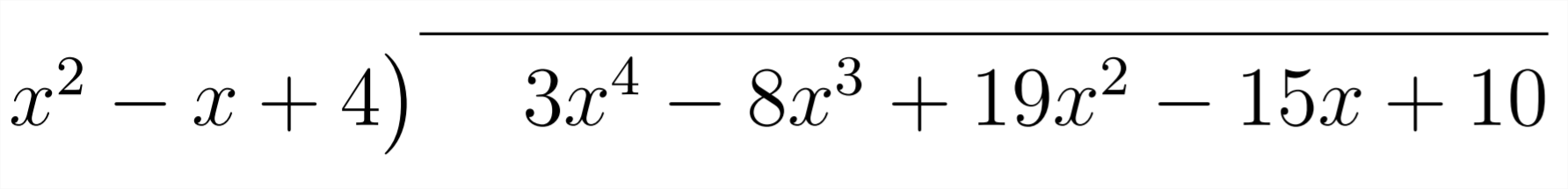
$clipboard_efbaabb96fffae5db68554aca4c5c8243.png$
Luego, nos preguntamos: “$x^{2}$Por qué necesitamos multiplicar para obtener$3 x^{4} ? "$ Respuesta:
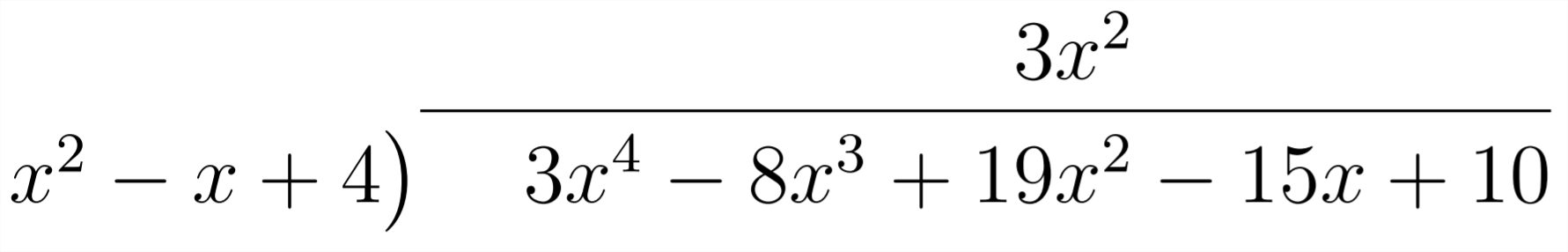
$clipboard_eb4da1474c2ccf5407726a4dd823488f4.png$
Entonces, multiplicamos, cambiamos signos (restamos) y combinamos términos como:
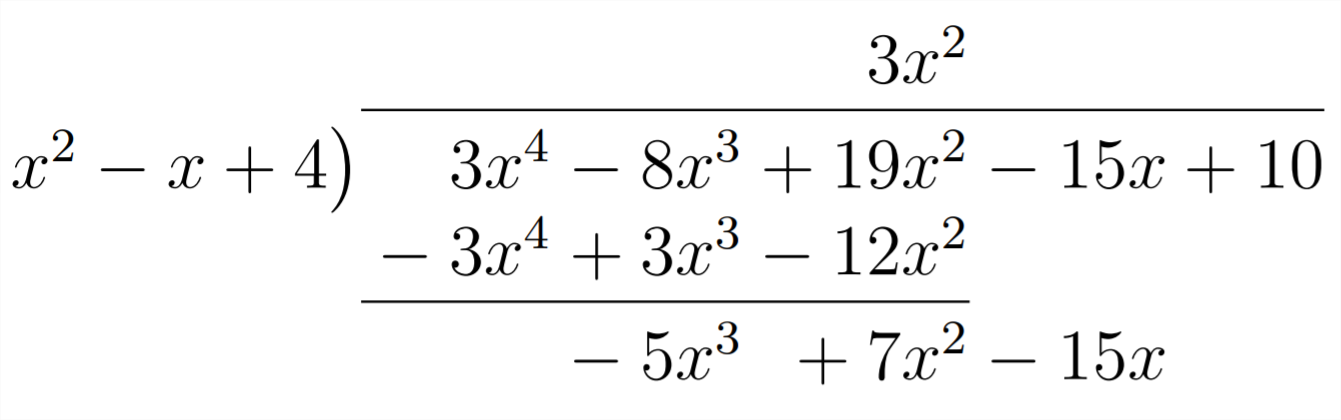
$clipboard_e67b5ec2c4ab9795adb03421c1ba2fa09.png$
Ahora tendremos que multiplicar por signos de$-5 x,$ cambio y combinar términos similares:
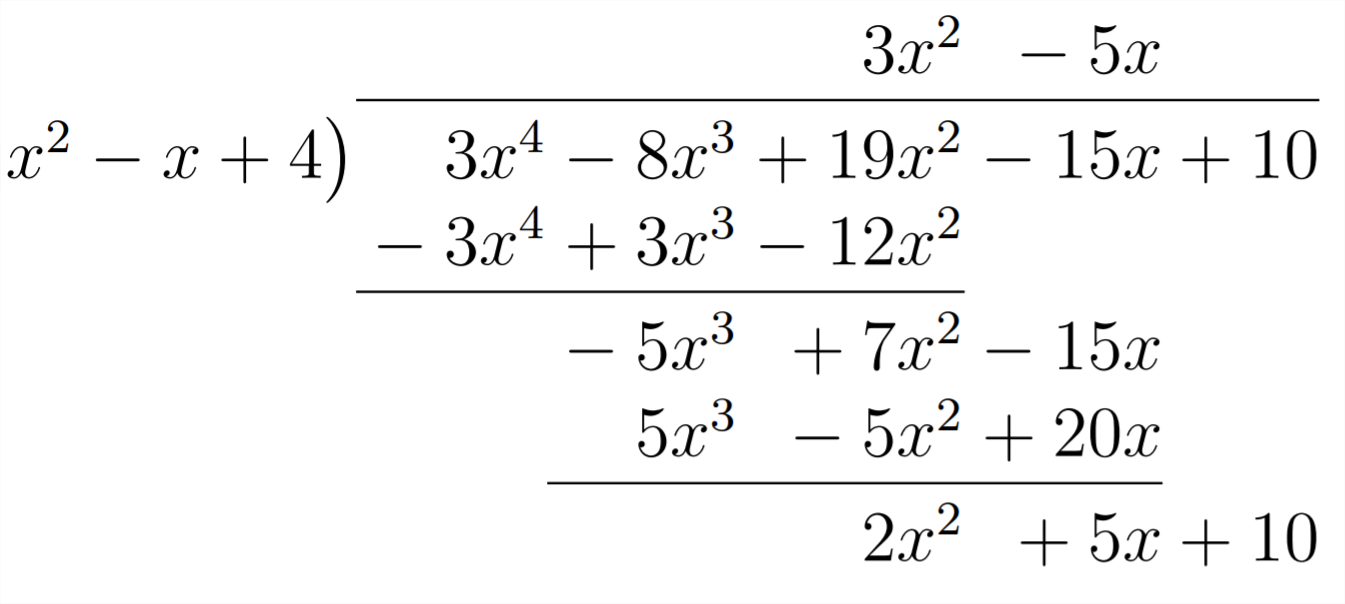
$clipboard_e02a4c3a1d2a6ac1f1f8e011f9e12f546.png$
Necesitamos$2 x^{2}$ así que necesitaremos multiplicar por 2, cambiar signos y combinar términos similares:
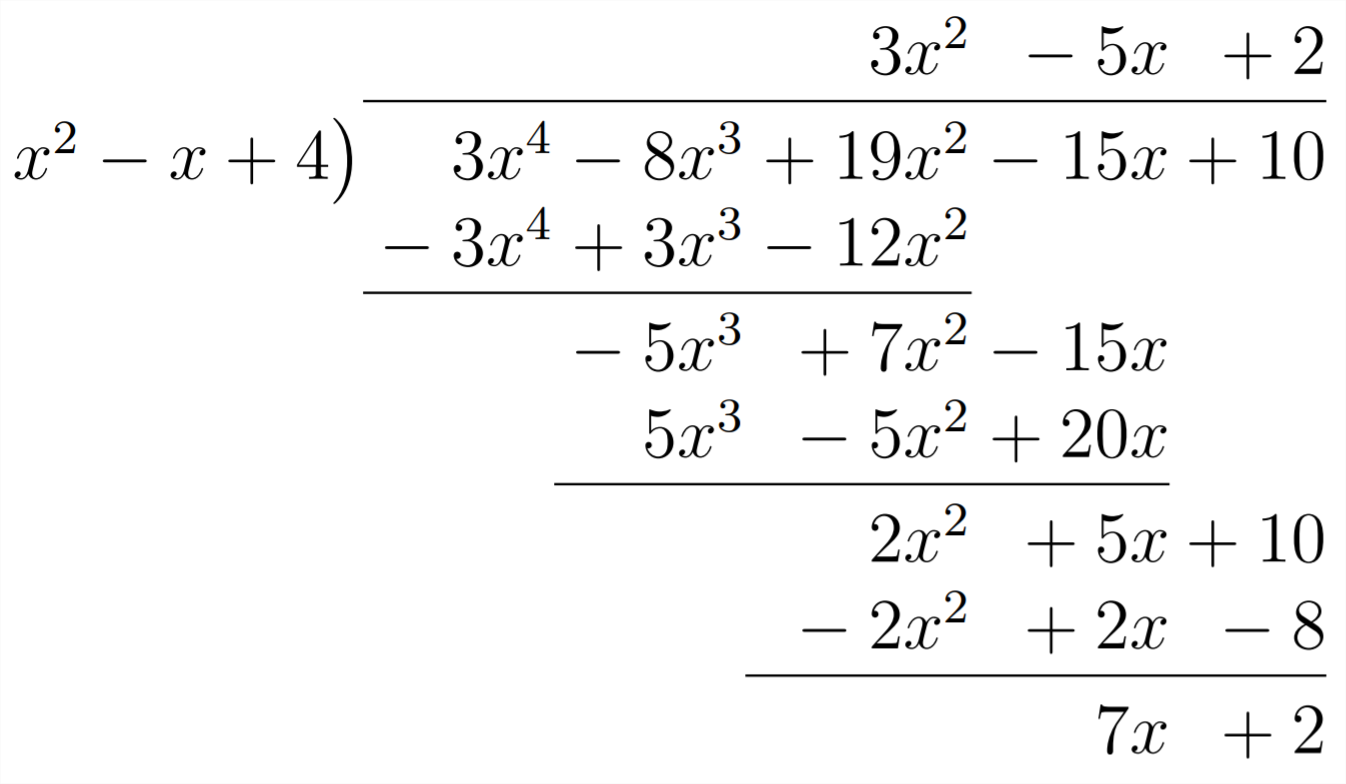
$clipboard_e89ea259b1b586107435786424a0225dc.png$

Debido a que no hay poder positivo de$x$ eso podemos multiplicar$x^{2}$ por para obtener$7 x,$ entonces este es nuestro resto:$7 x+2$
Así:
\ [
\ begin {array} {ccccc}
A & = & B & * & Q & + & R\\
3 x^ {4} -8 x^ { 3} +19 x^ {2} -15 x+10 & =\ izquierda (x^ {2} -x+4\ derecha) & *\ izquierda (3 x^ {2} -5 x+2\ derecha) & + (7 x+2)
\ final {matriz}
\]

Ejercicios 2.6
Encontrar el cociente en cada problema.
1)$\frac{y^{3}-4 y^{2}+6 y-4}{y-2}$
2)$\frac{x^{3}-5 x^{2}+x+15}{x-3}$
3)$\frac{x^{3}-4 x^{2}-3 x-10}{x^{2}+x+2}$
4)$\frac{2 x^{3}-3 x^{2}+7 x-3}{x^{2}-x+3}$
5)$\frac{x^{4}+2 x^{3}-x^{2}+x+6}{x+2}$
6)$\frac{x^{4}+x^{3}+5 x^{2}+3 x+6}{x^{2}+x-1}$
7)$\frac{2 z^{3}+5 z+8}{z+1}$
8)$\frac{x^{5}+3 x+2}{x^{3}+2 x+1}$
9)$\frac{x^{4}+2 x^{3}+4 x^{2}+3 x+2}{x^{2}+x+2}$
10)$\frac{2 x^{4}+3 x^{3}+3 x^{2}-5 x-3}{2 x^{2}-x-1}$
11)$\frac{2 y^{5}-3 y^{4}-y^{2}+y+4}{y^{2}+1}$
12)$\frac{3 x^{5}-4 x^{3}+3 x^{2}+12 x-10}{x^{2}+2 x-1}$
13)$\frac{5 x^{4}-3 x^{2}+2}{x^{2}-3 x+5}$
14)$\frac{3 y^{3}-4 y^{2}-3}{y^{2}+5 y+2}$