2.7: División Sintética

Última actualización
Guardar como PDF

Page ID: 111866

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

El proceso para la división polinómica larga (como el proceso para la división numérica larga) se ha separado un poco de sus bases lógicas para un método más eficiente para llegar a una respuesta. Para tipos particulares de división larga polinomial, incluso podemos llevar esta abstracción un paso más allá. La división sintética es un atajo útil para problemas polinomiales de división larga en los que estamos dividiendo por un polinomio lineal. Esto quiere decir que el poder más alto de$x$ nosotros estamos dividiendo por tiene que ser$x^{1}$. Esto limita la utilidad de la División Sintética, pero nos va a servir bien para ciertos fines. Examinemos de dónde provienen los coeficientes en nuestra respuesta cuando dividimos por un polinomio lineal:

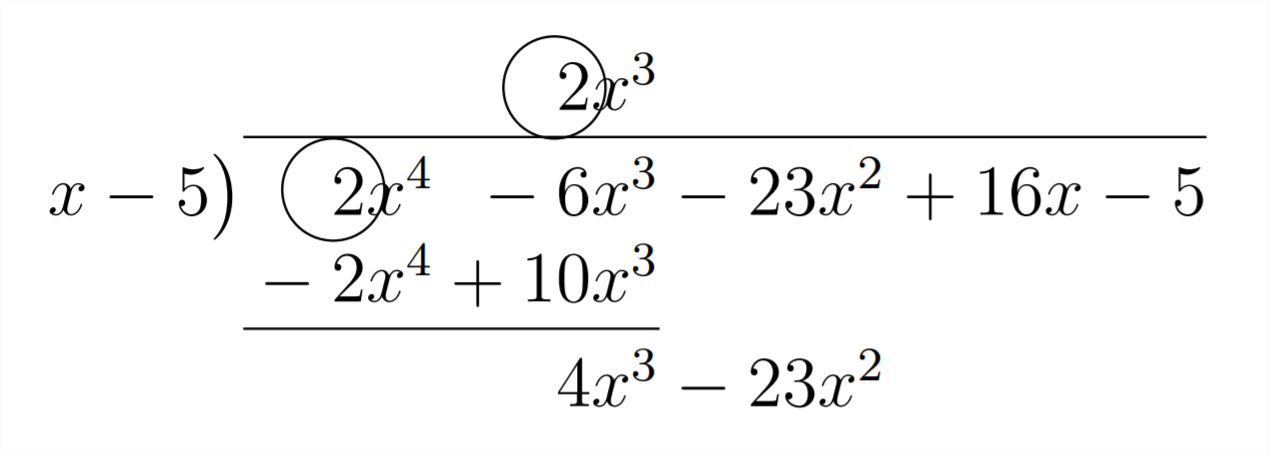
$clipboard_ea497b13197aab4a7a1489aaa8ae0b8b7.png$

Observe que el primer coeficiente en la respuesta es el mismo que el primer coeficiente en el polinomio en el que estamos dividiendo. Esto se debe a que estamos dividiendo por un polinomio en la forma$1 x^{1}-a .$ Esto también hace que el poder del primer término en la respuesta sea uno menos que el poder del polinomio en el que estamos dividiendo. Veamos de dónde provienen los coeficientes subsiguientes en la respuesta:

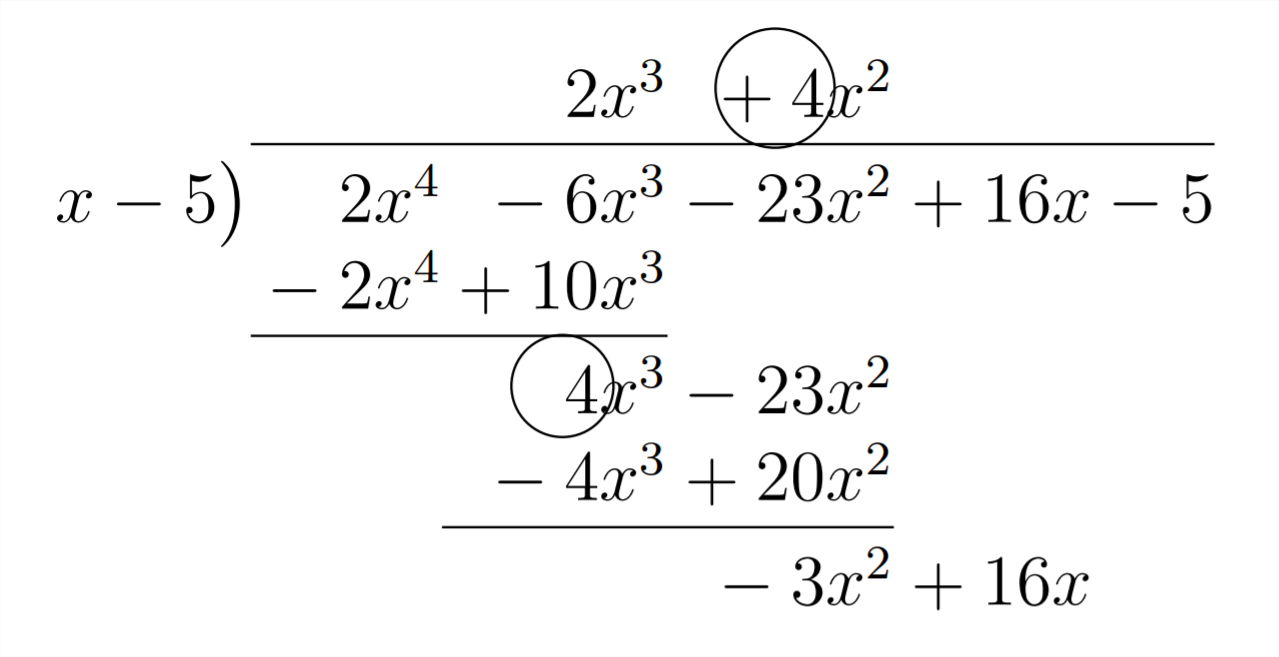
$clipboard_ef3dc7bc9ca9a34052ed5abead9864b63.png$

El siguiente coeficiente en la respuesta (4) proviene de la combinación del -6 y el$+10 .$ El +10 vino de multiplicar el 2 en la respuesta por el 5 en el divisor$x-5 .$ El siguiente coeficiente en la respuesta será el$-3,$ que viene de multiplicar el 4 (en la respuesta) por el 5 (en el divisor) y combinándolo con el -23 en el polinomio estamos dividiendo en:

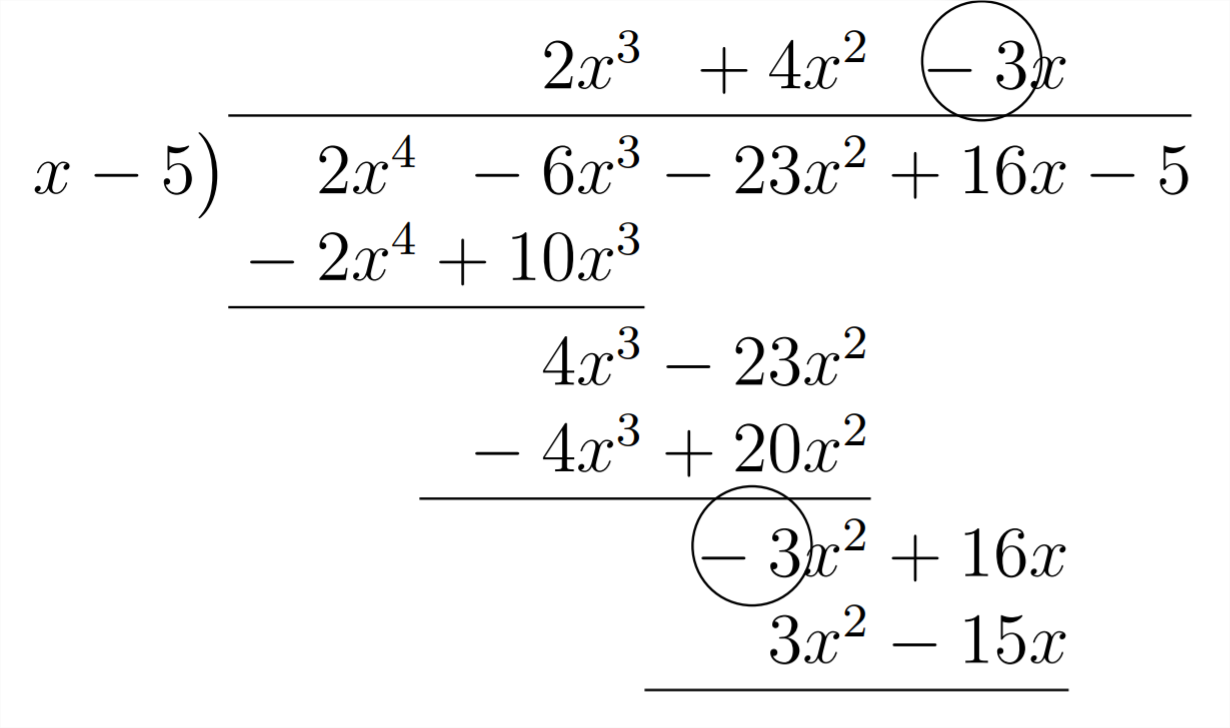
$clipboard_e22faa11d3b3df6b557d05807793aa2e5.png$

La última parte de nuestra respuesta vendrá de multiplicar el -3 en los tiempos de respuesta el 5 en el divisor (haciendo -15) y combinando esto con el +16 en el polinomio que estamos dividiendo en:

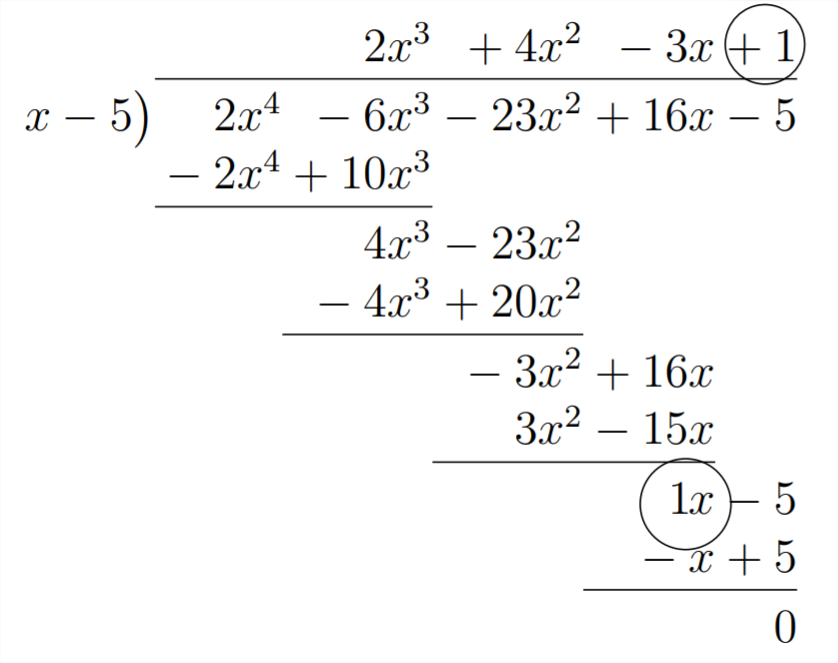
$clipboard_e7616163c53e4868697bb0295d3a04f1b.png$

El proceso de División Sintética utiliza estas relaciones como un atajo para encontrar la respuesta. La configuración para un problema de División Sintética se muestra a continuación:

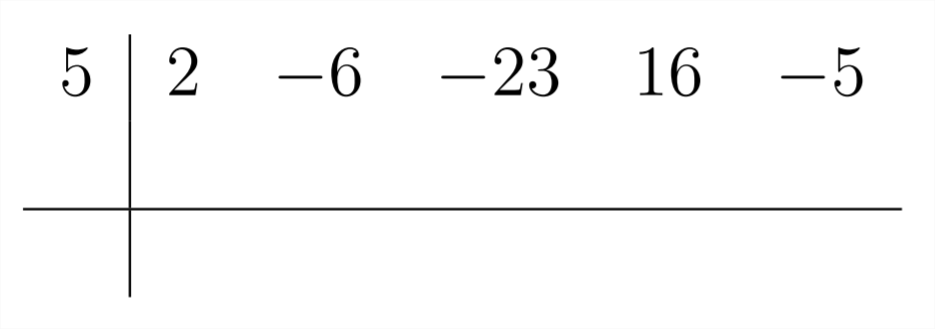
$clipboard_ea1255c9721dd7cb9a35d1d57f8269b62.png$

Esta configuración nos permite completar el problema de división$\frac{2 x^{4}-6 x^{3}-23 x^{2}+16 x-5}{x-5}.$
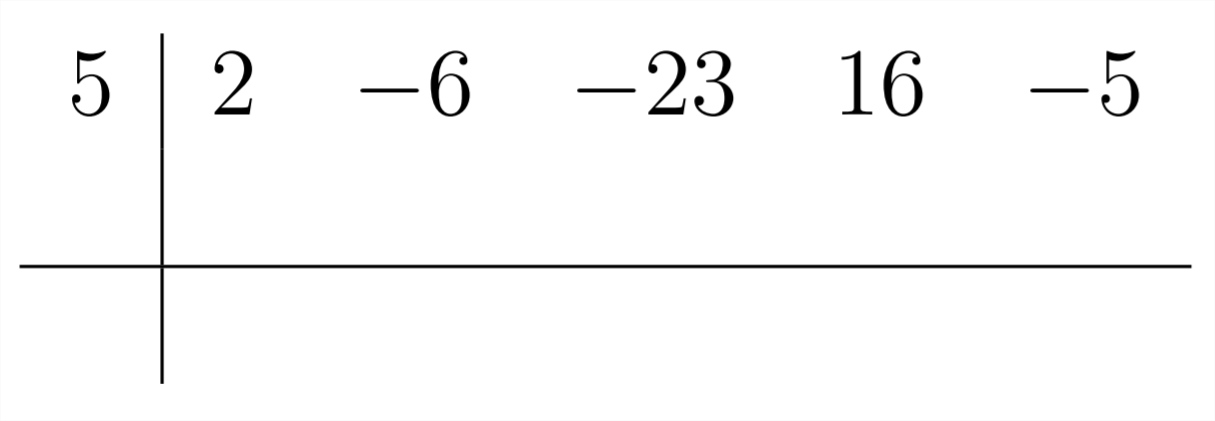
$clipboard_e8103490322a618427de0baf1456a0eb6.png$
El primer coeficiente en la respuesta es el mismo que el primer coeficiente en el polinomio en el que estamos dividiendo:
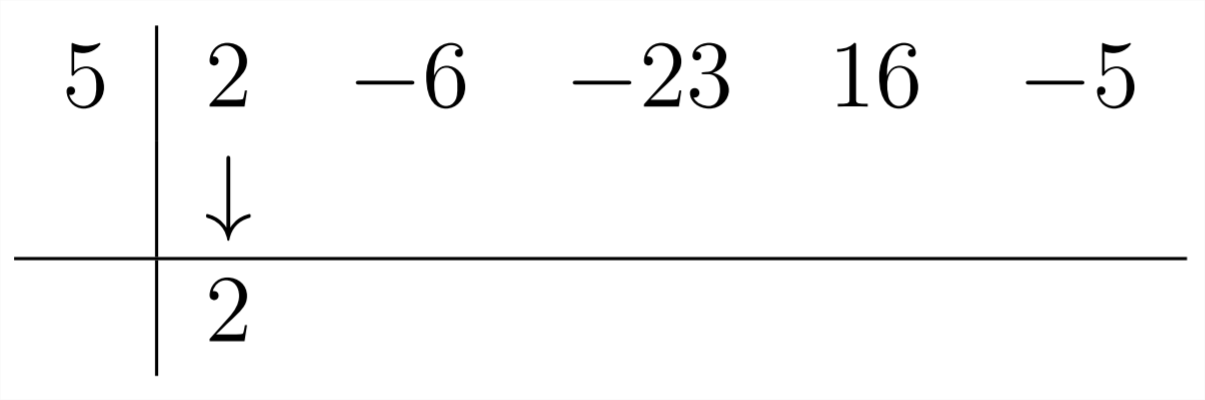
$clipboard_e808addf2e25f4f006c9e14c4632d3820.png$
Para obtener el siguiente coeficiente, multiplicamos el 2 por el 5 para obtener +10 y flll esto en debajo del -6:
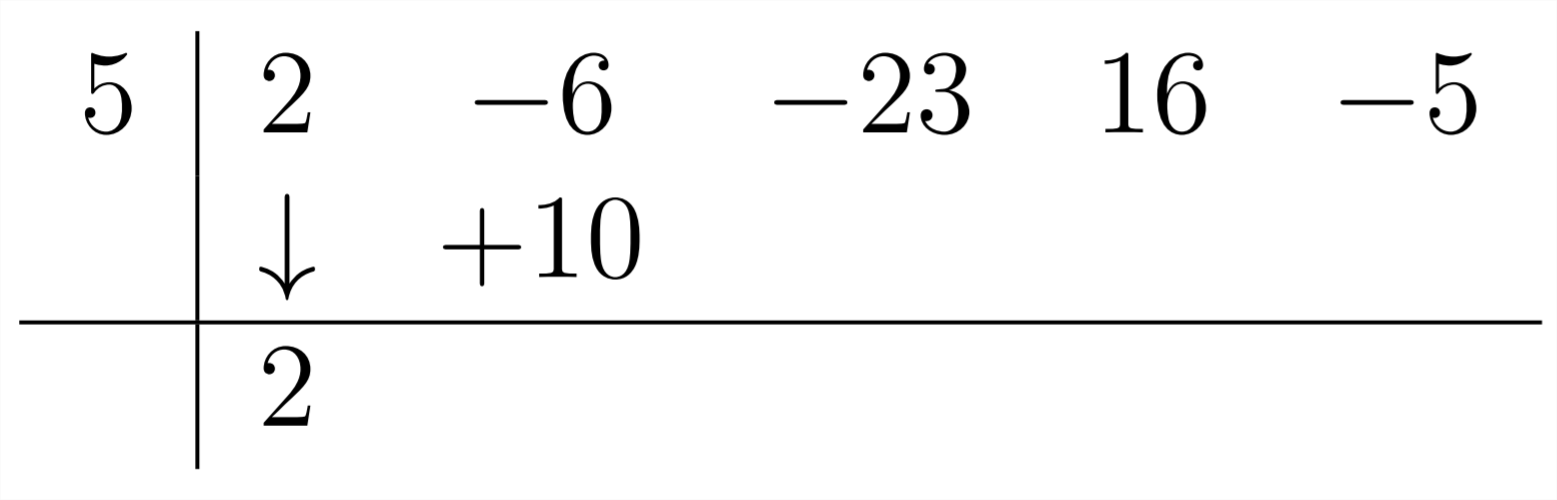
$clipboard_e58262a9b335ce0cbfa16a7aeac9d37f2.png$
Entonces,$-6+10=+4,$ cual es el siguiente coeficiente en la respuesta:
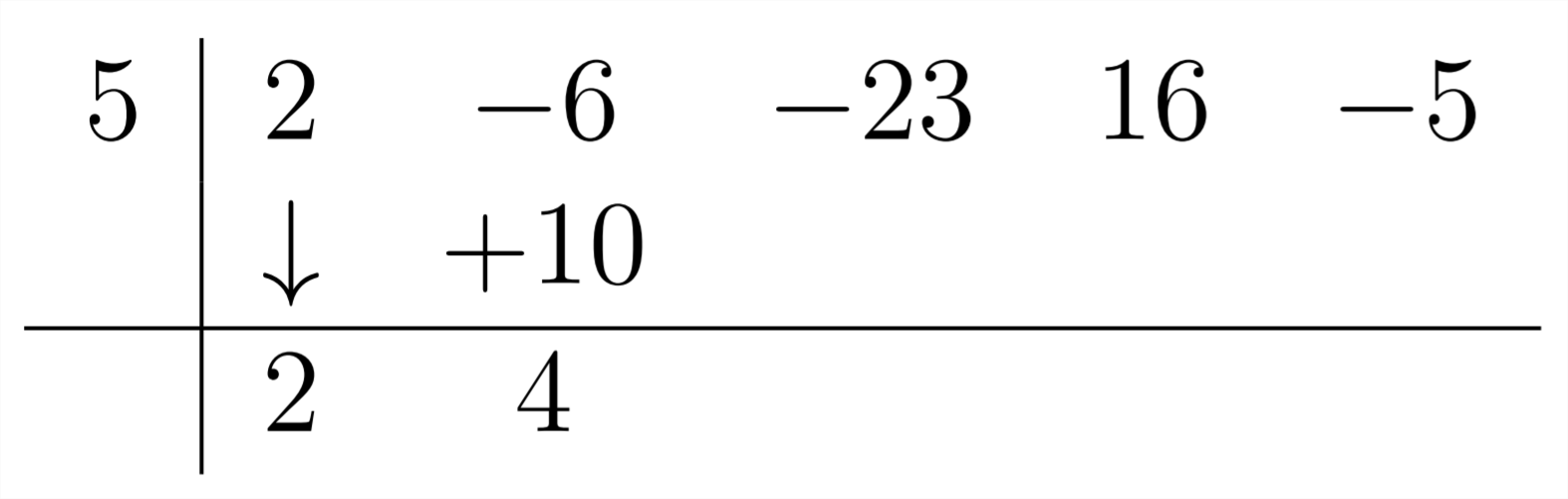
$clipboard_ec4659864ccbf9d590f340bc27793abb7.png$
Entonces, continuamos este proceso, multiplicando el 4 por el 5 para obtener 20 y combinando esto con el$-23:-23+20=-3:$
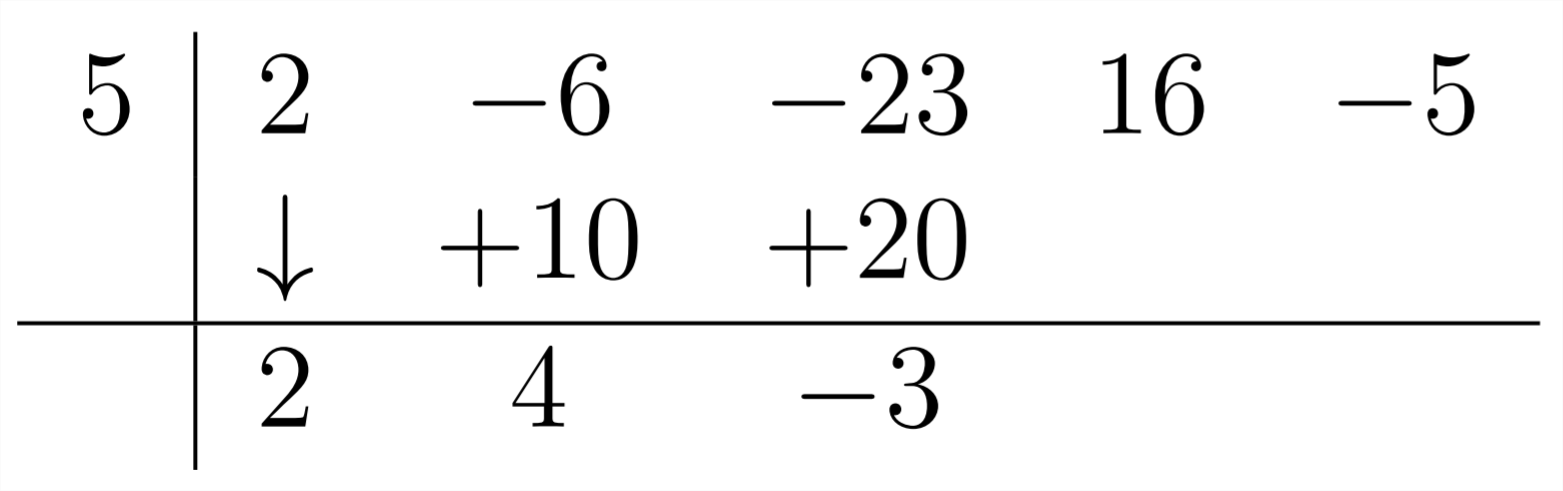
$clipboard_e029487a23774b110edec62b9f2142034.png$
A continuación, multiplica el -3 por el 5 y combina el -15 resultante con el 16:
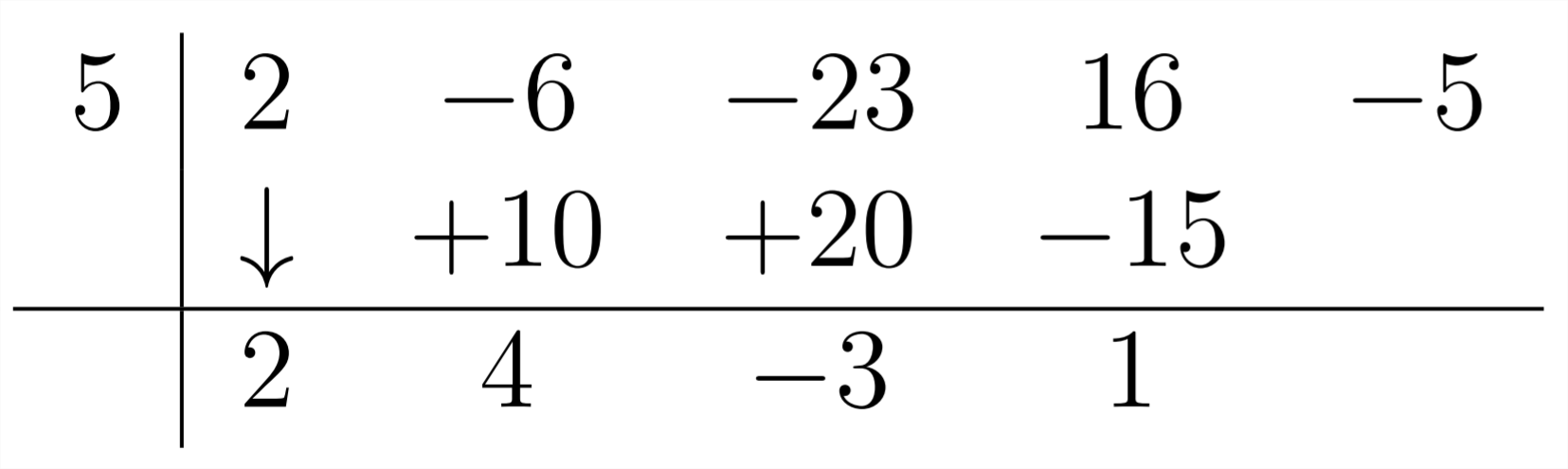
$clipboard_e76229205e52ee7e98258e6c72e1ef61a.png$
En el último paso, multiplica el 1 por el 5 y combina el resultado con el -5 en el problema para obtener cero:
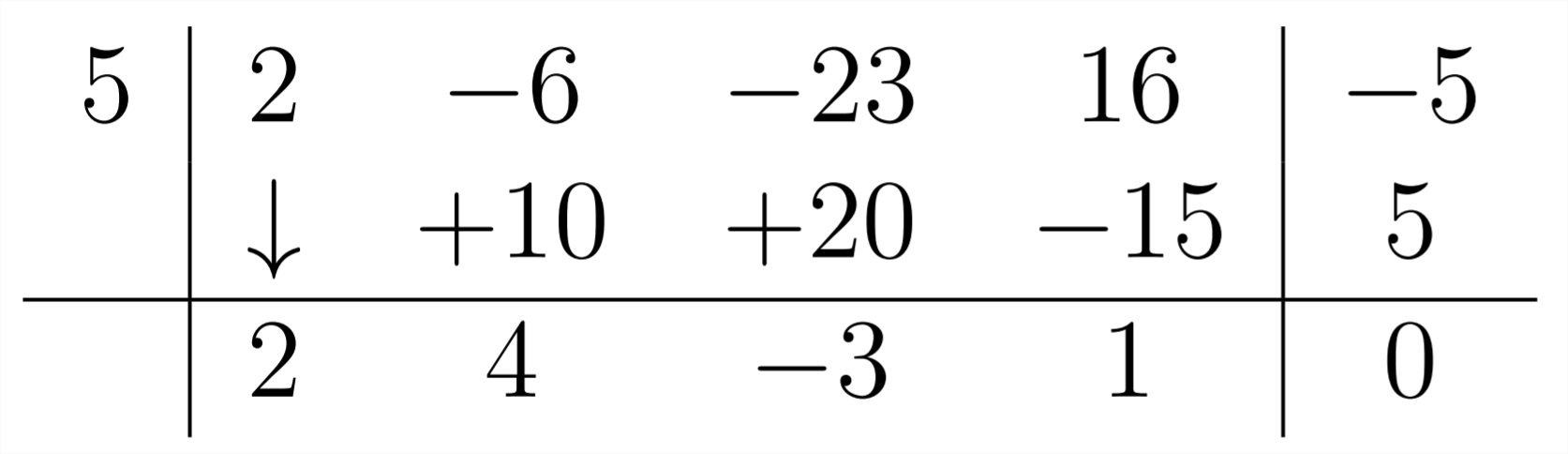
$clipboard_efad7ea830dd8c0cbfdf5d23644bf663f.png$
Este último coeficiente representa el resto -en este caso 0. Los otros números en la respuesta representan los coeficientes para las potencias de$x$ en la respuesta. En el extremo derecho está el resto, luego el$\left(x^{0}\right)$ término constante, luego el$\left(x^{1}\right)$ término lineal y así sucesivamente:
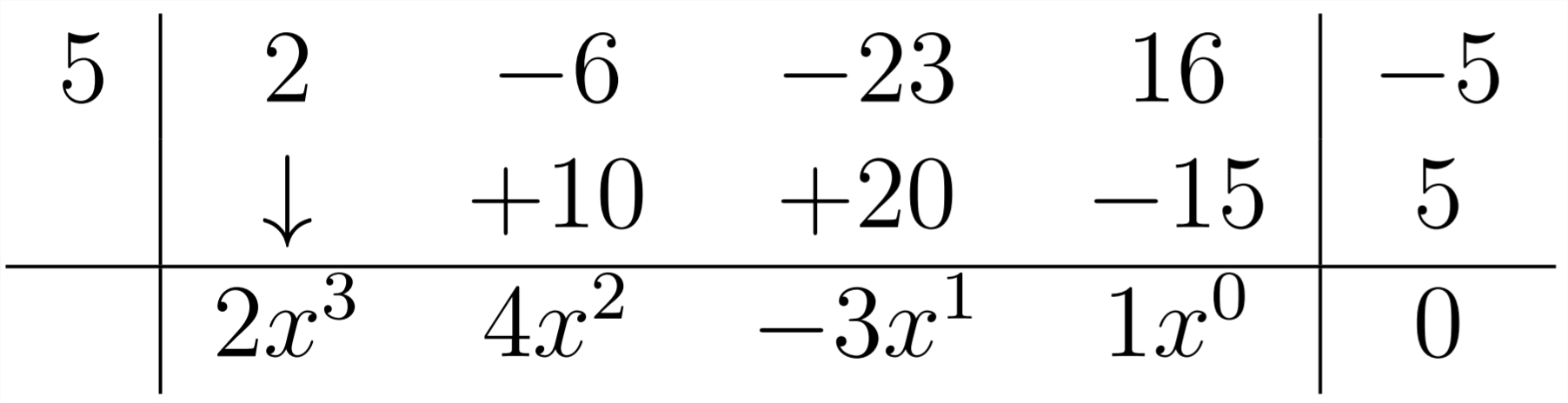
$clipboard_e9466b334e7b708dd1498444e292db198.png$
$\frac{2 x^{4}-6 x^{3}-23 x^{2}+16 x-5}{x-5}=2 x^{3}+4 x^{2}-3 x+1$
Veamos otro ejemplo:

Ejemplo
Use Sintético División a dividir:
$\frac{3 x^{3}+5 x^{2}-9 x+9}{x+3}$
ya que la División Sintética está establecida para dividir por$x-a$, si estamos dividiendo por$x+3$ tendremos que usar un -3 en la División Sintética:
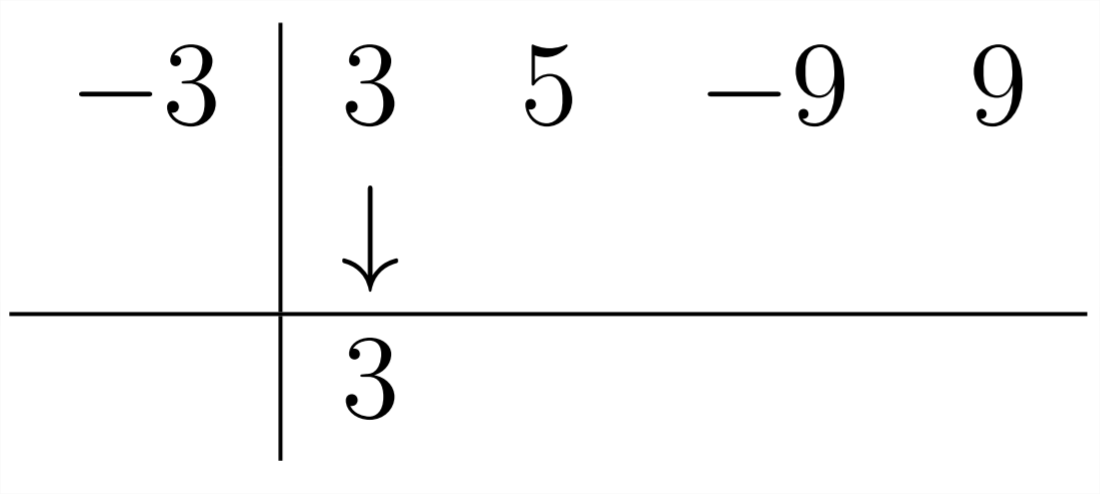
$clipboard_e41519fa4291dfe42e4f72a28d2b877ea.png$
Entonces,$3 *-3=-9$
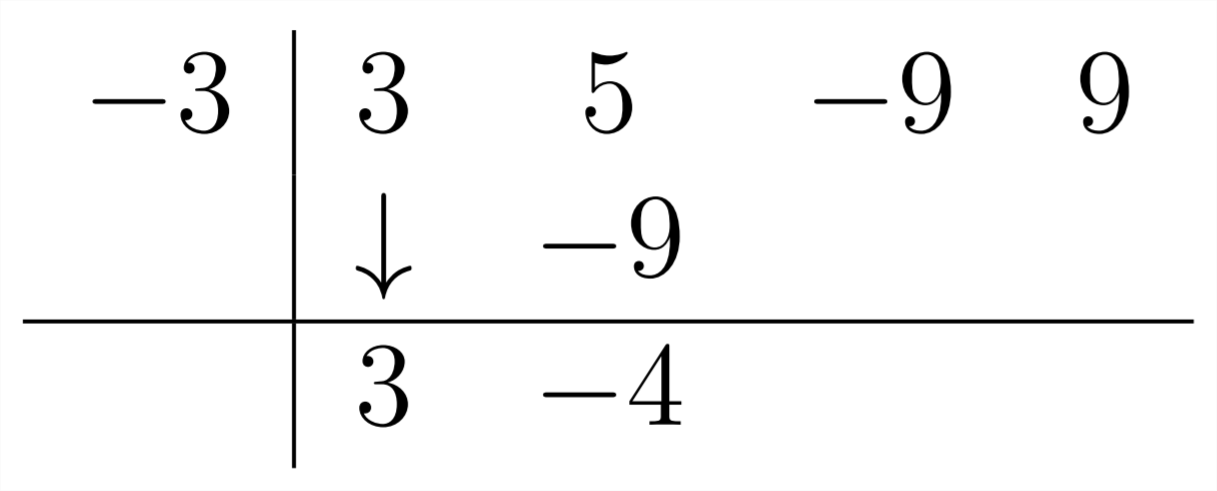
$clipboard_ee33767573b1a35fe9157d55d09f8f399.png$
Siguiente,$-4 *-3=+12$
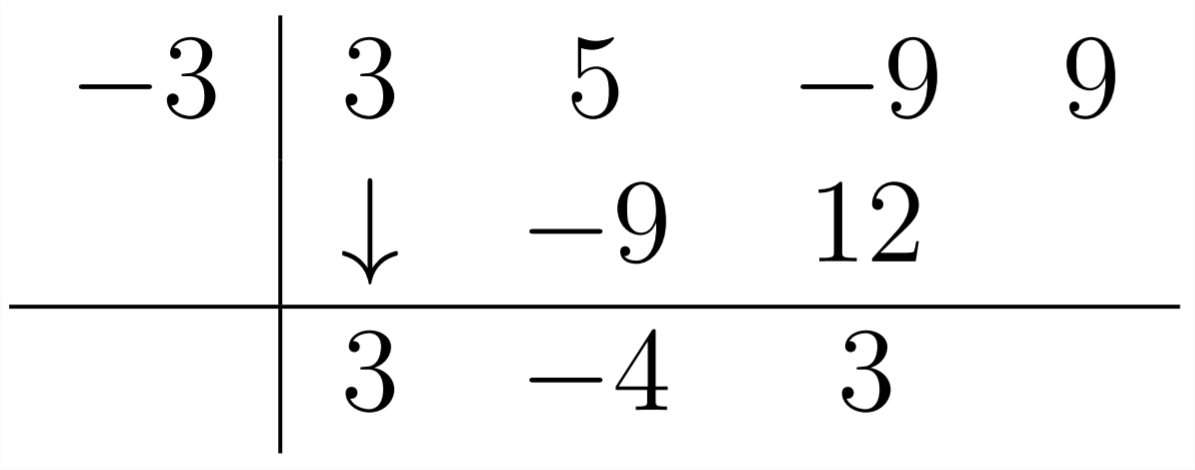
$clipboard_e8eb3f095ea9f7d050b78ee2ab8ca6f48.png$
Y este ejemplo también tiene un resto cero:
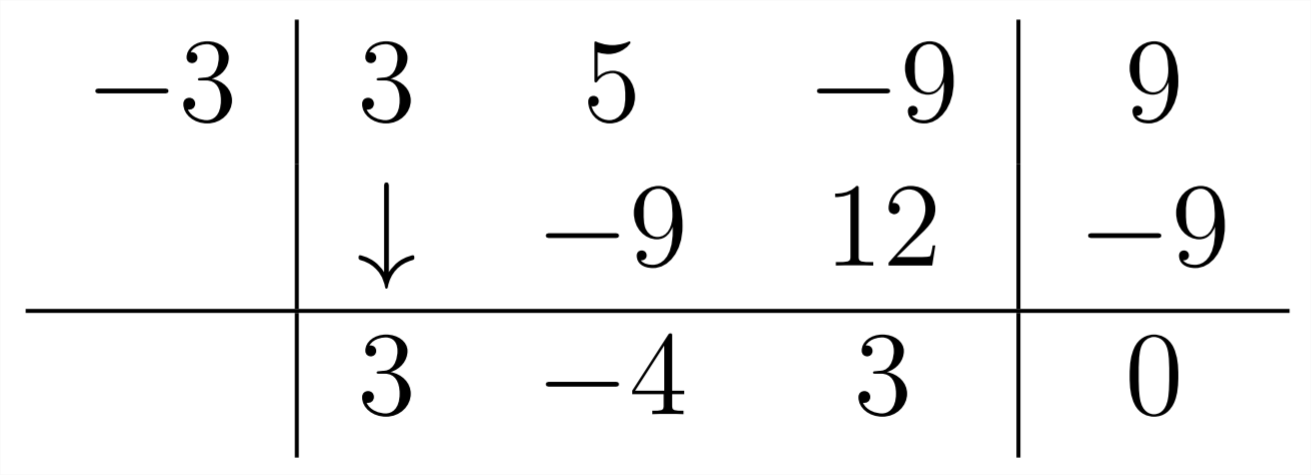
$clipboard_eb9339500ce4332f25792ad4b26f4aee9.png$
La respuesta aquí es$3 x^{2}-4 x+3$
\ [
\ frac {3 x^ {3} +5 x^ {2} -9 x+9} {x+3} =3 x^ {2} -4 x+3
\]
y
\ [
3 x^ {3} +5 x^ {2} -9 x+9 =( x+3)\ left (3 x^ {2} -4 x+3
\ right)\]
Veamos un ejemplo que es un poco diferente.

Ejemplo
Usar División Sintética para dividir: La división
$\frac{6 x^{4}+x^{3}+9 x^{2}+x-2}{2 x+1}$
sintética se configura para manejar problemas en los que estamos dividiendo por$1 x-a .$ Claramente, este no es el caso en este ejemplo, sin embargo podemos trabajar en torno a esto. Otra forma de ver la configuración de la división sintética es que usemos el número que es la solución a$x-a=0 .$ Cuando$x-5,$ dividimos por usamos
+5. Cuando estábamos dividiendo por$x+3$, usábamos$-3 .$ Entonces, si vamos a dividir por$2 x+1,$ usaremos$-\frac{1}{2}$ en la División Sintética:
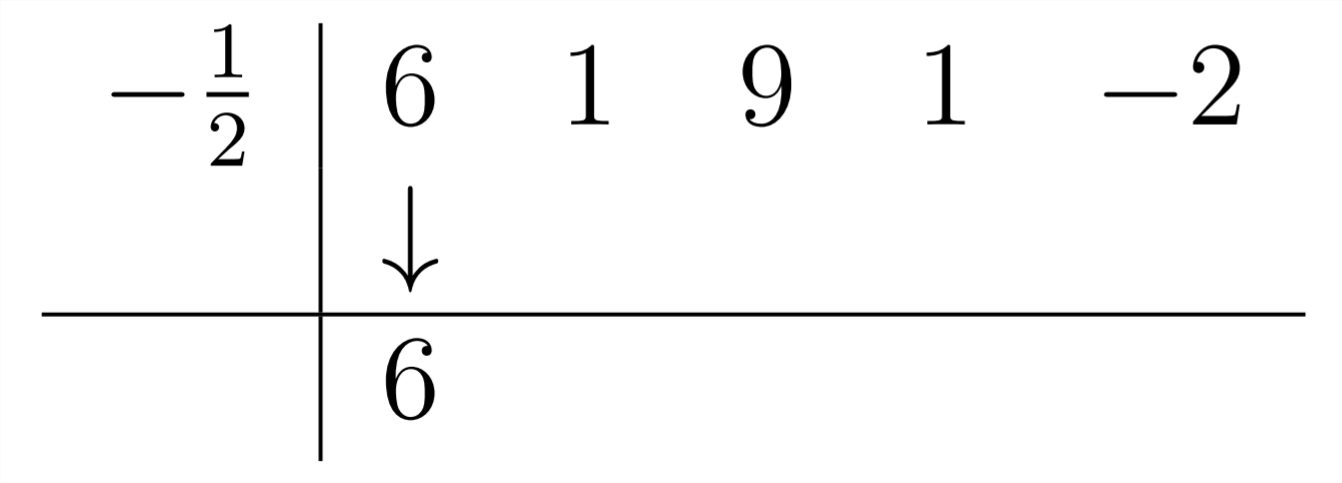
$clipboard_e8e2d3b3aba2efeafef80d8f1c416d671.png$
Entonces, procedemos como de costumbre:
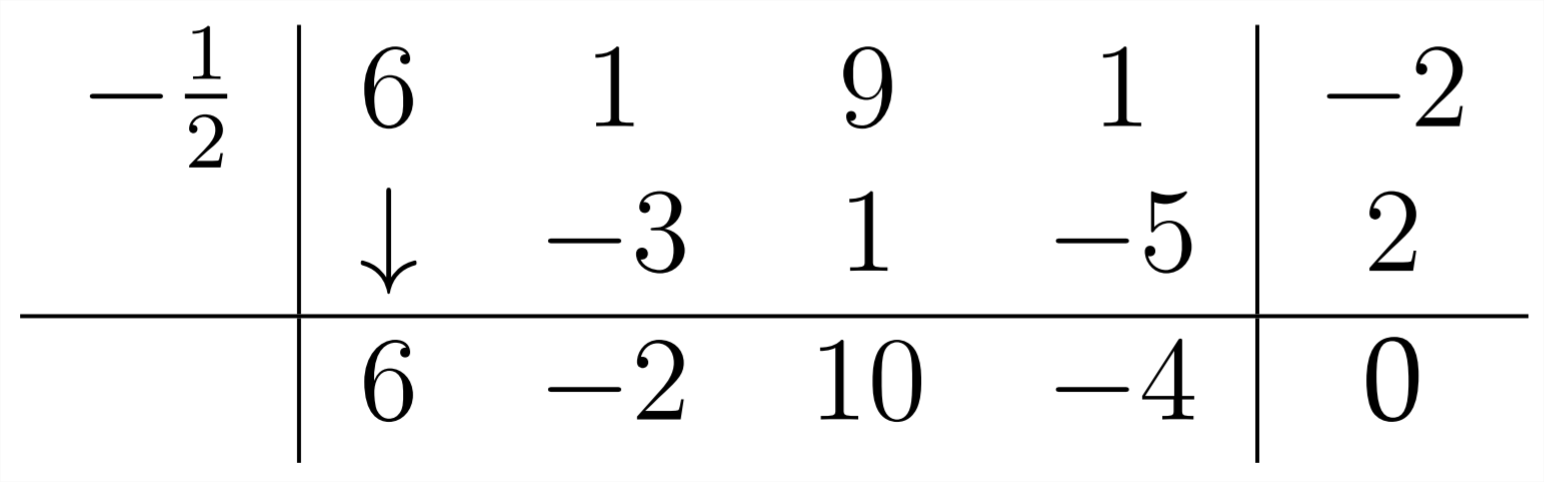
$clipboard_ef914c9a9ff29973189caf206882f8424.png$
Observe que, de nuevo, tenemos un cero resto. También, observe que cada coeficiente en nuestra respuesta tiene un factor común del$2,$ cual era el coeficiente del$x$ en el$2 x+1,$ que originalmente íbamos a dividir por. Lo que hemos hecho aquí no es división por$2 x+1,$ sino división por$x+\frac{1}{2}$
Entonces, al final, nuestro trabajo nos dice que:
\ [
\ frac {6 x^ {4} +x^ {3} +9 x^ {2} +x-2} {x+\ frac {1} {2}} =6 x^ {3} -2 x^ {2} +10 x-4
\]
y
\ [
6 x^ {4} +x^ {3} +9 x^ {2} +x-2=\ left (x+\ frac {1} {2}\ right)\ left (6 x^ {3} -2 x^ {2} +10 x-4\ right)
\]
Observe que si facetamos el factor común de 2 de nuestra respuesta, podemos multiplicarlo de nuevo en el$x+\frac{1}{2}$ y obtener una respuesta para nuestro problema original:
\ [
\ begin {alineado}
6 x^ {4} +x^ {3} +9 x^ {2} +x-2 &=\ izquierda (x+\ frac {1} {2}\ derecha) 2\ izquierda (3 x^ {3} -x^ {2} +5 x-2\ derecha)\\
& =( 2 x+1)\ izquierda (3 x^ {3} -x^ {2} +5 2\ derecha)
\ end {alineado}
\]
Esto significa que:
\ [
\ frac {6 x^ {4} +x^ {3} +9 x^ {2} +x-2} {2 x+1} =3 x^ {3} -x^ {2} +5 x-2
\]
Otra cosa a entender de la División Sintética es que si falta un poder de$x$, entonces deberías incluir un cero como coeficiente de esa potencia

Ejemplo
Usa División Sintética para dividir:
$\frac{x^{3}+4 x-6}{x-2}$
ya que no hay$x^{2}$ término en el polinomio en el que nos estamos sumergiendo, ingresaremos un cero como coeficiente para ese término:
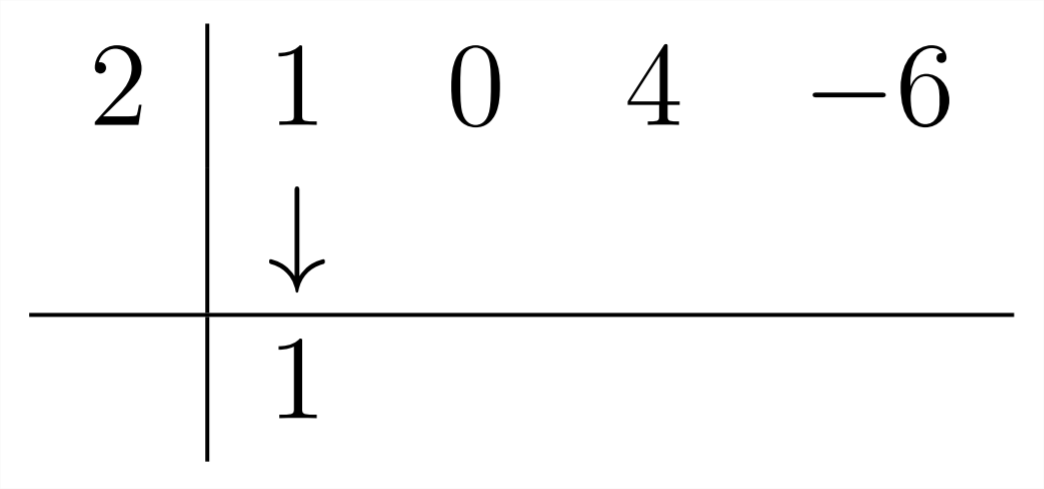
$clipboard_e7467d4926b030a3fdd0b6b420bb8562c.png$
Y luego proceder como de costumbre:
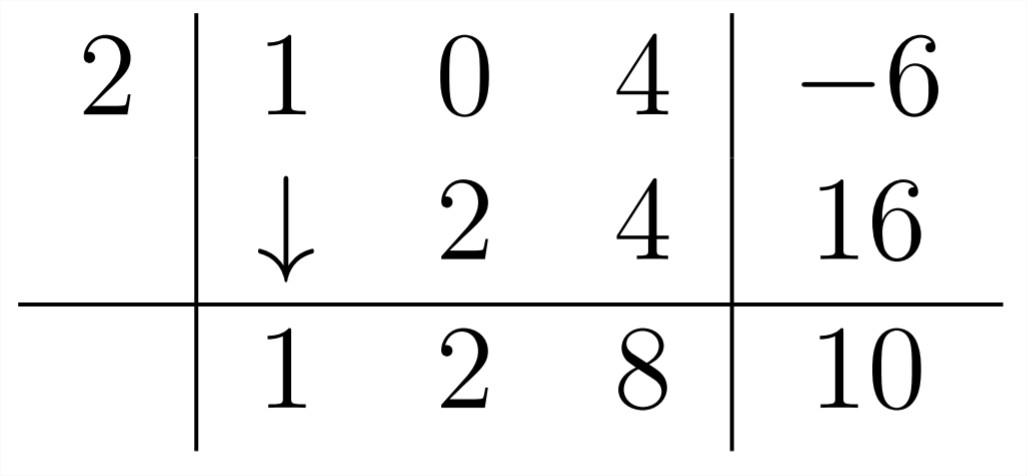
$clipboard_e7e96ca9bd8fa0855d1517e52ee612272.png$
Entonces la respuesta a este problema es$x^{2}+2 x+8$

Ejercicios 2.7
Usa la división sintética para encontrar el cociente en cada problema.
1)$\frac{x^{3}-8 x^{2}+5 x+50}{x-5}$
2)$\frac{x^{3}+5 x^{2}-x-14}{x+2}$
3)$\frac{x^{3}+12 x^{2}+34 x-7}{x+7}$
4)$\frac{x^{3}-10 x^{2}+23 x-6}{x-3}$
5)$\frac{x^{4}-15 x^{2}+10 x+24}{x+4}$
6)$\frac{x^{4}-3 x^{3}+4 x^{2}-36}{x-3}$
7)$\frac{x^{4}-2 x^{3}-x+10}{x-2}$
8)$\frac{x^{4}-16 x^{2}-5 x-24}{x+4}$
9)$\frac{2 x^{4}-x^{3}+2 x-1}{2 x-1}$
10)$\frac{3 x^{4}+x^{3}-3 x+1}{3 x+1}$
11)$\frac{3 x^{4}-8 x^{3}+9 x^{2}-2 x-2}{3 x+1}$
12)$\frac{6 x^{4}-7 x^{3}+5 x^{2}-17 x+10}{3 x-2}$
13)$\frac{2 x^{3}+7 x^{2}+6 x-5}{2 x-1}$
14)$\frac{3 x^{4}-x^{3}-21 x^{2}-11 x+6}{3 x-1}$