7.3: Círculo de Unidad

Objetivos de aprendizaje

• Encuentre valores de función para el seno y coseno de 30° o\((\frac{\pi}{6})\) ,45° o\((\frac{\pi}{4})\), y 60° o\((\frac{\pi}{3})\).
• Identificar el dominio y rango de funciones sinusoidales y cosenales.
• Encuentra ángulos de referencia.
• Utilice ángulos de referencia para evaluar funciones trigonométricas.

¿Buscas emoción? Entonces considera un paseo en el Singapore Flyer, la noria más alta del mundo. Ubicada en Singapur, la noria se eleva a una altura de 541 pies, ¡un poco más de una décima de milla! Descrita como una rueda de observación, los ciclistas disfrutan de vistas espectaculares mientras viajan desde el suelo hasta la cima y vuelven a bajar en un patrón repetitivo. En esta sección, examinaremos este tipo de movimiento giratorio alrededor de un círculo. Para ello, necesitamos definir primero el tipo de círculo, y luego colocar ese círculo en un sistema de coordenadas. Entonces podemos discutir el movimiento circular en términos de los pares de coordenadas.

Figura\(\PageIndex{1}\): El Singapore Flyer es la noria más alta del mundo. (crédito: “Vibin JK” /Flickr)

Encontrar valores de función para el seno y el coseno

Para definir nuestras funciones trigonométricas, comenzamos dibujando un círculo unitario, un círculo centrado en el origen con radio 1, como se muestra en la Figura\(\PageIndex{2}\). El ángulo (en radianes) que\(t\) intercepta forma un arco de longitud\(s\). Usando la fórmula\(s=rt\), y sabiendo eso\(r=1\), vemos eso para un círculo unitario,\(s=t\).

Recordemos que los ejes x e y dividen el plano de coordenadas en cuatro cuartos llamados cuadrantes. Etiquetamos estos cuadrantes para imitar la dirección que barría un ángulo positivo. Los cuatro cuadrantes están etiquetados I, II, III y IV.

Para cualquier ángulo\(t,\) podemos etiquetar la intersección del lado terminal y el círculo unitario como por sus coordenadas,\((x,y)\). Las coordenadas\(x\) y\(y\) serán las salidas de las funciones trigonométricas\(f(t)= \cos t\) y\( f(t)= \sin t\), respectivamente. Esto significa\(x= \cos t\) y\(y= \sin t\).

Figura\(\PageIndex{2}\): Círculo unitario donde el ángulo central es\(t\) radianes

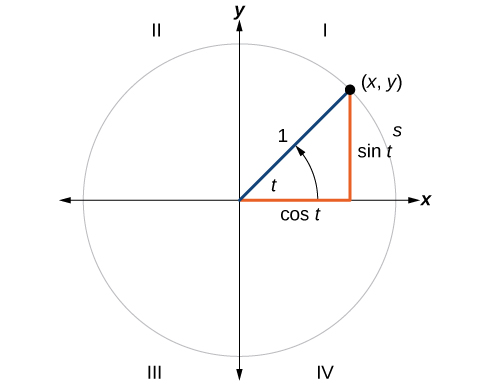
CIRCULO UNIDAD

Un círculo unitario tiene un centro en\((0,0)\) y un radio\(1\). La longitud del arco interceptado es igual a la medida radianes del ángulo central\(t\).

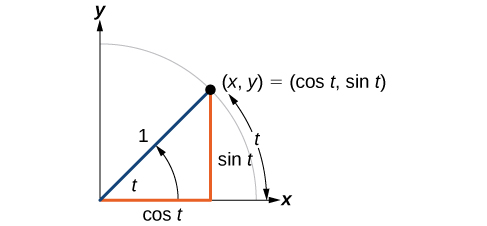
Dejar\((x,y)\) ser el punto final en el círculo unitario de un arco de longitud de arco\(s\). Las\((x,y)\) coordenadas de este punto pueden describirse como funciones del ángulo.

Definición de funciones de seno y coseno

Ahora que tenemos nuestro círculo unitario etiquetado, podemos aprender cómo se relacionan las\((x,y)\) coordenadas con la longitud y el ángulo del arco. La función seno relaciona un número real\(t\) con la\(y\) coordenada -del punto donde el ángulo correspondiente intercepta el círculo unitario. Más precisamente, el seno de un ángulo\(t\) es igual al\(y\) -valor del punto final en el círculo unitario de un arco de longitud\(t\). En la Figura\(\PageIndex{3}\), el seno es igual a\(y\). Como todas las funciones, la función sinusoidal tiene una entrada y una salida. Su entrada es la medida del ángulo; su salida es la\(y\) coordenada del punto correspondiente en el círculo unitario.

La función coseno de un ángulo\(t\) es igual al\(x\) -valor del punto final en el círculo unitario de un arco de longitud\(t\). En la Figura\(\PageIndex{1}\), el coseno es igual a x.

Figura\(\PageIndex{3}\)

Porque se entiende que seno y coseno son funciones, no siempre necesitamos escribirlas con paréntesis:\(\sin t\) es lo mismo que\(\sin (t)\) y\(\cos t\) es lo mismo que\(\cos (t)\). Asimismo,\(\cos ^2 t\) es una notación taquigráfica de uso común para\(( \cos (t))^2\). Tenga en cuenta que muchas calculadoras y computadoras no reconocen la notación taquigráfica. En caso de duda, use los paréntesis adicionales al ingresar cálculos en una calculadora o computadora.

FUNCIONES SINOIS Y COSINO

Si\(t\) es un número real y un punto\((x,y)\) en el círculo unitario corresponde a un ángulo de\(t\), entonces

$$$$

\[ \begin{align} \cos t & = x \\ \sin t & = y \end{align}\]

Cómo: Dado un punto\(P(x,y)\) on the unit circle corresponding to an angle of \( t\), find the sine and cosine

1. El seno de\(t\) es igual a la\(y\) coordenada -del punto\(P\):\( \sin t=y\).
2. El coseno de\(t\) es igual a la\(x\) coordenada -del punto\(P\):\( \cos t=x\).

Ejemplo\(\PageIndex{1}\): Finding Function Values for Sine and Cosine

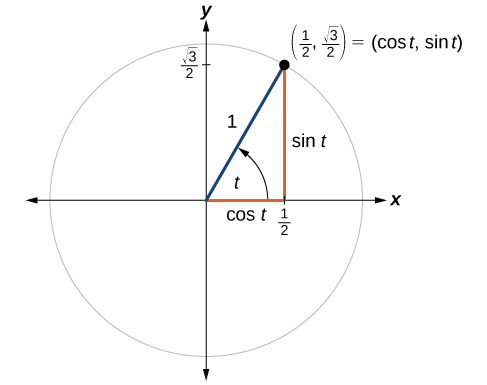
Punto\(P\) es un punto en el círculo unitario correspondiente a un ángulo de\(t\), como se muestra en la Figura\(\PageIndex{4}\). Encontrar\(\cos (t)\) y\(\sin (t)\).

Figura\(\PageIndex{4}\)

Solución

Sabemos que\(\cos t \) es la\(x\) coordenada del punto correspondiente en el círculo unitario y\(\sin t\) es la\(y\) coordenada del punto correspondiente en el círculo unitario. Entonces:

\(\begin{align*} x & = \cos t= \frac{1}{2} \\ y & = \sin t= \frac{\sqrt{3}}{2} \end{align*}\)

$$$$

Pruébalo\(\PageIndex{1}\)

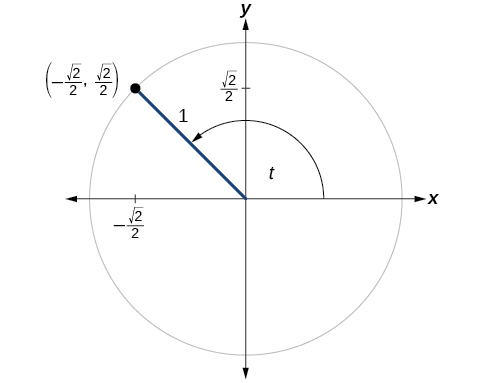
Un cierto ángulo\(t\) corresponde a un punto en el círculo unitario\(\left(−\dfrac{\sqrt{2}}{2},\dfrac{\sqrt{2}}{2}\right)\) como se muestra en la Figura\(\PageIndex{5}\). Encontrar\(\cos t\) y\(\sin t\).

Figura\(\PageIndex{5}\)

Contestar

\(\cos (t)=−\dfrac{ \sqrt{2} }{2}, \sin (t)=\dfrac {\sqrt{2}}{2} \)

Encontrar senos y cosenos de ángulos en un eje

Para los ángulos cuadrantrales, el punto correspondiente en el círculo unitario cae sobre el eje\(x\) - o\(y\) -eje. En ese caso, podemos calcular fácilmente coseno y seno a partir de los valores de\(x\) y\(y\).

Ejemplo\(\PageIndex{2}\): Calculating Sines and Cosines along an Axis

Encuentra\(\cos (90°)\) y\(\sin (90°).\)

Solución

Moverse en\(90°\) sentido antihorario alrededor del círculo unitario desde el\(x\) eje positivo nos lleva a la parte superior del círculo, donde están las\((x,y)\) coordenadas (0, 1), como se muestra en la Figura\(\PageIndex{6}\).

Figura\(\PageIndex{6}\)

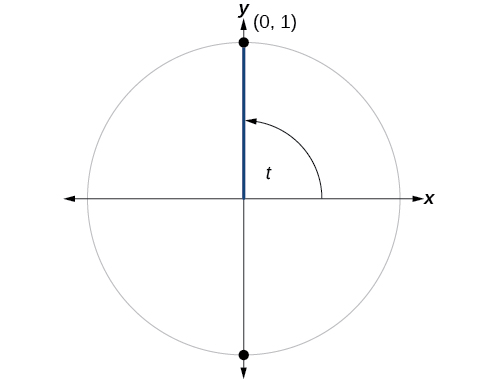
Usando nuestras definiciones de coseno y seno,

\(\begin{align*} x &= \cos t = \cos (90°) = 0 \\ y &= \sin t = \sin (90°) = 1 \end{align*} \)

$$$$

El coseno de 90° es 0; el seno de 90° es 1.

Pruébalo\(\PageIndex{2}\)

Encuentra coseno y seno del ángulo\(π\).

Contestar

\(\cos (π)=−1, \sin (π)=0\)

La identidad pitagórica

Ahora que podemos definir seno y coseno, aprenderemos cómo se relacionan entre sí y con el círculo unitario. Recordemos que la ecuación para el círculo unitario es\(x^2+y^2=1\). Porque\(x= \cos t\) y\(y=\sin t\), podemos sustituir\( x\) y\(y\) para obtener\(\cos ^2 t+ \sin ^2 t=1.\) Esta ecuación,\( \cos ^2 t+ \sin ^2 t=1,\) se conoce como la Identidad Pitagórica. Ver Figura\(\PageIndex{7}\).

Figura\(\PageIndex{7}\)

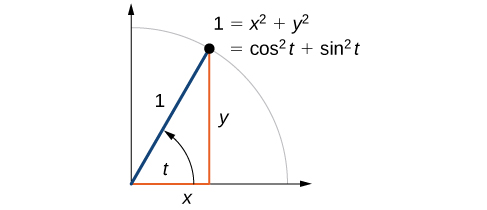
Podemos usar la Identidad Pitagórica para encontrar el coseno de un ángulo si conocemos el seno, o viceversa. Sin embargo, debido a que la ecuación arroja dos soluciones, necesitamos un conocimiento adicional del ángulo para elegir la solución con el signo correcto. Si conocemos el cuadrante donde está el ángulo, podemos elegir fácilmente la solución correcta.

IDENTIDAD PITAGOREA

La Identidad Pitagórica afirma que, para cualquier número real\(t\),

\[ \cos^2 t+ \sin^2 t=1  \]

Cómo: Dado el seno de algún ángulo t y su ubicación cuadrante, encontrar el coseno de t

1. Sustituir el valor conocido de\(\sin (t)\) en la Identidad Pitagórica.
2. Resolver para\( \cos (t)\).
3. Elija la solución con el signo apropiado para los\(x\) -valores en el cuadrante donde\(t\) se encuentra.

Ejemplo\(\PageIndex{3}\): Finding a Cosine from a Sine or a Sine from a Cosine

Si\(\sin (t)=\dfrac{3}{7}\) y\(t\) está en el segundo cuadrante, encuentra\( \cos (t)\).

Solución

Si dejamos caer una línea vertical desde el punto sobre el círculo unitario correspondiente a\(t\), creamos un triángulo rectángulo, a partir del cual podemos ver que la Identidad Pitagórica es simplemente un caso del Teorema de Pitágoras. Ver Figura\(\PageIndex{8}\).

Figura\(\PageIndex{8}\)

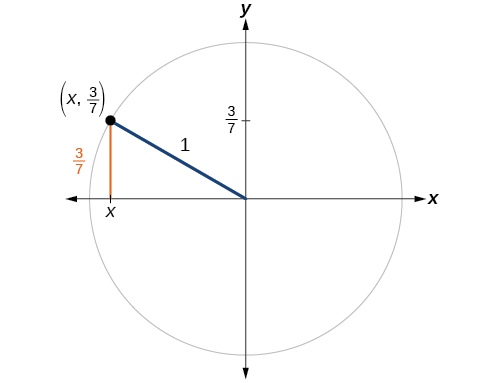
Sustituyendo el valor conocido por seno en la Identidad Pitagórica,

\[\begin{align*} \cos ^2 (t)+ \sin ^2(t) &=1 \\  \cos ^2(t)+\dfrac{9}{49} &=1 \\ \cos ^2(t) & = \dfrac{40}{49} \\  \cos (t) &=± \sqrt{\dfrac{40}{49}}=±\dfrac{\sqrt{40}}{7}=±\dfrac{2\sqrt{10}}{7} \end{align*}\]

Debido a que el ángulo está en el segundo cuadrante, sabemos que el\(x\) -valor es un número real negativo, por lo que el coseno también es negativo. Entonces

\[ \cos (t)=−\dfrac{2\sqrt{10}}{7} \nonumber \]

Pruébalo\(\PageIndex{3}\)

Si\(\cos (t)=\dfrac{24}{25}\) y\(t\) está en el cuarto cuadrante, encuentra\( \sin (t)\).

Contestar

\(\sin (t)=−\dfrac{7}{25}\)

Encontrar senos y cosenos de ángulos especiales

Ya hemos aprendido algunas propiedades de los ángulos especiales, como la conversión de radianes a grados. También podemos calcular senos y cosenos de los ángulos especiales utilizando la Identidad Pitagórica y nuestro conocimiento de los triángulos.

Hallazgo de senos y cosenos de ángulos de 45°

Primero, veremos ángulos de\(45°\) o\(\dfrac{π}{4}\), como se muestra en la Figura\(\PageIndex{9}\). Un\(45°–45°–90°\) triángulo es un triángulo isósceles, por lo que las\(y\) coordenadas\(x\) - y -del punto correspondiente en el círculo son las mismas. Debido a que los\(y\) valores x y -son los mismos, los valores de seno y coseno también serán iguales.

Figura\(\PageIndex{9}\)

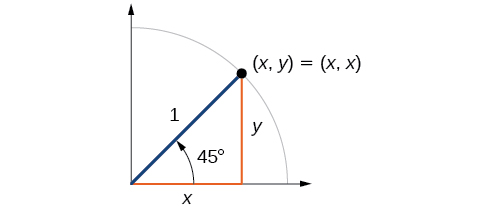
A\(t=\frac{π}{4}\), que es de 45 grados, el radio del círculo unitario biseca el primer ángulo cuadrangular. Esto significa que el radio se encuentra a lo largo de la línea\(y=x\). Un círculo unitario tiene un radio igual a 1. Entonces, el triángulo rectángulo formado debajo de la línea\(y=x\) tiene lados\(x\) y\(y\) (con\(y=x),\) y un radio = 1. Ver Figura\(\PageIndex{10}\).

Figura\(\PageIndex{10}\)

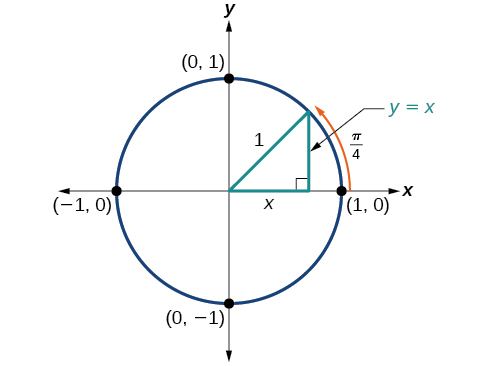
Del Teorema de Pitágoras obtenemos

\[x^2+y^2=1 \nonumber \]

Sustituyendo\(y=x\), obtenemos

\[x^2+x^2=1 \nonumber \]

Combinando términos similares que obtenemos

\[2x^2=1 \nonumber \]

Y resolviendo para\(x\), obtenemos

\[\begin{align*} x^2 &=\dfrac{1}{2} \\ x &=±\dfrac{1}{\sqrt{2}} \end{align*}  \]

En el cuadrante I,\(x=\dfrac{1}{\sqrt{2}}\).

A\(t=\dfrac{π}{4}\) o 45 grados,

\[\begin{align*} (x,y) & =(x,x)=(\dfrac{1}{\sqrt{2}},\dfrac{1}{\sqrt{2}}) \\ x &= \dfrac{1}{\sqrt{2}}, \; y=\dfrac{1}{\sqrt{2}} \\ \cos t &= \dfrac{1}{\sqrt{2}}, \; \sin t=\dfrac{1}{\sqrt{2}} \end{align*}  \]

Si luego racionalizamos a los denominadores, obtenemos

\[ \begin{align*} \cos t &= \dfrac{1}{\sqrt{2}}\dfrac{\sqrt{2}}{\sqrt{2}} \\ &= \dfrac{\sqrt{2}}{2} \\ \sin t &= \dfrac{1}{\sqrt{2}} \dfrac{\sqrt{2}}{\sqrt{2}}  \\ &=\dfrac{\sqrt{2}}{2} \end{align*}\]

Por lo tanto, las\((x,y)\) coordenadas de un punto en un círculo de radio\(1\) en un ángulo de\(45°\) son\(\left(\dfrac{\sqrt{2}}{2},\dfrac{\sqrt{2}}{2}\right)\).

Hallazgo de senos y cosenos de ángulos de 30° y 60°

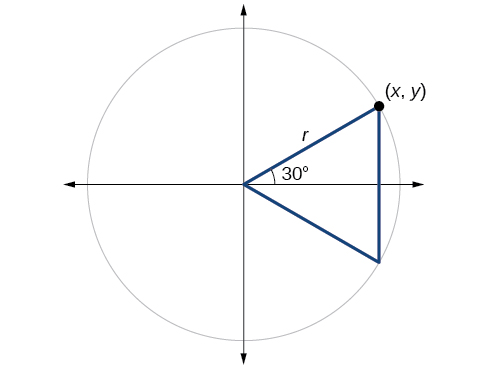
A continuación, encontraremos el coseno y el seno en un ángulo de\(30°,\) o\(\tfrac{π}{6}\). Primero, dibujaremos un triángulo dentro de un círculo con un lado en ángulo de\(30°,\) y otro en un ángulo de\(−30°,\) como se muestra en la Figura\(\PageIndex{11}\). Si los dos triángulos rectos resultantes se combinan en un triángulo grande, observe que los tres ángulos de este triángulo más grande serán\(60°,\) como se muestra en la Figura\(\PageIndex{12}\).

Figura\(\PageIndex{11}\)

Figura\(\PageIndex{12}\)

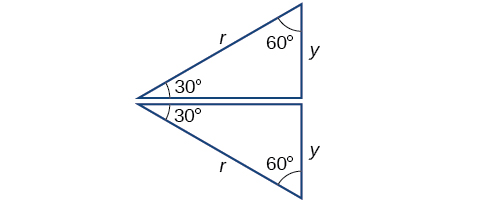
Debido a que todos los ángulos son iguales, los lados también son iguales. La línea vertical tiene longitud\(2y\), y como los lados son todos iguales, también podemos concluir que\(r=2y\) o\(y=\frac{1}{2}r\). Dado que\( \sin t=y\),

\[ \sin \left(\frac{π}{6} \right)=\dfrac{1}{2} \nonumber \]

Y como\(r=1\) en nuestro círculo de unidades,

\[\begin{align*} \sin \left(\frac{π}{6} \right) & = \dfrac{1}{2}(1) \\ &= \dfrac{1}{2} \end{align*}  \]

Usando la Identidad Pitagórica, podemos encontrar el valor del coseno.

\ (\ comenzar {alineado}
\ cos^2\ izquierda (\ frac {π} {6}\ derecha) +\ sin^2\ izquierda (\ frac {π} {6}\ derecha) &= 1 &&\
\ cos^2\ izquierda (\ frac {π} {6}\ derecha) +\ izquierda (\ dfrac {1} {2}\ derecha) ^2 &= 1 &&\
\ cos^2\ izquierda (\ frac {π} {6}\ derecha) &=\ dfrac {3} {4} &&\ text { Utilice la propiedad raíz cuadrada.} \\
\ cos\ left (\ frac {π} {6}\ right) &=\ pm\ sqrt {\ dfrac {3} {4}} =\ dfrac {\ sqrt {3}} {2} &&\ text {Ya que\(y\) es positivo, elige la raíz positiva.}\\
\ end {alineado}\)

Las\((x,y)\) coordenadas para el punto en un círculo de radio\(1\) en un ángulo de\(30°\) son\(\left(\dfrac{\sqrt{3}}{2},\dfrac{1}{2}\right)\). A\(t=\dfrac{π}{3}\) (60°), el radio del círculo unitario, 1, sirve como hipotenusa de un triángulo rectángulo de 30-60-90 grados,\(BAD,\) como se muestra en la Figura\(\PageIndex{13}\). Ángulo\(A\) tiene medida 60°. 60°. En el punto\(B,\) dibujamos un ángulo\(ABC\) con medida de\( 60°\). Sabemos que los ángulos en un triángulo suman a\(180°\), por lo que la medida del ángulo\(C\) es también\(60°\). Ahora tenemos un triángulo equilátero. Debido a que cada lado del triángulo equilátero\(ABC\) tiene la misma longitud, y sabemos que un lado es el radio del círculo unitario, todos los lados deben ser de longitud 1.

Figura\(\PageIndex{13}\)

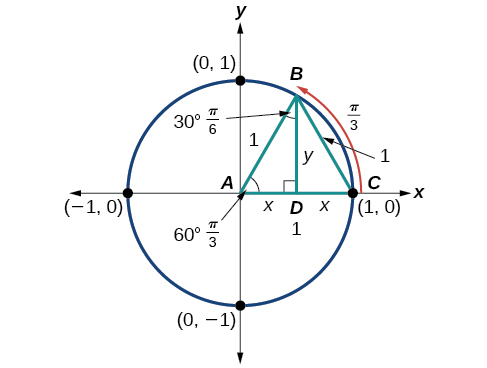
La medida del ángulo\(ABD\) es de 30°. Entonces, si es doble, el ángulo\(ABC\) es de 60°. \(BD\)es la bisectriz perpendicular de\(AC\), por lo que corta por\(AC\) la mitad. Esto significa que\(AD\) es\( \dfrac{1}{2}\) el radio, o\(\dfrac{1}{2}.\) Aviso que\(AD\) es la\(x\) coordenada -del punto\(B\), que está en la intersección del ángulo de 60° y el círculo unitario. Esto nos da un triángulo\(BAD\) con hipotenusa de 1 y lado\(x\) de longitud\(\dfrac{1}{2}\).

Del teorema de Pitágoras, obtenemos

\[x^2+y^2=1 \nonumber \]

Sustituyendo\(x=\frac{1}{2}\), obtenemos

\[ \left(  \dfrac{1}{2}  \right)^2+y^2=1 \nonumber \]

Resolviendo para\(y\), obtenemos

\[\begin{align*} \dfrac{1}{4}+y^2 &=1 \\ y^2 &=1−\dfrac{1}{4} \\ y^2 &= \dfrac{3}{4} \\ y &=± \dfrac{\sqrt{3}}{2} \end{align*}\]

Ya que\(t=\dfrac{π}{3}\) tiene el lado terminal en el cuadrante I donde la\(y\) coordenada -es positiva, elegimos\(y=\dfrac{\sqrt{3}}{2}\), el valor positivo.

A\(t=\dfrac{π}{3}\) (60°), las\((x,y)\) coordenadas para el punto en un círculo de radio\(1\) en un ángulo de\(60°\) son\(\left(\dfrac{1}{2},\dfrac{\sqrt{3}}{2}\right)\), así podemos encontrar el seno y el coseno.

\( (x, y) = \left( \dfrac{1}{2}, \dfrac{ \sqrt{3} }{2} \right) \)

\( x = \dfrac{1}{2}, \; y = \dfrac{ \sqrt{3} }{2} \)

\( \cos t = \dfrac{1}{2}, \; \sin t = \dfrac{ \sqrt{3} }{2} \)

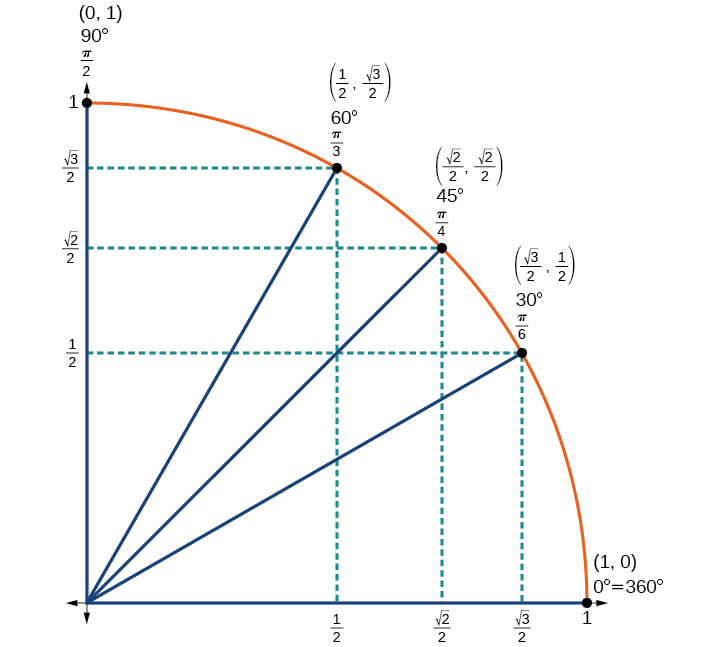
Ahora hemos encontrado los valores de coseno y seno para todos los ángulos más comúnmente encontrados en el primer cuadrante del círculo unitario. \(\PageIndex{1}\)En la tabla se resumen estos valores.

Mesa\(\PageIndex{1}\)

Ángulo	0	\(\dfrac{π}{6}\), o 30	\(\dfrac{π}{4}\), o 45°	\(\dfrac{π}{3}\), o 60°	\(\dfrac{π}{2}\), o 90°
Coseno	1	\(\dfrac{\sqrt{3}}{2}\)	\(\dfrac{\sqrt{2}}{2}\)	\(\dfrac{1}{2}\)	0
Sine	0	\(\dfrac{1}{2}\)	\(\dfrac{\sqrt{2}}{2}\)	\(\dfrac{\sqrt{3}}{2}\)	1

La figura\(\PageIndex{14}\) muestra los ángulos comunes en el primer cuadrante del círculo unitario.

Figura\(\PageIndex{14}\)

Uso de una calculadora para encontrar seno y coseno

Para encontrar el coseno y el seno de ángulos distintos de los ángulos especiales, recurrimos a una computadora o calculadora. Tenga en cuenta: La mayoría de las calculadoras se pueden establecer en modo “grado” o “radián”, que le dice a la calculadora las unidades para el valor de entrada. Cuando evaluamos\( \cos (30)\) en nuestra calculadora, la evaluará como el coseno de 30 grados si la calculadora está en modo grados, o el coseno de 30 radianes si la calculadora está en modo radianes.

Cómo: Dado un ángulo en radianes, use una calculadora gráfica para encontrar el coseno

1. Si la calculadora tiene modo grado y modo radianes, configúrela en modo radianes.
2. Presione la tecla COS.
3. Ingresa el valor radián del ángulo y presiona la tecla entre paréntesis “)”.
4. Presione ENTER.

Ejemplo\(\PageIndex{4}\): Using a Graphing Calculator to Find Sine and Cosine

Evaluar\( \cos \left(\dfrac{5π}{3}\right)\) usando una calculadora gráfica o computadora.

Solución

Introduzca las siguientes pulsaciones de teclas:

\(\mathrm{COS( 5 × π ÷ 3 ) \; ENTER}\)

\[ \cos \left(\dfrac{5π}{3}\right)=0.5 \nonumber\]

Análisis

Podemos encontrar el coseno o seno de un ángulo en grados directamente en una calculadora con modo grados. Para calculadoras o software que usan solo modo radianes, podemos encontrar el signo de\(20°\), por ejemplo, al incluir el factor de conversión a radianes como parte de la entrada:

\[\mathrm{SIN( 20 × π ÷ 180 ) \; ENTER} \nonumber\]

Pruébalo\(\PageIndex{4}\)

Evaluar\(\sin \left( \dfrac{π}{3} \right) \).

Contestar

aproximadamente 0.866025403

Identificación del dominio y rango de funciones sinusoidales y cosenales

Ahora que podemos encontrar el seno y el coseno de un ángulo, necesitamos discutir sus dominios y rangos. ¿Cuáles son los dominios de las funciones seno y coseno? Es decir, ¿cuáles son los números más pequeños y mayores que pueden ser entradas de las funciones? Debido a que los ángulos menores que 0 y los ángulos mayores que 2π todavía se pueden graficar en el círculo unitario y tienen valores reales de\(x, \; y\)\(r\), y, no hay límite inferior o superior a los ángulos que pueden ser entradas a las funciones seno y coseno. La entrada a las funciones seno y coseno es la rotación desde el\(x\) eje positivo, y ese puede ser cualquier número real.

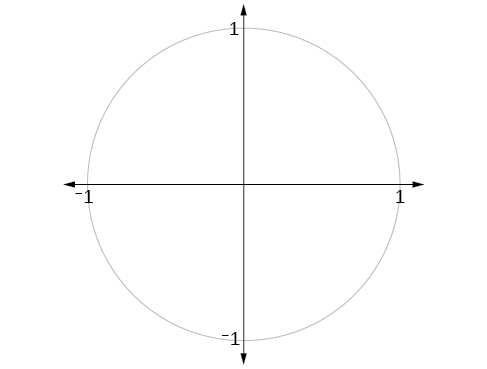
¿Cuáles son los rangos de las funciones seno y coseno? ¿Cuáles son los menores y mayores valores posibles para su producción? Podemos ver las respuestas examinando el círculo unitario, como se muestra en la Figura\(\PageIndex{15}\). Los límites de la\(x\) coordenada -son\( [−1,1]\). Los límites de la\(y\) coordenada -también lo son\([−1,1]\). Por lo tanto, el rango de las funciones tanto seno como coseno es\([−1,1]\).

Figura\(\PageIndex{15}\)

Encontrar ángulos de referencia

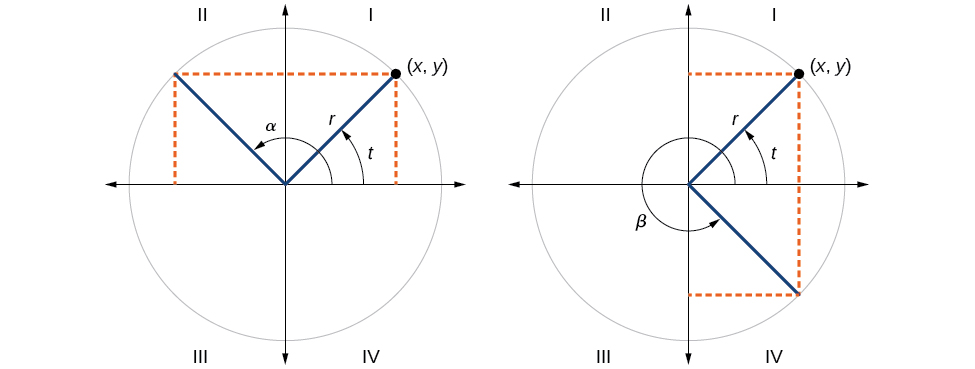
Hemos discutido encontrar el seno y el coseno para los ángulos en el primer cuadrante, pero ¿y si nuestro ángulo está en otro cuadrante? Para cualquier ángulo dado en el primer cuadrante, hay un ángulo en el segundo cuadrante con el mismo valor sinusoidal. Debido a que el valor de seno es la\(y\) coordenada -en el círculo unitario, el otro ángulo con el mismo seno compartirá el mismo\(y\) -valor, pero tendrá el\(x\) valor -opuesto. Por lo tanto, su valor coseno será el opuesto al valor del coseno del primer ángulo.

De igual manera, habrá un ángulo en el cuarto cuadrante con el mismo coseno que el ángulo original. El ángulo con el mismo coseno compartirá el mismo\(x\) -valor pero tendrá el\(y\) -valor opuesto. Por lo tanto, su valor sinusoidal será el opuesto al valor sinusoidal del ángulo original.

Como se muestra en la Figura\(\PageIndex{16}\), el ángulo\(α\) tiene el mismo valor sinusoidal que el ángulo\(t\); los valores coseno son opuestos. El ángulo\(β\) tiene el mismo valor coseno que el ángulo\(t\); los valores sinusoidales son opuestos.

\ (\ begin {array} {ccc}\ sin (t) =\ sin (α) &\ text {y} &\ cos (t) = -\ cos (α)\
\\ sin (t) = -\ sin (β) &\ text {y} &\ cos (t) =\ cos (β)\
\ end {array}\)

Figura\(\PageIndex{16}\)

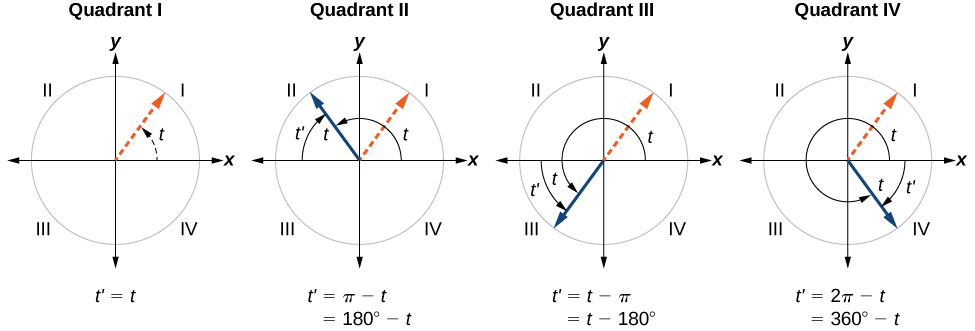
Recordemos que el ángulo de referencia de un ángulo es el ángulo agudo\(t\),, formado por el lado terminal del ángulo\(t\) y el eje horizontal. Un ángulo de referencia es siempre un ángulo entre\(0\) y\(90°\), o\(0\) y\(\dfrac{π}{2}\) radianes. Como podemos ver en la Figura\(\PageIndex{17}\), para cualquier ángulo en los cuadrantes II, III o IV, hay un ángulo de referencia en el cuadrante I.

Figura\(\PageIndex{17}\)

Cómo: Dado un ángulo entre\(0\) and \(2π\), find its reference angle

1. Un ángulo en el primer cuadrante es su propio ángulo de referencia.
2. Para un ángulo en el segundo o tercer cuadrante, el ángulo de referencia es\(|π−t|\) o\(|180°−t|\).
3. Para un ángulo en el cuarto cuadrante, el ángulo de referencia es\(2π−t\) o\(360°−t.\)
4. Si un ángulo es menor\(0\) o mayor que\(2π,\) sumar o restar\(2π\) tantas veces como sea necesario para encontrar un ángulo equivalente entre\(0\) y\(2π\).

Ejemplo\(\PageIndex{5}\): Finding a Reference Angle

Encuentre el ángulo de referencia de\(225°\) como se muestra en la Figura\(\PageIndex{18}\).

Figura\(\PageIndex{18}\)

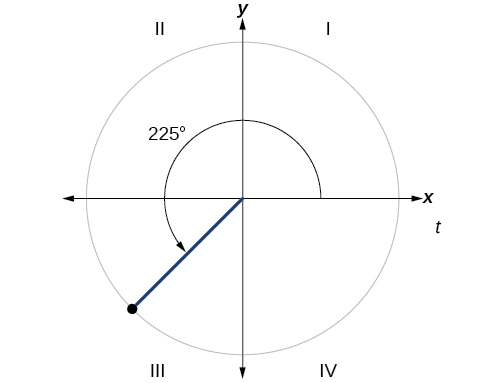
Solución

Porque\( 225°\) está en el tercer cuadrante, el ángulo de referencia es

\[|(180°−225°)|=|−45°|=45° \nonumber \]

Pruébalo\(\PageIndex{5}\)

Encuentra el ángulo de referencia de\(\frac{5π}{3}\).

Contestar

(\ dfrac {π} {3}\)

Uso de ángulos de referencia

Ahora tomemos un momento para reconsiderar la noria introducida al inicio de esta sección. Supongamos que un jinete toma una fotografía mientras se detiene veinte pies sobre el nivel del suelo. Luego, el jinete gira tres cuartas partes del camino alrededor del círculo. ¿Cuál es la nueva elevación del piloto? Para responder preguntas como esta, necesitamos evaluar las funciones sinusoidales o cosenales en ángulos que sean mayores a 90 grados o en un ángulo negativo. Los ángulos de referencia permiten evaluar funciones trigonométricas para ángulos fuera del primer cuadrante. También se pueden utilizar para encontrar\((x,y)\) coordenadas para esos ángulos. Utilizaremos el ángulo de referencia del ángulo de rotación combinado con el cuadrante en el que se encuentra el lado terminal del ángulo.

Uso de ángulos de referencia para evaluar funciones trigonométricas

Podemos encontrar el coseno y el seno de cualquier ángulo en cualquier cuadrante si conocemos el coseno o seno de su ángulo de referencia. Los valores absolutos del coseno y seno de un ángulo son los mismos que los del ángulo de referencia. El signo depende del cuadrante del ángulo original. El coseno será positivo o negativo dependiendo del signo de los\(x\) -valores en ese cuadrante. El seno será positivo o negativo dependiendo del signo de los\(y\) -valores en ese cuadrante.

Usar ángulos de referencia para encontrar coseno y seno

Los ángulos tienen cosenos y senos con el mismo valor absoluto que los cosenos y los senos de sus ángulos de referencia. El signo (positivo o negativo) se puede determinar a partir del cuadrante del ángulo.

Cómo: Dado un ángulo en posición estándar, encuentre el ángulo de referencia, y el coseno y el seno del ángulo original

1. Mida el ángulo entre el lado terminal del ángulo dado y el eje horizontal. Ese es el ángulo de referencia.
2. Determinar los valores del coseno y seno del ángulo de referencia.
3. Dale al coseno el mismo signo que los\(x\) valores -en el cuadrante del ángulo original.
4. Dale al seno el mismo signo que los\(y\) valores -en el cuadrante del ángulo original.

Ejemplo\(\PageIndex{6}\): Using Reference Angles to Find Sine and Cosine

1. Usando un ángulo de referencia, encuentre el valor exacto de\(\cos (150°)\) y\( \sin (150°)\).
2. Usando el ángulo de referencia, encontrar\( \cos \dfrac{5π}{4}\) y\(\sin \frac{5π}{4}\).

Solución

Esto nos dice que 150° tiene los mismos valores de seno y coseno que 30°, a excepción del signo. Sabemos que

Dado que\(150°\) está en el segundo cuadrante, la\(x\) coordenada -del punto en el círculo es negativa, por lo que el valor del coseno es negativo. La\(y\) coordenada -es positiva, por lo que el valor sinusoidal es positivo.

\(\dfrac{5π}{4}\)está en el tercer cuadrante. Su ángulo de referencia es\( \left| \dfrac{5π}{4} - π \right| = \dfrac{π}{4} \). El coseno y el seno de\(\dfrac{π}{4} \) son ambos\( \dfrac{\sqrt{2}}{2} \). En el tercer cuadrante, ambos\(x\) y\(y\) son negativos, así:

\( \cos \dfrac{5π}{4} = -\dfrac{\sqrt{2}}{2} \)y\(\sin \dfrac{5π}{4} = -\dfrac{\sqrt{2}}{2} \)

Pruébalo\(\PageIndex{6}\)

1. Utilice el ángulo de referencia de\(315°\) para encontrar\( \cos (315°) \) y\(\sin (315°)\).
2. Utilice el ángulo de referencia de\(−\dfrac{π}{6}\) para encontrar\( \cos \left(−\dfrac{π}{6}\right) \) y\( \sin \left(−\dfrac{π}{6}\right)\)

Contestar

1. \( \cos (315°)= \dfrac{\sqrt{2}}{2}, \sin (315°)=\dfrac{–\sqrt{2}}{2}\)
2. \(\cos \left(−\dfrac{π}{6}\right)=\dfrac{\sqrt{3}}{2}, \sin \left(−\dfrac{π}{6}\right)=−\frac{1}{2} \)

Uso de ángulos de referencia para buscar coordenadas

Ahora que hemos aprendido a encontrar los valores de coseno y seno para ángulos especiales en el primer cuadrante, podemos usar simetría y ángulos de referencia para rellenar los valores de coseno y seno para el resto de los ángulos especiales en el círculo unitario. Se muestran en la Figura\(\PageIndex{19}\). Tómese el tiempo para aprender las\((x,y)\) coordenadas de todos los ángulos principales en el primer cuadrante.

Figura\(\PageIndex{19}\): Ángulos especiales y coordenadas de los puntos correspondientes en el círculo unitario

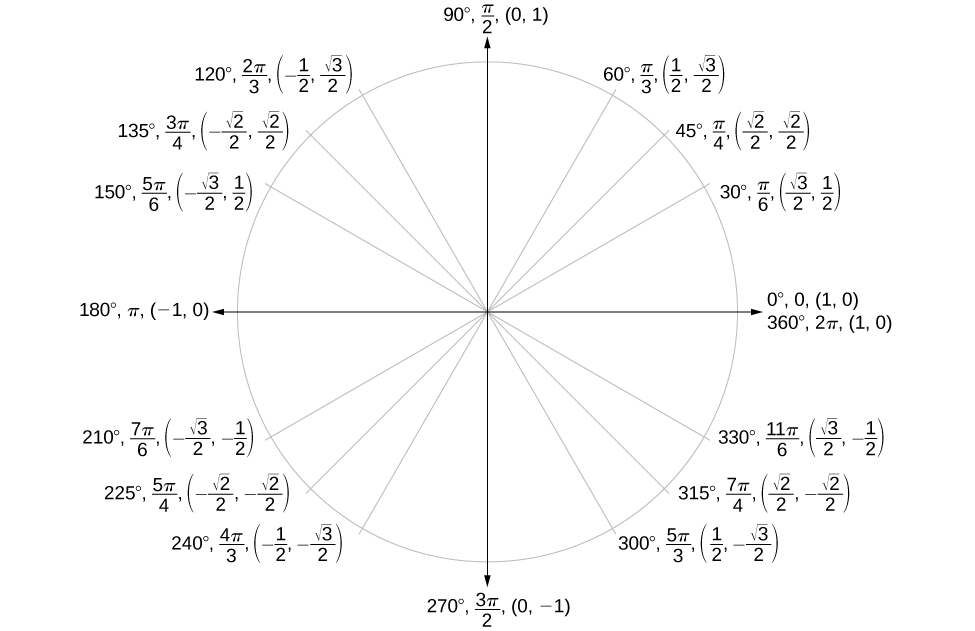
Además de aprender los valores para ángulos especiales, podemos usar ángulos de referencia para encontrar\((x,y)\) coordenadas de cualquier punto en el círculo unitario, usando lo que sabemos de los ángulos de referencia junto con las identidades

\[\begin{align*} x &= \cos t \\ y & = \sin t \end{align*}\]

Primero encontramos el ángulo de referencia correspondiente al ángulo dado. Luego tomamos los valores de seno y coseno del ángulo de referencia, y les damos los signos correspondientes a los\(x\) valores\(y\) - y -del cuadrante.

Cómo: Dado el ángulo de un punto en un círculo y el radio del círculo, encuentre el\((x,y)\) coordinates of the point

1. Encuentre el ángulo de referencia midiendo el ángulo más pequeño con respecto al\(x\) eje.
2. Encuentra el coseno y el seno del ángulo de referencia.
3. Determinar los signos apropiados para\(x\) y\(y\) en el cuadrante dado.

Ejemplo\(\PageIndex{7}\): Using the Unit Circle to Find Coordinates

Encuentra las coordenadas del punto en el círculo unitario en un ángulo de\(\dfrac{7π}{6}\).

Solución

Sabemos que el ángulo\(\dfrac{7π}{6}\) está en el tercer cuadrante.

Primero, encontremos el ángulo de referencia midiendo el ángulo con el\(x\) eje. Para encontrar el ángulo de referencia de un ángulo cuyo lado terminal está en el cuadrante III, encontramos la diferencia del ángulo y\(π\).

\[\dfrac{7π}{6}−π=\dfrac{π}{6} \nonumber \]

A continuación, encontraremos el coseno y el seno del ángulo de referencia:

\[\cos \left( \dfrac{π}{6} \right) =\dfrac{3}{2} \;\;        \sin \left(\dfrac{π}{6}\right)=\dfrac{1}{2} \nonumber \]

Debemos determinar los signos apropiados para\(x\) y\(y\) en el cuadrante dado. Porque nuestro ángulo original está en el tercer cuadrante, donde ambos\(x\) y\(y\) son negativos, tanto el coseno como el seno son negativos.

\[\begin{align*} \cos \left(\dfrac{7π}{6}\right) &=−\dfrac{\sqrt{3}}{2} \\ \sin \left(\dfrac{7π}{6}\right) & =−\dfrac{1}{2} \end{align*}\]

Ahora podemos calcular las\((x,y)\) coordenadas usando las identidades\(x= \cos θ\) y\(y= \sin θ\).

Las coordenadas del punto están\(\left(−\dfrac{\sqrt{3}}{2},−\dfrac{1}{2}\right)\) en el círculo unitario.

Pruébalo\(\PageIndex{7}\)

Encuentra las coordenadas del punto en el círculo unitario en un ángulo de\(\dfrac{5π}{3}\).

Contestar

\(  \left( \dfrac{1}{2},−\dfrac{\sqrt{3}}{2} \right) \)

medios

Acceda a estos recursos en línea para obtener instrucción adicional y práctica con funciones sinusoidales y cosenales.

• Funciones trigonométricas usando el círculo unitario
• Seno y coseno del círculo unitario
• Seno y coseno del círculo unitario y múltiplos de Pi divididos por seis
• Seno y coseno del círculo unitario y múltiplos de Pi divididos por cuatro
• Funciones trigonométricas mediante ángulos de referencia

Ecuaciones Clave

Coseno	\( \cos t=x\)
Sine	\( \sin t=y\)
Identidad pitagórica	\( \cos ^2 t+ \sin ^2 t=1\)

Conceptos clave

• Encontrar los valores de función para el seno y el coseno comienza con dibujar un círculo unitario, que está centrado en el origen y tiene un radio de 1 unidad.
• Usando el círculo unitario, el seno de un ángulo\(t\) es igual al\(y\) -valor del punto final en el círculo unitario de un arco de longitud\(t\) mientras que el coseno de un ángulo\(t\) es igual al\(x\) -valor del punto final. Ver Ejemplo.
• Los valores de seno y coseno se determinan más directamente cuando el punto correspondiente en el círculo unitario cae sobre un eje. Ver Ejemplo.
• Cuando se conoce el seno o coseno, podemos usar la Identidad Pitagórica para encontrar al otro. La identidad pitagórica también es útil para determinar los senos y cosenos de ángulos especiales. Ver Ejemplo.
• Las calculadoras y el software gráfico son útiles para encontrar senos y cosenos si se conoce el procedimiento adecuado para ingresar información. Ver Ejemplo.
• El dominio de las funciones seno y coseno son todos números reales.
• El rango de las funciones senoidal y coseno es\([−1,1]\).
• El seno y el coseno de un ángulo tienen el mismo valor absoluto que el seno y el coseno de su ángulo de referencia.
• Los signos del seno y coseno se determinan a partir de los\(y\) valores x - y -en el cuadrante del ángulo original.
• El ángulo de referencia de un ángulo es el ángulo de tamaño\(t\), formado por el lado terminal del ángulo\(t\) y el eje horizontal. Ver Ejemplo.
• Los ángulos de referencia se pueden utilizar para encontrar el seno y el coseno del ángulo original. Ver Ejemplo.
• Los ángulos de referencia también se pueden utilizar para encontrar las coordenadas de un punto en un círculo. Ver Ejemplo.

Glosario

función coseno

el\(x\) -valor del punto en un círculo unitario correspondiente a un ángulo dado

Identidad pitagórica

un corolario del Teorema de Pitágoras afirmando que el cuadrado del coseno de un ángulo dado más el cuadrado del seno de ese ángulo es igual a 1

función sinusoidal

el\(y\) -valor del punto en un círculo unitario correspondiente a un ángulo dado

círculo de unidad

un círculo con un centro en\((0,0)\) y radio 1.