1.27: Sistema de coordenadas rectangulares

Última actualización
Guardar como PDF

Page ID: 108560

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

En el Capítulo 1, aprendimos que un número real puede representarse como un punto en una recta numérica. En esta sección aprenderemos que un par ordenado de números reales se puede representar como un punto en un plano. Este plano se llama sistema de coordenadas rectangulares o sistema de coordenadas cartesianas que lleva el nombre de un matemático francés, Ren'e Descartes.

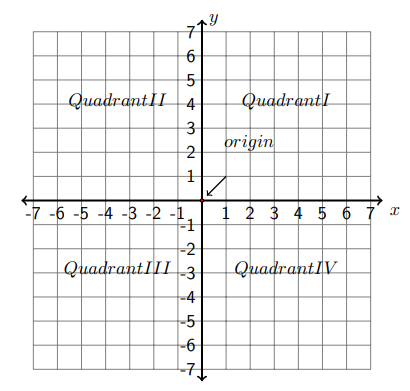
La figura de la página siguiente muestra el sistema de coordenadas rectangulares. Consta de dos líneas numéricas perpendiculares entre sí. La línea horizontal se llama eje x, y la línea vertical se llama$y$ -eje. Las dos líneas numéricas se cruzan en el origen de cada línea numérica y la intersección se denomina origen del sistema de coordenadas. Los ejes dividen el plano en cuatro regiones. Se les llama cuadrantes. De la parte superior derecha a la parte inferior derecha, los cuadrantes se ordenan como I, II, III y IV en sentido contrario a las agujas del reloj.

Cada punto$P$ en el plano está representado por un par ordenado$(x, y),$ que se conoce como las coordenadas del punto$P$. El primer valor se llama$x$ coordenada, y el segundo se llama$y$ -coordenada. La$x$ coordenada mide la distancia del punto desde el$y$ eje -y la$y$ coordenada mide la distancia del punto desde el$x$ eje -eje. Si$x>0,$ el punto está a la derecha del$y$ eje -; si$x<0,$ el punto está a la izquierda del$y$ eje -; si$x=0,$ el punto está en el$y$ eje -eje. Si$y>0,$ el punto está por encima del$x$ eje -; si$y<0,$ el punto está por debajo del$y$ eje -; si$y=0,$ el punto está en el$x$ eje -eje.

$clipboard_e2e2406031be20f6e61740ad0fc8eed78.png$

Ejemplo 25.1

Trazar los puntos dados en el sistema de coordenadas rectangulares.

(A)$(4, 2)$, (B)$(−2, 3)$, (C)$(−3, −1)$, (D)$(2, −4)$ (E)$(0, 1)$, (F)$(−1, 0)$

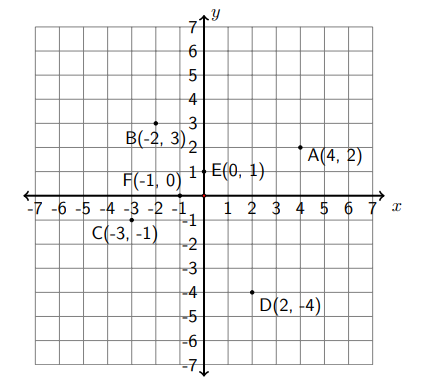
$clipboard_e9a6e5039e1b8dbb92934419f84d7ba81.png$

Para trazar punto$(4,2),$ partimos del origen luego movemos 4 unidades a la derecha y 2 unidades hacia arriba. El punto (4,2) se etiqueta como$A$. Para trazar el punto (-2,3), partimos del origen luego movemos 2 unidades a la izquierda y 3 unidades hacia arriba. El punto (-2,3) está etiquetado como$B .$ Puntos$(\mathrm{C})$ y$(\mathrm{D})$ se trazan de manera similar. Para trazar$(0,1),$ desde el origen, solo nos movemos 1 unidad hacia arriba, por lo que el punto$E$ está en el$y$ eje -eje. De igual manera, el punto (-1,0) se encuentra en el$x$ eje -, 1 unidad a la izquierda del origen. El punto (0,0) es solo el origen del sistema de coordenadas.

Ejemplo 25.2

Determinar las coordenadas de los siguientes puntos:

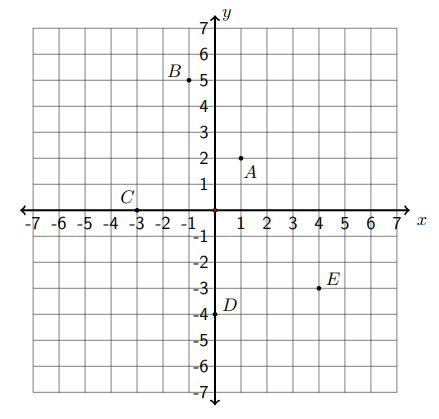
$clipboard_ed3b8116bf64e8a1fa6998851645da509.png$

Punto A: 1 unidad derecha, 2 unidades arriba$(1, 2)$

Punto B: 1 unidad izquierda, 5 unidades arriba$(−1, 5)$

Punto C: 3 unidades a la izquierda, 0 unidades arriba o abajo (−3, 0)

Punto D: 0 unidades izquierda o derecha, 4 unidades abajo (0, −4)

Punto E: 4 unidades a la derecha, 3 unidades hacia abajo (4, −3)

Ecuaciones Lineales en Dos Variables

En el Capítulo 16 resolvimos ecuaciones lineales en una variable. En esta sección, aprenderemos a encontrar soluciones de ecuaciones lineales en dos variables, y cómo representarlas en un sistema de coordenadas rectangulares.

La ecuación$y=2 x+3$ es un ejemplo de una ecuación lineal en dos variables,$x$ y$y$. La solución a esta ecuación es un par ordenado de dos números reales de$(a, b)$ manera que cuando$x$ es reemplazado por$a$ y$y$ es reemplazado por$b,$ la ecuación es una declaración verdadera. Por ejemplo, (1,5) es una solución de$y=2 x+3$ porque cuando sustituimos 1 por$x$ y 5 por$y,$ obtenemos$5=2(1)+3,$ que es una declaración verdadera. El par ordenado (4,3) no es una solución a la ecuación porque sustituir 4 por$x$ y 3 por$y$ no satisface la ecuación i.e$3 \neq 2(4)+3$.

Ejemplo 25.3

Comprobar si los siguientes pares ordenados son soluciones de la ecuación$2 x-3 y=5$.

\[(A) (1,-1) (B) (2,1) (C) \left(\frac{5}{2}, 0\right)\nonumber\]

Para comprobarlo, sustituyamos los valores en nuestra ecuación.

(A)$2(1)-3(-1)=5 \Rightarrow 2+3=5 \Rightarrow 5=5$ Verdadero

(B)$2(2)-3(1)=5 \Rightarrow 4-3=5 \Rightarrow 1=5$ Falso

(C)$2\left(\frac{5}{2}\right)-3(0)=5\Rightarrow 5-0=5 \Rightarrow 5=5$ Verdadero

Por lo tanto$(A)$ y$(C)$ son soluciones y no$(B)$ es una solución.

Del último ejemplo vemos que las soluciones de una ecuación en dos variables son pares ordenados$(x, y)$. Por lo tanto, se pueden representar por puntos en un sistema de coordenadas rectangulares. Al conectar todos los puntos posibles, obtenemos la gráfica de la ecuación.

Ahora vamos a encontrar la gráfica de la ecuación$y=2 x+3$ encontrando pares de soluciones y trazándolos. Ya que solo tenemos una ecuación para dos variables$x$ y$y$, primero podemos elegir algunos$x$ valores, decir$x=-2,-1,0,1,2,$ y luego encontrar sus$y$ valores correspondientes. Por ejemplo, si$x=-2$$y=2(-2)+3=-1 .$ entonces So (-2, -1) es un par de soluciones. Es útil configurar una mesa para realizar un seguimiento.

\ (\ begin {array} {lll}\ text {Valor de} x &\ text {Calcular} y = 2x + 3 &\ text {Par de soluciones}
-2 & y=2 (-2) +3=-1 & (-2, -1)\\
-1 & y=2 (-1) +3=1 & (-1,1)\\
0 & y=2 (0) +3=3 & (0,3)\\
1 y=2 (1) +3=5 & (1,5)\\
2 & y=2 (2) +3=7 & (2,7)
\ end {array}\)

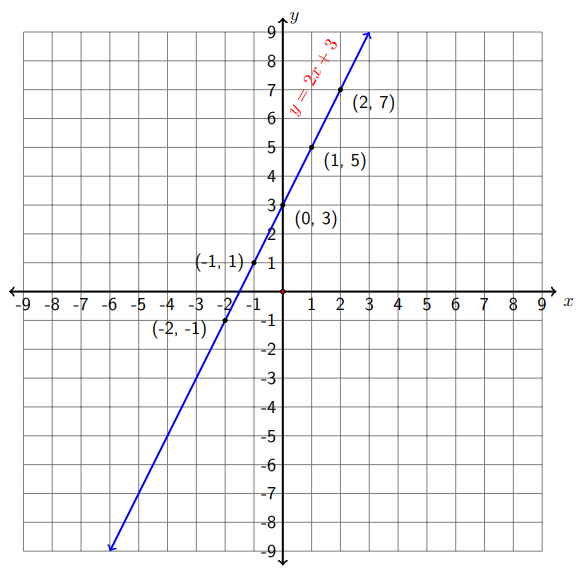
$clipboard_e691e252840d6c1ca849a4d8552805b2a.png$

Después de trazar estos puntos en un sistema de coordenadas rectangulares, es fácil adivinar que la gráfica de$y=2 x+3$ podría ser una línea recta. De hecho, la gráfica de la ecuación$y=2 x+3$ es una línea recta, razón por la cual se le conoce como una ecuación lineal.

Ejemplo 25.4

Grafica la ecuación$3 x+2 y=4$ trazando puntos.

Para graficar la ecuación, primero necesitamos encontrar un par de pares de soluciones. Comencemos resolviendo$y:$

$3 x+2 y=4 \quad \Rightarrow \quad 2 y=-3 x+4 \quad \Rightarrow \quad y=\frac{-3 x+4}{2} \quad \Rightarrow \quad y=\frac{-3 x}{2}+2$

Vamos$x=-4,-2,0,2,4$. Aquí solo se eligen números pares por lo que los resultados no son fracciones.

\ (\ begin {array} {lll}\ text {Valor de} x &\ text {Calcular} y=\ frac {-3 x} {2} +2 &\ text {Par de soluciones}
-4 & y=\ frac {-3 (-4)} {2} +2=8 & (-4,8)\
-2 & y=\ frac {-3 (-2)} {2} +2=5 & (-2,5)\\
0 & y=\ frac {-3 (0)} {2} +2=2 & (0,2)\\
2 & amp; y=\ frac {-3 (2)} {2} +2=-1 & (2, -1)\\
4 & y=\ frac {-3 (4)} {2} +2=-4 & (4, -4)
\ end {array}\)

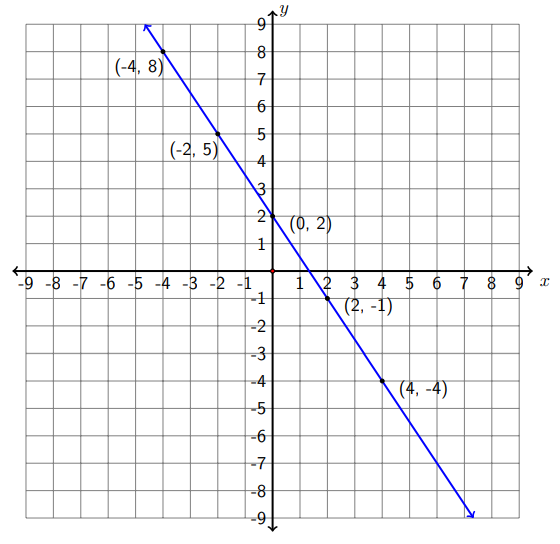
La gráfica de la línea$3 x+2 y=4$ se muestra en la siguiente figura.

$clipboard_e32bb44a80ac3538c31502cf424e4b372.png$

Problema de salida

Grafica la ecuación:$3 x+2 y=8$