1.28: Graficar ecuaciones lineales

Última actualización
Guardar como PDF

Page ID: 108607

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

En general, una ecuación lineal en dos variables es de la forma

\[A x+B y=C\nonumber\]

en el que$A, B, C$ son números reales y$A$ y$B$ no pueden ser ambos$0 .$ A esto se le llama la forma estándar de una ecuación lineal. Aquí hay algunos ejemplos de ecuaciones lineales en forma estándar:

\[3 x+2 y=4, \quad-0.25 x+\frac{2}{3} y=1, \quad-3 x=2, \quad 4 y=3\nonumber\]

Algunas ecuaciones lineales no están escritas en forma estándar, pero pueden transformarse fácilmente en una forma estándar. Por ejemplo, la ecuación lineal se$y=$$-2 x-3$ puede escribir en una forma estándar$2 x+y=-3$ de sumando$2 x$ a ambos lados de la ecuación.

La gráfica de una ecuación lineal es una línea recta en el sistema de coordenadas rectangulares. En el último capítulo aprendimos a trazar una línea recta trazando algunos puntos de una ecuación lineal dada. En este capítulo, aprenderemos algunos conceptos importantes de ecuaciones lineales y los usaremos para trazar líneas rectas.

Graficando Ecuaciones Lineales Usando Intercepciones

En la gráfica de una línea recta en el sistema de coordenadas rectangulares, hay dos puntos especiales, el$x$ -intercepto y el$y$ -intercepto.

A partir de la geometría, sabemos que una línea recta está totalmente determinada por dos puntos. Por lo tanto, después de identificar las intercepciones de una ecuación lineal dada, podemos trazar su gráfica utilizando estos dos puntos. Es una buena práctica encontrar un tercer punto. Si el tercer punto no se encuentra en la línea recta determinada por las intercepciones, esto indica que es posible que hayamos cometido un error en nuestros cálculos.

El$x$ -intercept

El$x$ -intercept es el punto donde la gráfica se cruza con el$x$ eje.

Para encontrar la$x$ -intercepción, evalúe la ecuación en$y=0$.

El$x$ -intercepto se verá como$(x$ -intercepción$, 0)$.

El$y$ -intercept

El$y$ -intercept es el punto donde la gráfica se cruza con el$y$ eje.

Para encontrar la$y$ -intercepción, evalúe la ecuación en$x=0$.

El$y$ -intercepto se verá como$(0, y$ -intercepción$)$.

Ejemplo 26.1

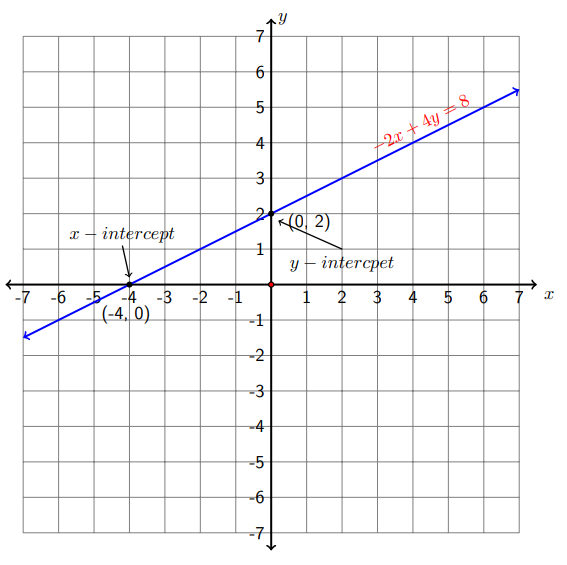
Encuentra las intercepciones de$−2x + 4y = 8$ y utilízalas para graficar la ecuación lineal.

\[\text { Let } y=0 \quad \Rightarrow \quad-2 x+4(0)=8 \quad \Rightarrow \quad-2 x=8 \quad \Longrightarrow \quad x=-4\nonumber\]

Por lo tanto, la$x-$ intercepción es (-4,0).

\[\text { Let } x=0 \quad \Longrightarrow \quad-2(0)+4 y=8 \quad \Longrightarrow \quad 4 y=8 \quad \Rightarrow \quad y=2\nonumber\]

Por lo tanto, la$y-$ intercepción es (0,2)

$clipboard_ee802c408bf243d677d3e256d68d5a142.png$

Ejemplo 26.2

Encuentra las intercepciones de$5x + 2y = 6$ y utilízalas para graficar la ecuación. Primero encontramos las dos intercepciones (y luego encontramos un tercer punto).

\[\text { Let } y=0 \quad \Longrightarrow \quad 5 x+2(0)=6 \quad \Longrightarrow \quad 5 x=6 \quad \Longrightarrow \quad x=\frac{6}{5}=1.2\nonumber\]

\[\text { Let } x=0 \quad \Longrightarrow \quad 5(0)+2 y=6 \quad \Rightarrow \quad 2 y=6 \quad \Rightarrow \quad y=3\nonumber\]

\[\text { Let } x=2 \quad \Longrightarrow \quad 5(2)+2 y=6 \quad \Rightarrow \quad 10+2 y=6 \quad \Rightarrow \quad y=-2\nonumber\]

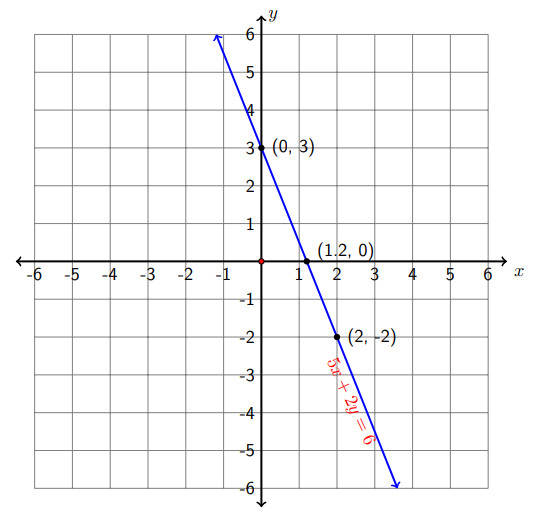
Ahora tenemos tres pares de solución: (1.2,0), (0,3) y$(2,-2) .$ La siguiente figura es la gráfica de la ecuación$5 x+2 y=6$.

$clipboard_e7999302857bed1719dfa66dc23b9b784.png$

La pendiente de una línea

Diferentes líneas rectas tienen diferente pendiente. Matemáticamente, hay un número que puede medir la inclinación de una línea dada. Este número se llama pendiente de una línea, y se denota con la letra$m$. La siguiente figura nos ayuda a determinar la fórmula para calcular la pendiente$m$.

En la siguiente figura,$P$ y$Q$ se encuentran dos puntos arbitrarios en la línea dada. Punto$P$ tiene las coordenadas$\left(x_{1}, y_{1}\right),$ y punto$Q$ tiene las coordenadas$\left(x_{2}, y_{2}\right) .$ Aquí utilizamos subíndices para distinguir coordenadas para diferentes puntos. La pendiente$m$ se define como la relación entre el cambio de los dos puntos en la$y$ dirección y el cambio de los dos puntos en la$x$ dirección.

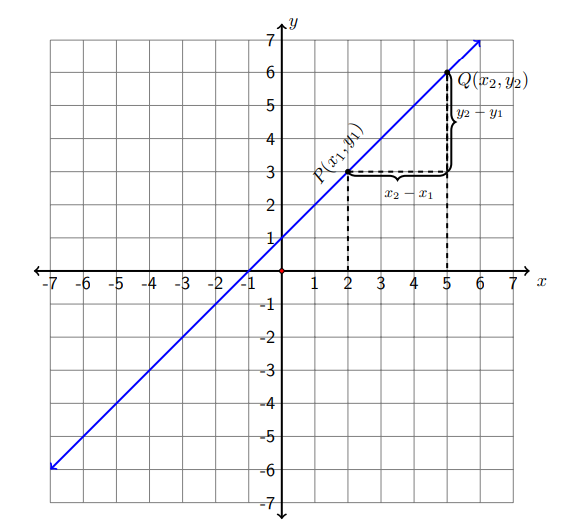
$clipboard_e8d381f2a5299e10bbaf054ed30145b25.png$

ya que la$y$ dirección es vertical, el cambio en$y$ las coordenadas se conoce como la “subida”. De igual manera, la$x$ dirección es horizontal por lo que el cambio en$x$ las coordenadas se conoce como la “carrera”. Entonces otra forma de recordar la fórmula para encontrar la pendiente es recordar que es el “ascenso sobre carrera”.

La pendiente de una línea

La pendiente de una línea que pasa por$\left(x_{1}, y_{1}\right)$ y$\left(x_{2}, y_{2}\right)$ es

\[m=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}=\frac{\text { rise }}{\text { run }}\nonumber\]

Ejemplo 26.3

Encuentra la pendiente de la línea que pasa por los siguientes puntos y usa los puntos dados para graficar la línea.

a) (1,2) y (3,3)

Elegimos$\left(x_{1}, y_{1}\right)=(1,2)$ y$\left(x_{2}, y_{2}\right)=(3,3) .$ en realidad no importa a qué punto asignemos como primer y segundo punto. Siempre obtendremos la misma pendiente.

\[m=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}=\frac{3-2}{3-1}=\frac{1}{2}\nonumber\]

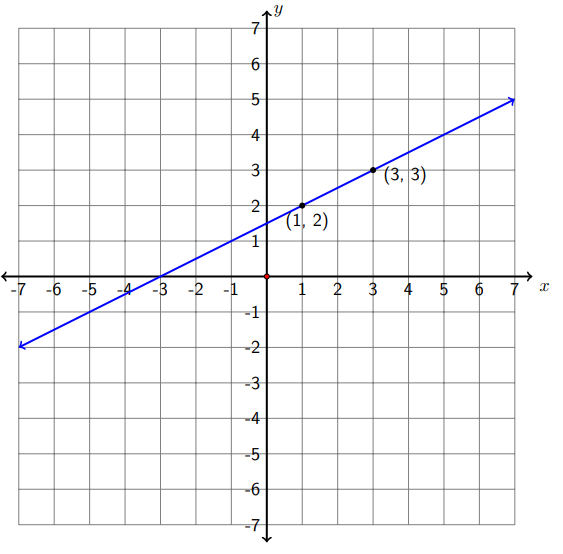
$clipboard_e52fb3f659117497636d66a04f4ba9401.png$

La pendiente es positiva. El gráfico muestra que es una línea ascendente de izquierda a derecha.

b) (-2,4) y (2, -4)

Let$\left(x_{1}, y_{1}\right)=(-2,4)$ y$\left(x_{2}, y_{2}\right)=(2,-4) .$ Entonces

\[m=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}=\frac{-4-4}{2-(-2)}=\frac{-8}{4}=-2\nonumber\]

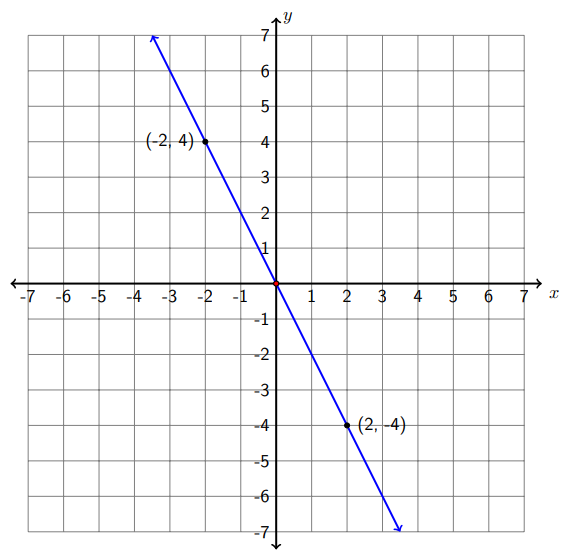
$clipboard_e778cb8e8fe1281f1c21b48dad8083635.png$

La pendiente es negativa. El gráfico muestra que es una línea descendente de izquierda a derecha, y esta línea es más pronunciada que la línea de la parte a).

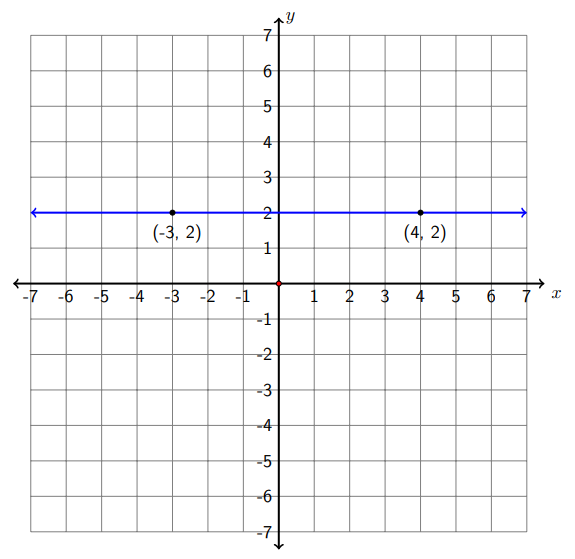
c) (-3,2) y (4,2)

Let$\left(x_{1}, y_{1}\right)=(-3,2)$ y$\left(x_{2}, y_{2}\right)=(4,2) .$ Entonces

\[m=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}=\frac{2-2}{4-(-3)}=\frac{0}{7}=0\nonumber\]

La pendiente es 0. La gráfica muestra que es una línea horizontal.

Nota: Todas las líneas horizontales se caracterizan por puntos que tienen el mismo valor y, por lo que todas tienen una pendiente 0.

$clipboard_ef74d94235f0bebc1c382ee2b61e5e19d.png$

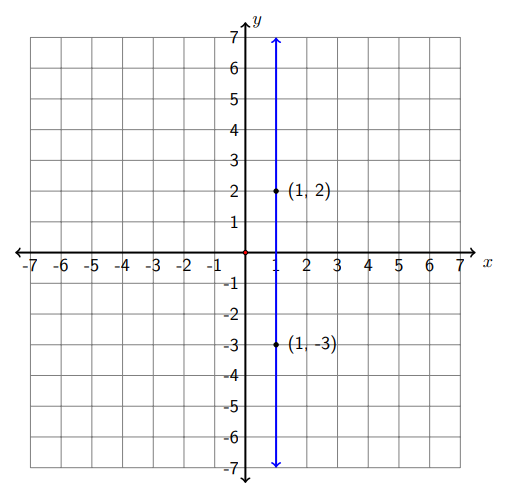
d) (1,2) y (1, -3)

Let$\left(x_{1}, y_{1}\right)=(1,2)$ y$\left(x_{2}, y_{2}\right)=(1,-3) .$ Entonces

\[m=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}=\frac{-3-2}{1-1}=\frac{-5}{0}=\text { undefined }\nonumber\]

La pendiente es indefinida. La gráfica muestra que es una línea vertical.

Nota: Todas las líneas verticales se caracterizan por puntos que tienen el mismo$x$ valor, por lo que todas tienen una pendiente indefinida.

$clipboard_e9de337d8653892e998f7f8f9c61e8ae2.png$

Propiedades de la Talud

Si la pendiente es positiva, la línea va hacia arriba de izquierda a derecha.
Si la pendiente es negativa, las líneas van hacia abajo de izquierda a derecha.
Si la pendiente es$0,$ la línea es horizontal, es decir, no hay subida en la$y$ dirección.
Si la pendiente es indefinida, la línea es vertical, es decir, no hay carrera en la$x$ dirección.
Cuanto mayor sea el valor absoluto de la pendiente, más pronunciada será la línea recta.

Forma de pendiente-intercepción de la ecuación de una línea$\bf{y=m x+b}$

En el apartado anterior, aprendimos que para encontrar la pendiente de una línea, necesitamos dos puntos en la línea. Dada una ecuación de una línea, podemos encontrar fácilmente dos puntos en la línea al encontrar dos pares de solución de la ecuación. Sin embargo, hay otra manera de identificar la pendiente.

Encontremos la pendiente de la línea dada por la ecuación:$2 x-3 y=4$. Podemos elegir dos puntos cualesquiera en la línea, así que vamos a elegir trabajar con las$y$ intercepciones$x$ y.

\[\text { Let } x=0 \quad \Longrightarrow \quad 2(0)-3 y=4 \quad \Longrightarrow \quad-3 y=4 \quad \Longrightarrow \quad y=-\frac{4}{3}\nonumber\]

\[\text { Let } y=0 \quad \Longrightarrow \quad 2 x-3(0)=4 \quad \Longrightarrow \quad 2 x=4 \quad \Longrightarrow \quad x=2\nonumber\]

Por lo tanto las intercepciones son:$\left(0,-\frac{4}{3}\right)$ y (2,0) y así la pendiente es:

\[m=\frac{0-\left(-\frac{4}{3}\right)}{2-0}=\frac{\frac{4}{3}}{2}=\frac{4}{3} \cdot \frac{1}{2}=\frac{2}{3}\nonumber\]

Supongamos que volvemos a nuestra ecuación original y la resolvemos para$y:$

\ [\ begin {alinear*}
2 x-3 y=4 &\ Longrightarrow-3 y=-2 x+4\\
&\ Longrightarrow y=\ frac {-2 x+4} {-3}\\
&\ Longrightarrow y=\ frac {2} {3} x-\ frac {4} {3}
\ end {align*}\ nonumber\]

Reescribir la ecuación de esta manera nos ayuda a identificar dos valores numéricos$\frac{2}{3}$ y$-\frac{4}{3}$. El primer valor es exactamente el mismo que la pendiente y el segundo es exactamente el mismo que el$y$ -intercepto! Esto es cierto en general. Si la ecuación de una línea se escribe en la forma$y=m x+b,$ entonces el coeficiente del$x$ término es la pendiente de la línea y el término constante es la$y$ coordenada -de la$y-$ intercepción (así escribimos$(0, b))$.

La forma pendiente-intercepción de la ecuación de una línea

$y=m x+b$

se llama la forma pendiente-intersección de la ecuación de una línea con pendiente$m$ e$y$ interecpt$(0, b)$.

Ejemplo 26.4

Encuentra la pendiente e$y-$ intercepción de la línea reescribiendo la ecuación de línea$x+4 y=8$ en la forma pendiente-intersección.

\ [\ begin {align*}
x+4 y=8 &\ Longrightarrow 4 y=-x+8\\
&\ Longrightarrow y=\ frac {-x+8} {4}\\
&\ Longrightarrow y=-\ frac {1} {4} x+2
\ end {align*}\ nonumber\]

La pendiente es$-\frac{1}{4}$ y la$y$ -intercepción es (0,2). Recordatorio: La pendiente es un valor numérico. ¡No dejes que la$x$ variable te acompañe cuando la escribas!

Graficar ecuaciones lineales usando la pendiente y la$\bf{y}$ intersección

Usando la$y$ intersección y la pendiente de una línea, podemos esbozar fácilmente la gráfica de una línea recta. Recuerda que solo necesitamos dos puntos para graficar una línea. Usamos el$y$ -intercept como primer punto, luego usamos la pendiente y la$y$ -intercepción para obtener otro punto.

Ejemplo 26.5

Grafique la ecuación lineal dada usando la pendiente y la$y$ intersección:

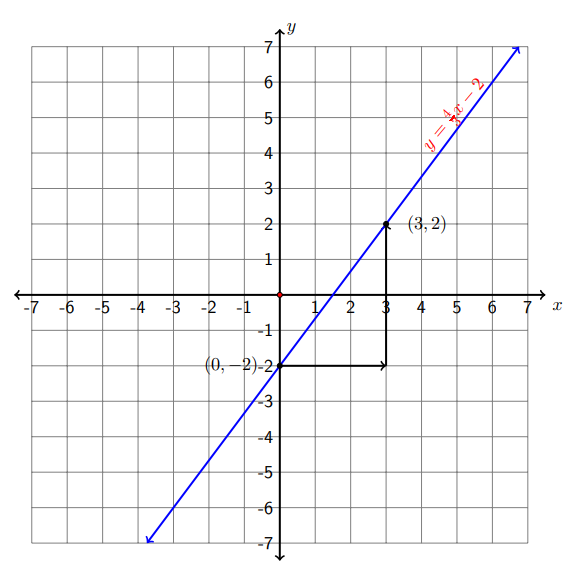
a)$y=\frac{4}{3} x-2$

Paso 1 Escribe la ecuación lineal en la forma pendiente-intercepción. En este problema la ecuación dada ya está en$y=m x+b$ forma, por lo que podemos identificar que la pendiente es$m=\frac{4}{3}$ y la$y-$ intersección es (0, -2).

Paso 2 Trazar la$y-$ intercepción (0, -2) en el$y-$ eje del sistema de coordenadas.

Paso 3 Usa la pendiente$m=\frac{4}{3}=\frac{\text { rise }}{\text { run }}$ para ubicar el segundo punto, es decir, desde la$y$ -intercepción nos movemos hacia la derecha (correr) tres unidades y subir (subir) 4 unidades para trazar un segundo punto en (3,2).

Paso 4 Dibuja una línea pasando por los dos puntos.

$clipboard_e1aebca44de5df4ba3c4c7eee64057df9.png$

b)$x+4 y=8$

Paso 1 Escribe la ecuación lineal en la forma pendiente-intercepción. (Consulte el Ejemplo 26.4 para ver cómo se hace esto):

\[x+4 y=8 \quad \Longrightarrow \quad y=-\frac{1}{4} x+2\nonumber\]

Paso 2 Trazar la$y$ -intercepción (0,2) en el$y$ eje -del sistema de coordenadas.

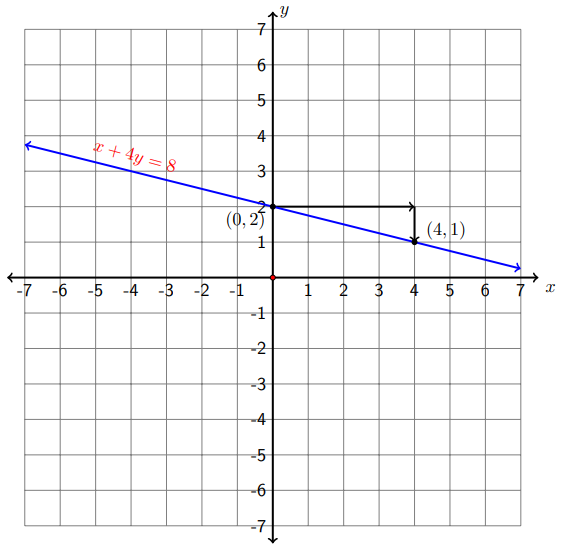
Paso 3 Usando la pendiente$m=-\frac{1}{4}=\frac{-1}{4}=\frac{\text { rise }}{\text { run }}$ para ubicar el segundo punto, es decir, desde la$y$ -intercepción nos movemos hacia la derecha (correr) cuatro unidades y hacia abajo (subir) una unidad (porque el cambio en$y$ es negativo, nos movemos hacia abajo) y trazamos un segundo punto en$(4,1)$.

Aquí optamos por poner el signo negativo en el numerador, pero podríamos haber asignado fácilmente el signo negativo al denominador. Esto se puede hacer porque

\[-\frac{1}{4}=\frac{-1}{4}=\frac{1}{-4}\nonumber\]

Si decidimos trabajar con la pendiente escrita a$m=\frac{1}{-4},$ partir de la$y$ -intercepción (0,2) moveríamos cuatro unidades a la izquierda (carrera) y una unidad$u p$ (subida). Esto nos aterrizaría en ese punto$(-4,3)$.

Paso 4 Dibuja una línea pasando por los dos puntos. Cualesquiera que sean los dos puntos con los que terminemos trabajando ya sea$(0,2)$$(0,2)$ y$(4,1)$ o y$(-4,3)-$ obtenemos la misma línea, ¡pruébalo! La siguiente figura muestra la línea tal como se dibuja a partir de los puntos$(0,2)$ y$(4,1)$.

$clipboard_e728824e8e9963c928fa0f3419df7fadf.png$

c)$2 x-y=0$

Paso 1 Escribe la ecuación lineal en la forma pendiente-intercepción.

\[2 x-y=0 \quad \Longrightarrow \quad-y=-2 x \quad \Longrightarrow \quad y=2 x\nonumber\]

Aquí la pendiente es 2 y la$y-$ intercepción es$(0,0)$.

Paso 2 Trazar la$y$ -intercepción (0,0) en el$y$ eje -que es el origen del sistema de coordenadas.

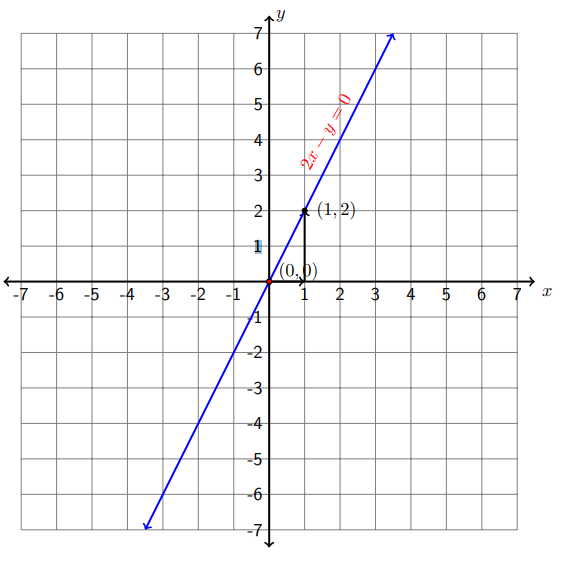
Paso 3 Usando la pendiente$m=2=\frac{2}{1}=\frac{\text { rise }}{\text { run }}$ para ubicar el segundo punto, es decir, desde la$y$ -intercepción nos movemos hacia la derecha (correr) una unidad y subir (subir) dos unidades, trazar un segundo punto en$(1,2)$.

Paso 4 Dibuja una línea que pase por los dos puntos.

$clipboard_e18b0d2da14592c3574af605efd7fbd2a.png$

Forma Punto-Pendiente de la Ecuación de una Línea$y-y_{0}=m\left(x-x_{0}\right)$

Supongamos que se nos da sólo la pendiente de una línea y un punto en la línea y se nos pide encontrar su ecuación. A pesar de que no conocemos la$y$ intersección de inmediato, todavía podemos encontrar la ecuación de la línea usando lo que se llama la fórmula de punto-pendiente (o forma).

La forma punto-pendiente de la ecuación de una línea

\[y-y_{0}=m\left(x-x_{0}\right)\nonumber\]

se llama la forma punto-pendiente de la ecuación de una línea de pendiente$m$ que pasa por el punto$\left(x_{0}, y_{0}\right)$.

Ejemplo 26.6

Encuentra la ecuación de la línea que pasa por el punto (1, -2) con pendiente$\frac{1}{5}$.

Usamos la fórmula de punto-pendiente aquí, con$m=\frac{1}{5}, x_{0}=1$ y$y_{0}=-2$ Entonces, la ecuación de la línea estará dada por$y-(-2)=\frac{1}{5}(x-1)$$y+2=\frac{1}{5} x-\frac{1}{5},$ so$y=\frac{1}{5} x-\frac{1}{5}-2,$ y

\[y=\frac{1}{5} x-\frac{11}{5}\nonumber\]

Nota: La ecuación$y=\frac{1}{5} x-\frac{11}{5}$ está escrita en la forma pendiente-intercepción, por lo tanto podemos leer la$y$ -intercepción si lo deseamos:$\left(0,-\frac{11}{5}\right)$.

Ejemplo 26.7

Encuentra la ecuación de la línea que pasa por los puntos$(3,2)$ y$(-4,3)$.

Observe que aquí no se nos da la pendiente. Tenemos que encontrarlo antes de que podamos proceder a encontrar la ecuación de la línea.

La pendiente es$m=\frac{3-2}{-4-3}=-\frac{1}{7}$.

Ahora, podemos elegir cualquiera de los puntos dados como nuestro punto único y usar la forma de punto-pendiente para encontrar la ecuación de la línea. Vamos a usar$(3,2)$.

Entonces, con$m=-\frac{1}{7}, x_{0}=3$ y$y_{0}=2,$ la ecuación de la línea estará dada por

\[y-2=-\frac{1}{7}(x-3)\nonumber\]

\[y-2=-\frac{1}{7} x+\frac{3}{7}=-\frac{1}{7} x+\frac{3}{7}+2\nonumber\]

y, por último,

\[y=-\frac{1}{7} x+\frac{17}{7}\nonumber\]

Nota: Nuevamente, si queremos leer fuera de la$y-$ intercepción, lo es$\left(0, \frac{17}{7}\right)$.

Ecuaciones de Líneas Horizontales y Verticales

Recordemos que todas las líneas horizontales tienen pendiente$0 .$

Ecuación de una línea horizontal

La ecuación de una línea horizontal que pasa por el punto$(a, b) \text { is } y=b$

Recordemos que todas las líneas verticales tienen una pendiente indefinida.

Ecuación de una línea vertical

La ecuación de una línea vertical que pasa por el punto$(a, b) \text { is } x=a$

Ejemplo 26.8

a) La ecuación de la línea horizontal que pasa por el punto (3, -7) es$y=-7$.

b) La ecuación de la línea vertical que pasa por el punto$\left(\frac{2}{5},-1\right)$ es$x=\frac{2}{5}$.

c) La ecuación de la línea horizontal que pasa por el punto (4,0) es$y=0$.

d) La ecuación de la línea vertical que pasa por el punto$\left(-\frac{1}{2}, 0\right)$ es$x=$$-\frac{1}{2}$.

Problema de salida

Indique la pendiente y la$y$ intersección, y grafique la ecuación:$6 x+4 y=6$