2.8: Desigualdades lineales y desigualdades de valor absoluto
- Page ID
- 116823
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Utilice la notación de intervalos.
- Utilizar las propiedades de las desigualdades.
- Resolver las desigualdades en una variable algebraicamente.
- Resolver desigualdades de valor absoluto.
No es fácil hacer el papel de honor en la mayoría de las universidades de primer nivel. Supongamos que se requería que los estudiantes llevaran una carga de curso de al menos horas de\(12\) crédito y mantuvieran un promedio de calificaciones\(3.5\) igual o superior. ¿Cómo podrían expresarse matemáticamente estos requisitos de lista de honor? En esta sección, exploraremos diversas formas de expresar diferentes conjuntos de números, desigualdades y desigualdades de valor absoluto.

Uso de la notación de intervalos
Indicando la solución a una desigualdad como la que se\(x≥4\) puede lograr de varias maneras.
- Podemos usar una línea numérica como se muestra en la Figura\(\PageIndex{2}\). El rayo azul comienza en\(x = 4\) y, como lo indica la punta de flecha, continúa hasta el infinito, lo que ilustra que el conjunto de soluciones incluye todos los números reales mayores o iguales a\(4\).
- Podemos usar la notación set-builder:\(\{x|x≥4\}\), que se traduce como “todos los números reales\(x\) tales\(x\) que sean mayores o iguales a”\(4\). Observe que las llaves se utilizan para indicar un conjunto.
- El tercer método es la notación de intervalos, en la que los conjuntos de soluciones se indican con paréntesis o corchetes. Las soluciones a\(x≥4\) se representan como\([4,\infty)\). Este es quizás el método más útil, ya que se aplica a conceptos estudiados más adelante en este curso y a otros cursos de matemáticas de nivel superior.

El concepto principal a recordar es que los paréntesis representan soluciones mayores o menores que el número, y los corchetes representan soluciones que son mayores o iguales o menores que o iguales al número. Use paréntesis para representar infinito o infinito negativo, ya que el infinito positivo y negativo no son números en el sentido habitual de la palabra y, por lo tanto, no pueden ser “igualados”. Algunos ejemplos de un intervalo, o un conjunto de números en los que cae una solución, son\([−2,6)\), o todos los números entre\(−2\) y\(6\), incluyendo\(−2\), pero sin incluir\(6\);\((−1,0)\), todos los números reales entre, pero sin incluir\(−1\) y\(0\); y\((−\infty,1]\), todos los reales números menores que e incluyendo\(1\). Tabla\(\PageIndex{1}\) describe las posibilidades.
| Set Indicado | Notación de Set-Builder | Notación de intervalos |
|---|---|---|
| Todos los números reales entre\(a\) y\(b\), pero sin incluir\(a\) o\(b\) | \(\{x|a<x<b\}\) | \((a,b)\) |
| Todos los números reales mayores que\(a\), pero sin incluir\(a\) | \(\{x|x>a\}\) | \((a,\infty)\) |
| Todos los números reales menores que\(b\), pero sin incluir\(b\) | \(\{x|x<b\}\) | \((−\infty,b)\) |
| Todos los números reales mayores que\(a\), incluyendo\(a\) | \(\{x|x≥a\}\) | \([a,\infty)\) |
| Todos los números reales menores que\(b\), incluyendo\(b\) | \(\{x|x≤b\}\) | \((−\infty,b]\) |
| Todos los números reales entre\(a\) y\(b\), incluyendo\(a\) | \(\{x|a≤x<b\}\) | \([a,b)\) |
| Todos los números reales entre\(a\) y\(b\), incluyendo\(b\) | \(\{x|a<x≤b\}\) | \((a,b]\) |
| Todos los números reales entre\(a\) y\(b\), incluyendo\(a\) y\(b\) | \(\{x|a≤x≤b\}\) | \([a,b]\) |
| Todos los números reales menores\(a\) o mayores que\(b\) | \(\{x|x<a\space and\space x>b\}\) | \((−\infty,a)\cup(b,\infty)\) |
| Todos los números reales | \(\{x|x\space is\space all\space real\space numbers\}\) | \((−\infty,\infty)\) |
Utilice la notación de intervalos para indicar todos los números reales mayores o iguales a\(−2\).
Solución
Use un corchete a la izquierda de\(−2\) y paréntesis después del infinito:\([−2,\infty)\). El corchete indica que\(−2\) está incluido en el conjunto con todos los números reales mayores que\(−2\) al infinito.
Utilice la notación de intervalos para indicar todos los números reales entre e incluyendo\(−3\) y\(5\).
- Responder
-
\([−3,5]\)
Escriba el intervalo expresando todos los números reales menores o iguales\(−1\) o mayores que o iguales a\(1\).
Solución
Tenemos que escribir dos intervalos para este ejemplo. El primer intervalo debe indicar todos los números reales menores o iguales a\(1\). Entonces, este intervalo comienza en\(−\infty\) y termina en\(−1\), que se escribe como\((−\infty,−1]\).
El segundo intervalo debe mostrar todos los números reales mayores o iguales a\(1\), que se escribe como\([1,\infty)\). No obstante, queremos combinar estos dos conjuntos. Esto lo conseguimos insertando el símbolo de unión,, entre los dos intervalos.
\[(−\infty,−1]\cup[1,\infty) \nonumber\]
Expresar todos los números reales menores\(−2\) o mayores que o iguales a\(3\) en notación de intervalo.
- Responder
-
\((−\infty,−2)\cup[3,\infty)\)
Uso de las Propiedades de las Desigualdades
Cuando trabajamos con desigualdades, generalmente podemos tratarlas de manera similar pero no exactamente como tratamos las igualdades. Podemos usar la propiedad de suma y la propiedad de multiplicación para ayudarnos a resolverlas. La única excepción es cuando multiplicamos o dividimos por un número negativo; al hacerlo, se invierte el símbolo de desigualdad.
Propiedad de adición
- Si\(a<b\), entonces\(a+c<b+c\).
Propiedad Multiplicación
- Si\(a<b\) y\(c>0\), entonces\(ac<bc\).
- Si\(a<b\) y\(c<0\), entonces\(ac>bc\).
Estas propiedades también se aplican a\(a≤b\),\(a>b\), y\(a≥b\).
Ilustrar la propiedad de adición para las desigualdades resolviendo cada uno de los siguientes:
- (a)\(x−15<4\)
- b)\(6≥x−1\)
- c)\(x+7>9\)
Solución
La propiedad de suma para las desigualdades establece que si existe una desigualdad, sumar o restar el mismo número en ambos lados no cambia la desigualdad.
a.
\[\begin{align*} x-15&< 4\\ x-15+15&< 4+15\\ x&< 19 \end{align*}\]
b.
\[\begin{align*} 6&\geq x-1\\ 6+1&\geq x-1+1\\ 7&\geq x \end{align*}\]
c.
\[\begin{align*} x+7&> 9\\ x+7-7&> 9-7\\ x&> 2 \end{align*}\]
Resolver:\(3x−2<1\).
- Responder
-
\(x<1\)
Ilustrar la propiedad de multiplicación para las desigualdades resolviendo cada una de las siguientes situaciones:
- \(3x<6\)
- \(−2x−1≥5\)
- \(5−x>10\)
Solución
a.
\[\begin{align*} 3x&< 6\\ \dfrac{1}{3}(3x)&< (6)\dfrac{1}{3}\\ x&< 2 \end{align*}\]
b.
\[\begin{align*} -2x-1&\geq 5\\ -2x&\geq 6\\ \left (-\dfrac{1}{2} \right )(-2)&\geq (6)\left (-\dfrac{1}{2} \right ) & & \text{Multiply by } \left (-\dfrac{1}{2} \right )\\ x&\leq -3 & & \text{Reverse the inequality.} \end{align*}\]
c.
\[\begin{align*} 5-x&> 10\\ -x&> 5\\ (-1)(-x)&> (5)(-1) & & \text{Multiply by } -1\\ x&< -5 & & \text{Reverse the inequality.} \end{align*}\]
Resolver:\(4x+7≥2x−3\).
- Responder
-
\(x≥−5\)
Resolver desigualdades en una variable algebraicamente
Como han mostrado los ejemplos, podemos realizar las mismas operaciones en ambos lados de una desigualdad, así como lo hacemos con ecuaciones; combinamos términos similares y realizamos operaciones. Para resolver, aislamos la variable.
Resolver la desigualdad:\(13−7x≥10x−4\).
Solución
Resolver esta desigualdad es similar a resolver una ecuación hasta el último paso.
\[\begin{align*} 13-7x&\geq 10x-4\\ 13-17x&\geq -4 & & \text{Move variable terms to one side of the inequality}\\ -17x&\geq -17 & & \text{Isolate the variable term}\\ x&\leq 1 & & \text{Dividing both sides by -17 reverses the inequality.} \end{align*}\]
El conjunto de soluciones viene dado por el intervalo\((−\infty,1]\), o todos los números reales menores que e incluyendo\(1\).
Resolver la desigualdad y escribir la respuesta usando notación de intervalo:\(−x+4<\dfrac{1}{2}x+1\).
- Responder
-
\((2,\infty)\)
Resuelve la siguiente desigualdad y escribe la respuesta en notación de intervalos:\(−\dfrac{3}{4}x≥−\dfrac{5}{8}+\dfrac{2}{3}x\).
Solución
Comenzamos a resolver de la misma manera que lo hacemos al resolver una ecuación.
\[\begin{align*} -\dfrac{3}{4}x&\geq -\dfrac{5}{8}+\dfrac{2}{3}x\\[5pt] -\dfrac{3}{4}x-\dfrac{2}{3}x&\geq -\dfrac{5}{8} & & \text{Put variable terms on one side.}\\[5pt] -\dfrac{9}{12}x-\dfrac{8}{12}x&\geq -\dfrac{5}{8} & & \text{Write fractions with common denominator.}\\[5pt] -\dfrac{17}{12}x&\geq -\dfrac{5}{8}\\[5pt] x&\leq -\dfrac{5}{8}\left (-\dfrac{12}{17} \right ) & & \text{Multiplying by a negative number reverses the inequality.}\\[5pt] x&\leq \dfrac{15}{34} \end{align*}\]
El conjunto de soluciones es el intervalo\(\left (−\infty,\dfrac{15}{34} \right ]\).
Resolver la desigualdad y escribir la respuesta en notación de intervalos:\(−\dfrac{5}{6}x≤\dfrac{3}{4}+\dfrac{8}{3}x\).
- Responder
-
\(\left [-\dfrac{3}{14},\infty \right )\)
Comprender las desigualdades compuestas
Una desigualdad compuesta incluye dos desigualdades en una sola declaración. Una declaración como\(4<x≤6\) medios\(4<x\) y\(x≤6.\) Hay dos formas de resolver las desigualdades compuestas: separándolas en dos desigualdades separadas o dejando intacta la desigualdad compuesta y realizando operaciones en las tres partes al mismo tiempo. Ilustraremos ambos métodos.
Resolver la desigualdad compuesta:\(3≤2x+2<6\)
Solución
El primer método es escribir dos desigualdades separadas:\(3≤2x+2\) y Las\(2x+2<6.\) resolvemos de forma independiente.
\ [\ begin {array} {lcr}
3≤2x+2 &\ text {y} & 2x+2 <6\\ [5pt]
1≤2x & & 2x<4\\ [5pt]
\ tfrac {1} {2}\ leq x & & x < 2
\ end {array}\ nonumber\]
Entonces, podemos reescribir la solución como una desigualdad compuesta, de la misma manera que comenzó el problema.
\[\frac{1}{2}≤x<2\nonumber\]
En notación de intervalos, la solución se escribe como\([\tfrac{1}{2},\, 2).\)
El segundo método consiste en dejar intacta la desigualdad compuesta, y realizar procedimientos de resolución en las tres partes al mismo tiempo.
\ (\ begin {align*}\ qquad 3&≤2x+2<6\\ [5pt]
1&≤2x<4 & &\ text {Aísle el término variable, y resta} 2\ text {de las tres partes.}\\ [5pt]
\ tfrac {1} {2} &≤x<2 & &\ text {Divide las tres partes por} 2.
\ end {alinear*}\)
Obtenemos la misma solución:\([\tfrac{1}{2},\, 2).\)
Resolver la desigualdad compuesta:\(4<2x−8≤10.\)
- Contestar
-
\(6<x≤9\)o\((6,9]\)
Resolver la desigualdad compuesta con variables en las tres partes:\(3+x>7x−2>5x−10.\)
Solución
Vamos a probar el primer método. Escribe dos desigualdades:
\ [\ begin {array} {ccc} 3+x>7x−2 &\ text {y} & 7x−2>5x−10\\ [5pt]
3>6x−2 & & 2x−2>−10\ [5pt]
5>6x & & 2x>−8\ [5pt]
\ tfrac {5} {6} >x & -4<x\ [5pt pt]
\ end {array}\ nonumber\]
El conjunto de soluciones es\(−4<𝑥<\tfrac{5}{6}\) o en notación de intervalos\(\left(−4,\tfrac{5}{6}\right).\) Observe que cuando escribimos la solución en notación de intervalos, el número menor viene primero. Leemos intervalos de izquierda a derecha, ya que aparecen en una recta numérica. Ver Figura\(\PageIndex{3}\).

Resolver la desigualdad compuesta:\(3y<4−5y<5+3y.\)
- Contestar
-
\(\left(−\tfrac{1}{8},\, \tfrac{1}{2}\right)\)
Resolver desigualdades de valor absoluto
Como sabemos, el valor absoluto de una cantidad es un número positivo o cero. Desde el origen, un punto ubicado en\((−x,\, 0)\) tiene un valor absoluto de\(x,\) ya que está a\(x\) unidades de distancia. Considera el valor absoluto como la distancia de un punto a otro punto. Independientemente de la dirección, positiva o negativa, la distancia entre los dos puntos se representa como un número positivo o cero.
Una desigualdad de valor absoluto es una ecuación de la forma
\[|A|<B,\quad |A|≤B, \quad |A|>B,\quad \text{or} \quad|A|≥B,\nonumber\]
Donde\(A,\) y a veces\(B,\) representa una expresión algebraica dependiente de una variable\(x.\) Resolver la desigualdad significa encontrar el conjunto de todos\(x\) - valores que satisfacen el problema. Por lo general, este conjunto será un intervalo o la unión de dos intervalos e incluirá un rango de valores.
Existen dos enfoques básicos para resolver las desigualdades de valores absolutos: gráfica y algebraica. La ventaja del enfoque gráfico es que podemos leer la solución interpretando las gráficas de dos ecuaciones. La ventaja del enfoque algebraico es que las soluciones son exactas, ya que las soluciones precisas a veces son difíciles de leer a partir de una gráfica.
Supongamos que queremos conocer todos los posibles rendimientos de una inversión si pudiéramos ganar alguna cantidad de dinero dentro de $200 de $600. Podemos resolver algebraicamente para el conjunto de\(x\) - valores tales que la distancia entre\(x\) y\(600\) es menor o igual a\(200.\) Representamos la distancia entre\(x\) y\(600\) como\(| x−600 |,\) y por lo tanto,\(| x−600 |≤200\) o
\ [\ begin {array} {c} −200≤x−600≤200\\
−200+600≤x−600+600≤200+600\\
400≤x≤800
\ end {array}\ nonumber\]
Esto significa que nuestras devoluciones estarían entre $400 y $800.
Para resolver las desigualdades de valor absoluto, al igual que con las ecuaciones de valor absoluto, escribimos dos desigualdades y luego las resolvemos de forma independiente.
Para una expresión algebraica\(X\) y\(k>0,\) un valor absoluto la desigualdad es una desigualdad de la forma
\ [\ begin {align*} | X |&<k\ text {es equivalente a} −k<x<k\\ [4pt]
| X |&>k\ text {es equivalente a} x<−k\ text {o} x>k\ end {align*}\]
Estas declaraciones también se aplican a\(| X |≤k\) y\(| X |≥k.\)
Describir todos los valores a una\(x\)\(4\) distancia del número\(5.\)
Solución
Queremos que la distancia entre\(x\) y\(5\) sea menor o igual a\(4.\) Podemos trazar una recta numérica, como en Figura\(\PageIndex{4},\) para representar la condición a satisfacer.

La distancia de\(x\) a se\(5\) puede representar usando un símbolo de valor absoluto,\(| x−5 |.\) Escribe los valores de\(x\) que satisfagan la condición como una desigualdad de valor absoluto.
\[| x−5 |≤4\nonumber\]
Necesitamos escribir dos desigualdades ya que siempre hay dos soluciones a una ecuación de valor absoluto.
\ [\ begin {array} {ccc} x−5≤4 &\ text {y} & x−5≥−4\\ [4pt]
x≤9 & & x≥1
\ end {array}\ nonumber\]
Si el conjunto de soluciones es\(x≤9\) y\(x≥1,\) entonces el conjunto de soluciones es un intervalo que incluye todos los números reales entre e incluyendo 1 y 9.
Entonces\(| x−5 |≤4\) es equivalente a\([ 1,9 ]\) en notación de intervalos.
Describir todos\(x\) los valores dentro de una\(3\) distancia del número\(2.\)
- Contestar
-
\(|x−2|≤3\)
Resolver\(|x−1|≤3.\)
Solución
\ (\ quad\ begin {array} {c} |x−1 |≤3\\ [4pt]
−3≤x−1≤3\\ [4pt]
−2≤x≤4\\ [4pt]
[−2,4]
\ end {array}\)
Dada la ecuación\(y=−\tfrac{1}{2}|4x−5|+3,\) determinar los\(x\) -valores para los cuales los\(y\) -valores son negativos.
Solución
Estamos tratando de determinar donde\(y<0,\) cual es cuando\(−\tfrac{1}{2}|4x−5|+3<0.\) Comenzamos aislando el valor absoluto.
\ [\ begin {align*} −\ tfrac {1} {2} |4x−5|&<−3 & &\ text {Multiplica ambos lados por} —2,\ text {e invierte la desigualdad.}\\ [5pt]
|4x−5|&>6\ end {align*}\]
A continuación, resolvemos por la igualdad\(|4x−5|=6.\)
\ [\ begin {array} {rcr} 4x−5=6 & & 4x−5=−6\\ [5pt]
4x=11 &\ text {o} & 4x=−1\\ [5pt]
x=\ tfrac {11} {4} & & x=−\ tfrac {1} {4}
\ end {array}\ nonumber\]
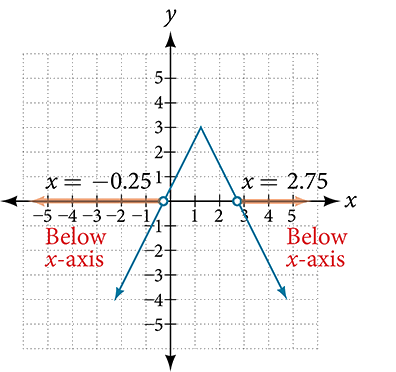
Ahora, podemos examinar la gráfica para observar dónde los\(y\) valores -son negativos. Observamos dónde están las ramas por debajo del\(x\) eje. Observe que no es importante exactamente cómo se ve la gráfica, siempre y cuando sepamos que cruza el eje horizontal en\(x=−\tfrac{1}{4}\) y\(x=\tfrac{11}{4},\) y que la gráfica se abre hacia abajo. Ver Figura\(\PageIndex{5}.\)
Resolver\(−2|k−4|≤−6.\)
- Contestar
-
\(k≤1\)o\(k≥7;\) en notación de intervalos, esto sería\((−∞,1]∪[7,∞).\)
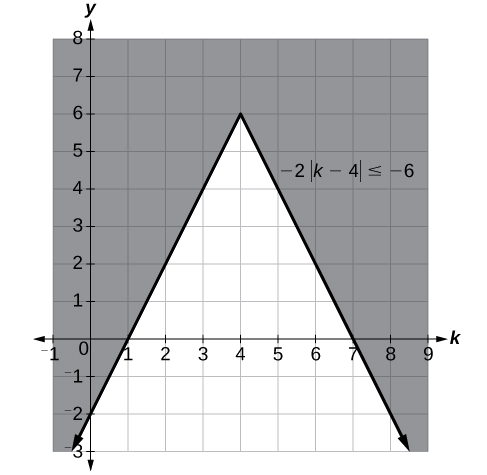
Figura\(\PageIndex{6}\)


