2.7: Otros tipos de ecuaciones
- Page ID
- 116835
- Resolver ecuaciones que involucran exponentes racionales.
- Resolver ecuaciones mediante factorización.
- Resolver ecuaciones radicales.
- Resolver ecuaciones de valor absoluto.
- Resolver otros tipos de ecuaciones.
Hemos resuelto ecuaciones lineales, ecuaciones racionales y ecuaciones cuadráticas usando varios métodos. Sin embargo, hay muchos otros tipos de ecuaciones, e investigaremos algunos tipos más en esta sección. Veremos ecuaciones que involucran exponentes racionales, ecuaciones polinómicas, ecuaciones radicales, ecuaciones de valor absoluto, ecuaciones en forma cuadrática y algunas ecuaciones racionales que pueden transformarse en cuadráticas. Resolver cualquier ecuación, sin embargo, emplea las mismas reglas algebraicas básicas. Aprenderemos algunas técnicas nuevas a medida que se aplican a ciertas ecuaciones, pero el álgebra nunca cambia.
Resolver ecuaciones que involucran exponentes racionales
Los exponentes racionales son exponentes que son fracciones, donde el numerador es una potencia y el denominador es una raíz. Por ejemplo,\({16}^{\tfrac{1}{2}}\) es otra forma de escribir\(\sqrt{16}\);\(8^{\tfrac{1}{3}}\) es otra forma de escribir\(\sqrt[3]{8}\). La capacidad de trabajar con exponentes racionales es una habilidad útil, ya que es altamente aplicable en el cálculo.
Podemos resolver ecuaciones en las que una variable se eleva a un exponente racional elevando ambos lados de la ecuación al recíproco del exponente. La razón por la que elevamos la ecuación al recíproco del exponente es porque queremos eliminar al exponente en el término variable, y un número multiplicado por sus iguales recíprocos\(1\). Por ejemplo,
\[\dfrac{2}{3}\left (\dfrac{3}{2} \right )=1 \nonumber\]
\[3\left (\dfrac{1}{3} \right )=1, \nonumber\]
y así sucesivamente.
Un exponente racional indica una potencia en el numerador y una raíz en el denominador. Hay múltiples formas de escribir una expresión, una variable o un número con un exponente racional:
\[a^{\tfrac{m}{n}}={\left (a^{\tfrac{1}{n}} \right )}^m={a^m}^{\tfrac{1}{n}}=\sqrt[n]{a^m}={(\sqrt[n]{a})}^m\]
Evaluar\(8^{\tfrac{2}{3}}\)
Solución
Si tomamos la raíz primero o la potencia primero depende del número. Es fácil encontrar la raíz cubo de\(8\), así que reescribe\(8^{\tfrac{2}{3}}\) como\({\left (8^{\tfrac{1}{3}} \right )}^2\).
\[\begin{align*} {\left (8^{\tfrac{1}{3}} \right )}^2&= {(2)}^2\\ &= 4 \end{align*}\]
Evaluar\({64}^{-\tfrac{1}{3}}\)
- Responder
-
\(\dfrac{1}{4}\)
Resolver la ecuación en la que una variable se eleva a un exponente racional:\(x^{\tfrac{5}{4}} = 32\).
Solución
La manera de eliminar el exponente en\(x\) es elevando ambos lados de la ecuación a un poder que es el recíproco de\(\dfrac{5}{4}\), que es\(\dfrac{4}{5}\).
\[\begin{align*} x^{\tfrac{5}{4}}&= 32\\ {\left(x^{\tfrac{5}{4}}\right)}^{\tfrac{4}{5}}&= {\left(32\right)}^{\tfrac{4}{5}}\\ x&= (2)^4\\ &= 16 \end{align*}\]
Resuelve la ecuación\(x^{\tfrac{3}{2}} = 125\).
- Responder
-
\(25\)
Resolver\(3x^{\tfrac{3}{4}} = x^{\tfrac{1}{2}}\).
Solución
Esta ecuación implica exponentes racionales así como factorizar exponentes racionales. Demos esto paso a paso. Primero, ponga los términos variables en un lado del signo igual y establezca la ecuación igual a cero.
\[\begin{align*} 3x^{\tfrac{3}{4}}-\left(x^{\tfrac{1}{2}}\right)&= x^{\tfrac{1}{2}}-\left(x^{\tfrac{1}{2}}\right)\\ 3x^{\tfrac{3}{4}}-x^{\tfrac{1}{2}}&= 0 \end{align*}\]
Ahora bien, parece que deberíamos factorizar el lado izquierdo, pero ¿qué factorizamos? Siempre podemos factorizar el término con el exponente más bajo. Reescribir\(x^{\tfrac{1}{2}}\) como\(x^{\tfrac{2}{4}}\). Entonces, factorizar\(x^{\tfrac{2}{4}}\) de ambos términos a la izquierda.
\[\begin{align*} 3x^{\tfrac{3}{4}}-x^{\tfrac{1}{2}}&= 0\\ x^{\tfrac{2}{4}}\left (3x^{\tfrac{1}{4}}-1 \right )&= 0 \end{align*}\]
¿De\(x^{\tfrac{1}{4}}\) dónde vino? Recuerda, cuando multiplicamos dos números con la misma base, sumamos los exponentes. Por lo tanto, si multiplicamos de\(x^{\tfrac{2}{4}}\) nuevo en el uso de la propiedad distributiva, obtenemos la expresión que teníamos antes del factoring, que es lo que debería suceder. Necesitamos un exponente tal que cuando se añada a\(\dfrac{2}{4}\) iguales\(\dfrac{3}{4}\). Así, el exponente encendido\(x\) entre paréntesis es\(\dfrac{1}{4}\).
Sigamos. Ahora tenemos dos factores y podemos usar el teorema del factor cero.
\ [\ begin {alinear*}
x^ {\ tfrac {2} {4}}\ izquierda (3x^ {\ tfrac {1} {4}} -1\ derecha) &= 0\\
x^ {\ tfrac {2} {4}} &= 0\\ x&= 0\ 3x^ {\ tfrac {1} {4}}
-1&= 0\
3x^ {\ tfrac {1} {4}} -1&= 0\
3x^ {\ tfrac {1} {4}} ^ {\ tfrac {1} {4}} &= 1\\
x^ {\ tfrac {1} {4}} &=\ dfrac {1} {3},\ qquad\ texto {Divide ambos lados por 3.} \\
{\ izquierda (x^ {\ tfrac {1} {4}}\ derecha)} ^4&= {\ izquierda (\ dfrac {1} {3}\ derecha)} ^4,\ qquad\ text {Elevar ambos lados al recíproco de}\ dfrac {1} {4}\
x&=\ dfrac {1} {81}
\ end {align*}\]
Las dos soluciones son\(0\) y\(\dfrac{1}{81}\).
Resolver:\({\left(x+5\right)}^{\tfrac{3}{2}}=8\).
- Responder
-
\(-1\)
Resolver ecuaciones usando factorización
Hemos utilizado la factorización para resolver ecuaciones cuadráticas, pero es una técnica que podemos usar con muchos tipos de ecuaciones polinómicas, que son ecuaciones que contienen una cadena de términos incluyendo coeficientes numéricos y variables. Cuando nos enfrentamos a una ecuación que contiene polinomios de grado superior a\(2\), a menudo podemos resolverlos factorizando.
Un polinomio de grado\(n\) es una expresión del tipo
\[a_nx^n+a_{n−1}x^{n−1}+⋅⋅⋅+a_2x^2+a_1x+a_0\]
donde\(n\) is a positive integer and \(a_n ,…, a_0\) are real numbers and \(a_n≠0\).
Establecer el polinomio igual a cero da una ecuación polinómica. El número total de soluciones (reales y complejas) a una ecuación polinómica es igual al exponente más alto\(n\).
Resolver el polinomio factorizando:\(5x^4 = 80x^2\).
Solución
Primero, establezca la ecuación igual a cero. Entonces factorizar lo que es común a ambos términos, el GCF.
\[\begin{align*} 5x^4-80x^2&= 0\\ 5x^2(x^2-16)&= 0 \end{align*}\]
Observe que tenemos la diferencia de cuadrados en el factor\(x^2−16\), que seguiremos factorizando y obteniendo dos soluciones. El primer término,\(5x^2\), genera, técnicamente, dos soluciones como es el exponente\(2\), pero son la misma solución.
\[\begin{align*} 5x^2&= 0\\ x&=0\\ x^2-16&= 0\\ (x+4)(x-4)&= 0\\ x&= 4\\ x&= -4 \end{align*}\]
Las soluciones son\(0\) (solución doble),\(4\), y\(−4\).
Análisis
Podemos ver las soluciones en la gráfica de la Figura\(\PageIndex{1}\). Las coordenadas x de los puntos donde la gráfica cruza el\(x\) eje -son las soluciones, las\(x\) -intercepciones. Observe en la gráfica que en la solución\(0\), la gráfica toca el\(x\) eje -y rebota hacia atrás. No cruza el\(x\) eje -eje. Esto es típico de las soluciones dobles.
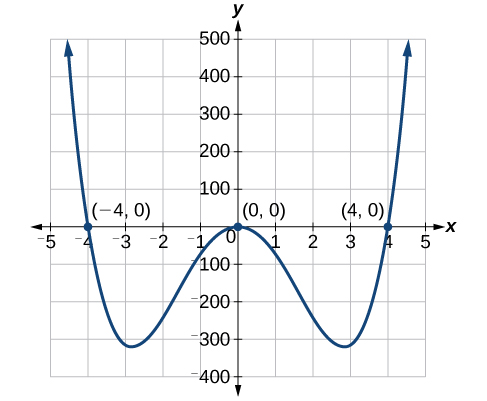
Resolver factorizando:\(12x^4 = 3x^2\).
- Responder
-
\(x=0, x=12, x=−12\)
Resolver un polinomio agrupando:\(x^3+x^2−9x−9=0\).
Solución
Este polinomio consiste en\(4\) términos, que podemos resolver agrupando. Los procedimientos de agrupación requieren factorizar los dos primeros términos y luego factorizar los dos últimos términos. Si los factores entre paréntesis son idénticos, podemos continuar el proceso y resolverlo, a menos que se sugiera más factorización.
\[\begin{align*} x^3+x^2-9x-9&= 0\\ x^2(x+1)-9(x+1)&= 0\\ (x^2-9)(x+1)&= 0 \end{align*}\]
El proceso de agrupación termina aquí, ya que podemos factorizar\(x^2−9\) usando la fórmula de diferencia de cuadrados.
\[\begin{align*} (x^2-9)(x+1)&= 0\\ (x-3)(x+3)(x+1)&= 0\\ x&= 3\\ x&= -3\\ x&= -1 \end{align*}\]
Las soluciones son\(3\),\(−3\), y\(−1\). Tenga en cuenta que el exponente más alto es\(3\) y obtuvimos\(3\) soluciones. Podemos ver las soluciones, las intercepciones x, en la gráfica de la Figura\(\PageIndex{2}\).
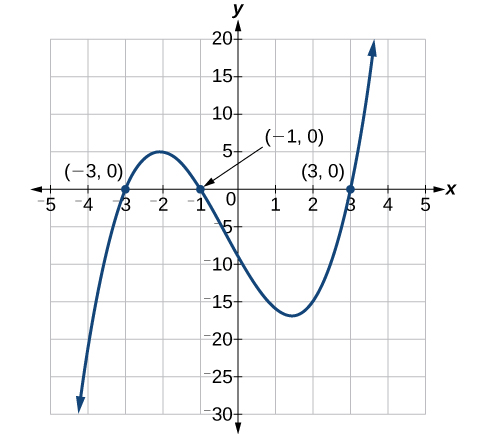
Análisis
Nos fijamos en resolver ecuaciones cuadráticas factorizando cuando el coeficiente principal es\(1\). Cuando el coeficiente principal no lo es\(1\), lo resolvimos agrupando. Agrupar requiere cuatro términos, los cuales obtuvimos dividiendo el término lineal de ecuaciones cuadráticas. También podemos usar agrupación para algunos polinomios de grado superior a\(2\), como vimos aquí, ya que ya había cuatro términos.
Resolviendo ecuaciones radicales
Las ecuaciones radicales son ecuaciones que contienen variables en el radicando (la expresión bajo un símbolo radical), como
\[\sqrt{3x+18}=x \nonumber\]
\[\sqrt{x+3}=x-3 \nonumber\]
\[\sqrt{x+5}-\sqrt{x-3}=2 \nonumber\]
Las ecuaciones radicales pueden tener uno o más términos radicales, y se resuelven eliminando cada radical, uno a la vez. Tenemos que tener cuidado a la hora de resolver ecuaciones radicales, ya que no es raro encontrar soluciones extrañas, raíces que no son, de hecho, soluciones a la ecuación. Estas soluciones no se deben a un error en el método de resolución, sino que resultan del proceso de elevar ambos lados de una ecuación a una potencia. Sin embargo, verificar cada respuesta en la ecuación original confirmará las verdaderas soluciones.
Una ecuación que contiene términos con una variable en el radicando se denomina ecuación radical.
- Aísle la expresión radical en un lado del signo igual. Poner todos los términos restantes en el otro lado.
- Si el radical es una raíz cuadrada, entonces cuadrar ambos lados de la ecuación. Si es una raíz cubo, entonces elevar ambos lados de la ecuación a la tercera potencia. En otras palabras, para un radical\(n^{th}\) raíz, elevar ambos lados al\(n^{th}\) poder. Hacerlo elimina el símbolo radical.
- Resuelve la ecuación restante.
- Si aún queda un término radical, repita los pasos 1—2.
- Confirme las soluciones sustituyéndolas en la ecuación original.
Resolver\(\sqrt{15−2x}=x\).
Solución
El radical ya está aislado en el lado izquierdo del lado igual, así que procede a cuadrar ambos lados.
\[\begin{align*} \sqrt{15-2x}&= x\\ {\left (\sqrt{15-2x} \right )}^2&= {(x)}^2\\ 15-2x&= x^2 \end{align*}\]
Vemos que la ecuación restante es cuadrática. Ponlo igual a cero y resuelve.
\[\begin{align*} 0&= x^2+2x-15\\ 0&= (x+5)(x-3)\\ x&= -5\\ x&= 3 \end{align*}\]
Las soluciones propuestas son\(−5\) y\(3\). Comprobaremos cada solución de nuevo en la ecuación original. Primero, revisa\(x=−5\).
\[\begin{align*} \sqrt{15-2x}&= x\\ \sqrt{15-2(-5)}&=-5\\ \sqrt{25}&= -5\\ 5&\neq -5 \end{align*}\]
Esta es una solución ajena. Si bien no se cometió ningún error al resolver la ecuación, encontramos una solución que no satisface la ecuación original.
Cheque\(x=3\).
\[\begin{align*} \sqrt{15-2x}&= x\\ \sqrt{15-2(3)}&= 3\\ \sqrt{9}&= 3\\ 3&= 3 \end{align*}\]
La solución es\(3\).
Resuelve la ecuación radical:\(\sqrt{x+3}=3x-1\)
- Responder
-
\(x=1\), solución ajena\(x=−\dfrac{2}{9}\)
Resolver\(\sqrt{2x+3}+\sqrt{x-2}=4\)
Solución
Como esta ecuación contiene dos radicales, aislamos un radical, lo eliminamos y luego aislamos al segundo radical.
\[\sqrt{2x+3}+\sqrt{x-2}=4 \nonumber\]
\[\begin{align*} \sqrt{2x+3}&= 4-\sqrt{x-2} \qquad \text{Subtract } \sqrt{x-2} \text{ from both sides}\\ {\left (\sqrt{2x+3} \right )}^2&= {\left (4-\sqrt{x-2} \right )}^2\qquad \text{Square both sides} \end{align*}\]
Usa la fórmula cuadrada perfecta para expandir el lado derecho:\({(a−b)}^2=a^2−2ab+b^2\).
\[\begin{align*} 2x+3&= {(4)}^2-2(4)\sqrt{x-2}+{(\sqrt{x-2})}^2\\ 2x+3&= 16-8\sqrt{x-2}+(x-2)\\ 2x+3&= 14+x-8\sqrt{x-2} \qquad \text{Combine like terms}\\ x-11&= -8\sqrt{x-2} \qquad \text{Isolate the second radical}\\ {(x-11)}^2&= {(-8\sqrt{x-2})}^2 \qquad \text{Square both sides}\\ x^2-22x+121&= 64(x-2) \end{align*}\]
Ahora que ambos radicales han sido eliminados, establecer la cuadrática igual a cero y resolver.
\[\begin{align*} x^2-22x+121&= 64x-128\\ x^2-86x+249&= 0\\ (x-3)(x-83)&= 0\\ x&= 3\\ x&= 83 \end{align*}\]
Las soluciones propuestas son\(3\) y\(83\). Verifique cada solución en la ecuación original.
\[\begin{align*} \sqrt{2x+3}+\sqrt{x-2}&= 4\\ \sqrt{2x+3}&= 4-\sqrt{x-2}\\ \sqrt{2(3)+3}&= 4-\sqrt{(3)-2}\\ \sqrt{9}&= 4-\sqrt{1}\\ 3&= 3 \end{align*}\]
Una solución es\(3\).
Cheque\(x=83\).
\[\begin{align*} \sqrt{2x+3}+\sqrt{x-2}&= 4\\ \sqrt{2x+3}&= 4-\sqrt{x-2}\\ \sqrt{2(83)+3}&= 4-\sqrt{(83)-2}\\ \sqrt{169}&= 4-\sqrt{81}\\ 13&\neq -5 \end{align*}\]
La única solución es\(3\). Vemos que\(x=83\) es una solución ajena.
Resuelve la ecuación con dos radicales:\(\sqrt{3x+7}+\sqrt{x+2}=1\)
- Responder
-
\(x=−2\), solución ajena\(x=−1\)
Resolver una ecuación de valor absoluto
A continuación, aprenderemos a resolver una ecuación de valor absoluto. Para resolver una ecuación como\(|2x−6|=8\), notamos que el valor absoluto será igual a\(8\) si la cantidad dentro de las barras de valor absoluto es\(8\) o\(−8\). Esto lleva a dos ecuaciones diferentes que podemos resolver de forma independiente.
\[\begin{align*} 2x-6&= 8\\ 2x&= 14\\ x&= 7 \end{align*}\]
O
\[\begin{align*} 2x-6&= -8\\ 2x&= -2\\ x&= -1 \end{align*}\]
Saber resolver problemas que involucran funciones de valor absoluto es útil. Por ejemplo, es posible que necesitemos identificar números o puntos en una línea que estén a una distancia especificada de un punto de referencia dado.
El valor absoluto de\(x\) se escribe como\(|x|\). Cuenta con las siguientes propiedades:
Si\(x≥0\), entonces\(|x|=x\) .If\(x<0\), entonces\(x=−x\).
Para números reales\(A\) y\(B\), una ecuación de la forma\(|A|=B\), con\(B≥0\), tendrá soluciones cuando\(A=B\) o\(A=−B\). Si\(B<0\), la ecuación no\(|A|=B\) tiene solución.
Una ecuación de valor absoluto en la forma\(|ax+b|=c\) tiene las siguientes propiedades:
- Si\(c<0\), no\(|ax+b|=c\) tiene solución.
- Si\(c=0\),\(|ax+b|=c\) tiene una solución.
- Si\(c>0\),\(|ax+b|=c\) tiene dos soluciones.
Dada una ecuación de valor absoluto, resolverla.
- Aísle la expresión de valor absoluto en un lado del signo igual.
- Si\(c>0\), escribe y resuelve dos ecuaciones:\(ax+b=c\) y\(ax+b=−c\).
Resuelve las siguientes ecuaciones de valor absoluto:
- \(|6x+4|=8\)
- \(|3x+4|=−9\)
- \(|3x−5|−4=6\)
- \(|−5x+10|=0\)
Solución
- \(|6x+4|=8\)
Escribe dos ecuaciones y resuelve cada una:
\[\begin{align*} 6x+4&= 8\\ 6x&= 4\\ x&= \dfrac{2}{3} \end{align*}\]
O
\[\begin{align*} 6x+4&= -8\\ 6x&= -12\\ x&= -2 \end{align*}\]
Las dos soluciones son\(\dfrac{2}{3}\) y\(−2\).
- \(|3x+4|=−9\)
No hay solución ya que un valor absoluto no puede ser negativo.
- \(|3x−5|−4=6\)
Aísle la expresión de valor absoluto y luego escriba dos ecuaciones.
\[\begin{align*} |3x-5|-4&= 6\\ |3x-5|&= 10\\ 3x-5&= 10\\ 3x&= 15\\ x&= 5 \end{align*}\]
O
\[\begin{align*} 3x-5&= -10\\ 3x=-5\\ x=\dfrac{5}{3} \end{align*}\]
Hay dos soluciones:\(5\), y\(-\dfrac{5}{3}\).
- \(|−5x+10|=0\)
La ecuación se establece igual a cero, así que tenemos que escribir solo una ecuación.
\[\begin{align*} -5x+10&= 0\\ -5x&= -10\\ x&= 2 \end{align*}\]
Hay una solución:\ (2\).
Resolver la ecuación del valor absoluto:\(|1−4x|+8=13\).
- Responder
-
\(x=−1, x=\dfrac{3}{2}\)
Resolver otros tipos de ecuaciones
Hay muchos otros tipos de ecuaciones además de las que hemos discutido hasta ahora. Veremos más de ellos a lo largo del texto. Aquí, discutiremos ecuaciones que están en forma cuadrática, y ecuaciones racionales que resultan en una cuadrática.
Resolver ecuaciones en forma cuadrática
Las ecuaciones en forma cuadrática son ecuaciones con tres términos. El primer término tiene un poder distinto al\(2\). El término medio tiene un exponente que es la mitad del exponente del término principal. El tercer término es una constante. Podemos resolver ecuaciones de esta forma como si fueran cuadráticas. Algunos ejemplos de estas ecuaciones incluyen\(x^4−5x^2+4=0\),\(x^6+7x^3−8=0\), y\(x^{\tfrac{2}{3}} +4x^{\tfrac{1}{3}}+2=0\). En cada uno, duplicar el exponente del término medio equivale al exponente en el término principal. Podemos resolver estas ecuaciones sustituyendo una variable por el término medio.
Si el exponente en el término medio es la mitad del exponente en el término principal, tenemos una ecuación en forma cuadrática, que podemos resolver como si se tratara de una cuadrática. Sustituimos una variable por el término medio para resolver ecuaciones en forma cuadrática.
- Identificar el exponente en el término principal y determinar si es el doble del exponente en el término medio.
- Si es así, sustituya una variable, como\(u\), por la porción variable del término medio.
- Reescribe la ecuación para que tome la forma estándar de una cuadrática.
- Resuelve usando uno de los métodos habituales para resolver una cuadrática.
- Reemplazar la variable de sustitución por el término original.
- Resuelve la ecuación restante.
Resolver esta ecuación de cuarto grado:\(3x^4−2x^2−1=0\).
Solución
Esta ecuación se ajusta a los criterios principales, que la potencia en el término principal es el doble de la potencia en el término medio. A continuación, haremos una sustitución por el término variable en el medio. Vamos\(u =x^2\). Reescribe la ecuación en\(u\).
\[3u^2−2u−1=0 \nonumber\]
Ahora resuelve la cuadrática.
\[\begin{align*} 3u^2-2u-1&= 0\\ (3u+1)(u-1)&= 0 \end{align*}\]
Resuelve cada factor y reemplaza el término original para\(u\).
\[\begin{align*} 3u+1&= 0\\ 3u&= -1\\ u&= -\dfrac{1}{3}\\ x^2&= -\dfrac{1}{3}\\ x&= \pm i\sqrt{\dfrac{1}{3}}\\ u-1&= 0\\ u&= 1\\ x^2&= 1\\ x&= \pm 1 \end{align*}\]
Las soluciones son\(x=±i\sqrt{\dfrac{1}{3}}\) y\(x=±1\)
Resolver usando sustitución:\(x^4−8x^2−9=0\).
- Responder
-
\(x=−3,3,−i,i\)
Resolver la ecuación en forma cuadrática:\({(x+2)}^2+11(x+2)−12=0\).
Solución
Esta ecuación contiene un binomio en lugar de la variable única. La tendencia es ampliar lo que se presenta. Sin embargo, reconocer que se ajusta a los criterios para estar en forma cuadrática marca toda la diferencia en el proceso de resolución. Primero, hacer una sustitución, dejando\(u =x+2\). Después reescribe la ecuación en\(u\).
\[\begin{align*} u^2+11u-12&= 0\\ (u+12)(u-1)&= 0 \end{align*}\]
Resuelva usando la propiedad de factor cero y luego reemplace\(u\) con la expresión original.
\[\begin{align*} u+12&= 0\\ u&= -12\\ x+2&= -12\\ x&= -14 \end{align*}\]
El segundo factor da como resultado
\[\begin{align*} u-1&= 0\\ u&= 1\\ x+2&= 1\\ x&= -1 \end{align*}\]
Tenemos dos soluciones:\(−14\), y\(−1\).
Resolver:\({(x−5)}^2−4(x−5)−21=0\).
- Responder
-
\(x=2,x=12\)
Resolver ecuaciones racionales dando como resultado una cuadrática
Anteriormente, resolvimos ecuaciones racionales. A veces, resolver una ecuación racional resulta en una cuadrática. Cuando esto sucede, continuamos la solución simplificando la ecuación cuadrática por uno de los métodos que hemos visto. Puede resultar que no hay solución.
Resuelve la siguiente ecuación racional:\(\dfrac{-4x}{x-1}+\dfrac{4}{x+1}=\dfrac{-8}{x^2-1}\)
Solución
Queremos que todos los denominadores en forma factorizada encuentren el LCD. Dos de los denominadores no pueden ser factorizados más. Sin embargo,\(x^2−1=(x+1)(x−1)\). Entonces, el LCD es\((x+1)(x−1)\). A continuación, multiplicamos toda la ecuación por la LCD.
\ [\ begin {alinear*} (x+1) (x-1)\ izquierda (\ dfrac {-4x} {x-1} +\ dfrac {4} {x+1}\ derecha) &=\ izquierda (\ dfrac {-8} {x^2-1}\ derecha) (x+1) (x-1)\ -4x (x+1) +4 (x-1) &= -8\ -4x^2-4x+4x-4&= -8\\ -4x^2+4&= 0\\
-4 (x^2-1) &= 0\\ -4 (x+1) (x-1) &= 0\\ x&= -1\\ x&= 1\ end {alinear*}\]
En este caso, cualquiera de las soluciones produce un cero en el denominador en la ecuación original. Por lo tanto, no hay solución.
Resolver\(\dfrac{3x+2}{x-2}+\dfrac{1}{x}=\dfrac{-2}{x^2-2x}\)
- Responder
-
\(x=−1, x= 0\)no es una solución.
Acceda a estos recursos en línea para obtener instrucción adicional y práctica con diferentes tipos de ecuaciones.
- Ecuación racional sin solución
- Resolver ecuaciones con exponentes racionales usando potencias recíprocas
- Resolviendo ecuaciones radicales parte 1 de 2
- Resolviendo ecuaciones radicales parte 2 de 2
Conceptos clave
- Los exponentes racionales se pueden reescribir de varias maneras dependiendo de lo que sea más conveniente para el problema. Para resolver, ambos lados de la ecuación se elevan a una potencia que hará que el exponente en la variable sea igual a\(1\). Ver Ejemplo, Ejemplo y Ejemplo.
- La factorización se extiende a polinomios de orden superior cuando implica factorizar el GCF o factorizar por agrupación. Ver Ejemplo y Ejemplo.
- Podemos resolver ecuaciones radicales aislando el radical y elevando ambos lados de la ecuación a una potencia que coincida con el índice. Ver Ejemplo y Ejemplo.
- Para resolver ecuaciones de valor absoluto, necesitamos escribir dos ecuaciones, una para el valor positivo y otra para el valor negativo. Ver Ejemplo.
- Las ecuaciones en forma cuadrática son fáciles de detectar, ya que el exponente en el primer término es el doble del exponente en el segundo término y el tercer término es una constante. También podemos ver un binomio en lugar de la variable única. Utilizamos la sustitución para resolver. Ver Ejemplo y Ejemplo.
- Resolver una ecuación racional también puede conducir a una ecuación cuadrática o una ecuación en forma cuadrática. Ver Ejemplo.


