5.4: Gráficas de Funciones Polinómicas

Última actualización
Guardar como PDF

Page ID: 116934

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Objetivos de aprendizaje

Reconocer características de gráficas de funciones polinómicas.
Utilice la factorización para encontrar ceros de funciones polinómicas.
Identificar ceros y sus multiplicidades.
Determinar el comportamiento final.
Entender la relación entre grado y puntos de inflexión.
Graficar las funciones polinomiales.
Utilice el Teorema del Valor Intermedio.

Los ingresos en millones de dólares para una compañía de cable ficticia de 2006 a 2013 se muestran en la Tabla$\PageIndex{1}$.

Mesa$\PageIndex{1}$
Año	2006	2007	2008	2009	2010	2011	2012	2013
Ingresos	52.4	52.8	51.2	49.5	48.6	48.6	48.7	47.1

Los ingresos pueden ser modelados por la función polinómica

\[R(t)=−0.037t^4+1.414t^3−19.777t^2+118.696t−205.332\]

donde$R$ representa los ingresos en millones de dólares y$t$ representa el año, con$t=6$ correspondiente a 2006. ¿En qué intervalos van en aumento los ingresos para la empresa? ¿En qué intervalos disminuyen los ingresos para la empresa? Estas preguntas, junto con muchas otras, pueden ser respondidas examinando la gráfica de la función polinómica. Ya hemos explorado el comportamiento local de las cuadráticas, un caso especial de polinomios. En esta sección exploraremos el comportamiento local de los polinomios en general.

Reconocer las características de las gráficas de las funciones polinomiales

Las funciones polinómicas de grado 2 o más tienen gráficas que no tienen esquinas afiladas; recordemos que a este tipo de gráficas se les llama curvas suaves. Las funciones polinómicas también muestran gráficas que no tienen roturas. Las curvas sin roturas se denominan continuas. La figura$\PageIndex{1}$ muestra una gráfica que representa una función polinómica y una gráfica que representa una función que no es polinomio.

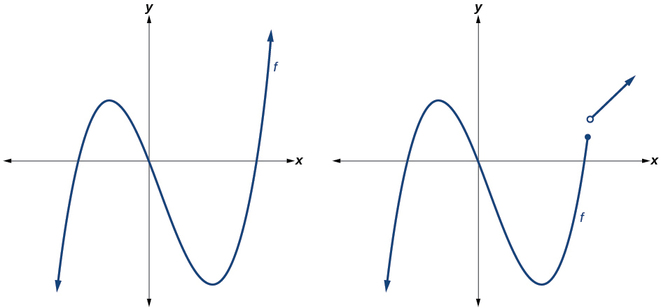
Gráfica de f (x) =x^3-0.01x — Figura$\PageIndex{1}$: Gráfica de$f(x)=x^3-0.01x$.

Ejemplo$\PageIndex{1}$: Recognizing Polynomial Functions

¿Cuál de las gráficas de la Figura$\PageIndex{2}$ representa una función polinómica?

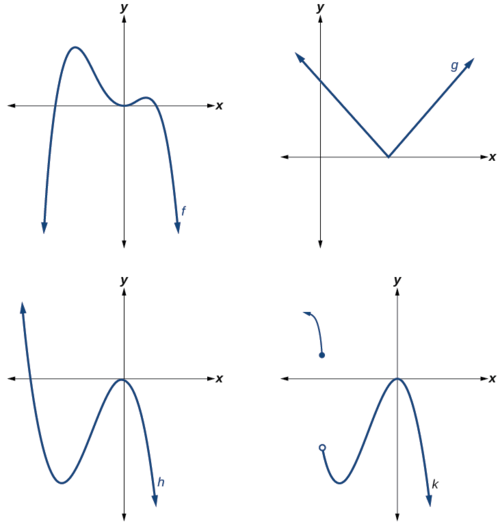
$Dos gráficas en las que una tiene una función polinómica y la otra tiene una función que se asemeja mucho a un polinomio pero no lo es. Dos gráficas en las que una tiene una función polinómica y la otra tiene una función que se asemeja mucho a un polinomio pero no lo es.$
Figura$\PageIndex{2}$

Solución

Las gráficas de$f$ y$h$ son gráficas de funciones polinómicas. Son lisos y continuos.
Las gráficas de$g$ y$k$ son gráficas de funciones que no son polinomios. La gráfica de función$g$ tiene una esquina afilada. La gráfica de la función no$k$ es continua.

Q&A

¿Todas las funciones polinómicas tienen como dominio todos los números reales?

Sí. Cualquier número real es una entrada válida para una función polinómica.

Uso de Factorización para Encontrar Ceros de Funciones Polinómicas

Recordemos que si$f$ es una función polinómica, cuyos valores$f(x)=0$ se denominan ceros de$f$.$x$ Si la ecuación de la función polinómica puede ser factorizada, podemos establecer cada factor igual a cero y resolver para los ceros.

Podemos usar este método para encontrar intercepciones x porque en las intercepciones x encontramos los valores de entrada cuando el valor de salida es cero. Para los polinomios generales, esta puede ser una perspectiva desafiante. Si bien las cuadráticas se pueden resolver usando la fórmula cuadrática relativamente simple, las fórmulas correspondientes para polinomios cúbicos y de cuarto grado no son lo suficientemente simples como para recordar, y las fórmulas no existen para polinomios generales de grado superior. En consecuencia, nos limitaremos a tres casos en este apartado:

El polinomio se puede factorizar utilizando métodos conocidos: mayor factor común y factorización trinomial.
El polinomio se da en forma factorizada.
La tecnología se utiliza para determinar las intercepciones.

HowTo: Dada una función polinómica$f$, find the x-intercepts by factoring

Set$f(x)=0$.
Si la función polinómica no se da en forma factorizada:
1. Destaca cualquier factor monomial común.
2. Factorizar cualquier binomio factoriable o trinomio.
Establezca cada factor igual a cero y resuelva para encontrar las intercepciones x.

Ejemplo$\PageIndex{2}$: Finding the x-Intercepts of a Polynomial Function by Factoring

Encuentra las intercepciones x de$f(x)=x^6−3x^4+2x^2$.

Solución

Podemos intentar factorizar este polinomio para encontrar soluciones para$f(x)=0$.

\[\begin{align*} x^6−3x^4+2x^2&=0 & &\text{Factor out the greatest common factor.} \\ x^2(x^4−3x^2+2)&=0 & &\text{Factor the trinomial.} \\ x^2(x^2−1)(x^2−2)&=0 & &\text{Set each factor equal to zero.} \end{align*}\]

\[\begin{align*} x^2&=0 & & & (x^2−1)&=0 & & & (x^2−2)&=0 \\ x^2&=0 & &\text{ or } & x^2&=1 & &\text{ or } & x^2&=2 \\ x&=0 &&& x&={\pm}1 &&& x&={\pm}\sqrt{2} \end{align*}\].

Esto nos da cinco intercepciones x:$(0,0)$$(1,0)$,$(−1,0)$,$(\sqrt{2},0)$, y$(−\sqrt{2},0)$ (Figura$\PageIndex{3}$). Podemos ver que esta es una función par.

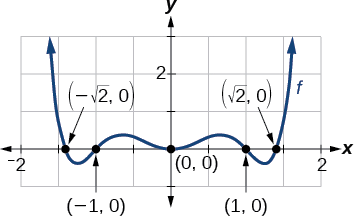
Una función uniforme — Figura$\PageIndex{3}$.

Ejemplo$\PageIndex{3}$: Finding the x-Intercepts of a Polynomial Function by Factoring

Encuentra las intercepciones x de$f(x)=x^3−5x^2−x+5$.

Solución

Encuentre soluciones para$f(x)=0$ factorización.

\[\begin{align*} x^3−5x^2−x+5&=0 &\text{Factor by grouping.} \\ x^2(x−5)−(x−5)&=0 &\text{Factor out the common factor.} \\ (x^2−1)(x−5)&=0 &\text{Factor the difference of squares.} \\ (x+1)(x−1)(x−5)&=0 &\text{Set each factor equal to zero.} \end{align*}\]

\[\begin{align*} x+1&=0 & &\text{or} & x−1&=0 & &\text{or} & x−5&=0 \\ x&=−1 &&& x&=1 &&& x&=5\end{align*}\]

Hay tres intercepciones x:$(−1,0)$,$(1,0)$, y$(5,0)$ (Figura$\PageIndex{4}$).

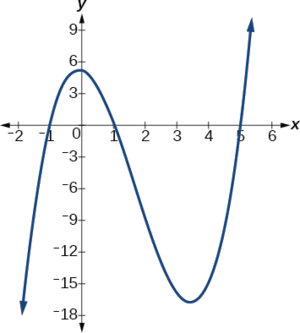
Gráfica de f (x) =x^3-5x^2-x+5 con sus tres intercepciones (-1, 0), (1, 0) y (5, 0). — Figura$\PageIndex{4}$: Gráfica de$f(x)$.

Ejemplo$\PageIndex{4}$: Finding the y- and x-Intercepts of a Polynomial in Factored Form

Encuentra las intercepciones y y x de$g(x)=(x−2)^2(2x+3)$.

Solución

La intercepción y se puede encontrar evaluando$g(0)$.

\[\begin{align*} g(0)&=(0−2)^2(2(0)+3) \\ &=12 \end{align*}\]

Entonces la intercepción y es$(0,12)$.

Las intercepciones x se pueden encontrar resolviendo$g(x)=0$.

\[(x−2)^2(2x+3)=0\]

\[\begin{align*} (x−2)^2&=0 & & & (2x+3)&=0 \\ x−2&=0 & &\text{or} & x&=−\dfrac{3}{2} \\ x&=2 \end{align*}\]

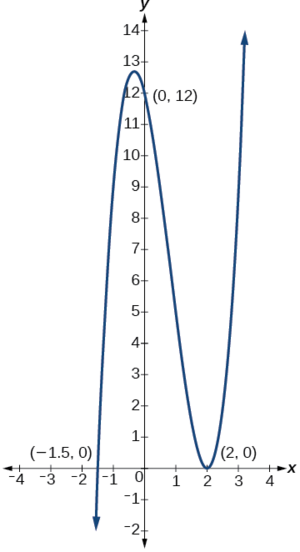
Entonces las intercepciones x son$(2,0)$ y$\left(−\dfrac{3}{2},0\right)$.

Análisis

Siempre podemos verificar que nuestras respuestas son razonables usando una calculadora gráfica para graficar el polinomio como se muestra en la Figura$\PageIndex{5}$.

Gráfica de g (x) = (x-2) ^2 (2x+3) con sus dos intercepciones x (2, 0) y (-3/2, 0) y su intersección y (0, 12). — Figura$\PageIndex{5}$: Gráfica de$g(x)$.

Ejemplo$\PageIndex{5}$: Finding the x-Intercepts of a Polynomial Function Using a Graph

Encuentra las intercepciones x de$h(x)=x^3+4x^2+x−6$.

Solución

Este polinomio no está en forma factorizada, no tiene factores comunes y no parece ser factorizable utilizando técnicas previamente discutidas. Afortunadamente, podemos usar la tecnología para encontrar las intercepciones. Ten en cuenta que algunos valores dificultan la gráfica a mano. En estos casos, podemos aprovechar las utilidades gráficas.

Al observar la gráfica de esta función, como se muestra en la Figura$\PageIndex{6}$, parece que hay intercepciones x en$x=−3,−2, \text{ and }1$.

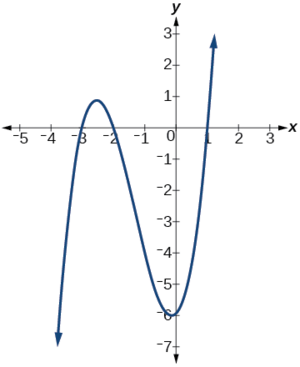
Gráfica de h (x) =x^3+4x^2+x-6. — Figura$\PageIndex{6}$: Gráfica de$h(x)$.

Podemos verificar si estos son correctos sustituyendo estos valores$x$ y verificando que
\[h(−3)=h(−2)=h(1)=0. \nonumber\]

Desde entonces$h(x)=x^3+4x^2+x−6$, tenemos:

\[ \begin{align*} h(−3)&=(−3)^3+4(−3)^2+(−3)−6=−27+36−3−6=0 \\[4pt] h(−2) &=(−2)^3+4(−2)^2+(−2)−6 =−8+16−2−6=0 \\[4pt] h(1)&=(1)^3+4(1)^2+(1)−6=1+4+1−6=0 \end{align*}\]

Cada intercepción x corresponde a un cero de la función polinómica y cada cero produce un factor, por lo que ahora podemos escribir el polinomio en forma factorizada.

\[\begin{align*} h(x)&=x^3+4x^2+x−6 \\ &=(x+3)(x+2)(x−1) \end{align*}\]

Ejercicio$\PageIndex{1}$

Encuentra las intercepciones y y x de la función$f(x)=x^4−19x^2+30x$.

Contestar

intercepción en y$(0,0)$;
intercepta x$(0,0)$,$(–5,0)$,$(2,0)$, y$(3,0)$

Identificación de ceros y sus multiplicidades

Las gráficas se comportan de manera diferente en varias intercepciones x. En ocasiones, la gráfica cruzará sobre el eje horizontal en una intersección. Otras veces, la gráfica tocará el eje horizontal y rebotará. Supongamos, por ejemplo, graficamos la función

\[f(x)=(x+3)(x−2)^2(x+1)^3.\]

Observe en Figura$\PageIndex{7}$ que el comportamiento de la función en cada una de las intercepciones x es diferente.

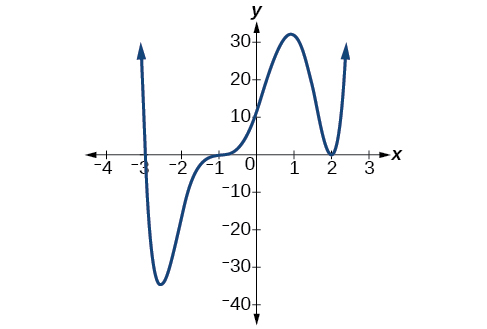
La intercepción x-3 es la solución de la ecuación$(x+3)=0$. El gráfico pasa directamente a través de la intercepción thex-en$x=−3$. El factor es lineal (tiene un grado de 1), por lo que el comportamiento cerca de la intersección es como el de una línea, pasa directamente a través de la intercepción. A esto lo llamamos un solo cero porque el cero corresponde a un solo factor de la función.

La intersección x 2 es la solución repetida de la ecuación$(x−2)^2=0$. La gráfica toca el eje en la intersección y cambia de dirección. El factor es cuadrático (grado 2), por lo que el comportamiento cerca de la intersección es como el de un cuadrático, rebota en el eje horizontal en la intersección.

\[(x−2)^2=(x−2)(x−2)\]

El factor se repite, es decir, el factor$(x−2)$ aparece dos veces. El número de veces que aparece un factor dado en la forma factorizada de la ecuación de un polinomio se llama multiplicidad. El cero asociado a este factor,$x=2$, tiene multiplicidad 2 porque el factor$(x−2)$ ocurre dos veces.

La intersección x −1 es la solución repetida del factor$(x+1)^3=0$. La gráfica pasa por el eje en la intersección, pero primero se aplana un poco. Este factor es cúbico (grado 3), por lo que el comportamiento cerca de la intersección es como el de un cubículo, con la misma forma de S cerca de la intersección que la función del kit de herramientas$f(x)=x^3$. A esto lo llamamos un triple cero, o un cero con multiplicidad 3.

Para ceros con multiplicidades pares, las gráficas tocan o son tangentes al eje x. Para ceros con multiplicidades impares, las gráficas cruzan o cruzan el eje x. Ver Figura$\PageIndex{8}$ para ejemplos de gráficas de funciones polinómicas con multiplicidad 1, 2 y 3.

Figura$\PageIndex{8}$: Tres gráficas que muestran tres funciones polinómicas diferentes con multiplicidad 1, 2 y 3.

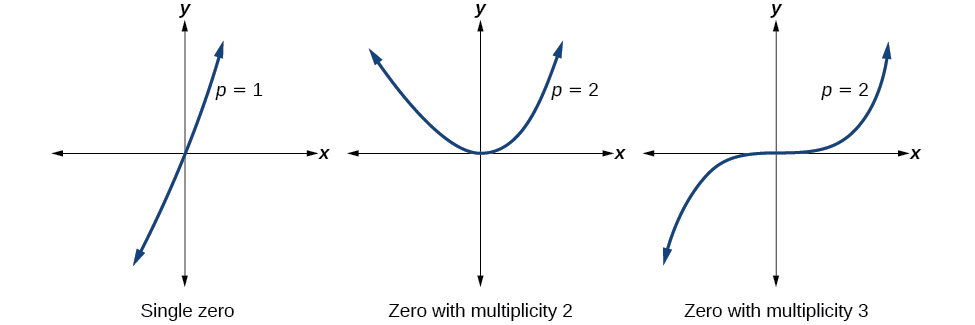
Para potencias pares superiores, como 4, 6 y 8, la gráfica seguirá tocándose y rebotando en el eje horizontal pero, por cada potencia par creciente, la gráfica aparecerá más plana a medida que se acerca y abandone el eje x.

Para potencias impares más altas, como 5, 7 y 9, la gráfica seguirá cruzando el eje horizontal, pero por cada potencia impar creciente, la gráfica aparecerá más plana a medida que se acerca y abandone el eje x.

Comportamiento Gráfico de Polinomios en Intercepciones X

Si un polinomio contiene un factor de la forma$(x−h)^p$, el comportamiento cerca de la intercepción x está determinado por la potencia$p$. Decimos que$x=h$ es un cero de multiplicidad$p$.

La gráfica de una función polinómica tocará el eje x en ceros con multiplicidades pares. La gráfica cruzará el eje x en ceros con multiplicidades impares.

La suma de las multiplicidades es el grado de la función polinómica.

CÓMO: Dada una gráfica de una función polinómica de grado$n$, identify the zeros and their multiplicities

Si la gráfica cruza el eje x y aparece casi lineal en la intersección, es un solo cero.
Si la gráfica toca el eje x y rebota fuera del eje, es un cero con multiplicidad par.
Si la gráfica cruza el eje x en un cero, es un cero con multiplicidad impar.
La suma de las multiplicidades es$n$.

Ejemplo$\PageIndex{6}$: Identifying Zeros and Their Multiplicities

Utilizar la gráfica de la función de grado 6 en la Figura$\PageIndex{9}$ para identificar los ceros de la función y sus posibles multiplicidades.

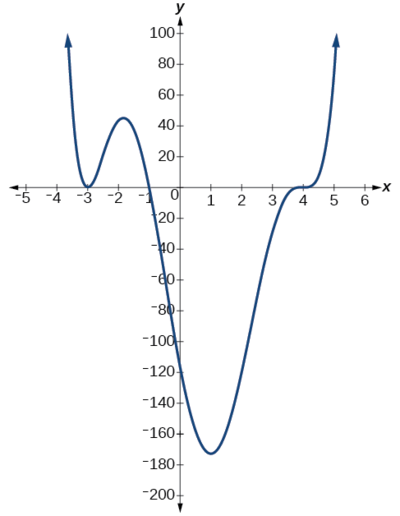
Gráfica de un polinomio de grado par con grado 6. — Figura$\PageIndex{9}$: Gráfica de una función polinómica con grado 5.

Solución

La función polinómica es de grado$n$. La suma de las multiplicidades debe ser$n$.

A partir de la izquierda, el primer cero ocurre en$x=−3$. La gráfica toca el eje x, por lo que la multiplicidad del cero debe ser pareja. El cero de −3 tiene multiplicidad 2.

El siguiente cero ocurre en$x=−1$. El gráfico se ve casi lineal en este punto. Este es un solo cero de multiplicidad 1.

El último cero ocurre en$x=4$ .La gráfica cruza el eje x, por lo que la multiplicidad del cero debe ser impar. Sabemos que la multiplicidad es probable 3 y que la suma de las multiplicidades es probable 6.

Ejercicio$\PageIndex{2}$

Utilice la gráfica de la función de grado 5 en la Figura$\PageIndex{10}$ para identificar los ceros de la función y sus multiplicidades.

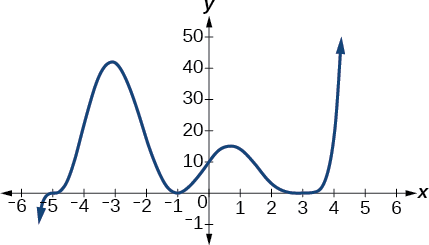
$Gráfica de una función polinómica con grado 5.$

Figura$\PageIndex{10}$: Gráfica de una función polinómica con grado 5.

Contestar: La gráfica tiene un cero de —5 con multiplicidad 1, un cero de —1 con multiplicidad 2 y un cero de 3 con multiplicidad par.

Determinar el comportamiento final

Como ya hemos aprendido, el comportamiento de una gráfica de una función polinómica de la forma

\[f(x)=a_nx^n+a_{n−1}x^{n−1}+...+a_1x+a_0\]

o bien en última instancia subirá o bajará a medida que$x$ aumenta sin límite y bien subirá o bajará como$x$ disminuciones sin límite. Esto se debe a que para entradas muy grandes, digamos 100 o 1,000, el término principal domina el tamaño de la salida. Lo mismo es cierto para entradas muy pequeñas, digamos —100 o —1,000.

Recordemos que llamamos a este comportamiento el comportamiento final de una función. Como señalamos al discutir ecuaciones cuadráticas, cuando el término principal de una función polinómica,$a_nx^n$, es una función de potencia par, ya que$x$ aumenta o disminuye sin límite,$f(x)$ aumenta sin límite. Cuando el término principal es una función de potencia impar, como$x$ disminuye sin límite,$f(x)$ también disminuye sin límite; a medida que$x$ aumenta sin límite,$f(x)$ también aumenta sin límite. Si el término principal es negativo, cambiará la dirección del comportamiento final. La figura$\PageIndex{11}$ resume los cuatro casos.

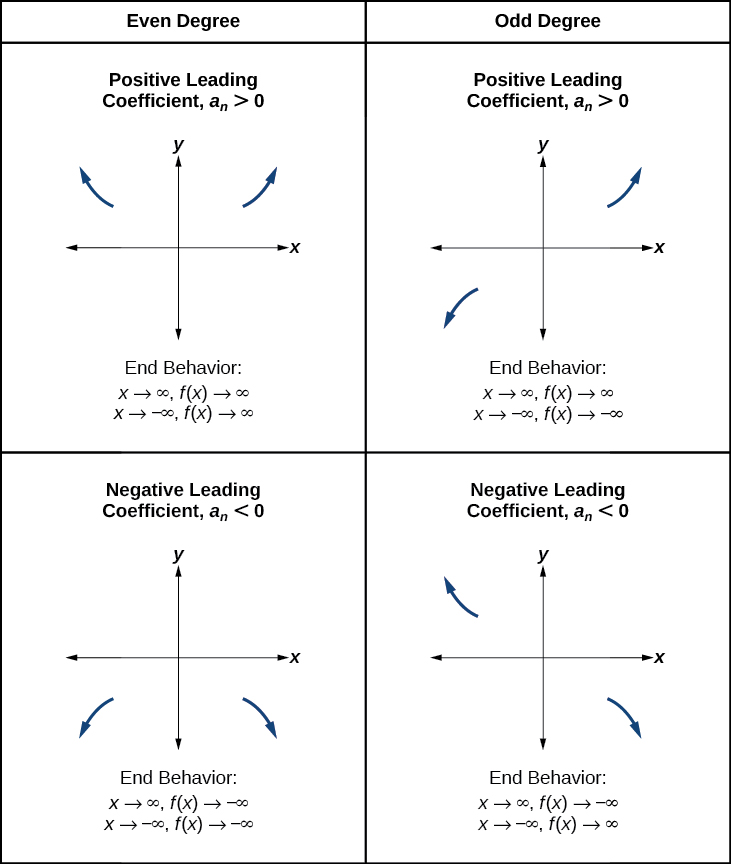
Tabla que muestra el comportamiento final de polinomios pares e impares con coeficientes positivos y negativos — Figura$\PageIndex{11}$.

Comprender la relación entre grado y puntos de inflexión

Además del comportamiento final, recordemos que podemos analizar el comportamiento local de una función polinómica. Puede tener un punto de inflexión donde la gráfica cambia de aumentar a disminuir (de subir a caer) o de disminuir a aumentar (de caer a subir). Observa la gráfica de la función polinómica$f(x)=x^4−x^3−4x^2+4x$ en la Figura$\PageIndex{12}$. La gráfica tiene tres puntos de inflexión.

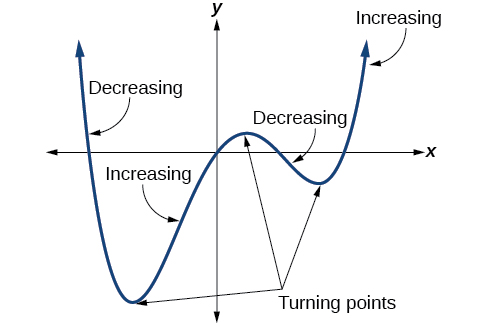
Gráfico de f (x) =x^4-x^3-4x^2+4x que denota donde la función aumenta y disminuye y sus puntos de inflexión. — Figura$\PageIndex{12}$: Gráfica de$f(x)=x^4-x^3-4x^2+4x$

Esta función$f$ es una función polinómica de 4to grado y tiene 3 puntos de inflexión. El número máximo de puntos de inflexión de una función polinómica es siempre uno menor que el grado de la función.

Definición: Interpretación de los puntos de inflexión

Un punto de inflexión es un punto de la gráfica donde el gráfico cambia de aumentar a disminuir (de subir a caer) o de disminuir a aumentar (de caer a subir). Un polinomio de grado$n$ tendrá como máximo puntos de$n−1$ inflexión.

Ejemplo$\PageIndex{7}$: Finding the Maximum Number of Turning Points Using the Degree of a Polynomial Function

Encuentra el número máximo de puntos de inflexión de cada función polinómica.

$f(x)=−x^3+4x^5−3x^2+1$
$f(x)=−(x−1)^2(1+2x^2)$

Solución

a.$f(x)=−x^3+4x^5−3x^2+1$

Primero, reescribe la función polinómica en orden descendente:$f(x)=4x^5−x^3−3x^2+1$

Identificar el grado de la función polinómica. Esta función polinómica es de grado 5.

El número máximo de puntos de inflexión es$5−1=4$.

b.$f(x)=−(x−1)^2(1+2x^2)$

Primero, identificar el término principal de la función polinómica si la función se expandió.

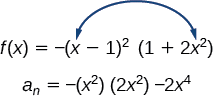
$imageedit_33_3540887475.png$

Luego, identificar el grado de la función polinómica. Esta función polinómica es de grado 4.

El número máximo de puntos de inflexión es$4−1=3$.

Graficar funciones polinomiales

Podemos usar lo que hemos aprendido sobre multiplicidades, comportamiento final y puntos de inflexión para dibujar gráficos de funciones polinómicas. Pongamos todo esto junto y veamos los pasos requeridos para graficar las funciones polinomiales.

Cómo: Dada una función polinómica, bosquejar la gráfica

Encuentra las intercepciones.
Compruebe si hay simetría. Si la función es una función par, su gráfica es simétrica alrededor del eje y, es decir,$f(−x)=f(x)$. Si una función es una función impar, su gráfica es simétrica sobre el origen, es decir,$f(−x)=−f(x)$.
Utilice las multiplicidades de los ceros para determinar el comportamiento del polinomio en las intercepciones x.
Determinar el comportamiento final examinando el término principal.
Utilice el comportamiento final y el comportamiento en las intercepciones para bosquejar una gráfica.
Asegurar que el número de puntos de inflexión no exceda uno menos que el grado del polinomio.
Opcionalmente, use tecnología para verificar la gráfica.

Ejemplo$\PageIndex{8}$: Sketching the Graph of a Polynomial Function

Esbozar una gráfica de$f(x)=−2(x+3)^2(x−5)$.

Solución

Esta gráfica tiene dos intercepciones x. At$x=−3$, el factor es cuadrado, lo que indica una multiplicidad de 2. El gráfico rebotará en esta intercepción x. At$x=5$, la función tiene una multiplicidad de uno, lo que indica que la gráfica cruzará a través del eje en esta intersección.

La intercepción y se encuentra evaluando$f(0)$.

\[\begin{align*} f(0)&=−2(0+3)^2(0−5) \\ &=−2⋅9⋅(−5) \\ &=90 \end{align*}\]

La intercepción y es$(0,90)$.

Adicionalmente, podemos ver el término principal, si este polinomio se multiplicara, sería$−2x3$, por lo que el comportamiento final es el de un cúbico reflejado verticalmente, con las salidas disminuyendo a medida que las entradas se acercan al infinito, y las salidas aumentando a medida que las entradas se acercan al infinito negativo. Ver Figura$\PageIndex{13}$.

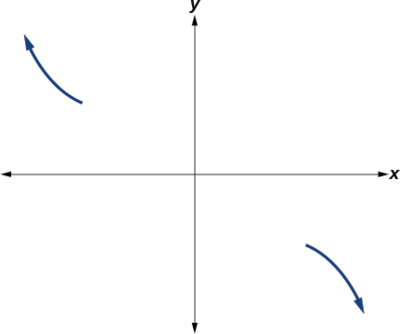
Mostrando la distribución para el término principal. — Figura$\PageIndex{13}$: Muestra la distribución para el término principal.

Para bosquejar esto, consideramos que:

Como$x{\rightarrow}−{\infty}$ la función$f(x){\rightarrow}{\infty}$, así sabemos que la gráfica comienza en el segundo cuadrante y está disminuyendo hacia el eje x.
Dado que no$f(−x)=−2(−x+3)^2(−x–5)$ es igual a$f(x)$, la gráfica no muestra simetría.
At$(−3,0)$, la gráfica rebota en el eje transversal, por lo que la función debe comenzar a aumentar.
At$(0,90)$, la gráfica cruza el eje y en la intercepción y. Ver Figura$\PageIndex{14}$.

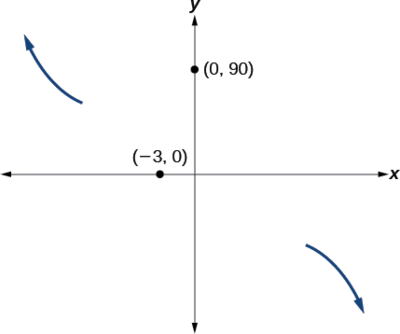
Gráfica del comportamiento final e intercepciones, (-3, 0) y (0, 90), para la función f (x) =-2 (x+3) ^2 (x-5). — Figura$\PageIndex{14}$: Gráfica del comportamiento final e intercepciones,$(-3, 0)$ y$(0, 90)$, para la función$f(x)=-2(x+3)^2(x-5)$.

En algún lugar después de este punto, la gráfica debe volver a bajar o comenzar a disminuir hacia el eje horizontal porque la gráfica pasa por la siguiente intercepción en$(5,0)$. Ver Figura$\PageIndex{15}$.

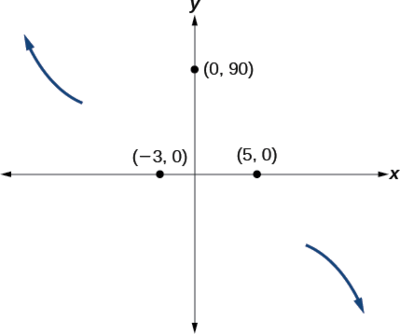
Gráfica del comportamiento final e intercepciones, (-3, 0), (0, 90) y (5, 0), para la función f (x) =-2 (x+3) ^2 (x-5). — Figura$\PageIndex{15}$: Gráfica del comportamiento final e intercepciones$(-3, 0)$,$(0, 90)$ y$(5, 0)$, para la función$f(x)=-2(x+3)^2(x-5)$.

Como$x{\rightarrow}{\infty}$ la función$f(x){\rightarrow}−{\infty}$,

así sabemos que la gráfica sigue disminuyendo, y podemos dejar de dibujar la gráfica en el cuarto cuadrante.

Utilizando la tecnología, podemos crear la gráfica para la función polinómica, que se muestra en la Figura$\PageIndex{16}$, y verificar que la gráfica resultante se parece a nuestro boceto en la Figura$\PageIndex{15}$.

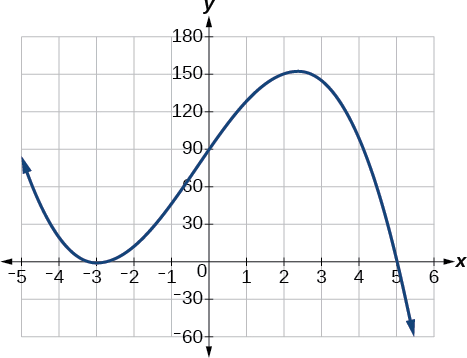
$El gráfico completo de la función polinómica f (x) =−2 (x+3) ^2 (x−5)$
Figura$\PageIndex{16}$: La gráfica completa de la función polinómica$f(x)=−2(x+3)^2(x−5)$.

Ejercicio$\PageIndex{8}$

Esbozar una gráfica de$f(x)=\dfrac{1}{4}x(x−1)^4(x+3)^3$.

Contestar: $alt$
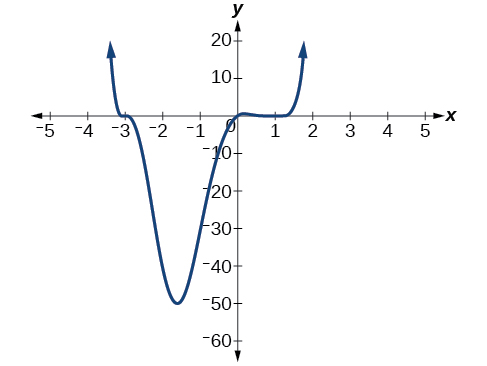
Figura$\PageIndex{17}$: Gráfica de$f(x)=\frac{1}{4}x(x−1)^4(x+3)^3$

Uso del Teorema del Valor Intermedio

En algunas situaciones, podemos conocer dos puntos en una gráfica pero no los ceros. Si esos dos puntos están en lados opuestos del eje x, podemos confirmar que hay un cero entre ellos. Considera una función polinómica$f$ cuya gráfica es suave y continua. El Teorema del Valor Intermedio establece que para dos números$a$ y$b$ en el dominio de$f$$f(a){\neq}f(b)$, si$a<b$ y, entonces la función$f$ adquiere cada valor entre$f(a)$ y$f(b)$. Podemos aplicar este teorema a un caso especial que sea útil para graficar funciones polinomiales. Si un punto en la gráfica de una función$f$ continua$x=a$ se encuentra por encima del eje x y otro punto en$x=b$ se encuentra por debajo del eje thex-axis, debe existir un tercer punto entre$x=a$ y$x=b$ donde la gráfica cruza el eje x. Llama a este$(c,f(c))$ punto.Esto significa que tenemos la seguridad de que hay una solución$c$ donde$f(c)=0$.

En otras palabras, el Teorema del Valor Intermedio nos dice que cuando una función polinómica cambia de un valor negativo a un valor positivo, la función debe cruzar el eje x. La figura$\PageIndex{18}$ muestra que hay un cero entre$a$ y$b$.

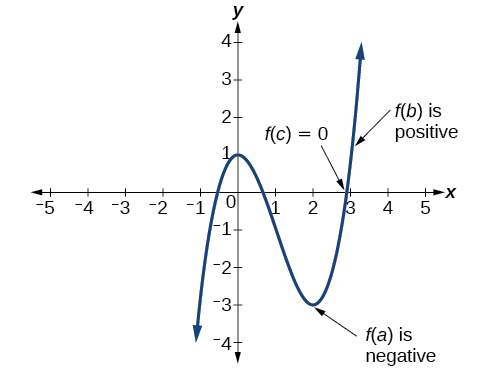
Gráfico de una función polinómica de grado impar que muestra un punto f (a) que es negativo, f (b) que es positivo y f (c) que es 0. — Figura$\PageIndex{18}$: Usando el Teorema del Valor Intermedio para mostrar que existe un cero.

Definición: Teorema del Valor Intermedio

Dejar$f$ ser una función polinómica. El Teorema del Valor Intermedio establece que si$f(a)$ y$f(b)$ tienen signos opuestos, entonces existe al menos un valor$c$ entre$a$ y$b$ para el cual$f(c)=0$.

Ejemplo$\PageIndex{9}$: Using the Intermediate Value Theorem

Demostrar que la función$f(x)=x^3−5x^2+3x+6$ tiene al menos dos ceros reales entre$x=1$ y$x=4$.

Solución

Como inicio, evaluar$f(x)$ en los valores enteros$x=1,\;2,\;3,\; \text{and }4$ (Tabla$\PageIndex{2}$).

Mesa$\PageIndex{2}$
$x$	1	2	3	4
$f(x)$	5	0	-3	2

Vemos que un cero ocurre en$x=2$. También, dado que$f(3)$ es negativo y$f(4)$ es positivo, por el Teorema del Valor Intermedio, debe haber al menos un cero real entre 3 y 4.

Hemos demostrado que hay al menos dos ceros reales entre$x=1$ y$x=4$.

Análisis

También podemos ver en la gráfica de la función en Figura$\PageIndex{19}$ que hay dos ceros reales entre$x=1$ y$x=4$.

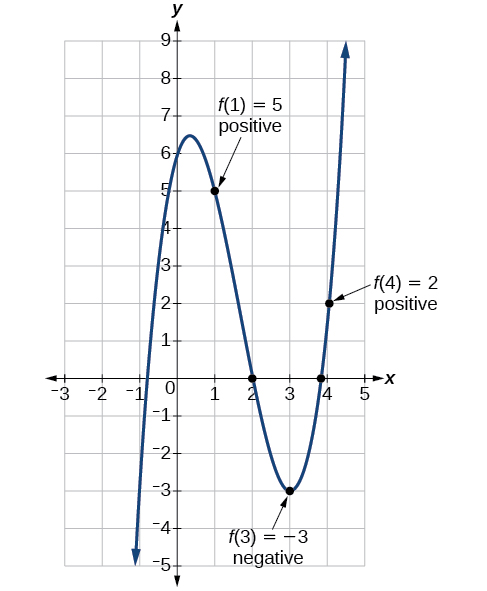
Gráfica de f (x) =x^3-5x^2+3x+6 y muestra, por el Teorema del Valor Intermedio, que existen dos ceros ya que f (1) =5 y f (4) =2 son positivos y f (3) = -3 es negativo. — Figura$\PageIndex{19}$.

Ejercicio$\PageIndex{4}$

Demostrar que la función$f(x)=7x^5−9x^4−x^2$ tiene al menos un cero real entre$x=1$ y$x=2$.

Contestar: Porque$f$ es una función polinómica y dado que$f(1)$ es negativa y$f(2)$ es positiva, hay al menos un cero real entre$x=1$ y$x=2$.

Escribir fórmulas para funciones polinomiales

Ahora que sabemos encontrar ceros de funciones polinómicas, podemos utilizarlos para escribir fórmulas basadas en gráficas. Debido a que una función polinómica escrita en forma factorizada tendrá una intercepción x donde cada factor es igual a cero, podemos formar una función que pasará a través de un conjunto de intercepciones x introduciendo un conjunto de factores correspondientes.

Nota: Forma factorizada de polinomios

Si un polinomio de grado más bajo$p$ tiene intercepciones horizontales en$x=x_1,x_2,…,x_n$, entonces el polinomio se puede escribir en la forma factorizada:$f(x)=a(x−x_1)^{p_1}(x−x_2)^{p_2}⋯(x−x_n)^{p_n}$ donde las potencias$p_i$ en cada factor pueden ser determinadas por el comportamiento de la gráfica en la intercepción correspondiente, y el factor de estiramiento$a$ se puede determinar dado un valor de la función que no sea la intercepción x.

$alt$ Dada una gráfica de una función polinómica, escriba una fórmula para la función.

Identificar las intercepciones x de la gráfica para encontrar los factores del polinomio.
Examinar el comportamiento de la gráfica en las intercepciones x para determinar la multiplicidad de cada factor.
Encuentra el polinomio de menor grado que contiene todos los factores encontrados en el paso anterior.
Use cualquier otro punto en la gráfica (la intersección y puede ser la más fácil) para determinar el factor de estiramiento.

Ejemplo$\PageIndex{10}$: Writing a Formula for a Polynomial Function from the Graph

Escribe una fórmula para la función polinómica que se muestra en la Figura$\PageIndex{20}$.

Gráfica de un polinomio positivo de grado par con ceros a x=-3, 2, 5 e y=-2. — Figura$\PageIndex{20}$.

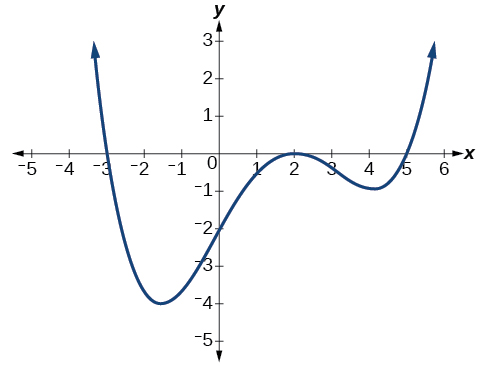
Solución

Esta gráfica tiene tres intercepciones x:$x=−3,\;2,\text{ and }5$. La intersección y se ubica en$(0,2)$ At$x=−3$ y$ x=5$, la gráfica pasa por el eje linealmente, sugiriendo que los factores correspondientes del polinomio serán lineales. At$x=2$, la gráfica rebota en la intersección, sugiriendo que el factor correspondiente del polinomio será segundo grado (cuadrático). Juntos, esto nos da

\[f(x)=a(x+3)(x−2)^2(x−5)\]

Para determinar el factor de estiramiento, utilizamos otro punto en la gráfica. Vamos a utilizar la intercepción y$(0,–2)$, para resolver para$a$.

\[\begin{align*} f(0)&=a(0+3)(0−2)^2(0−5) \\ −2&=a(0+3)(0−2)^2(0−5) \\ −2&=−60a \\ a&=\dfrac{1}{30} \end{align*}\]

El polinomio graficado parece representar la función$f(x)=\dfrac{1}{30}(x+3)(x−2)^2(x−5)$.

Ejercicio$\PageIndex{5}$

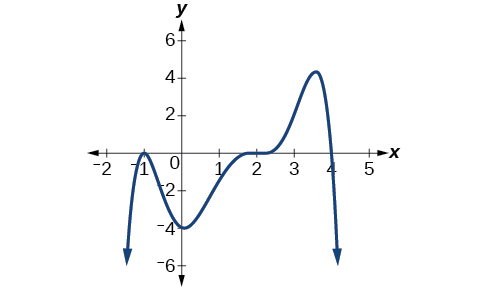
Dada la gráfica que se muestra en la Figura$\PageIndex{21}$, escriba una fórmula para la función mostrada.

Gráfica de un polinomio negativo de grado par con ceros a x=-1, 2, 4 e y=-4. — Figura$\PageIndex{21}$.

Contestar: $f(x)=−\frac{1}{8}(x−2)^3(x+1)^2(x−4)$

Uso de Extremas Locales y Globales

Con cuadráticas, pudimos encontrar algebraicamente el valor máximo o mínimo de la función al encontrar el vértice. Para polinomios generales, encontrar estos puntos de inflexión no es posible sin técnicas más avanzadas del cálculo. Incluso entonces, encontrar dónde ocurren los extremos aún puede ser un desafío algebraico. Por ahora, estimaremos las ubicaciones de los puntos de inflexión utilizando la tecnología para generar una gráfica.

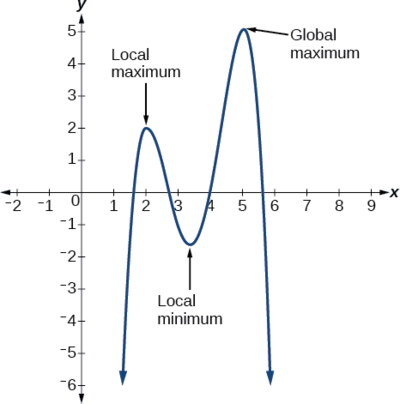
Cada punto de inflexión representa un mínimo o máximo local. En ocasiones, un punto de inflexión es el punto más alto o más bajo de toda la gráfica. En estos casos, decimos que el punto de inflexión es un máximo global o un mínimo global. Estos también se conocen como los valores máximos absolutos y mínimos absolutos de la función.

Nota: Extrema Local y Global

Un máximo local o mínimo local at$x=a$ (a veces llamado el máximo o mínimo relativo, respectivamente) es la salida en el punto más alto o más bajo de la gráfica en un intervalo abierto$x=a$ alrededor.Si una función tiene un máximo local en$a$, entonces$f(a){\geq}f(x)$ para todos $x$en un intervalo abierto alrededor$x=a$. Si una función tiene un mínimo local en$a$, entonces$f(a){\leq}f(x)$ para todos$x$ en un intervalo abierto alrededor$x=a$.

Un máximo global o mínimo global es la salida en el punto más alto o más bajo de la función. Si una función tiene un máximo global en$a$, entonces$f(a){\geq}f(x)$ para todos$x$. Si una función tiene un mínimo global en$a$, entonces$f(a){\leq}f(x)$ para todos$x$.

Podemos ver la diferencia entre los extremos locales y globales en la Figura$\PageIndex{22}$.

Figura$\PageIndex{22}$: Gráfica de un polinomio de grado par que denota el máximo y mínimo local y el máximo global.

$alt$ ¿Todas las funciones polinómicas tienen un mínimo o máximo global?

No. Sólo las funciones polinómicas de grado par tienen un mínimo o máximo global. Por ejemplo, no$f(x)=x$ tiene un máximo global ni un mínimo global.

Ejemplo$\PageIndex{11}$: Using Local Extrema to Solve Applications

Se construirá una caja abierta cortando cuadrados de cada esquina de una lámina de plástico de 14 cm por 20 cm y luego doblando los lados. Encuentra el tamaño de los cuadrados que deben recortarse para maximizar el volumen encerrado por la caja.

Solución

Comenzaremos este problema dibujando una imagen como la de la Figura$\PageIndex{23}$, etiquetando el ancho de los cuadrados recortados con una variable,$w$.

Figura$\PageIndex{23}$: Diagrama de un rectángulo con cuatro cuadrados en las esquinas.

Observe que después de cortar un cuadrado de cada extremo, deja$a(14−2w)$ cm por$(20−2w)$ cm rectángulo para la base de la caja, y la caja tendrá$w$ cm de altura. Esto le da el volumen

\[\begin{align*} V(w)&=(20−2w)(14−2w)w \\ &=280w−68w^2+4w^3 \end{align*}\]

Observe, ya que los factores son$20–2w$$14–2w$,$w$, y, los tres ceros son$10, \,7,$ y$0,) respectively. Because a height of \(0$ cm no es razonable, consideramos que los únicos ceros$10$ y$7.$ El lado más corto es$14$ y estamos cortando dos cuadrados, por lo que los valores$w$ pueden tomar son mayor que cero o menor que$7.$ Esto significa que restringiremos el dominio de esta función a$0<w<7$ .Usando tecnología para bosquejar la gráfica de$V(w)$ en este dominio razonable, obtenemos una gráfica como esa en la Figura$\PageIndex{24}$. Podemos usar esta gráfica para estimar el valor máximo para el volumen, restringido a valores para$w$ que sean razonables para este problema, valores de 0 a 7.

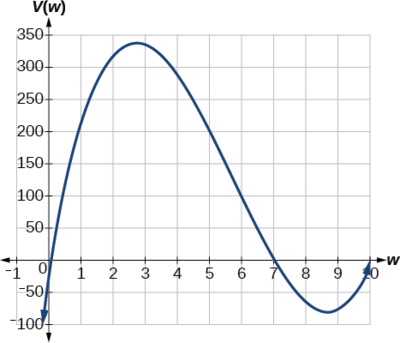
Gráfica de V (w) = (20-2w) (14-2w) w donde el eje x se etiqueta w y el eje y se etiqueta V (w). — Figura$\PageIndex{24}$: Gráfica de$V(w)=(20-2w)(14-2w)w$

A partir de esta gráfica, volvemos nuestro enfoque solo a la porción en el dominio razonable,$[0, 7]$. Podemos estimar que el valor máximo es de alrededor de 340 cm cúbicos, lo que ocurre cuando los cuadrados son de aproximadamente 2.75 cm en cada lado. Para mejorar esta estimación, podríamos usar funciones avanzadas de nuestra tecnología, si están disponibles, o simplemente cambiar nuestra ventana para acercar nuestra gráfica y producir Figura$\PageIndex{25}$.

Gráfica de V (w) = (20-2w) (14-2w) w donde el eje x se etiqueta w y el eje y se etiqueta V (w) en el dominio [2.4, 3]. — Figura$\PageIndex{25}$: Gráfica de$V(w)=(20-2w)(14-2w)w$.

A partir de esta vista ampliada, podemos refinar nuestra estimación para el volumen máximo a aproximadamente 339 cm cúbicos, cuando los cuadrados miden aproximadamente 2.7 cm en cada lado.

Ejercicio$\PageIndex{1}$

Utilice la tecnología para encontrar los valores máximo y mínimo en el intervalo$[−1,4]$ de la función$f(x)=−0.2(x−2)^3(x+1)^2(x−4)$.

Contestar: El mínimo ocurre aproximadamente en el punto$(0,−6.5)$,
y el máximo ocurre aproximadamente en el punto$(3.5,7)$.

Conceptos clave

Las funciones polinómicas de grado 2 o más son funciones suaves y continuas.
Para encontrar los ceros de una función polinómica, si se puede factorizar, factorizar la función y establecer cada factor igual a cero.
Otra forma de encontrar las intercepciones x de una función polinómica es graficar la función e identificar los puntos en los que la gráfica cruza el eje x.
La multiplicidad de un cero determina cómo se comporta la gráfica en las intercepciones x.
La gráfica de un polinomio cruzará el eje horizontal en un cero con multiplicidad impar.
La gráfica de un polinomio tocará el eje horizontal en un cero con multiplicidad uniforme.
El comportamiento final de una función polinómica depende del término principal.
La gráfica de una función polinómica cambia de dirección en sus puntos de inflexión.
Una función polinómica de grado$n$ tiene como máximo puntos de$n−1$ inflexión.
Para graficar las funciones polinomiales, encontrar los ceros y sus multiplicidades, determinar el comportamiento final y asegurar que la gráfica final tenga como máximo puntos de$n−1$ inflexión.
Graficar una función polinómica ayuda a estimar los extremos locales y globales.
El Teorema del Valor Intermedio nos dice que si$f(a)$ y$f(b)$ tienen signos opuestos, entonces existe al menos un valor$c$ entre$a$ y$b$ para el cual$f(c)=0$.

Glosario

máximo global punto de inflexión
más alto en una gráfica;$f(a)$ donde$f(a){\geq}f(x)$ para todos$x$.

mínimo global punto de inflexión
más bajo en una gráfica;$f(a)$ donde$f(a){\leq}f(x)$ para todos$x$.

Teorema de Valor Intermedio
para dos números$a$ y$b$ en el dominio de$f$$f(a){\neq}f(b)$, if$a<b$ y, entonces la funciónf adquiere cada valor entre$f(a)$ y$f(b)$; específicamente, cuando una función polinómica cambia de un valor negativo a un valor positivo, la función debe cruzar el eje x

multiplicidad
el número de veces que un factor dado aparece en la forma factorizada de la ecuación de un polinomio; si un polinomio contiene un factor de la forma$(x−h)^p$,$x=h$ es un cero de multiplicidad$p$.

Search

Text Color

Text Size

Margin Size

Font Type

Mesa\(\PageIndex{2}\)
\(x\)	1	2	3	4
\(f(x)\)	5	0	-3	2