1.6: El grupo unimodular SL (n, R) y la invarianza de volumen

Última actualización
Guardar como PDF

Page ID: 110014

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Es bien sabido que el volumen de un paralelepípedo abarcado por vectores linealmente independientes viene dado por el determinante de los componentes del vector. Por lo tanto, es evidente que una transformación con una matriz unimodular deja esta expresión para el volumen invariante.

Sin embargo, la situación tiene algunos aspectos sutiles que exigen un examen más detallado. Si bien el cálculo de volumen y área se encuentra entre los procedimientos estándar de geometría, esto generalmente se lleva a cabo en espacios métricos, en los que la longitud y el ángulo tienen su conocido significado euclidiano. Sin embargo, esta es una suposición demasiado restrictiva, y la fórmula determinantal puede justificarse también dentro de la geometría afín sin usar conceptos métricos.

Dado que en repetidas ocasiones nos encontraremos con tales situaciones, explicamos brevemente la idea subyacente para el caso de áreas en un espacio vectorial bidimensional$\mathcal{V}(2, R)$.

Avanzamos dos postulados:

El área es una cantidad aditiva: el área de una figura es igual a la suma de las áreas de sus partes.
Las cifras traslacionalmente congruentes tienen áreas iguales.

(El punto es que la congruencia euclidiana 'implica también congruencia rotacional, que no está disponible para nosotros debido a la ausencia de métrica).

Procedemos ahora en pasos sucesivos como se muestra en la Figura 1.2.

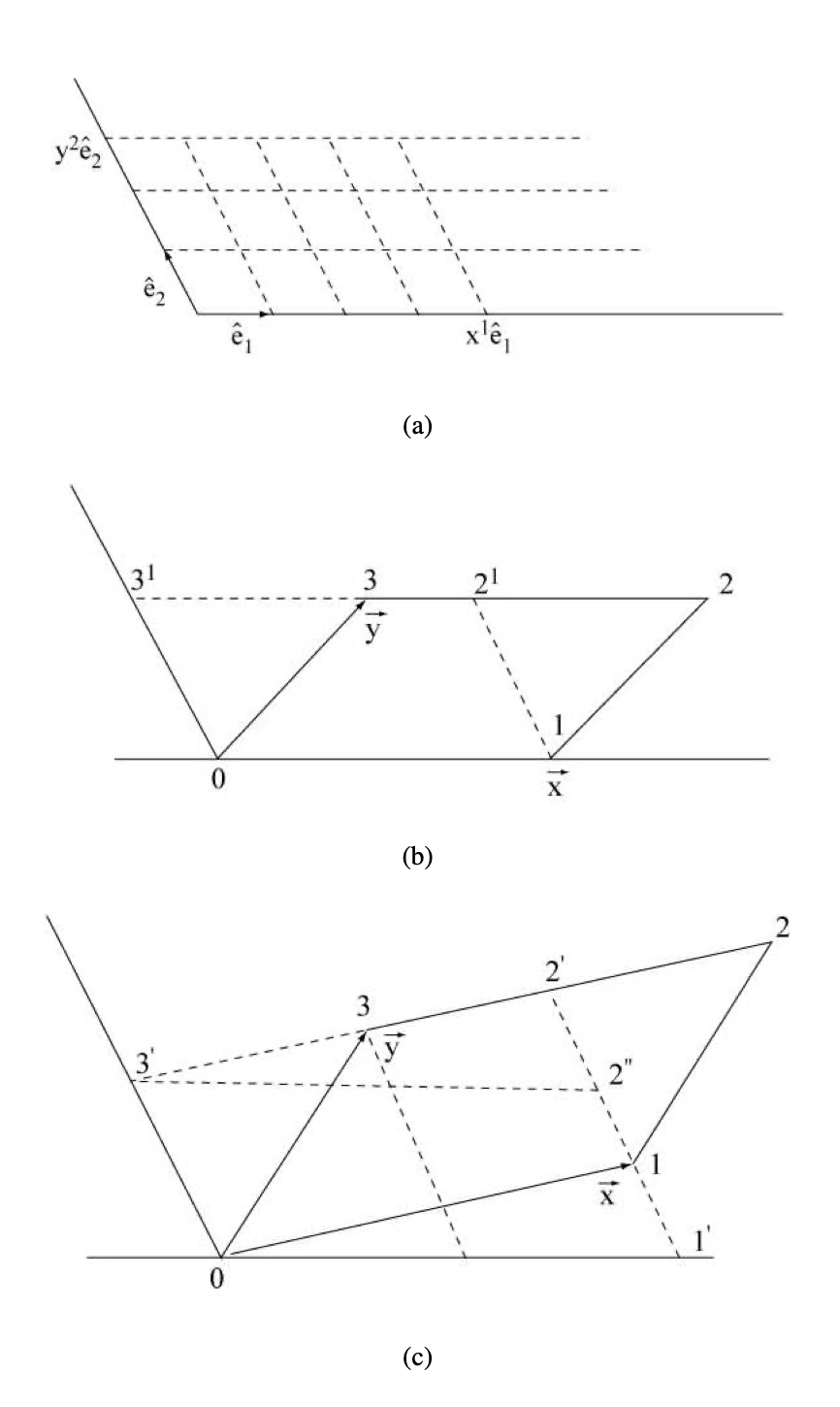
$Screen Shot 2020-07-06 at 3.19.11 PM.png$

Figura 1.2: Congruencia traslacional y área igual.

Considerar al principio los vectores

$\vec{x} = x^{1} \vec{e}_{1}$

$\vec{y} = y^{2} \vec{e}_{2}$

donde las coordenadas son números enteros (Figura 1.2a). El área relativa a la celda unitaria se obtiene a través del simple conteo como$x^{1}y^{2}$. El mismo resultado puede justificarse para cualquier valor real para las coordenadas por subdivisión y un proceso limitante.

Se nos permite escribir este resultado en forma determinantal:

\[\begin{array}{c} {x^{1}y^{2} = \begin{vmatrix} {x^1}&{0}\\ {0}&{y^2} \end{vmatrix}} \end{array}\]

Si los vectores

\[\vec{x} = x^{1} \vec{e}_{1}+x^{2} \vec{e}_{2}\]

\[\vec{y} = y^{1} \vec{e}_{1}+y^{2} \vec{e}_{2}\]

no coinciden con los ejes de coordenadas, la coincidencia se puede lograr en no más de dos pasos (Figuras 1.2b y 1.2c) utilizando la congruencia traslacional de los paralelogramos$(0123) (012’3’) (012”3’)$.

Por un argumento geométrico elemental se concluye a partir de aquí que el área abarcada por$\vec{x}$ y$\vec{y}$ es igual al área abarcada por$\hat{e}_{1}$ y$\hat{e}_{2}$ multiplicada por el determinante

\[\begin{array}{c} {\begin{vmatrix} {x^1}&{x^2}\\ {y^1}&{y^2} \end{vmatrix}} \end{array}\]

Este resultado puede justificarse también de una manera más elegante: Las operaciones geométricas en las figuras b y c consisten en sumar el múltiplo del vector$\vec{y}$ al vector$\vec{x}$, o agregar el múltiplo de la segunda fila del determinante a la primera fila, y sabemos que tales operaciones dejan el valor del determinante sin cambios.

La conexión entre determinante y área puede generalizarse a tres y más dimensiones, aunque el argumento geométrico directo se volvería cada vez más engorroso.

Este defecto será remediado de manera más efectiva en términos del álgebra de Grassmann que se desarrollará en el Capítulo VII.