3.1: Grupos Electrógenos
( \newcommand{\kernel}{\mathrm{null}\,}\)
Ahora hemos visto algunos tipos diferentes de grupos: grupos de simetrías de un objeto geométrico, enteros bajo suma, enteros módulon, and permutations. We can easily visualize the objects related to the group - like the geometric object, numbers, or the braid notation for permutations - but how can we visualize the group itself?
Una excelente manera de hacerlo es identificar un conjunto de generadores para el grupo. En un grupo siempre podemos combinar algunos elementos usando la operación de grupo para obtener otro elemento de grupo. Los generadores son algunos elementos especiales que seleccionamos los cuales se pueden utilizar para llegar a cualquier otro elemento del grupo.
Como ejemplo, recordemos el grupo diedro, las simetrías de unn-sided polygon. There are 2n symmetries in all, but we can build up any of the symmetries using just a small rotation and a flip. For the symmetries of the equilateral triangle, we let ρ denote the rotation by 120 degrees, and let f be the flip over one of the axes of the triangle. Then the six elements of the dihedral group are given by: id,ρ,ρ2,f,fρ,fρ2. Thus, {f,ρ} is a set of generators for the dihedral group.
Aquí está la definición formal:
VamosG be a group, and S a subset of G. We say that S generates G (and that S is a set of generators for G) if every element of G can be expressed as a product of elements of S and their inverses.
Incluimos las inversas de los generadores en la definición porque sabemos que cada elemento tiene una inversa. Si pensamos en los enteros en suma, podemos escribir cada número positivo como una suma de muchas veces del número1: for example, 5 is just 1+1+1+1+1. If we allow inverses as well, we can then get every element of the group from a single generator: the inverse of 1 is −1, so we can write (for example) −4=(−1)+(−1)+(−1)+(−1). (Including the inverses also means we don't need to include the identity, since for any g, gg−1=e.)
Por otro lado, para cualquier grupoG, we can certainly take G itself as a generating set! Then every element is considered a 'generator,' so every element can be written as a (trivial) product of generators. This tells us that for any group we can find a generating set. Usually, we try to find a generating set as small as possible. Sometimes, though, a larger generating set might be interesting if it helps us to better understand the group in question.
Una vez que tenemos un grupo generador para una gráficaG, we can produce a very nice visualization of the group called the Cayley graph. By graph, we mean a number of points (called vertices) connected by some arrows (called edges). Graphs are good for keeping track of relationships between things, and appear in many, many places in mathematics and in applications.
La gráfica Cayley de un grupo tiene un vértice por cada elementox in the group. Each vertex has one arrow coming out of it for each generator g, pointing to the element gx. (This creates the left Cayley graph. The right Cayley graph has arrows pointing from x to xg.) Usually we make the arrows different colors to correspond to the different generators; this is very useful for being able to visualize the structure of the group!
Para el grupo diedro, encontramos un conjunto de generadores con dos elementos: la rotación y el volteo sobre uno de los ejes. De hecho, ¡el grupo diedro tiene muchos conjuntos diferentes de generadores de tamaño dos! Podríamos haber elegido la rotación en sentido horario en lugar de la rotación en sentido antihorario, por ejemplo. O podríamos haber elegido cualquiera de los otros volteretas. Pero la gráfica Cayley resultante habría sido más o menos la misma.
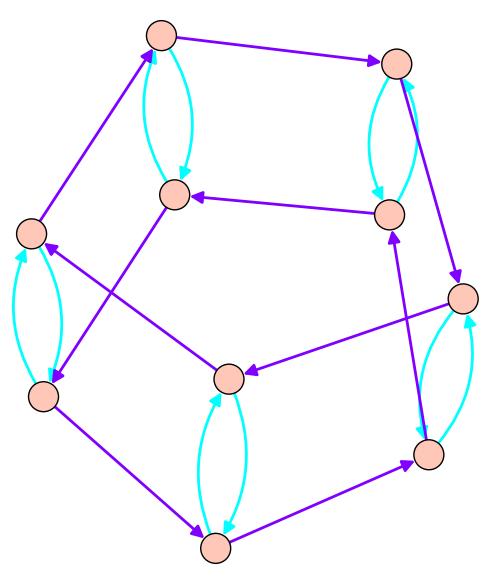
Figura 3.1: Gráfica de Cayley de grupo diedro, generada por volteo y rotación.
Un conjunto bastante diferente de generadores para el grupo diedro es tomar dos volteretas diferentes, a través de ejes adyacentes entre sí. Vamos a llamarlosf1 and f2. You can actually still write any element of the dihedral group as a product of these two flips. And the resulting Cayley graph looks quite different.
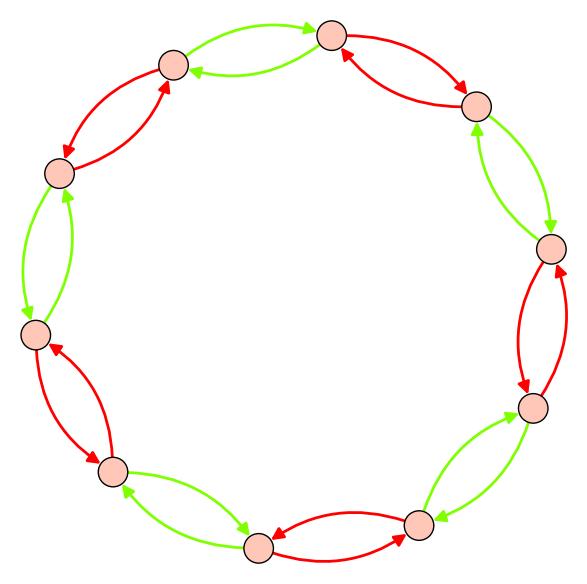
Figura 3.2: La gráfica Cayley para el grupo diedro con generadores dados por dos volteretas diferentes.
Supongamos que tenemos un generador dondeg2=1. It's tedious to draw arrows in both directions from every element, so we sometimes omit the arrow heads in this case.
Identificar generadores para el grupo de permutaciónS3. Make a Cayley graph.


