3.2: Visualización de Grupos- Cayley Graph
( \newcommand{\kernel}{\mathrm{null}\,}\)
Hasta ahora, hemos visto tres tipos diferentes de grupos: Grupos de simetrías (incluyendo el grupo diedro de simetrías de un polígono), los enteros módulon, and the permutation group, Sn. We've seen Cayley graphs for the dihedral group; let's see some Cayley graphs for some others.
Enteros Modulon
El módulo de enterosn only require a single generator to obtain the entire group. 1 is a nice choice of generator, as we know that every number k in {0,1,2,…n} can be written as k⋅1, which is to say, the sum of 1 with itself k times. The Cayley graph for this situation is simple: it's just n vertices, arranged in a loop with an arrow pointing from each number to the next. This creates a cycle! When n=8, the cycle is this: 0→1→2→3→4→5→6→7→0
Podemos elegir otros números que1 as the generator, though! Take n=8, and consider the number 3. We can make our Cayley graph by drawing a vertex for each number in {0,1,2,…,8} and an arrow from each x to x+3. Then the cycle draws out as: [0\rightarrow 3\rightarrow 6\rightarrow 1\rightarrow 4\rightarrow 7\rightarrow 2\rightarrow 5\rightarrow 0].
Aquí hay un gráfico de Cayley paraZ7 shown with three generators. Any one of the three generators would work just fine. The red vertex is the identity, 0. The green arrows are for the generator 1, blue for the generator 2, and green for the generator 3. What would happen if we included the generators 4,5, or 6?
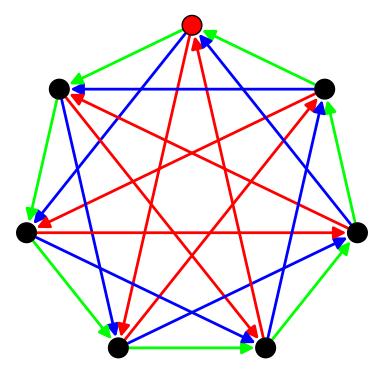
Figura 3.1: Gráfica de Cayley paraZ7 with three different generators. The identity is marked as the red dot.
Not every number is a generator of Zn. For example, in Z8, if we choose 4, the cycle is just: 0→4→0. Since the cycle doesn't contain every element of the group, we see that 4 doesn't generate the group on its own.
Suppose k∈Zn. Show that k generates Zn if and only if k is relatively prime to n. (ie, the only common divisor of k and n is 1.)
Suppose k∈Zn and k is not relatively prime to n. Is it possible to find another umber m not relatively prime to n such that k and m together generate Zn? Try some examples! Explain why or why not
Permutation Groups
The permutation group Sn has a number of interesting generating sets. We'll show a few of these generating sets for n=3 and n=4 for easy comparison.
The first generating set is a minimal set, using just two generators. The first generator is the 'rotation' with list notation r=[n,1,2,3,4,…,n−1]. The second is a flip, exchanging only the first two things, f=[2,1,3,4,…,n].
To check that these actually generate Sn, we need to see that we can construct an arbitrary permutation using just these generators. So consider an arbitrary permutation σ, written in list notation. If there are two adjacent entries that are out of order (big to the left of the small), we can apply rotations until the two things sit in the first two entries (suppose we use k rotations to do this). Then we apply the flip. And then we 'unrotate' k times to put the now-sorted numbers back. Then we find two more adjacent numbers and repeat. Once there are no adjacent numbers out of order, then we must be at the identity! Then the reverse of the sequence of moves we just made builds the permutation we wanted. Since the permutation was arbitrary, our two moves must generate the group.
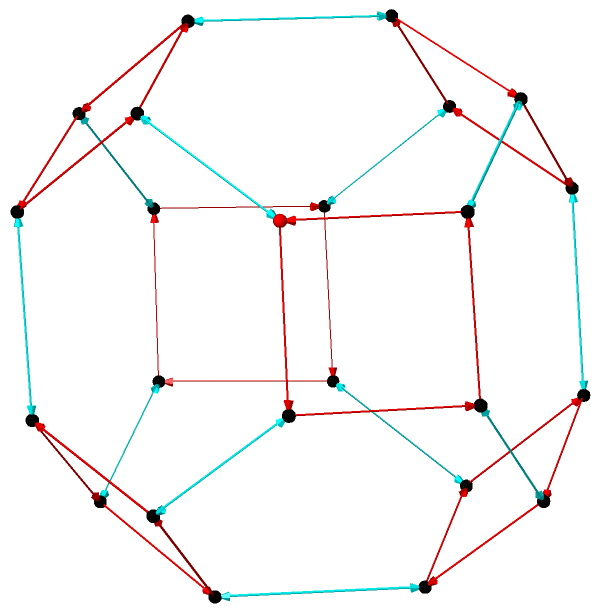
Figura 3.2: Un gráfico de Cayley paraS4, generated by the rotation [4,1,2,3] (in red) and reflection \([2,1,3,4]) (cyan).
Un segundo conjunto de generadores viene dado por el conjunto de todas las transposiciones. Estas son todas las permutaciones que tienen dos cosas cambiadas y todo lo demás en orden. Por ejemplo,[4,2,3,1] and [1,2,6,4,5,3] are transpositions. Modifying the above argument, you can see that the set of all transpositions are a generating set. There are more than 2 transpositions, so this isn't a minimal generating set. But it is an interesting set of generators when studying the permutation group more closely.
| Ejercicio 3.1.2 |
|---|
| ¿Cuántas transposiciones hay enSn? |
Sin embargo, un tercer conjunto de generadores viene dado por las simples transposiciones. Este es el conjunto de transposiciones{si} that just exchange i and i+1 while leaving everything else alone. There are n−1 simple transpositions. This is a very important set of generators in the further study of permutations! But it shows up in one simple context, as well.