5.2: Ejemplos de grupos de cocientes
- Page ID
- 111058
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Ahora que hemos aprendido un poco sobre los subgrupos y cocientes normales, deberíamos construir más ejemplos.
Enteros mod\(n\), Again
Recordemos al grupo\(\mathbb{Z}_n\). ¡Esto también se puede realizar como el grupo cociente!
Let\(n\mathbb{Z}\) denote the set of integers divisible by \(n\): \(n\mathbb{Z}=\{\ldots, -3n, -2n, -n, 0, n, 2n, 3n, \ldots\}\). This forms a subgroup: \(0\) is always divisible by \(n\), and if \(a\) and \(b\) are divisible by \(n\), then so is \(a+b\). Since every subgroup of a commutative group is a normal subgroup, we can from the quotient group \(\mathbb{Z}/\mathord n\mathbb{Z}\).
Para ver esto concretamente, vamos\(n=3\). Then the cosets of \(3\mathbb{Z}\) are \(3\mathbb{Z}\), \(1+3\mathbb{Z}\), and \(2+3\mathbb{Z}\). We can then add cosets, like so: \((1+3\mathbb{Z}) + (2+3\mathbb{Z}) = 3+3\mathbb{Z} = 3\mathbb{Z}.\) The last equality is true because \(3\mathbb{Z}=\{\ldots, -6, -3, 0, 3, 6, \ldots\}\), so that \(3+3\mathbb{Z}=\{\ldots, -3, 0, 3, 6, 9, \ldots\}=3\mathbb{Z}\).
El Grupo Alternante
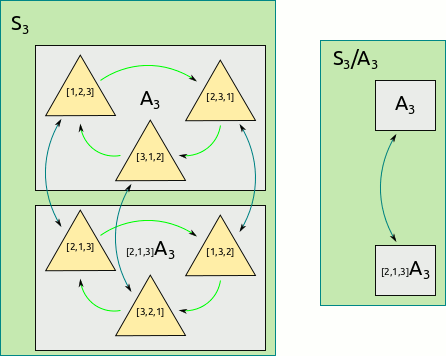
Otro ejemplo es un subgrupo muy especial del grupo simétrico llamado el grupo Alternante,\(A_n\). Hay un par de formas diferentes de interpretar el grupo alterno, pero principalmente se reduce a la idea del signo de una permutación, que es siempre\(\pm 1\). El conjunto\(\{1, -1\}\) forma un grupo bajo multiplicación, isomórfico a\(\mathbb{Z}_2\). El signo de una permutación es en realidad un homomorfismo. Existen numerosas formas de calcular el signo o una permutación:
- Determinantes. Una matriz de permutación es la matriz de la transformación lineal de\(n\)-dimensional space sending the \(i\)-th coordinate vector \(e_i\) to \(e_{\sigma(i)}\). Such matrices have entries all equal to zero or one, with exactly one 1 in each row and each column. One can easily show that such a matrix has determinant equal to \(\pm 1\). Since the determinant is a multiplicative function - \(\det (MN) = \det(M) \det(N)\) - we can observe the the determinant is a homomorphism from the group of permutation matrices to the group \(\{\pm 1\}\).
- Contar inversiones. Una inversión en una permutación\(\sigma\) is a pair \(i<j\) with \(\sigma(i)>\sigma(j)\). For example, the permutation \([3,1,4,2]\) has \(\sigma(1)>\sigma(2), \sigma(1)>\sigma(3)\) and \(\sigma(3)>\sigma(4)\), and thus has three inversions. If there are \(i\) inversions, then the sign of the permutation is \((-1)^i\).
- Contar cruces. Dibuja una notación trenzada para la permutación donde no se crucen más de dos líneas en ningún punto y ninguna línea se intersecta a sí misma. Luego cuente el número de cruces,\(c\). Then \(s(\sigma)=(-1)^{c}\). The alternating group is the subgroup of \(S_n\) with \(s(\sigma)=1\). (To prove that this method of counting works, one needs a notion of Reidemeister moves, which originally arise in the fascinating study of mathematical knots.)
Llamamos a una permutación con signo\(+1\) a positive permutation, and a permutation with sign \(-1\) a negative permutation.
Ahora podemos definir el grupo alterno.
El grupo alterno\(A_n\) is the kernel of the homomorphism \(s: S_n\rightarrow \mathbb{Z}_2\). Equivalently, \(A_n\) is the subgroup of all positive permutations in \(S_n\).
De hecho, el grupo alterno tiene exactamente dos cosets. El grupo cociente\(S_n/\mathord A_n\) is then isomorphic to \(\mathbb{Z}_2\).
