6.1: Productos de Grupos
- Page ID
- 117736
En esta sección, discutiremos un método para usar grupos existentes como bloques de construcción para formar nuevos grupos.
Supongamos\((G,*)\) y\((H,\odot)\) son dos grupos. Recordemos que el producto cartesiano de\(G\) y\(H\) se define como\[G\times H=\{(g,h)\mid g\in G,h\in H\}\] Usando las operaciones binarias para los grupos\(G\) y\(H\), podemos definir una operación binaria en el conjunto\(G\times H\). Definir\(\star\) en\(G\times H\) via\[(g_1,h_1)\star(g_2,h_2)=(g_1*g_2,h_1\odot h_2).\] Esto se ve más elegante de lo que es. Sólo estamos haciendo la operación de cada grupo en el componente apropiado. Resulta que\((G\times H,\star)\) es un grupo.
Supongamos\((G,*)\) y\((H,\odot)\) son dos grupos, donde\(e\) y\(e'\) son los elementos de identidad de\(G\) y\(H\), respectivamente. Entonces\((G\times H,\star)\) es un grupo, donde\(\star\) se define como arriba. Además,\((e,e')\) es la identidad de\(G\times H\) y la inversa de\((g,h)\in G\times H\) viene dada por\((g,h)^{-1}=(g^{-1},h^{-1})\).
Nos referimos\(G\times H\) como el producto directo de los grupos\(G\) y\(H\). En este caso, cada uno de\(G\) y\(H\) se llama factor del producto directo. A menudo abreviamos\((g_1,h_1)\star(g_2,h_2)=(g_1*g_2,h_1\odot h_2)\) por\((g_1,h_1)(g_2,h_2)=(g_1 g_2,h_1 h_2)\). Una excepción a esto es si estamos usando la operación de adición en cada componente. Por ejemplo, considere\(\mathbb{Z}_4\times \mathbb{Z}_2\) bajo la operación de adición mod 4 en el primer componente y adición mod 2 en el segundo componente. Entonces\[\mathbb{Z}_4 \times \mathbb{Z}_2=\{(0,0),(1,0),(2,0),(3,0),(0,1),(1,1),(2,1),(3,1)\}.\] En este caso, usaremos notación aditiva en\(\mathbb{Z}_4\times \mathbb{Z}_2\). Por ejemplo, en\(\mathbb{Z}_4 \times \mathbb{Z}_2\) tenemos\[(2,1)+(3,1)=(1,0)\] y\[(1,0)+(2,1)=(3,1).\] Por otra parte, la identidad del grupo es\((0,0)\). A modo de ejemplo, la inversa de\((1,1)\) es\((3,1)\) since\((1,1)+(3,1)=(0,0)\). Hay un conjunto generador muy natural para\(\mathbb{Z}_4\times \mathbb{Z}_2\), es decir,\(\{(1,0),(0,1)\}\) desde\(1\in \mathbb{Z}_4\) y\(1\in \mathbb{Z}_2\) generar\(\mathbb{Z}_4\) y\(\mathbb{Z}_2\), respectivamente. El diagrama Cayley correspondiente se da en la Figura\(\PageIndex{1}\).
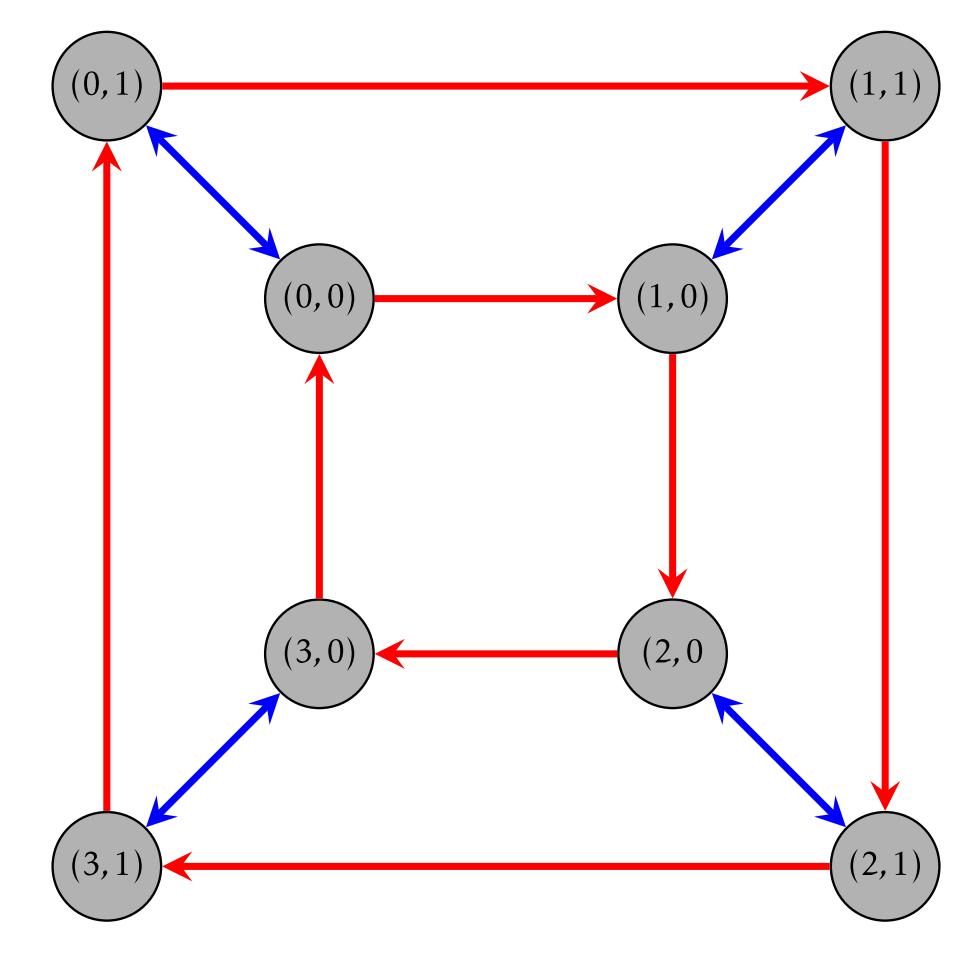
Considera al grupo\(\mathbb{Z}_4 \times \mathbb{Z}_2\). ¿Este grupo es abeliano? ¿El grupo es cíclico? Determinar si\(\mathbb{Z}_4 \times \mathbb{Z}_2\) es isomórfico a cualquiera de\(D_4\),\(Q_8\),\(\mathbb{Z}_8\), o\(L_3\).
El resultado del problema anterior es que hay al menos cinco grupos de orden 8 hasta el isomorfismo. Resulta que hay exactamente cinco grupos de orden 8 hasta el isomorfismo. En particular, cada grupo del orden 8 es isomórfico a uno de los siguientes grupos:\(\mathbb{Z}_8\),\(\mathbb{Z}_4 \times \mathbb{Z}_2\),\(L_3\),\(D_4\), y\(Q_8\). Tenga en cuenta que\(R_8\cong \mathbb{Z}_8\) y\(\text{Spin}_{1\times 2}\cong D_4\). Tres de las clases de isomorfismo corresponden a grupos abelianos mientras que las otras dos corresponden a grupos no abelianos. Desafortunadamente, no desarrollaremos las herramientas necesarias para demostrar que esta clasificación está completa.
Los dos teoremas siguientes no deberían ser terriblemente sorprendentes.
Si\(G_1\) y\(G_2\) son grupos, entonces\(G_1\times G_2\cong G_2\times G_1\).
Supongamos\(G_1\) y\(G_2\) son grupos con identidades\(e_1\) y\(e_2\), respectivamente. Entonces\(\{e_1\}\times G_2\cong G_2\) y\(G_1\times \{e_2\}\cong G_1\).
No hay razón por la que no podamos tomar el producto directo de más de dos grupos. Si\(A_1, A_2, \ldots, A_n\) es una colección de conjuntos, definimos\[\prod_{i=1}^nA_i:=A_1\times A_2\times \cdots \times A_n.\] Cada elemento de\(\prod_{i=1}^nA_i\) es de la forma\((a_1,a_2,\ldots, a_n)\), donde\(a_i\in A_i\).
\(G_1, G_2,\ldots, G_n\)Dejen ser grupos. Para\((a_1,a_2, \ldots, a_n), (b_1,b_2,\ldots, b_n)\in \prod_{i=1}^nG_i\), definir\[(a_1,a_2, \ldots, a_n)(b_1,b_2,\ldots, b_n)=(a_1b_1,a_2b_2,\ldots, a_nb_n).\] Entonces\(\prod_{i=1}^nG_i\), el producto directo de\(G_1,\ldots, G_n\), es un grupo bajo esta operación binaria.
Una forma de pensar sobre los productos directos es que podemos navegar por el producto navegando por cada factor simultáneamente pero independientemente. Calcular el orden de un grupo que es un producto directo es sencillo.
\(G_1, G_2,\ldots, G_n\)Dejen ser grupos finitos. Entonces\[|G_1\times G_2\times \cdots \times G_n|=|G_1|\cdot|G_2|\cdots |G_n|.\]
\(G_1, G_2,\ldots, G_n\)Dejen ser grupos. Entonces\(|G_1\times G_2\times \cdots \times G_n|\) es infinito si y sólo si al menos uno\(|G_i|\) es infinito.
Debe quedar claro el siguiente teorema.
\(G_1, G_2,\ldots, G_n\)Dejen ser grupos. Entonces\(\prod_{i=1}^nG_i\) es abeliano si y sólo si cada uno\(G_i\) es abeliano.
Juguemos con algunos ejemplos más.
Dibuja el diagrama de Cayley para\(\mathbb{Z}_2\times \mathbb{Z}_3\) usarlo\(\{(1,0),(0,1)\}\) como conjunto generador. ¿Es\(\mathbb{Z}_2\times \mathbb{Z}_3\) un grupo abeliano? ¿Es cíclico? ¿A qué grupo familiar es\(\mathbb{Z}_2\times \mathbb{Z}_3\) isomórfico?
Considera\(\mathbb{Z}_2\times \mathbb{Z}_2\) bajo la operación de adición mod 2 en cada componente. Encuentre un conjunto generador para\(\mathbb{Z}_2\times \mathbb{Z}_2\) y luego cree un diagrama de Cayley para este grupo. ¿A qué grupo conocido es\(\mathbb{Z}_2\times \mathbb{Z}_2\) isomórfico?
Considere las similitudes y diferencias entre\(\mathbb{Z}_2\times \mathbb{Z}_3\) y\(\mathbb{Z}_2\times \mathbb{Z}_2\). Ambos grupos son abelianos por teorema\(\PageIndex{7}\), pero sólo el primero es cíclico. Aquí hay otro ejercicio.
Considera al grupo\(\mathbb{Z}_2 \times \mathbb{Z}_2 \times \mathbb{Z}_2\). Encuentre un conjunto generador para\(\mathbb{Z}_2 \times \mathbb{Z}_2 \times \mathbb{Z}_2\) y luego cree un diagrama de Cayley para este grupo. ¿Hay algún grupo que hayamos visto antes que\(\mathbb{Z}_2 \times \mathbb{Z}_2 \times \mathbb{Z}_2\) isomórfico a?
El siguiente teorema nos dice cómo calcular el orden de un elemento en un producto directo de grupos.
Supongamos que\(G_1, G_2,\ldots, G_n\) son grupos y vamos\((g_1,g_2,\ldots, g_n)\in \prod_{i=1}^nG_i\). Si\(|g_i|=r_i<\infty\), entonces\(|(g_1,g_2,\ldots, g_n)|=\text{lcm}(r_1,r_2,\ldots,r_n)\).
Encuentra el orden de cada uno de los siguientes elementos.
- \((6,5)\in\mathbb{Z}_{12}\times \mathbb{Z}_7\).
- \((r,i)\in D_3\times Q_8\).
- \(((1,2)(3,4),3)\in S_4\times \mathbb{Z}_{15}\).
Encuentra el mayor orden posible de elementos en cada uno de los siguientes grupos.
- \(\mathbb{Z}_6\times \mathbb{Z}_8\)
- \(\mathbb{Z}_9\times \mathbb{Z}_{12}\)
- \(\mathbb{Z}_4\times \mathbb{Z}_{18}\times \mathbb{Z}_{15}\)
El grupo\(\mathbb{Z}_m\times \mathbb{Z}_n\) es cíclico si y solo si\(m\) y\(n\) son relativamente primos.
El grupo\(\mathbb{Z}_m\times \mathbb{Z}_n\) es isomórfico a\(\mathbb{Z}_{mn}\) si y solo si\(m\) y\(n\) son relativamente primos.
Los resultados anteriores pueden extenderse a más de dos factores.
El grupo\(\prod_{i=1}^n \mathbb{Z}_{m_i}\) es cíclico e isomórfico a\(\mathbb{Z}_{m_1m_2\cdots m_n}\) si y solo si cada par de la colección\(\{m_1,m_2,\ldots, m_n\}\) es relativamente primo.
Determinar si cada uno de los siguientes grupos es cíclico.
- \(\mathbb{Z}_7\times \mathbb{Z}_8\)
- \(\mathbb{Z}_7\times \mathbb{Z}_7\)
- \(\mathbb{Z}_2\times \mathbb{Z}_7\times \mathbb{Z}_8\)
- \(\mathbb{Z}_5\times \mathbb{Z}_7\times \mathbb{Z}_8\)
Supongamos\(n=p_1^{n_1}p_2^{n_2}\cdots p_r^{n_r}\), donde cada uno\(p_i\) es un número primo distinto. Entonces\[\mathbb{Z}_n\cong \mathbb{Z}_{p_1^{n_1}}\times \mathbb{Z}_{p_2^{n_2}}\times \cdots \times \mathbb{Z}_{p_r^{n_r}}.\]
El siguiente teorema nos dice que el producto directo de los subgrupos es siempre un subgrupo.
Supongamos\(G_1\) y\(G_2\) son grupos tales que\(H_1\leq G_1\) y\(H_2\leq G_2\). Entonces\(H_1\times H_2\leq G_1\times G_2\).
Sin embargo, no todos los subgrupos de un producto directo tienen la forma anterior.
Encuentra un ejemplo que ilustre que no todos los subgrupos de un producto directo son producto directo de subgrupos de los factores.
¿Podemos extender el teorema\(\PageIndex{12}\) a los subgrupos normales? Es decir, si\(H_1\trianglelefteq G_1\) y\(H_2\trianglelefteq G_2\), ¿es así\(H_1\times H_2\trianglelefteq G_1\times G_2\)? Si es así, probarlo. De lo contrario, proporcione un contraejemplo.
El siguiente teorema describe con precisión la estructura de los grupos abelianos finitos. Omitiremos su prueba, pero nos permitiremos utilizarla según sea necesario.
Cada grupo abeliano finitamente generado\(G\) es isomórfico a un producto directo de grupos cíclicos de la forma\[\mathbb{Z}_{p_1^{n_1}}\times \mathbb{Z}_{p_2^{n_2}}\times \cdots \times \mathbb{Z}_{p_r^{n_r}}\times \mathbb{Z}^k,\] donde cada uno\(p_i\) es un número primo (no necesariamente distinto). El producto es único hasta el reordenamiento de los factores.
Tenga en cuenta que el número\(k\) se llama el número Betti. Un grupo abeliano finitamente generado es finito si y solo si el número Betti es 0.
Encuentra todos los grupos abelianos hasta isomorfismo de orden 8. ¿Cuántos grupos diferentes hasta el isomorfismo (tanto abeliano como no abeliano) hemos visto y cuáles son?
Encuentra todos los grupos abelianos hasta isomorfismo para cada uno de los siguientes órdenes.
- 16
- 12
- 25
- 30
- 60


