6.2: Cocientes de Grupos

En la sección anterior, discutimos un método para construir grupos “más grandes” a partir de grupos “más pequeños” usando una construcción directa de productos. En esta sección, en cierto sentido haremos lo contrario.

Problema 5.3.2 insinuó que si\(H\leq G\) y organizamos la tabla de grupo de acuerdo con los cosets izquierdos de\(H\), entonces la tabla de grupo tendrá patrón de tablero de ajedrez si y solo si\(H\) es normal en G (es decir, los cosets izquierdo y derecho de \(H\)son los mismos). Por ejemplo, consulta la tabla coloreada anterior a Problema 5.1.2 versus las que creaste en Ejercicios 5.1.2, 5.1.3. Si tenemos el patrón de tablero de ajedrez en la tabla de grupo que surge de un subgrupo normal, entonces al “pegar” los bloques coloreados, obtenemos una tabla de grupo para un grupo menor que tiene los cosets como elementos.

Por ejemplo, consideremos\(K=\langle -1\rangle \leq Q_8\). El problema 5.1.3 nos mostró que\(K\) es normal\(Q_8\). Los cosets izquierdo (y derecho) de\(K\) in\(Q_8\) son\[K=\{1,-1\}, iK=\{i,-i\}, jK=\{j,-j\}, \text{ and } kK=\{k,-k\}.\] Como encontraste en Problema 5.1.3, si organizamos las filas y columnas de\(Q_8\) según estos cosets, obtenemos la siguiente tabla de grupos.

Figura\(\PageIndex{1}\)

Si consideramos los\(2\times 2\) bloques como elementos, parece que tenemos una tabla de grupo para un grupo con 4 elementos. Una inspección más cercana revela que esto se parece a la mesa para\(V_4\). Si la tabla de\(2\times 2\) bloques va a representar un grupo, necesitamos entender la operación binaria. ¿Cómo “multiplicamos” los cosets? Por ejemplo, la tabla sugiere que el coset\(jK\) (coloreado en rojo) veces el coset\(iK\) (coloreado en azul) es igual a\(kK\) (coloreado en púrpura) a pesar de que\(ji=-k\neq k\). Sin embargo, es cierto que el producto\(ji=-k\) es un elemento en el coset\(kK\). De hecho, si miramos de cerca la mesa, vemos que si elegimos dos cosets cualesquiera, el producto de cualquier elemento del primer coset multiplicado por cualquier elemento del segundo coset siempre resultará en un elemento en el mismo coset independientemente de qué representantes elegimos.

En otras palabras, parece que podemos multiplicar cosets eligiendo a cualquier representante de cada coset y luego viendo en qué coset se encuentra el producto de los representantes. No obstante, es importante señalar que esto sólo funcionará si tenemos un patrón de tablero de ajedrez de cosets, lo que hemos visto evidencia de que solo sucede cuando el subgrupo correspondiente es normal.

Antes de continuar, sigamos retozando con el mismo ejemplo. Considere el diagrama Cayley para\(Q_8\) con generadores\(\{i,j,-1\}\) que se da en la Figura\(\PageIndex{2}\) a.

Figura\(\PageIndex{2}\): La subfigura izquierda muestra el diagrama de Cayley para\(Q_8\) con grupo generador\(\{i,j,-1\}\). La subfigura derecha muestra el diagrama de Cayley colapsado para\(Q_8\) según los coconjuntos izquierdos de\(K=\langle -1\rangle\).

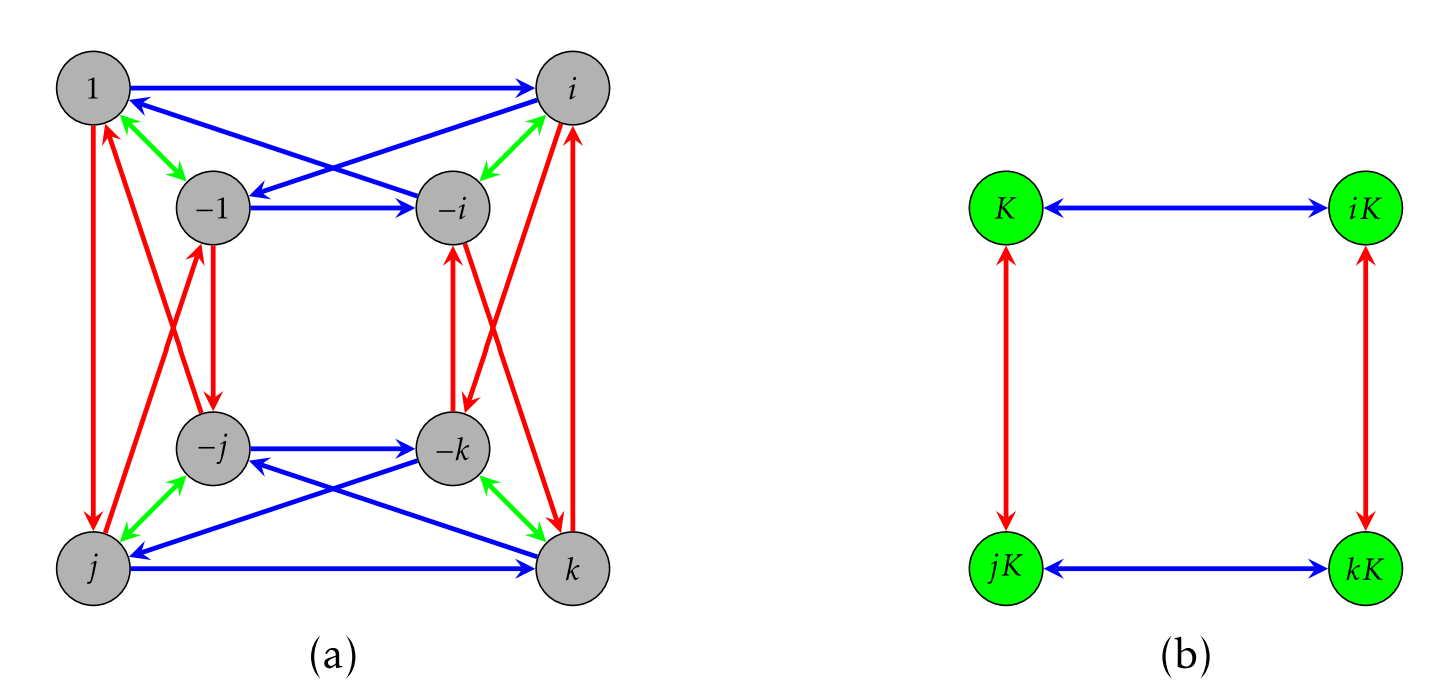
Podemos visualizar los coconjuntos correctos de\(K\) como los grupos de vértices conectados entre sí con las flechas verdes de dos vías. En este caso, también estamos viendo los cosets izquierdos ya que\(K\) es normal en\(Q_8\). Si colapsamos los cosets unos sobre otros y colapsamos las flechas correspondientes, obtenemos el diagrama dado en la Figura\(\PageIndex{2}\) (b). Es claro que este diagrama es el diagrama de Cayley para un grupo que es isomórfico a\(V_4\). Por razones que entenderemos en breve, este procesamiento de colapsar un diagrama de Cayley de acuerdo con los coconjuntos de un subgrupo normal se llama el “proceso de cociente”.

Problema\(\PageIndex{1}\): Bad Quotient

Veamos qué pasa si intentamos el proceso de cociente para un subgrupo que no es normal. Considerar\(H=\langle s\rangle \leq D_3\). En Problema 5.1.1, descubrimos que los cosets izquierdos de no\(H\) son los mismos que los cosets derechos de\(H\). Esto implica que no\(H\) es normal en\(D_3\). Considere el diagrama estándar de Cayley para\(D_3\) que utilice los generadores\(r\) y\(s\). Dibuja el diagrama que resulta de intentar el proceso de cociente al\(D_3\) usar el subgrupo\(H\). Explique por qué este diagrama no puede ser el diagrama de un grupo.

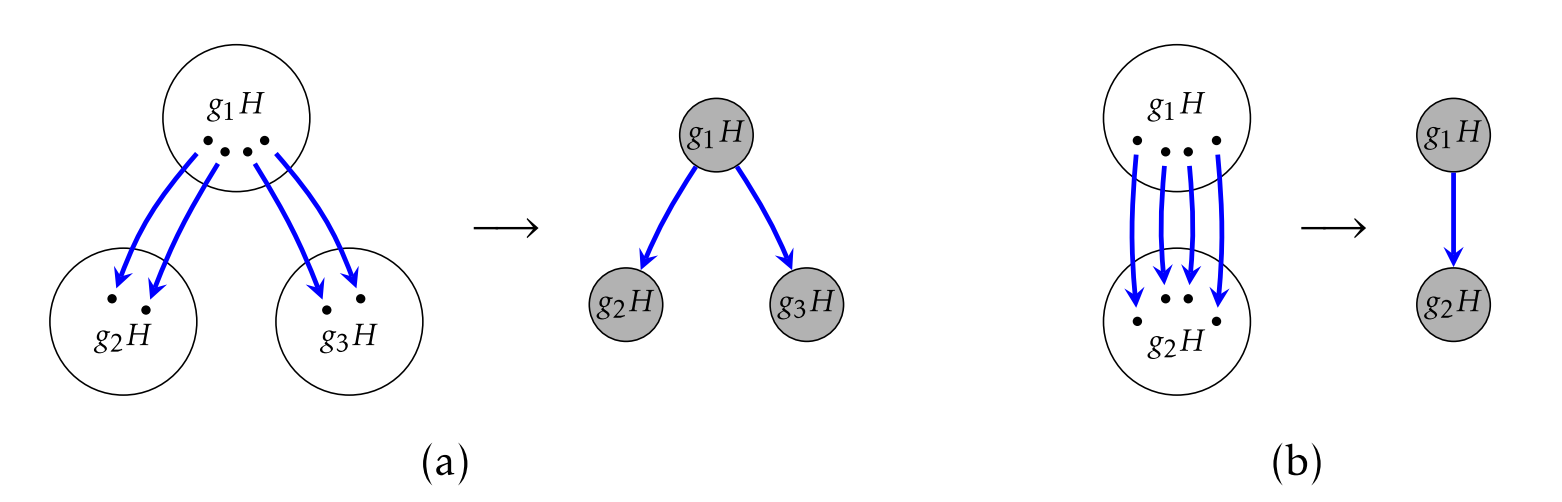
El problema que surge en Problem\(\PageIndex{1}\) es que si los mismos tipos de flecha (es decir, los que representan el mismo generador) que dejan un coset no apuntan a elementos en el mismo coset, intentar el proceso de cociente resultará en un diagrama que no puede ser un diagrama de Cayley para un grupo ya que tenemos más de uno flecha del mismo tipo dejando un vértice. En la Figura\(\PageIndex{3}\) a, ilustramos lo que sale mal si todas las flechas para un generador que señala de un coset no apuntan unánimemente a elementos del mismo coset. En la Figura\(\PageIndex{3}\) b, todas las flechas apuntan a elementos en un mismo coset, y en este caso, parece que todo sale bien.

Figura\(\PageIndex{3}\): En la subfigura izquierda, las flechas azules van de elementos del coconjunto izquierdo\(g_1H\) a elementos de múltiples coconjuntos izquierdos, lo que da como resultado flechas azules ambiguas en el diagrama colapsado. Esto implica que la multiplicación del coset izquierdo no está bien definida en este caso. En la subfigura derecha, las flechas azules van de elementos del coconjunto izquierdo\(g_1H\) a elementos dentro de un único coset izquierdo, lo que no da lugar a ninguna ambigüedad.

Problema\(\PageIndex{2}\)

En Problema 5.1.2, aprendimos que el subgrupo\(K=\langle r\rangle\) es normal en\(D_3\) ya que los coconjuntos izquierdos son iguales a los coconjuntos derechos. Tenga en cuenta que esto se desprende inmediatamente del Teorema 5.3.3 desde entonces\([D_3:K]=2\). Dibuja el diagrama que resulta de realizar el proceso de cociente a\(D_3\) usar el subgrupo\(K\). ¿El diagrama resultante representa un grupo? Si es así, ¿a qué grupo es isomórfico?

Ahora, supongamos que\(G\) es un grupo arbitrario y vamos\(H\leq G\). Considera el conjunto de cosets izquierdos de\(H\). Nosotros definimos\[(aH)(bH):=(ab)H.\] La pregunta natural a hacer es si esta operación está bien definida. Es decir, ¿depende de nuestra elección de representantes el resultado de multiplicar dos cosets de izquierda? Más específicamente, supongamos\(c\in aH\) y\(d\in bH\). Entonces\(cH=aH\) y\(dH=bH\). De acuerdo con la operación definida anteriormente,\((cH)(dH)=cdH\). Será mejor que\(cdH=abH\), de lo contrario la operación no esté bien definida.

Problema\(\PageIndex{3}\)

Vamos\(H=\langle s\rangle \leq D_3\). Encuentra ejemplos específicos de\(a,b,c,d\in D_3\) tales que\[(aH)(bH)\neq (cH)(dH)\] aunque\(aH=cH\) y\(bH=dH\).

Teorema\(\PageIndex{1}\)

Seamos\(G\) un grupo y vamos\(H\leq G\). Entonces la multiplicación del coset izquierdo (como se definió anteriormente) está bien definida si y solo si\(H\trianglelefteq G\).

Teorema\(\PageIndex{2}\):Quotient Group

Seamos\(G\) un grupo y vamos\(H\trianglelefteq G\). Después el conjunto de cosets izquierdos de\(H\) en\(G\) forma un grupo bajo multiplicación de coset izquierdo.

El grupo del Teorema\(\PageIndex{2}\) se denota por\(G/H\), se lee\(H\) “\(G\)mod “, y se conoce como el grupo cociente (o grupo factor) de\(G\) by\(H\). Si\(G\) es un grupo finito, entonces\(G/H\) es exactamente el grupo que surge de “pegar” los bloques de colores en una tabla de grupo con patrón de tablero de ajedrez. También es el grupo que obtenemos después de aplicar el proceso de cociente al diagrama de Cayley. Es importante señalar una vez más que esto sólo funciona correctamente si\(H\) es un subgrupo normal.

Recordemos que el Teorema [THM:ABELIANIMPLIESNormal] nos dice que si\(G\) es abeliano, entonces cada subgrupo es normal. Esto implica que cuando\(G\) es abeliano,\(G/H\) es un grupo bien definido para cada subgrupo\(H\) de\(G\). Sin embargo, no es\(G\) necesario ser abeliano\(G/H\) para ser un grupo bien definido. El grupo cociente\(Q_8/\langle -1\rangle\) es un ejemplo donde esto sucede.

El siguiente teorema nos dice cómo calcular el orden de un grupo de cocientes.

Teorema\(\PageIndex{3}\)

Seamos\(G\) un grupo y vamos\(H\trianglelefteq G\). Entonces\(|G/H|=[G:H]\). En particular, si\(G\) es finito, entonces\(|G/H|=|G|/|H|\).

Es importante señalar que el orden de un grupo de cocientes puede ser finito aunque\(G\) tenga un orden infinito.

Problema\(\PageIndex{4}\)

Considera al grupo\((\mathbb{Z},+)\). Ya que\(\mathbb{Z}\) es abeliano, cada subgrupo es normal. Por ejemplo,\(4\mathbb{Z} \trianglelefteq \mathbb{Z}\), lo que implica que\(\mathbb{Z}/4\mathbb{Z}\) es un grupo cociente bien definido. Además, ambos\(\mathbb{Z}\) y\(4\mathbb{Z}\) tienen orden infinito. ¿A qué es\(|\mathbb{Z}/4\mathbb{Z}|\) igual? ¿Se puede determinar a qué grupo conocido\(\mathbb{Z}/4\mathbb{Z}\) es isomórfico?

Supongamos que\(G\) es un grupo y\(H\trianglelefteq G\), entonces ese\(G/H\) es un grupo. Recordemos que los elementos del grupo\(G/H\) son los cosets izquierdos de\(H\), que son de la forma\(aH\) donde\(a\in G\). El funcionamiento del grupo se define vía\[(aH)(bH) = abH.\] Además, la identidad en\(G/H\) es\(eH = H\) since\((aH)(eH) = aH\). Por Corolario 4.1.2\(|aH| = k\) si y solo\((aH)^k = H\) y\(k\) es el menor exponente positivo de este tipo con esta propiedad. Pero fíjense en eso\((aH)^k = a^kH\). Entonces, para poder calcular el orden de\(aH\), necesitamos encontrar el exponente positivo más pequeño\(k\) tal que\(a^kH = H\), pero\(a^kH = H\) exactamente cuando\(a^k\) está en\(H\). El resultado es que para encontrar el orden de\(aH\) in\(G/H\), necesitamos el más pequeño positivo\(k\) tal que\(a^k\) esté en\(H\).

Problema\(\PageIndex{5}\)

Encuentra el orden del elemento dado en el grupo de cocientes. Se puede suponer que estamos tomando el cociente por un subgrupo normal.

1. \(s\langle r\rangle \in D_4/\langle r\rangle\)
2. \(j\langle -1\rangle \in Q_8/\langle -1\rangle\)
3. \(5+\langle 4\rangle \in \mathbb{Z}_{12}/\langle 4\rangle\)
4. \((2,1)+\langle (1,1)\rangle \in (\mathbb{Z}_3\times \mathbb{Z}_6)/\langle (1,1)\rangle\)
5. \((1,3)+\langle (0,2)\rangle\in (\mathbb{Z}_4\times \mathbb{Z}_8)/\langle (0,2)\rangle\)

Problema\(\PageIndex{6}\)

Para cada grupo de cociente a continuación, describa el grupo. Si es posible, indicar a qué grupo es isomórfico cada uno. Se puede suponer que estamos tomando el cociente por un subgrupo normal.

1. \(Q_8/\langle -1\rangle\)
2. \(Q_8/\langle i\rangle\)
3. \(\mathbb{Z}_4/\langle 2\rangle\)
4. \(V_4/\langle h\rangle\)
5. \(A_4/\langle (1,2)(3,4),(1,3)(2,4)\rangle\)
6. \((\mathbb{Z}_2\times \mathbb{Z}_2)/\langle (1,1)\rangle\)
7. \(\mathbb{Z}/4\mathbb{Z}\)
8. \(S_4/A_4\)
9. \((\mathbb{Z}_4\times \mathbb{Z}_2)/(\{0\}\times \mathbb{Z}_2)\)

Problema\(\PageIndex{7}\)

Computar el orden de cada elemento en el grupo de cocientes\((\mathbb{Z}_2\times \mathbb{Z}_4)/\langle (0,2)\rangle\). ¿A qué grupo conocido es\((\mathbb{Z}_2\times \mathbb{Z}_4)/\langle (0,2)\rangle\) isomórfico?

Teorema\(\PageIndex{4}\)

Seamos\(G\) un grupo. Entonces

1. \(G/\{e\}\cong G\)
2. \(G/G\cong \{e\}\)

Teorema\(\PageIndex{5}\)

Tenemos lo siguiente.

1. Para\(n\geq 2\),\(S_n/A_n\cong \mathbb{Z}_2\).
2. Para todos\(n\in\mathbb{N}\),\(\mathbb{Z}/n\mathbb{Z}\cong \mathbb{Z}_n\).
3. Para todos\(n\in\mathbb{N}\),\(\mathbb{R}/n\mathbb{R}\cong \{e\}\).

Teorema\(\PageIndex{6}\)

Seamos\(G\) un grupo y vamos\(H\trianglelefteq G\). Si\(G\) es abeliano, entonces también lo es\(G/H\).

Problema\(\PageIndex{8}\)

Demostrar que lo contrario del teorema anterior no es cierto al proporcionar un contraejemplo específico.

Problema\(\PageIndex{9}\)

Consideremos el grupo cociente\((\mathbb{Z}_4\times \mathbb{Z}_6)/\langle (0,1)\rangle\).

1. ¿Cuál es el orden de\((\mathbb{Z}_4\times \mathbb{Z}_6)/\langle (0,1)\rangle\)?
2. ¿El grupo es abeliano? ¿Por qué?
3. Anota todos los elementos de\((\mathbb{Z}_4\times \mathbb{Z}_6)/\langle (0,1)\rangle\).
4. ¿Uno de los elementos genera el grupo?
5. ¿A qué grupo conocido es\((\mathbb{Z}_4\times \mathbb{Z}_6)/\langle (0,1)\rangle\) isomórfico?

Teorema\(\PageIndex{7}\)

Seamos\(G\) un grupo y vamos\(H\trianglelefteq G\). Si\(G\) es cíclico, entonces también lo es\(G/H\).

Problema\(\PageIndex{10}\)

Demostrar que lo contrario del teorema anterior no es cierto al proporcionar un contraejemplo específico.

Aquí hay algunos ejercicios adicionales. Estos son un poco más duros.

Problema\(\PageIndex{11}\)

Para cada grupo de cociente a continuación, describa el grupo. Si es posible, indicar a qué grupo es isomórfico cada uno. Se puede suponer que estamos tomando el cociente por un subgrupo normal.

1. \((\mathbb{Z}_4\times \mathbb{Z}_6)/\langle (0,2)\rangle\)
2. \((\mathbb{Z}\times \mathbb{Z})/\langle (1,1)\rangle\)
3. \(\mathbb{Q}/\langle 1\rangle\)(la operación en\(\mathbb{Q}\) es adición)