3.0: Preludio a transformaciones lineales y álgebra matricial

Última actualización
Guardar como PDF

Page ID: 113097

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Ejemplo$\PageIndex{1}$

Supongamos que está construyendo un brazo robot con tres articulaciones que pueden mover su mano alrededor de un plano, como en la siguiente imagen.

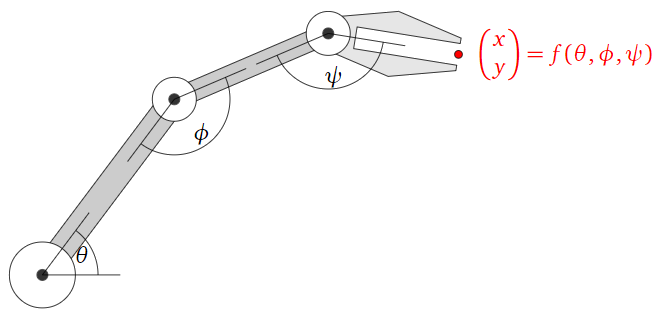
$162682942668943594.png$

Figura$\PageIndex{1}$

23 de Jun de 2021 12:13

\ usetikzlibrary {ipe}\ usetikzlibrary {ángulos}\ tikzstyle {ipe stylesheet} = [importación de ipe, regla par impar, unión de línea=redondo, tapa de línea=trasero, pluma ipe normal/.style= {ancho de línea=0.4}, ipe pen pesado/.style= {line width=0.8}, ipe pen fat/style.= {line width=1.2}, ipe pen ultrafat/.style= {line width=2}, ipe pen normal, ipe mark normal/.style= {ipe mark scale=3}, ipe mark grande/.style= {ipe mark scale=5}, ipe mark small/.style= {ipe mark scale=2}, ipe mark tiny/.style= {ipe mark scale=1.1}, ipe mark normal, /pgf/teclas de flecha/.cd, ipe flecha normal/.style= {e=7}, ipe flecha grande/.style= {scale=10}, ipe flecha pequeña/.style= {scale=5}, ipe flecha tiny/.style= {scale=3}, ipe flecha normal, /tikz/.cd, flechas ipe,% flechas de actualización <->/.tip = ipe normal, ipe dash normal/.style= {dash pattern=}, ipe dash rayado/.style= {dash pattern=on 4bp off 4bp}, ipe dash dotted/.style= {dash pattern=on 1bp off 3bp}, ipe dash dash punteado/.style= {dash pattern=on 4bp off 2 bp on 1bp off 2bp}, ipe dash dot dot dotado/.style= {dash pattern=on 4bp off 2bp on 1bp off 2bp on 1bp off 2bp off 2bp}, ipe dash normal, ipe node/.append style= {font=\ normalsize}, ipe stretch normal/.style= {ipe node stretch=1}, ipe stretch normal, ipe opacidad 10/..estilo= {opacidad=0.1}, opacidad ipe 30/.style= {opacity=0.3}, opacidad ipe 50/.style= {opacity=0.5}, opacidad ipe 75/.style= {opacity=0.75}, opacidad ipe opaque/.style= {opacity=1}, opacidad ipe opaca,]\ begin {tikzpicture} [hoja de estilo ipe, escala=.7]\ draw [relleno = ¡blanco! ¡80! negro] (100, 528) — (196, 656) — (220, 656) — (124, 528) — ciclo;\ draw [fill=white! ¡80! negro] (208, 664) — (320, 712) — (320, 696) — (208, 648) — ciclo;\ begin {scope} [shift= {(321.91, 715.847)}, rotar=-9.1623]\ draw [fill=white! ¡90! negro] (0, 0) — (48, 12) — (96, 0) — (96, -4) — (20, -4) — (20, -20) — (96, -20) — (96, -24) — (48, -36) — (0, -24) — ciclo;\ draw [fill=rojo] (96, -12) círculo [radio = 1mm] nodo [derecha=2mm, rojo] {$\ vec {x y} = f (\ theta,\ phi,\ psi) $};\ end {scope}\ filldraw [filldraw [fill=white] (208, 656) circle [radius=16];\ filldraw [ fill=blanco] (320, 704) circle [radius=16];\ filldraw [fill=white] (112, 528) circle [radius=24];\ filldraw [blanco! ¡20! negro] (112, 528) círculo [radius=4] (208, 656) círculo [radius=4] (320, 704) círculo [radius=4];\ coordenada (c1) en (112, 528);\ coordenada (c2) en (208, 656);\ coordenada (c3) en (320, 704);\ coordenada (x1) en ($ (c1) + (2cm,0) $);\ coordenada (x3) a ($ (c3) + (2cm,0) $);\ draw (c1) — (x1);\ draw (c1) — ($ (c1)! ¡2cm! (c2) $);\ pic [dibujar, “$\ theta$”, ángulo radio = 1cm, ángulo excentricidad=.8] {angle=x1—c1—c2};\ draw (c2) — ($ (c2)! ¡2cm! (c1) $);\ dibujar (c2) — ($ (c2)! ¡2cm! (c3) $);\ pic [dibujar, “$\ phi$”, ángulo radio = 1cm, ángulo excentricidad=.8] {angle=c1—c2—c3};\ coordenada (x3p) en ($ (c3)! ¡2cm! -9.1623: (x3) $);\ dibujar (c3) — ($ (c3)! ¡2cm! (c2) $);\ draw (c3) — (x3p);\ pic [dibujar, “$\ psi$”, ángulo radio = 1cm, ángulo excentricidad=.8] {angle=c2—c3—x3p};\ end {tikzpicture}

Definir una transformación de la$f$ siguiente manera:$f(\theta,\phi,\psi)$ es la$(x,y)$ posición de la mano cuando las juntas se rotan en ángulos$\theta, \phi, \psi\text{,}$ respectivamente. La salida de$f$ le indica dónde estará la mano en el plano cuando las juntas se establecen en los ángulos de entrada dados.

Desafortunadamente, este tipo de función no proviene de una matriz, por lo que no se puede usar álgebra lineal para responder preguntas sobre esta función. De hecho, estas funciones son bastante complicadas; su estudio es objeto de cinemática inversa.

En este capítulo, nos ocuparemos de la relación entre matrices y transformaciones. En la Sección 3.1, consideraremos la ecuación$b = Ax$ como una función con variable independiente$x$ y variable dependiente$b\text{,}$ y dibujaremos imágenes en consecuencia. Pasamos algún tiempo estudiando transformaciones en abstracto, y haciendo preguntas sobre una transformación, como si es uno a uno y/o sobre (Sección 3.2). En la Sección 3.3 vamos a responder a la pregunta: “¿cuándo exactamente se puede expresar una transformación mediante una matriz?” A continuación se presenta la multiplicación matricial como un caso especial de composición de transformaciones (Sección 3.4). Esto lleva al estudio del álgebra matricial: es decir, en qué medida se puede hacer aritmética con matrices en lugar de números. Con esto en su lugar, aprendemos a resolver ecuaciones matriciales dividiendo por una matriz en la Sección 3.5.