3.1: Transformaciones matriciales
- Page ID
- 113106
- Aprende a ver una matriz geométricamente como una función.
- Aprende ejemplos de transformaciones matriciales: reflexión, dilatación, rotación, cizallamiento, proyección.
- Comprender el vocabulario que rodea las transformaciones: dominio, codominio, rango.
- Comprender el dominio, codominio y rango de una transformación matricial.
- Imágenes: transformaciones matriciales comunes.
- Palabras de vocabulario: transformación/función, dominio, codominio, rango, transformación de identidad, matriz transformación.
En esta sección aprendemos a entender las matrices geométricamente como funciones, o transformaciones. Discutimos brevemente las transformaciones en general, luego nos especializamos en transformaciones matriciales, que son transformaciones que provienen de matrices.
Matrices como funciones
Informalmente, una función es una regla que acepta entradas y produce salidas. Por ejemplo,\(f(x) = x^2\) es una función que acepta un número\(x\) como su entrada, y da salida al cuadrado de ese número:\(f(2) = 4\). En esta subsección, interpretamos las matrices como funciones.
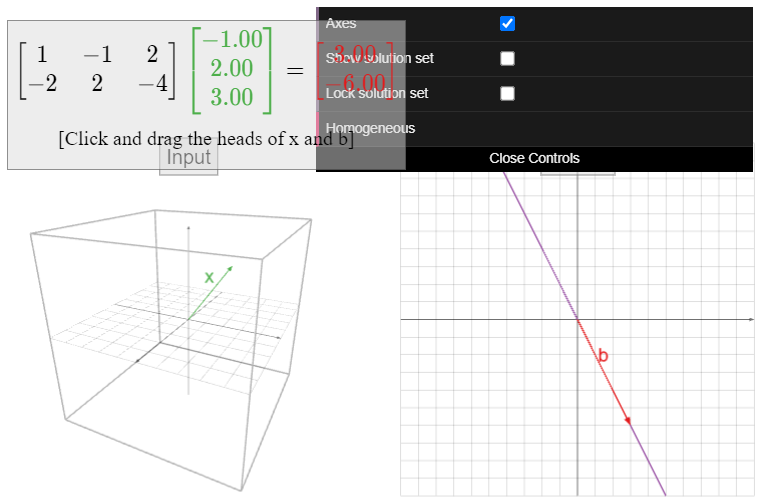
Dejar\(A\) ser una matriz con\(m\) filas y\(n\) columnas. Considera la ecuación matricial\(b=Ax\) (la escribimos de esta manera en lugar de recordarle\(Ax=b\) al lector la notación\(y=f(x)\)). Si variamos\(x\text{,}\) entonces también\(b\) variaremos; de esta manera, pensamos en\(A\) como una función con variable independiente\(x\) y variable dependiente\(b\).
- La variable independiente (la entrada) es\(x\text{,}\) que es un vector en\(\mathbb{R}^n \).
- La variable dependiente (la salida) es\(b\text{,}\) que es un vector en\(\mathbb{R}^m \).
El conjunto de todos los vectores de salida posibles son los vectores\(b\) tal que\(Ax=b\) tiene alguna solución; esto es lo mismo que el espacio de columna de\(A\) por Nota 2.3.6 en la Sección 2.3.
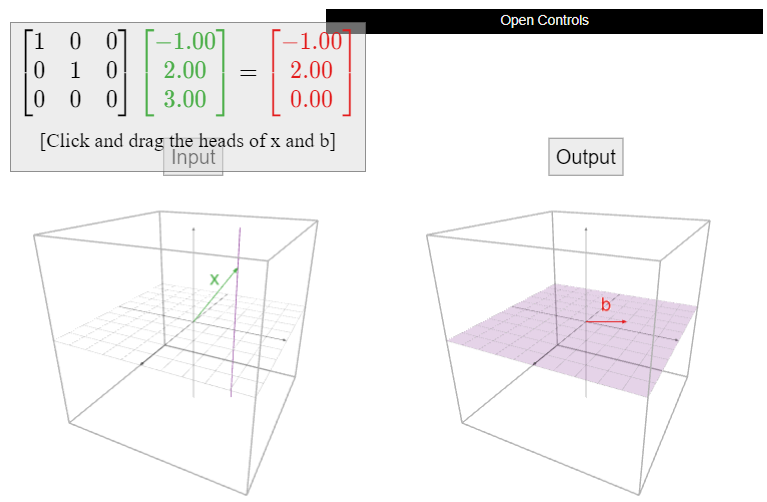
Figura\(\PageIndex{1}\)
Vamos
\[A=\left(\begin{array}{ccc}1&0&0\\0&1&0\\0&0&0\end{array}\right).\nonumber\]
Describir la función\(b=Ax\) geométricamente.
Solución
En la ecuación\(Ax=b\text{,}\) el vector de entrada\(x\) y el vector de salida\(b\) están ambos en\(\mathbb{R}^3 \). Primero multiplicamos\(A\) por un vector para ver qué hace:
\[A\left(\begin{array}{c}x\\y\\z\end{array}\right)=\left(\begin{array}{ccc}1&0&0\\0&1&0\\0&0&0\end{array}\right)\:\left(\begin{array}{c}x\\y\\z\end{array}\right)=\left(\begin{array}{c}x\\y\\0\end{array}\right).\nonumber\]
La multiplicación por\(A\) simplemente establece la\(z\) coordenada -igual a cero: se proyecta verticalmente sobre el\(xy\) plano.
Figura\(\PageIndex{4}\)
Vamos
\[A=\left(\begin{array}{cc}-1&0\\0&1\end{array}\right).\nonumber\]
Describir la función\(b=Ax\) geométricamente.
Solución
En la ecuación\(Ax=b\text{,}\) el vector de entrada\(x\) y el vector de salida\(b\) están ambos en\(\mathbb{R}^2 \). Primero multiplicamos\(A\) por un vector para ver qué hace:
\[A\left(\begin{array}{c}x\\y\end{array}\right)=\left(\begin{array}{cc}-1&0\\0&1\end{array}\right)\:\left(\begin{array}{c}x\\y\end{array}\right)=\left(\begin{array}{c}-x\\y\end{array}\right).\nonumber\]
La multiplicación por\(A\) niega la\(x\) coordenada: se refleja sobre el\(y\) eje.

Figura\(\PageIndex{6}\)

Vamos
\[A=\left(\begin{array}{cc}1.5&0\\0&1.5\end{array}\right).\nonumber\]
Describir la función\(b=Ax\) geométricamente.
Solución
En la ecuación\(Ax=b\text{,}\) el vector de entrada\(x\) y el vector de salida\(b\) están ambos en\(\mathbb{R}^2 \). Primero multiplicamos\(A\) por un vector para ver qué hace:
\[A\left(\begin{array}{c}x\\y\end{array}\right)=\left(\begin{array}{cc}1.5&0\\0&1.5\end{array}\right)\:\left(\begin{array}{c}x\\y\end{array}\right)=\left(\begin{array}{c}1.5x\\1.5y\end{array}\right)=1.5\left(\begin{array}{c}x\\y\end{array}\right).\nonumber\]
La multiplicación por\(A\) es lo mismo que la multiplicación escalar por\(1.5\text{:}\) ella escala o dilata el plano por un factor de\(1.5\).
Figura\(\PageIndex{8}\)

Vamos
\[A=\left(\begin{array}{cc}1&0\\0&1\end{array}\right).\nonumber\]
Describir la función\(b=Ax\) geométricamente.
Solución
En la ecuación\(Ax=b\text{,}\) el vector de entrada\(x\) y el vector de salida\(b\) están ambos en\(\mathbb{R}^2 \). Primero multiplicamos\(A\) por un vector para ver qué hace:
\[A\left(\begin{array}{c}x\\y\end{array}\right)=\left(\begin{array}{cc}1&0\\0&1\end{array}\right)\:\left(\begin{array}{c}x\\y\end{array}\right)=\left(\begin{array}{c}x\\y\end{array}\right).\nonumber\]
La multiplicación por\(A\) no cambia en absoluto el vector de entrada: es la transformación de identidad la que no hace nada.
Figura\(\PageIndex{10}\)

Vamos
\[A=\left(\begin{array}{cc}0&-1\\1&0\end{array}\right).\nonumber\]
Describir la función\(b=Ax\) geométricamente.
Solución
En la ecuación\(Ax=b\text{,}\) el vector de entrada\(x\) y el vector de salida\(b\) están ambos en\(\mathbb{R}^2 \). Primero multiplicamos\(A\) por un vector para ver qué hace:
\[A\left(\begin{array}{c}x\\y\end{array}\right)=\left(\begin{array}{cc}0&-1\\1&0\end{array}\right)\:\left(\begin{array}{c}x\\y\end{array}\right)=\left(\begin{array}{c}-y\\x\end{array}\right).\nonumber\]
Sustituimos algunos puntos de prueba para entender la geometría de la transformación:
Figura\(\PageIndex{12}\)
La multiplicación por\(A\) es rotación en sentido antihorario por\(90^\circ\).
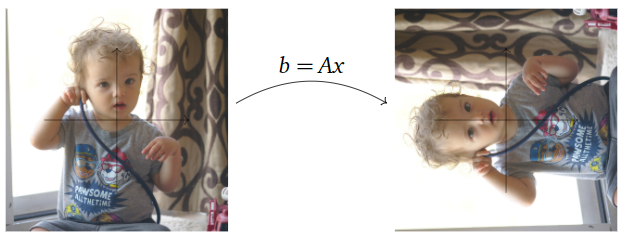
Figura\(\PageIndex{13}\)

Vamos
\[A=\left(\begin{array}{cc}1&1\\0&1\end{array}\right).\nonumber\]
Describir la función\(b=Ax\) geométricamente.
Solución
En la ecuación\(Ax=b\text{,}\) el vector de entrada\(x\) y el vector de salida\(b\) están ambos en\(\mathbb{R}^2 \). Primero multiplicamos\(A\) por un vector para ver qué hace:
\[A\left(\begin{array}{c}x\\y\end{array}\right)=\left(\begin{array}{cc}1&1\\0&1\end{array}\right)\:\left(\begin{array}{c}x\\y\end{array}\right)=\left(\begin{array}{c}x+y\\y\end{array}\right).\nonumber\]
La multiplicación por\(A\) agrega la\(y\) coordenada -a la\(x\) coordenada -; esto se denomina cizallamiento en la\(x\) dirección -dirección.
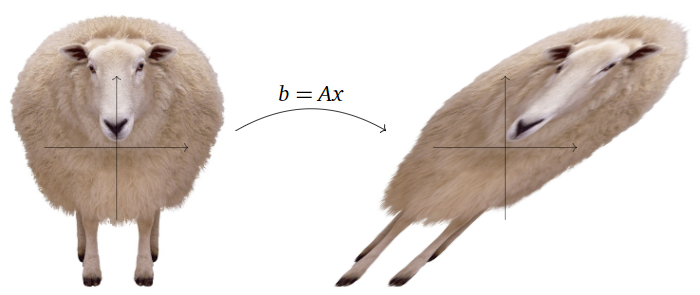
Figura\(\PageIndex{15}\)

Transformaciones
En este punto es conveniente fijar nuestras ideas y terminología respecto a las funciones, a las que llamaremos transformaciones en este libro. Esto nos permite sistematizar nuestra discusión sobre las matrices como funciones.
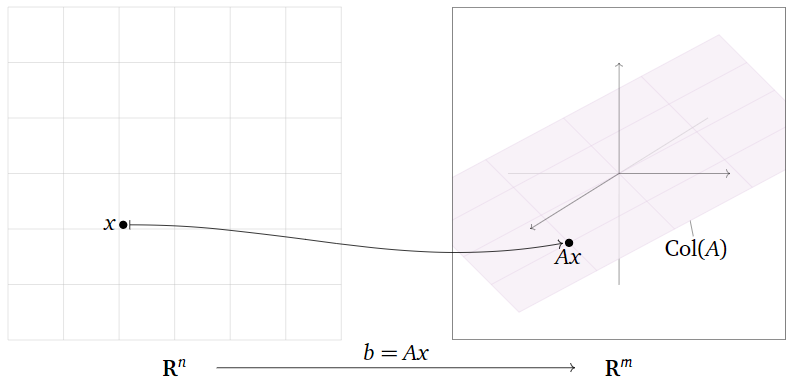
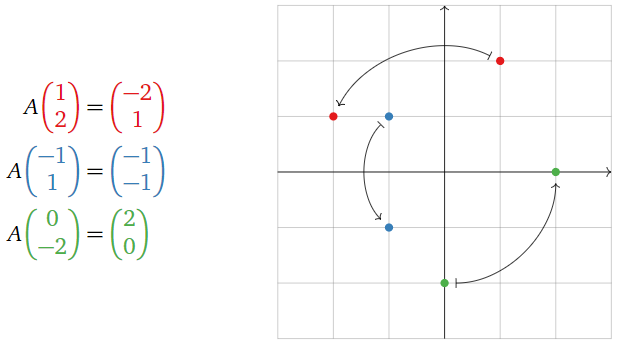
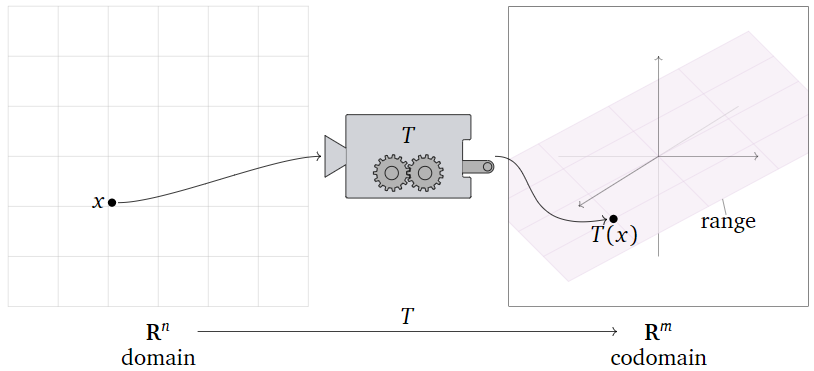
Una transformación de\(\mathbb{R}^n \) a\(\mathbb{R}^m \) es una regla\(T\) que asigna a cada vector\(x\) en\(\mathbb{R}^n \) un vector\(T(x)\) en\(\mathbb{R}^m \).
- \(\mathbb{R}^n \)se llama el dominio de\(T\).
- \(\mathbb{R}^m \)se llama el codominio de\(T\).
- Porque\(x\) en\(\mathbb{R}^n \text{,}\) el vector\(T(x)\) en\(\mathbb{R}^m \) es la imagen de\(x\) debajo\(T\).
- El conjunto de todas las imágenes\(\{T(x)\mid x\text{ in }\mathbb{R}^n \}\) es el rango de\(T\).
La notación\(T\colon\mathbb{R}^n \to \mathbb{R}^m \) significa “\(T\)es una transformación de\(\mathbb{R}^n \) a”\(\mathbb{R}^m \).
Puede ayudar pensar en ella\(T\) como una “máquina” que toma\(x\) como entrada, y te da\(T(x)\) como salida.
Figura\(\PageIndex{17}\)
Los puntos del dominio\(\mathbb{R}^n \) son las entradas de\(T\text{:}\) esto simplemente significa que tiene sentido evaluar\(T\) sobre vectores con\(n\) entradas, es decir, listas de\(n\) números. De igual manera, los puntos del codominio\(\mathbb{R}^m \) son las salidas de\(T\text{:}\) esto significa que el resultado de evaluar\(T\) es siempre un vector con\(m\) entradas.
El rango de\(T\) es el conjunto de todos los vectores en el codominio que realmente surgen como salidas de la función\(T\text{,}\) para alguna entrada. En otras palabras, el rango es todos los vectores\(b\) en el codominio tal que\(T(x)=b\) tiene una solución\(x\) en el dominio.
La mayoría de las funciones que puede haber visto anteriormente tienen dominio y codominio igual a\(\mathbb{R} = \mathbb{R}^1\). Por ejemplo,
\[\sin :\mathbb{R}\to\mathbb{R}\quad\sin(x)=\left(\begin{array}{l}\text{the length of the opposite} \\ \text{edge over the hypotenuse of} \\ \text{a right triangle with angle }x \\ \text{in radians}\end{array}\right).\nonumber\]
Observe que hemos definido\(\sin\) por una regla: una función se define especificando cuál es la salida de la función para cualquier entrada posible.
Usted puede estar acostumbrado a pensar en tales funciones en términos de sus gráficas:
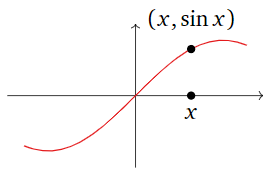
Figura\(\PageIndex{18}\)
En este caso, el eje horizontal es el dominio, y el eje vertical es el codominio. Esto es útil cuando el dominio y el codominio lo son\(\mathbb{R}\text{,}\) pero es difícil de hacer cuando, por ejemplo, el dominio es\(\mathbb{R}^2 \) y el codominio lo es\(\mathbb{R}^3 \). El gráfico de tal función es un subconjunto del\(\mathbb{R}^5\text{,}\) cual es difícil de visualizar. Por esta razón, rara vez vamos a graficar una transformación.
Tenga en cuenta que el rango de\(\sin\) es el intervalo\([-1,1]\text{:}\) este es el conjunto de todas las salidas posibles de la\(\sin\) función.
Aquí hay un ejemplo de una función de\(\mathbb{R}^2 \) a\(\mathbb{R}^3 \text{:}\)
\[f\left(\begin{array}{c}x\\y\end{array}\right)=\left(\begin{array}{c}x+y\\ \cos(y) \\y-x^{2}\end{array}\right).\nonumber\]
Las entradas de\(f\) cada una tienen dos entradas, y las salidas tienen tres entradas. En este caso, hemos definido\(f\) por una fórmula,\(f\) por lo que evaluamos sustituyendo valores por las variables:
\[f\left(\begin{array}{c}2\\3\end{array}\right)=\left(\begin{array}{c}2+3 \\ \cos(3) \\ 3-2^2\end{array}\right)=\left(\begin{array}{c}5\\ \cos(3)\\-1\end{array}\right).\nonumber\]
Aquí hay un ejemplo de una función de\(\mathbb{R}^3 \) a\(\mathbb{R}^3 \text{:}\)
\[f(v)=\left(\begin{array}{c}\text{the counterclockwise rotation} \\ \text{of }v\text{ by and angle of }42^\circ \text{ about} \\ \text{ the }z\text{-axis}\end{array}\right).\nonumber\]
Es decir,\(f\) toma un vector con tres entradas, luego lo gira; de ahí que la salida de\(f\) también tenga tres entradas. En este caso, hemos definido\(f\) por una regla geométrica.
La transformación de identidad \(\text{Id}_{\mathbb{R}^n }\colon\mathbb{R}^n \to\mathbb{R}^n \)es la transformación definida por la regla
\[ \text{Id}_{\mathbb{R}^n }(x) = x \qquad\text{for all $x$ in $\mathbb{R}^n $}. \nonumber \]
En otras palabras, la transformación de identidad no mueve su vector de entrada: la salida es la misma que la entrada. Su dominio y codominio son ambos\(\mathbb{R}^n \text{,}\) y su rango también\(\mathbb{R}^n \) lo es, ya que cada vector en\(\mathbb{R}^n \) es la salida de sí mismo.
La definición de transformación y su vocabulario asociado pueden parecer bastante abstractos, pero las transformaciones son extremadamente comunes en la vida real. Aquí un ejemplo de los campos de la robótica y la infografía.
Supongamos que está construyendo un brazo robot con tres articulaciones que pueden mover su mano alrededor de un plano, como en la siguiente imagen.
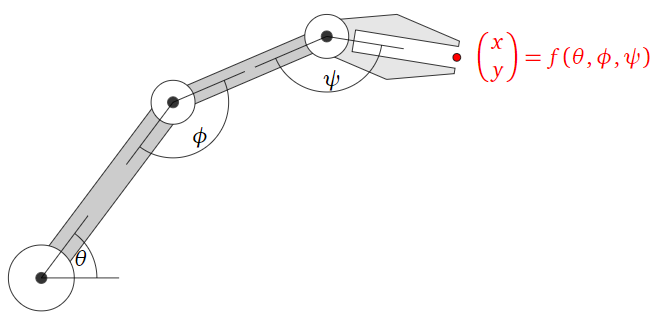
Figura\(\PageIndex{19}\)
Definir una transformación de la\(f\colon\mathbb{R}^3 \to\mathbb{R}^2 \) siguiente manera:\(f(\theta,\phi,\psi)\) es la\((x,y)\) posición de la mano cuando las juntas se rotan en ángulos\(\theta, \phi, \psi\text{,}\) respectivamente. Evaluar te\(f\) indica dónde estará la mano en el plano cuando las articulaciones se establecen en los ángulos dados.
Es relativamente sencillo encontrar una fórmula para\(f(\theta,\phi,\psi)\) usar alguna trigonometría básica. Si quieres que el robot vaya a buscar tu taza de café, sin embargo, tienes que encontrar los ángulos\(\theta,\phi,\psi\) que pondrán la mano en la posición de tu bebida. No es nada obvio cómo hacer esto, ¡y ni siquiera está claro si la respuesta es única! Puedes preguntarte: “¿qué posiciones sobre la mesa puede alcanzar mi brazo robot?” o “¿cuál es el rango de movimiento del brazo?” Esto es lo mismo que preguntar: “cuál es el rango de\(f\text{?}\)”
Desafortunadamente, este tipo de función no proviene de una matriz, por lo que no se puede usar álgebra lineal para responder a este tipo de preguntas. De hecho, estas funciones son bastante complicadas; su estudio es objeto de cinemática inversa.
Transformaciones matriciales
Ahora nos especializamos las nociones generales y vocabulario desde la Subsección Transformaciones anteriores hasta las funciones definidas por matrices que consideramos en la primera Subsección Matrices como Funciones.
\(A\)Déjese ser una\(m\times n\) matriz. La transformación matricial asociada a\(A\) es la transformación
\[ T\colon \mathbb{R}^n \to \mathbb{R}^m \quad\text{defined by}\quad T(x) = Ax. \nonumber \]
Esta es la transformación que lleva un vector\(x\)\(\mathbb{R}^n \) al vector\(Ax\) en\(\mathbb{R}^m \).
Si\(A\) tiene\(n\) columnas, entonces solo tiene sentido multiplicar\(A\) por vectores con\(n\) entradas. Es por ello que el dominio de\(T(x)=Ax\) es\(\mathbb{R}^n \). Si\(A\) tiene\(n\) filas, entonces\(Ax\) tiene\(m\) entradas para cualquier vector\(x\) en\(\mathbb{R}^n \text{;}\) esta es la razón por la que el codominio de\(T(x)=Ax\) es\(\mathbb{R}^m \).
La definición de una transformación matricial nos\(T\) dice cómo evaluar\(T\) en cualquier vector dado: multiplicamos el vector de entrada por una matriz. Por ejemplo, vamos
\[A=\left(\begin{array}{ccc}1&2&3\\4&5&6\end{array}\right)\nonumber\]
y dejar que\(T(x)=Ax\) sea la transformación matricial asociada. Entonces
\[T\left(\begin{array}{c}-1\\-2\\-3\end{array}\right)=A\left(\begin{array}{c}-1\\-2\\-3\end{array}\right)=\left(\begin{array}{ccc}1&2&3\\4&5&6\end{array}\right)\:\left(\begin{array}{c}-1\\-2\\-3\end{array}\right)=\left(\begin{array}{c}-14\\-32\end{array}\right).\nonumber\]
Supongamos que\(A\) tiene columnas\(v_1,v_2,\ldots,v_n\). Si multiplicamos\(A\) por un vector general\(x\text{,}\) obtenemos
\[Ax=\left(\begin{array}{cccc}|&|&\quad&| \\ v_1&v&2&\cdots &v_n \\ |&|&\quad &|\end{array}\right)\:\left(\begin{array}{c}x_1\\x_2\\ \vdots \\x_n\end{array}\right)=x_1v_1+x_2v_2+\cdots +x_nv_n.\nonumber\]
Esta es solo una combinación lineal general de\(v_1,v_2,\ldots,v_n\). Por lo tanto, las salidas de\(T(x) = Ax\) son exactamente las combinaciones lineales de las columnas\(A\text{:}\) del rango de\(T\) es el espacio de columna de\(A\). Véase la Nota 2.3.6 en la Sección 2.3.
Dejar\(A\) ser una\(m\times n\) matriz, y dejar\(T(x)=Ax\) ser la transformación matricial asociada.
- El dominio de\(T\) es\(\mathbb{R}^n \text{,}\) donde\(n\) está el número de columnas de\(A\).
- El codominio de\(T\) es\(\mathbb{R}^m \text{,}\) donde\(m\) está el número de filas de\(A\).
- El rango de\(T\) es el espacio de columna de\(A\).
Vamos
\[A=\left(\begin{array}{c}1&-1&2\\-2&2&4\end{array}\right),\nonumber\]
y definir\(T(x) = Ax\). El dominio de\(T\) es\(\mathbb{R}^3 \text{,}\) y el codominio es\(\mathbb{R}^2 \). El rango de\(T\) es el espacio de columna; dado que las tres columnas son colineales, el rango es una línea en\(\mathbb{R}^2 \).
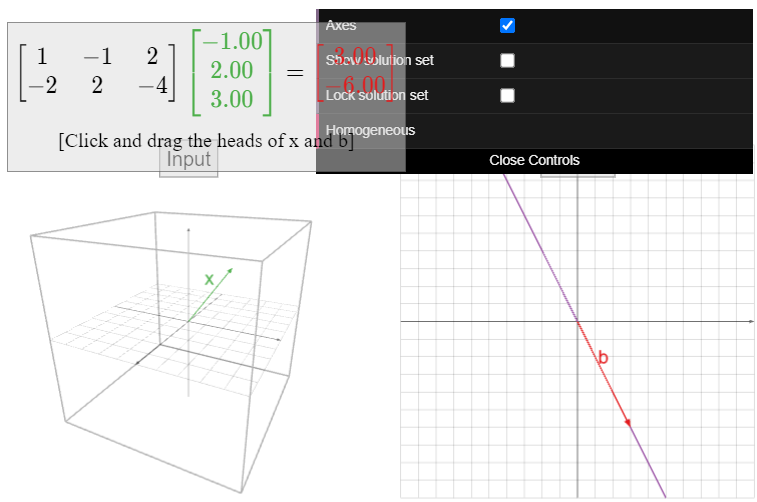
Vamos
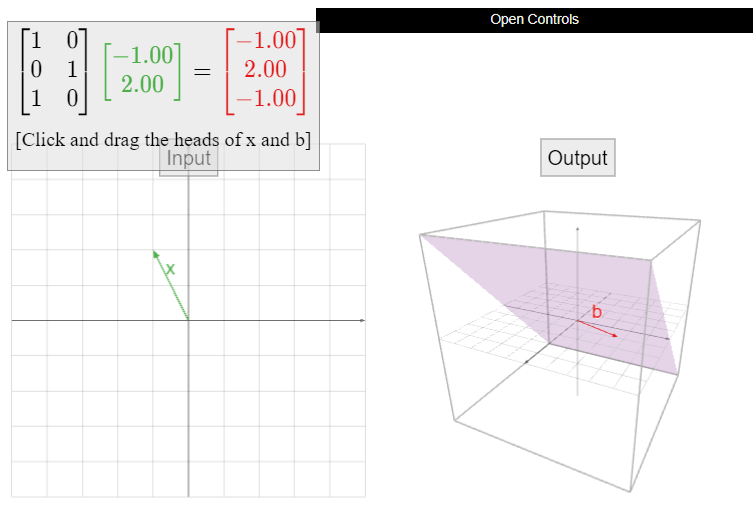
\[A=\left(\begin{array}{cc}1&0\\0&1\\1&0\end{array}\right),\nonumber\]
y definir\(T(x) = Ax\). El dominio de\(T\) es\(\mathbb{R}^2 \text{,}\) y el codominio es\(\mathbb{R}^3 \). El rango de\(T\) es el espacio de columna; ya que\(A\) tiene dos columnas que no son colineales, el rango es un plano en\(\mathbb{R}^3 \).
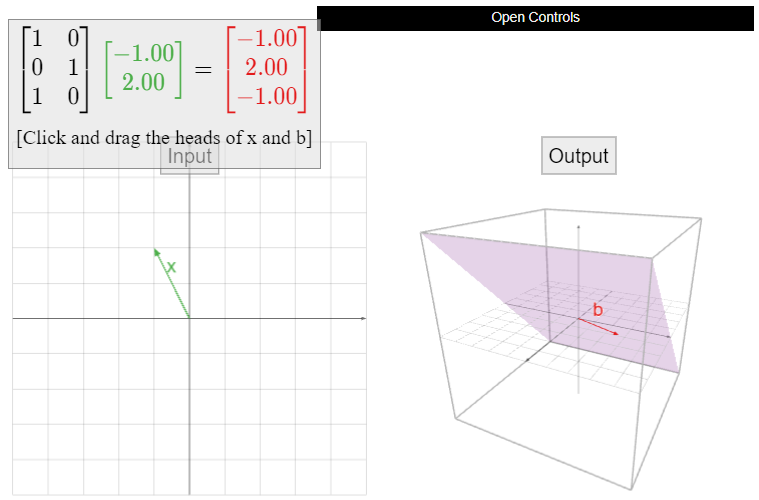
Vamos
\[A=\left(\begin{array}{ccc}1&0&0\\0&1&0\\0&0&0\end{array}\right),\nonumber\]
y vamos\(T(x) = Ax\). ¿Cuáles son el dominio, el codominio y el rango de\(T\text{?}\)
Solución
Geométricamente, la transformación\(T\) proyecta un vector directamente “hacia abajo” sobre el\(xy\) plano en\(\mathbb{R}^3 \).
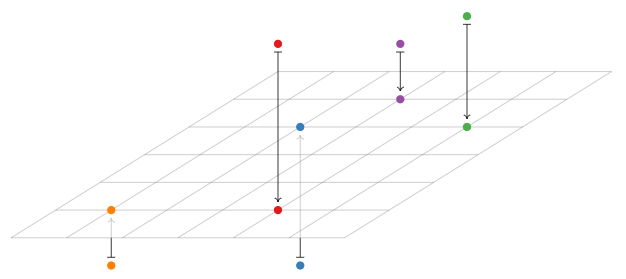
Figura\(\PageIndex{22}\)
Las entradas y salidas tienen tres entradas, por lo que el dominio y el codominio son ambos\(\mathbb{R}^3 \). Todas las salidas posibles se encuentran en el\(xy\) plano, y cada punto en el\(xy\) plano es una salida de\(T\) (consigo mismo como entrada), por lo que el rango de\(T\) es el\(xy\) plano.
Tenga cuidado de no confundir el codominio con el rango aquí. El rango es un plano, pero es un plano adentro\(\mathbb{R}^3 \), por lo que el codominio sigue siendo\(\mathbb{R}^3 \). Las salidas de\(T\) todas tienen tres entradas; la última entrada es simplemente siempre cero.
En el caso de una matriz\(n\times n\) cuadrada, el dominio y el codominio de\(T(x) = Ax\) son ambos\(\mathbb{R}^n \). En esta situación, se puede considerar\(T\) como operando sobre\(\mathbb{R}^n \text{:}\) él mueve los vectores alrededor en un mismo espacio.
En la primera Subsección Matrices como Funciones discutimos las transformaciones definidas por varias\(2\times 2\) matrices, a saber:
\ begin {align*}\ text {Reflection:} &\ qquad A=\ left (\ begin {array} {cc} -1&0\\ 0&1\ end {array}\ right)\\\ text {Dilatación:} &\ qquad A=\ left (\ begin {array} {cc} 1.5&0\\ 0&1.5\ end {array}\ right)\\ text {Identidad:} &\ qquad A=\ left (\ begin {array} {cc} 1&0\\ 0&1\ end {array}\ derecha)\\\ text {Rotación:} &\ qquad A=\ left (\ begin {array} {cc} 0&-1\\ 1&0\ end {array}\ right)\\\ text {Shear:} &\ qquad A=\ left (\ begin {array} {cc} 1&1\\ 0&1\ end {array}\ right). \ end {align*}
En cada caso, la transformación matricial asociada\(T(x)=Ax\) tiene dominio y codominio igual a\(\mathbb{R}^2 \). El rango también es\(\mathbb{R}^2 \text{,}\) como se puede ver geométricamente (¿cuál es la entrada para una salida dada?) , o utilizando el hecho de que las columnas de no\(A\) son colineales (por lo que forman una base para\(\mathbb{R}^2 \)).
Vamos
\[A=\left(\begin{array}{cc}1&1\\0&1\\1&1\end{array}\right),\nonumber\]
y dejar\(T(x)=Ax\text{,}\) que así\(T\colon\mathbb{R}^2 \to\mathbb{R}^3 \) sea una transformación matricial.
- Evaluar\(T(u)\) para\(u=\left(\begin{array}{c}3\\4\end{array}\right)\).
- Vamos
\[ b = \left(\begin{array}{c}7\\5\\7\end{array}\right). \nonumber \]
Encuentra un vector\(v\) en\(\mathbb{R}^2 \) tal que\(T(v)=b\). ¿Hay más de uno? - ¿Existe un vector\(w\) en\(\mathbb{R}^3 \) tal que haya más de uno\(v\) en\(\mathbb{R}^2 \) con\(T(v)=w\text{?}\)
- Encuentra un vector\(w\) en el\(\mathbb{R}^3 \) que no esté en el rango de\(T\).
Nota: todas las preguntas anteriores son intrínsecas a la transformación\(T\text{:}\) que tienen sentido para preguntar si\(T\) es o no una transformación matricial. Ver el siguiente Ejemplo\(\PageIndex{17}\). Como\(T\) es de hecho una transformación matricial, todas estas preguntas se traducirán en preguntas sobre la matriz correspondiente\(A\).
Solución
- Evaluamos\(T(u)\) sustituyendo la definición de\(T\) en términos de multiplicación matricial:
\[T\left(\begin{array}{c}3\\4\end{array}\right)=\left(\begin{array}{cc}1&1\\0&1\\1&1\end{array}\right)\:\left(\begin{array}{c}3\\4\end{array}\right)=\left(\begin{array}{c}7\\4\\7\end{array}\right).\nonumber\] - Queremos encontrar un vector\(v\) tal que\(b = T(v) = Av\). En otras palabras, queremos resolver la ecuación matricial\(Av = b\). Formamos una matriz aumentada y la fila reduce:
\[\left(\begin{array}{cc}1&1\\0&1\\1&1\end{array}\right)v=\left(\begin{array}{c}7\\5\\7\end{array}\right) \quad\xrightarrow{\text{augmented matrix}}\quad\left(\begin{array}{cc|c}1&1&7\\0&1&5\\1&1&7\end{array}\right) \quad\xrightarrow{\text{row reduce}}\quad\left(\begin{array}{cc|c}1&0&2\\0&1&5\\0&0&0\end{array}\right).\nonumber\]
Esto da\(x=2\) y\(y=5\text{,}\) para que haya un vector único
\[ v = \left(\begin{array}{c}2\\5\end{array}\right) \nonumber \]
tal que\(T(v) = b\). - Traducción: ¿hay algún vector\(w\) en\(\mathbb{R}^3 \) tal que el conjunto de soluciones de\(Av=w\) tenga más de un vector en él? El conjunto de soluciones de\(Ax=w\text{,}\) si no está vacío, es una traducción del conjunto de soluciones\(Av=b\) anterior, que tiene un vector en él. Véase la observación clave 2.4.3 en la Sección 2.4. De ello se deduce que el conjunto de soluciones de\(Av=w\) puede tener como máximo un vector.
- Traducción: encontrar un vector\(w\) tal que la ecuación matricial no\(Av=w\) sea consistente. Observe que si tomamos
\[ w = \left(\begin{array}{c}1\\2\\3\end{array}\right)\text{,} \nonumber \]
entonces la ecuación matricial\(Av=w\) se traduce en el sistema de ecuaciones
\[\left\{\begin{array}{rrrrl}x &+& y &=& 1\\ {}&{}& y &=& 2\\ x &+& y &=& 3,\end{array}\right.\nonumber\]
que es claramente inconsistente.
Definir una transformación\(T\colon\mathbb{R}^2 \to\mathbb{R}^3 \) por la fórmula
\[T\left(\begin{array}{c}x\\y\end{array}\right)=\left(\begin{array}{c}\ln(x) \\ \cos(y) \\ \ln(x)\end{array}\right).\nonumber\]
- Evaluar\(T(u)\) para\(u=\left(\begin{array}{c}1\\ \pi\end{array}\right)\).
- Vamos
\[ b = \left(\begin{array}{c}7\\1\\7\end{array}\right). \nonumber \]
Encuentra un vector\(v\) en\(\mathbb{R}^2 \) tal que\(T(v)=b\). ¿Hay más de uno? - ¿Existe un vector\(w\) en\(\mathbb{R}^3 \) tal que haya más de uno\(v\) en\(\mathbb{R}^2 \) con\(T(v)=w\text{?}\)
- Encuentra un vector\(w\) en el\(\mathbb{R}^3 \) que no esté en el rango de\(T\).
Nota: hicimos (casi) exactamente las mismas preguntas sobre una transformación matricial en el Ejemplo anterior\(\PageIndex{16}\). El objetivo de este ejemplo es ilustrar el hecho de que las preguntas tienen sentido para una transformación que no tiene esperanzas de provenir de una matriz. En este caso, estas preguntas no se traducen en preguntas sobre una matriz; tienen que ser respondidas de alguna otra manera.
Solución
- Evaluamos\(T(u)\) usando la fórmula definitoria:
\[T\left(\begin{array}{c}1\\ \pi\end{array}\right)=\left(\begin{array}{c} \ln(1) \\ \cos(\pi ) \\ \ln(1)\end{array}\right)=\left(\begin{array}{c}0\\-1\\0\end{array}\right).\nonumber\] - Tenemos
\[T\left(\begin{array}{c}e^7 \\ 2\pi n \\ e^7\end{array}\right)=\left(\begin{array}{c}\ln(e^7) \\ \cos (2\pi n) \\ \ln(e^7)\end{array}\right)=\left(\begin{array}{c}7\\1\\7\end{array}\right)\nonumber\]
para cualquier número entero\(n\). De ahí que haya infinitamente muchos de esos vectores. - El vector\(b\) de la parte anterior es un ejemplo de dicho vector.
- Dado que siempre\(\cos(y)\) está entre\(-1\) y\(1\text{,}\) el vector no
\[ w = \left(\begin{array}{c}0\\2\\0\end{array}\right) \nonumber \]
está en el rango de\(T\).