Search

Text Color

Margin Size

Font Type

Enable Dyslexic Font

4.1: Ejemplo de sistema lineal

Última actualización

30 oct 2022
Guardar como PDF
- 4.0: Introducción
- 4.2: Revisión de tareas previas a clase

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$ $\newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$ $\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$ $\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$ $\newcommand{\AA}{\unicode[.8,0]{x212B}}$

$\newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$\newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$\newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vectorC}[1]{\textbf{#1}}$

$\newcommand{\vectorD}[1]{\overrightarrow{#1}}$

$\newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}}$

$\newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}}$

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\avec}{\mathbf a}$

$\newcommand{\bvec}{\mathbf b}$

$\newcommand{\cvec}{\mathbf c}$

$\newcommand{\dvec}{\mathbf d}$

$\newcommand{\dtil}{\widetilde{\mathbf d}}$

$\newcommand{\evec}{\mathbf e}$

$\newcommand{\fvec}{\mathbf f}$

$\newcommand{\nvec}{\mathbf n}$

$\newcommand{\pvec}{\mathbf p}$

$\newcommand{\qvec}{\mathbf q}$

$\newcommand{\svec}{\mathbf s}$

$\newcommand{\tvec}{\mathbf t}$

$\newcommand{\uvec}{\mathbf u}$

$\newcommand{\vvec}{\mathbf v}$

$\newcommand{\wvec}{\mathbf w}$

$\newcommand{\xvec}{\mathbf x}$

$\newcommand{\yvec}{\mathbf y}$

$\newcommand{\zvec}{\mathbf z}$

$\newcommand{\rvec}{\mathbf r}$

$\newcommand{\mvec}{\mathbf m}$

$\newcommand{\zerovec}{\mathbf 0}$

$\newcommand{\onevec}{\mathbf 1}$

$\newcommand{\real}{\mathbb R}$

$\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$

$\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$

$\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$

$\newcommand{\laspan}[1]{\text{Span}\{#1\}}$

$\newcommand{\bcal}{\cal B}$

$\newcommand{\ccal}{\cal C}$

$\newcommand{\scal}{\cal S}$

$\newcommand{\wcal}{\cal W}$

$\newcommand{\ecal}{\cal E}$

$\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$

$\newcommand{\gray}[1]{\color{gray}{#1}}$

$\newcommand{\lgray}[1]{\color{lightgray}{#1}}$

$\newcommand{\rank}{\operatorname{rank}}$

$\newcommand{\row}{\text{Row}}$

$\newcommand{\col}{\text{Col}}$

$\renewcommand{\row}{\text{Row}}$

$\newcommand{\nul}{\text{Nul}}$

$\newcommand{\var}{\text{Var}}$

$\newcommand{\corr}{\text{corr}}$

$\newcommand{\len}[1]{\left|#1\right|}$

$\newcommand{\bbar}{\overline{\bvec}}$

$\newcommand{\bhat}{\widehat{\bvec}}$

$\newcommand{\bperp}{\bvec^\perp}$

$\newcommand{\xhat}{\widehat{\xvec}}$

$\newcommand{\vhat}{\widehat{\vvec}}$

$\newcommand{\uhat}{\widehat{\uvec}}$

$\newcommand{\what}{\widehat{\wvec}}$

$\newcommand{\Sighat}{\widehat{\Sigma}}$

$\newcommand{\lt}{<}$

$\newcommand{\gt}{>}$

$\newcommand{\amp}{&}$

$\definecolor{fillinmathshade}{gray}{0.9}$

Supongamos que tenemos tres objetos en una viga balanceada. También supongamos que sabemos que uno tiene una masa de 2 kg, y queremos encontrar las dos masas desconocidas. La experimentación con una barra medidora (supongamos que no tiene peso) produce estas dos balanzas. (diagrama no a escala)

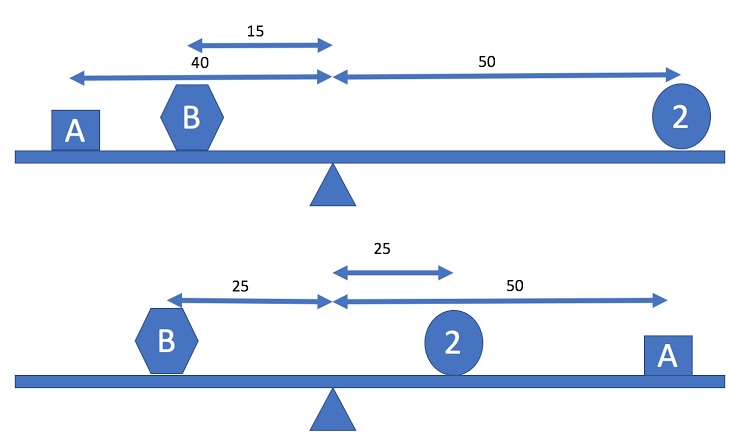
Figura $\PageIndex{1}$ : Imagen que muestra dos haces balanceados, cada uno con tres pesos. En la viga superior se desconoce el peso A es una distancia de 40 a la izquierda del fulcro, el peso desconocido B es una distancia de 15 a la izquierda del fulcro y un peso de 2 es 50 a la derecha del fulcro. En la viga inferior se encuentran los mismos pesos desconocidos. El peso A es ahora una distancia de 50 a la derecha del fulcro, el peso B es una distancia de 25 a la izquierda del fulcro y el peso de 2 es una distancia de 25 a la derecha del fulcro.

Para que las masas se equilibren debemos tener la suma de los momentos a la izquierda igual a la suma de los momentos de la derecha, donde el momento de un objeto es su masa multiplicada por su distancia del punto de equilibrio. Eso da un sistema de dos ecuaciones:

$40A + 15B = 50 \times 2 \nonumber$

$25B = 25 \times 2 + 50A \nonumber$

Hacer esto

Encuentre una solución para los sistemas de ecuaciones anteriores y coloque su solución en la siguiente celda. Asegúrese de eliminar primero el texto instructivo en la celda.

If you have already signed in, please refresh the page.

# Put your answer to the above question here

# Put your answer to the above question here

Hacer esto

Usando Python como calculadora, verifica que la solución que has encontrado es correcta.

If you have already signed in, please refresh the page.

# Put your answer to the above question here

# Put your answer to the above question here

Hacer esto

Ahora consideremos un sistema donde tenemos tres masas desconocidas en lugar de dos. La experimentación con una varilla medidora produce los dos estados equilibrados que se muestran a continuación (diagrama no a escala). Escribe las ecuaciones para este sistema.

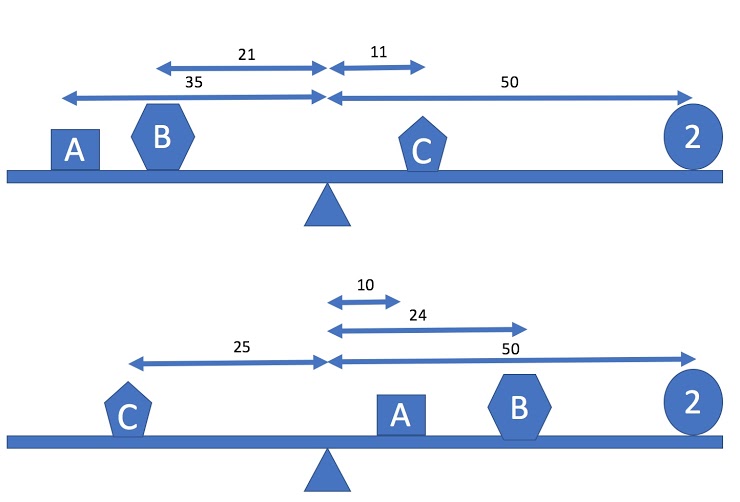
Figura $\PageIndex{2}$ : Imagen que muestra dos haces balanceados, cada uno con cuatro pesos. En la viga superior se desconoce el peso A que es una distancia de 35 a la izquierda del fulcro, el peso desconocido B es una distancia de 21 a la izquierda del fulcro, el peso desconocido C es una distancia de 11 a la derecha del fulcro y un peso de 2 es 50 a la derecha del fulcro. En la viga inferior se encuentran los mismos pesos desconocidos. El peso A se encuentra ahora a una distancia de 10 a la derecha del fulcro, el peso B es una distancia de 24 a la derecha del fulcro, el peso C es una distancia de 25 a la izquierda del fulcro y el peso de 2 sigue a una distancia de 50 a la derecha del fulcro.

Hacer esto

Encuentre una solución al segundo conjunto de ecuaciones y reporte la masa de los objetos A, B y C.

If you have already signed in, please refresh the page.

# Put your answer to the above question here

# Put your answer to the above question here

Hacer esto

Usando Python como calculadora, verifica que la solución que has encontrado es correcta.

If you have already signed in, please refresh the page.

# Put your answer to the above question here

# Put your answer to the above question here

Hacer esto

Hacer esto

Hacer esto

Hacer esto

Hacer esto

Support Center

How can we help?