2.4: Soluciones vectoriales para sistemas lineales

Objetivos de aprendizaje

• T/F: La ecuación\(A\vec{x}=\vec{b}\) es sólo otra forma de escribir un sistema de ecuaciones lineales.
• T/F: Al resolver\(A\vec{x}=\vec{0}\), si hay 3 variables libres, entonces la solución se “separará” en 3 vectores.
• T/F: Un sistema homogéneo de ecuaciones lineales es aquel en el que todos los coeficientes son 0.
• Que la ecuación\(A\vec{x}=\vec{b}\) tenga o no una solución depende de una propiedad intrínseca de _____.

El primer capítulo de este texto se dedicó a encontrar soluciones a sistemas de ecuaciones lineales. Hemos pasado las dos primeras secciones de este capítulo aprendiendo operaciones que se pueden realizar con matrices. Uno puede haberse preguntado “¿Las ideas del primer capítulo están relacionadas con lo que hemos estado haciendo recientemente?” La respuesta es sí, estas ideas están relacionadas. Esta sección comienza a mostrar esa relación.

A menudo hemos escuchado la experiencia previa en álgebra para ayudar a comprender los conceptos de álgebra matricial. Lo hacemos de nuevo aquí. Considera la ecuación\(ax=b\), dónde\(a=3\) y\(b=6\). Si le pidiéramos a uno que “\(x\)resolviera”, ¿qué le estaríamos preguntando exactamente? Nos gustaría encontrar un número, al que llamamos\(x\), donde los\(a\) tiempos\(x\) dan\(b\); en este caso, es un número, cuando se multiplica por 3, devuelve 6.

Ahora consideramos expresiones de álgebra matricial. Eventualmente consideraremos resolver ecuaciones como\(AX=B\), donde sabemos cuáles son las matrices\(A\) y\(B\) son y queremos encontrar la matriz\(X\). Por ahora, solo consideraremos ecuaciones del tipo\(A\vec{x}=\vec{b}\), donde conocemos la matriz\(A\) y el vector\(\vec{b}\). Vamos a querer encontrar qué vector\(\vec{x}\) satisface esta ecuación; queremos “resolver para”\(\vec{x}\).

Para ayudar a entender lo que esto está pidiendo, consideraremos un ejemplo. Let

\[A=\left[\begin{array}{ccc}{1}&{1}&{1}\\{1}&{-1}&{2}\\{2}&{0}&{1}\end{array}\right],\quad\vec{b}=\left[\begin{array}{c}{2}\\{-3}\\{1}\end{array}\right]\quad\text{and}\quad\vec{x}=\left[\begin{array}{c}{x_{1}}\\{x_{2}}\\{x_{3}}\end{array}\right]. \nonumber \]

(No sabemos qué\(\vec{x}\) es, así que tenemos que representar sus entradas con las variables\(x_1\),\(x_2\) y\(x_3\).) Vamos a “resolver por”\(\vec{x}\), dada la ecuación\(A\vec{x}=\vec{b}\).

Podemos multiplicar el lado izquierdo de esta ecuación. Nos encontramos con que

\[A\vec{x}=\left[\begin{array}{c}{x_{1}+x_{2}+x_{3}}\\{x_{1}-x_{2}+2x_{3}}\\{2x_{1}+x_{3}}\end{array}\right]. \nonumber \]

Asegúrese de señalar que el producto es solo un vector; tiene solo una columna.

Ya que\(A\vec{x}\) es igual a\(\vec{b}\), tenemos

\[\left[\begin{array}{c}{x_{1}+x_{2}+x_{3}}\\{x_{1}-x_{2}+2x_{3}}\\{2x_{1}+x_{3}}\end{array}\right]=\left[\begin{array}{c}{2}\\{-3}\\{1}\end{array}\right]. \nonumber \]

Sabiendo que dos vectores son iguales solo cuando sus entradas correspondientes son iguales, sabemos\[\begin{align}\begin{aligned} x_1+x_2+x_3&=2\\x_1-x_2+2x_3&=-3\\2x_1+x_3&=1.\end{aligned}\end{align} \nonumber \]

Esto debería parecer familiar; ¡es un sistema de ecuaciones lineales! Dada la ecuación matriz-vector\(A\vec{x}=\vec{b}\), podemos reconocer\(A\) como la matriz de coeficientes de un sistema lineal y\(\vec{b}\) como el vector de las constantes del sistema lineal. Para resolver una ecuación matriz-vector (y el sistema lineal correspondiente), simplemente aumentamos la matriz\(A\) con el vector\(\vec{b}\), colocamos esta matriz en forma de escalón de fila reducida e interpretamos los resultados.

Convertimos el sistema lineal anterior en una matriz aumentada y encontramos la forma de escalón de fila reducida:

\[\left[\begin{array}{cccc}{1}&{1}&{1}&{2}\\{1}&{-1}&{2}&{-3}\\{2}&{0}&{1}&{1}\end{array}\right]\quad\vec{\text{rref}}\quad\left[\begin{array}{cccc}{1}&{0}&{0}&{1}\\{0}&{1}&{0}&{2}\\{0}&{0}&{1}&{-1}\end{array}\right]. \nonumber \]

Esto nos dice que\(x_1=1\),\(x_2=2\) y\(x_3 = -1\), entonces

\[\vec{x}=\left[\begin{array}{c}{1}\\{2}\\{-1}\end{array}\right]. \nonumber \]

Deberíamos revisar nuestro trabajo; multiplicar\(A\vec{x}\) y verificar que efectivamente obtenemos\(\vec{b}\):

\[\left[\begin{array}{ccc}{1}&{1}&{1}\\{1}&{-1}&{2}\\{2}&{0}&{1}\end{array}\right]\:\left[\begin{array}{c}{1}\\{2}\\{-1}\end{array}\right]\quad\text{does equal}\quad\left[\begin{array}{c}{2}\\{-3}\\{1}\end{array}\right]. \nonumber \]

Deberíamos practicar.

Ejemplo\(\PageIndex{1}\)

Resuelve la ecuación\(A\vec{x}=\vec{b}\) para\(\vec{x}\) dónde

\[A=\left[\begin{array}{ccc}{1}&{2}&{3}\\{-1}&{2}&{1}\\{1}&{1}&{0}\end{array}\right]\quad\text{and}\quad\left[\begin{array}{c}{5}\\{-1}\\{2}\end{array}\right]. \nonumber \]

Solución

La solución es bastante sencilla, a pesar de que antes hicimos mucho trabajo para encontrar la respuesta. Formar la matriz aumentada\([A\:\:\vec{b}]\) e interpretar su forma de escalón de fila reducida.

\[\left[\begin{array}{cccc}{1}&{2}&{3}&{5}\\{-1}&{2}&{1}&{-1}\\{1}&{1}&{0}&{2}\end{array}\right]\quad\vec{\text{rref}}\quad\left[\begin{array}{cccc}{1}&{0}&{0}&{2}\\{0}&{1}&{0}&{0}\\{0}&{0}&{1}&{1}\end{array}\right] \nonumber \]

En secciones anteriores estuvimos bien afirmando que el resultado como\[x_1=2, \quad x_2=0,\quad x_3=1, \nonumber \] pero nos pidieron que encontráramos\(\vec{x}\); por lo tanto, declaramos la solución como\[\vec{x}=\left[\begin{array}{c}{2}\\{0}\\{1}\end{array}\right]. \nonumber \]

Esto probablemente parece todo bien y bien. Si bien pedirle a uno que resuelva la ecuación\(A\vec{x}=\vec{b}\)\(\vec{x}\) parece un problema nuevo, en realidad es solo pedir que resolvamos un sistema de ecuaciones lineales. Nuestras variables\(x_1\), etc., aparecen no individualmente sino como las entradas de nuestro vector\(\vec{x}\). Simplemente estamos escribiendo un viejo problema de una manera nueva.

En línea con esta nueva forma de escribir el problema, tenemos una nueva forma de escribir la solución. En lugar de enumerar, individualmente, los valores de las incógnitas, simplemente los enumeramos como los elementos de nuestro vector\(\vec{x}\).

Estas son ideas importantes, por lo que declaramos una vez más el principio básico: resolver la ecuación\(A\vec{x}=\vec{b}\) para\(\vec{x}\) es lo mismo que resolver un sistema lineal de ecuaciones. Equivalentemente, cualquier sistema de ecuaciones lineales se puede escribir en la forma\(A\vec{x}=\vec{b}\) para alguna matriz\(A\) y vector\(\vec{b}\).

Como estas ideas son equivalentes, nos referiremos\(A\vec{x}=\vec{b}\) tanto como una ecuación matriz-vector como como un sistema de ecuaciones lineales: son lo mismo.

Hemos visto dos ejemplos que ilustran esta idea hasta ahora, y en ambos casos el sistema lineal tenía exactamente una solución. Sabemos por el Teorema 1.4.1 que cualquier sistema lineal tiene ya sea una solución, soluciones infinitas, o ninguna solución. Entonces, ¿cómo funciona nuestro nuevo método de escribir una solución con infinitas soluciones y sin soluciones?

Ciertamente, si no\(A\vec{x}=\vec{b}\) tiene solución, simplemente decimos que el sistema lineal no tiene solución. No hay nada especial que escribir. Entonces la única otra opción a considerar es el caso donde tenemos infinitas soluciones. Aprenderemos a manejar estas situaciones a través de ejemplos.

Ejemplo\(\PageIndex{2}\)

Resolver el sistema\(A\vec{x}=\vec{0}\) lineal\(\vec{x}\) y escribir la solución en forma vectorial, donde

\[A=\left[\begin{array}{cc}{1}&{2}\\{2}&{4}\end{array}\right]\quad\text{and}\quad\vec{0}=\left[\begin{array}{c}{0}\\{0}\end{array}\right]. \nonumber \]

Solución

Nota

Realmente no necesitábamos precisar eso\[\vec{0}=\left[\begin{array}{c}{0}\\{0}\end{array}\right], \nonumber \] pero lo hicimos solo para eliminar cualquier incertidumbre.

Para resolver este sistema, poner la matriz aumentada en forma de escalón de fila reducida, lo que hacemos a continuación.

\[\left[\begin{array}{ccc}{1}&{2}&{0}\\{2}&{4}&{0}\end{array}\right]\quad\vec{\text{rref}}\quad\left[\begin{array}{ccc}{1}&{2}&{0}\\{0}&{0}&{0}\end{array}\right] \nonumber \]

Interpretamos la forma de escalón de fila reducida de esta matriz para escribir la solución como

\[\begin{align}\begin{aligned} x_1 &= -2x_2\\x_2 &\text{ is free.}\end{aligned}\end{align} \nonumber \]

No hemos terminado; necesitamos escribir la solución en forma de vector, ya que nuestra solución es el vector\(\vec{x}\). Recordemos que

\[\vec{x}=\left[\begin{array}{c}{x_{1}}\\{x_{2}}\end{array}\right]. \nonumber \]

Desde arriba lo sabemos\(x_1 = -2x_2\), así que sustituimos el\(x_1\) in\(\vec{x}\) por\(-2x_2\). Esto le da a nuestra solución como

\[\vec{x}=\left[\begin{array}{c}{-2x_{2}}\\{x_{2}}\end{array}\right]. \nonumber \]

Ahora sacamos el\(x_2\) fuera del vector (es solo un escalar) y escribimos\(\vec{x}\) como

\[\vec{x}=x_{2}\left[\begin{array}{c}{-2}\\{1}\end{array}\right]. \nonumber \]

Por razones que quedarán más claras más adelante, establecer

\[\vec{v}=\left[\begin{array}{c}{-2}\\{1}\end{array}\right]. \nonumber \]

Por lo tanto, nuestra solución puede escribirse como

\[\vec{x}=x_{2}\vec{v}. \nonumber \]

Recordemos que como nuestro sistema era consistente y tenía una variable libre, tenemos infinitas soluciones. Esta forma de la solución resalta este hecho; elija cualquier valor para\(x_2\) y obtenemos una solución diferente.

Por ejemplo, configurando\(x_2 = -1\)\(0\), y\(5\), obtenemos las soluciones

\[\vec{x}=\left[\begin{array}{c}{2}\\{-1}\end{array}\right],\quad\left[\begin{array}{c}{0}\\{0}\end{array}\right],\quad\text{and}\quad\left[\begin{array}{c}{-10}\\{5}\end{array}\right], \nonumber \]

respectivamente.

Deberíamos revisar nuestro trabajo; multiplicar cada uno de los vectores anteriores por\(A\) para ver si efectivamente conseguimos\(\vec{0}\).

Oficialmente hemos resuelto este problema; hemos encontrado la solución\(A\vec{x}=\vec{0}\) y la hemos escrito correctamente. Una última cosa que haremos aquí es graficar la solución, utilizando nuestras habilidades aprendidas en la sección anterior.

Nuestra solución es

\[\vec{x}=x_{2}\left[\begin{array}{c}{-2}\\{1}\end{array}\right]. \nonumber \]

Esto significa que cualquier multiplicación escalar del vector\(\vec{v}=\left[\begin{array}{c}{-2}\\{1}\end{array}\right]\) es una solución; sabemos bosquejar los múltiplos escalares de\(\vec{v}\). Esto se hace en la Figura\(\PageIndex{1}\).

Figura\(\PageIndex{1}\): La solución, como línea, a\(A\vec{x}=\vec{0}\) en Ejemplo\(\PageIndex{2}\).

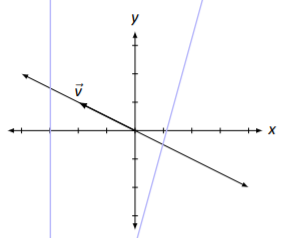
Aquí\(\vec{v}\) se dibuja el vector así como la línea que pasa por el origen en la dirección de\(\vec{v}\). Cualquier vector a lo largo de esta línea es una solución. Entonces en algún sentido, podemos decir que la solución a\(A\vec{x}=\vec{0}\) es una línea.

Practicemos esto de nuevo.

Ejemplo\(\PageIndex{3}\)

Resuelve el sistema lineal\(A\vec{x}=\vec{0}\) y escribe la solución en forma vectorial, donde

\[A=\left[\begin{array}{cc}{2}&{-3}\\{-2}&{3}\end{array}\right]. \nonumber \]

Solución

Nuevamente, para resolver este problema, formamos la matriz aumentada adecuada y la ponemos en forma de escalón de fila reducida, lo que hacemos a continuación.

\[\left[\begin{array}{ccc}{2}&{-3}&{0}\\{-2}&{3}&{0}\end{array}\right]\quad\vec{\text{rref}}\quad\left[\begin{array}{ccc}{1}&{-3/2}&{0}\\{0}&{0}&{0}\end{array}\right] \nonumber \]

Interpretamos la forma de escalón de fila reducida de esta matriz para encontrar que\[\begin{align}\begin{aligned} x_1 &= 3/2x_2 \\ x_2 &\text{ is free.} \end{aligned}\end{align} \nonumber \]

Como antes,

\[\vec{x}=\left[\begin{array}{c}{x_{1}}\\{x_{2}}\end{array}\right]. \nonumber \]

Ya que\(x_1 = 3/2x_2\),\(x_1\) reemplazamos\(\vec{x}\) con\(3/2x_2\):

\[\vec{x}=\left[\begin{array}{c}{3/2x_{2}}\\{x_{2}}\end{array}\right]. \nonumber \]

Ahora sacamos el\(x_2\) y escribimos la solución como

\[\vec{x}=x_{2}\left[\begin{array}{c}{3/2}\\{1}\end{array}\right]. \nonumber \]

Como antes, vamos a establecer

\[\vec{v}=\left[\begin{array}{c}{3/2}\\{1}\end{array}\right] \nonumber \]

para que podamos escribir nuestra solución como

\[\vec{x}=x_{2}\vec{v}. \nonumber \]

Nuevamente, tenemos infinitas soluciones; cualquier elección de nos\(x_2\) da una de estas soluciones. Por ejemplo, el picking\(x_2=2\) da la solución

\[\vec{x}=\left[\begin{array}{c}{3}\\{2}\end{array}\right]. \nonumber \]

(Esta es una solución particularmente agradable, ya que no hay fracciones\(\ldots\))

Al igual que en el ejemplo anterior, nuestras soluciones son múltiplos de un vector, y de ahí podemos graficar esto, como se hace en la Figura\(\PageIndex{2}\).

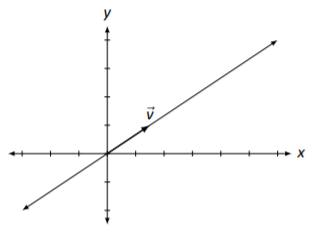
Figura\(\PageIndex{2}\): La solución, como línea, a\(A\vec{x}=\vec{0}\) en Ejemplo\(\PageIndex{3}\).

Practicemos un poco más; esta vez, no vamos a resolver un sistema de la forma\(A\vec{x}=\vec{0}\)\(A\vec{x}=\vec{b}\), sino para algún vector\(\vec{b}\).

Ejemplo\(\PageIndex{4}\)

Resolver el sistema lineal\(A\vec{x}=\vec{b}\), donde

\[A=\left[\begin{array}{cc}{1}&{2}\\{2}&{4}\end{array}\right]\quad\text{and}\quad\vec{b}=\left[\begin{array}{c}{3}\\{6}\end{array}\right]. \nonumber \]

Solución

Nota

Esta es la misma matriz\(A\) que usamos en Ejemplo\(\PageIndex{2}\). Esto será importante más adelante.

Nuestra metodología es la misma que antes; formamos la matriz aumentada y la ponemos en forma de escalón de fila reducida.

\[\left[\begin{array}{ccc}{1}&{2}&{3}\\{4}&{5}&{6}\end{array}\right]\quad\vec{\text{rref}}\quad\left[\begin{array}{ccc}{1}&{2}&{3}\\{0}&{0}&{0}\end{array}\right] \nonumber \]

Interpretando esta forma de escalón de fila reducida, encontramos que\[\begin{align}\begin{aligned} x_1 &= 3-2x_2\\ x_2 &\text{ is free.} \end{aligned}\end{align} \nonumber \] De nuevo,

\[\vec{x}=\left[\begin{array}{c}{x_{1}}\\{x_{2}}\end{array}\right], \nonumber \]

y reemplazamos\(x_1\) con\(3-2x_2\), dando

\[\vec{x}=\left[\begin{array}{c}{3-2x_{2}}\\{x_{2}}\end{array}\right]. \nonumber \]

Esta solución es diferente a lo que hemos visto en los dos últimos ejemplos; no podemos simplemente sacar una\(x_2\) ya que hay un 3 en la primera entrada. Usando las propiedades de la adición de matriz, podemos “separar” este vector y escribirlo como la suma de dos vectores: uno que contiene solo constantes, y otro que contiene solo “\(x_2\)cosas”. Esto lo hacemos a continuación.

\[\begin{align}\begin{aligned}\vec{x}&=\left[\begin{array}{c}{3-2x_{2}}\\{x_{2}}\end{array}\right] \\ &=\left[\begin{array}{c}{3}\\{0}\end{array}\right]+\left[\begin{array}{c}{-2x_{2}}\\{x_{2}}\end{array}\right] \\ &=\left[\begin{array}{c}{3}\\{0}\end{array}\right]+x_{2}\left[\begin{array}{c}{-2}\\{1}\end{array}\right].\end{aligned}\end{align} \nonumber \]

Una vez más, vamos a dar nombres a los diferentes vectores componentes de esta solución (nos estamos acercando a la explicación de por qué estamos haciendo esto). Let

\[\vec{x_{p}}=\left[\begin{array}{c}{3}\\{0}\end{array}\right]\quad\text{and}\quad\vec{v}=\left[\begin{array}{c}{-2}\\{1}\end{array}\right]. \nonumber \]

Entonces podemos escribir nuestra solución en el formulario

\[\vec{x}=\vec{x_{p}}+x_{2}\vec{v}. \nonumber \]

Todavía tenemos infinitas soluciones; al elegir un valor para\(x_2\) conseguimos una de estas soluciones. Por ejemplo, al dejar\(x_2= -1\)\(0\), o\(2\), obtenemos las soluciones

\[\left[\begin{array}{c}{5}\\{-1}\end{array}\right],\quad\left[\begin{array}{c}{3}\\{0}\end{array}\right]\quad\text{and}\quad\left[\begin{array}{c}{-1}\\{2}\end{array}\right]. \nonumber \]

Hemos resuelto oficialmente el problema; hemos resuelto la ecuación\(A\vec{x}=\vec{b}\) para\(\vec{x}\) y hemos escrito la solución en forma vectorial. Como ayuda visual adicional, graficaremos esta solución.

Cada vector en la solución se puede escribir como la suma de dos vectores:\(\vec{x_{p}}\) y un múltiplo de\(\vec{v}\). En la Figura\(\PageIndex{3}\),\(\vec{x_{p}}\) se grafica y\(\vec{v}\) se grafica con su origen comenzando en la punta de\(\vec{x_{p}}\). Finalmente, se dibuja una línea en la dirección de\(\vec{v}\) desde la punta de\(\vec{x_{p}}\); cualquier vector que apunte a cualquier punto de esta línea es una solución a\(A\vec{x}=\vec{b}\).

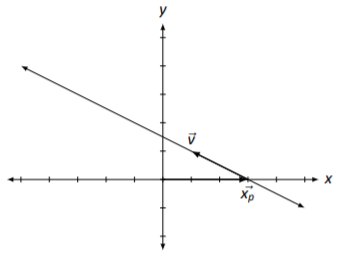
Figura\(\PageIndex{3}\): La solución, como línea, a\(A\vec{x}=\vec{b}\) en Ejemplo\(\PageIndex{4}\).

Los ejemplos anteriores ilustran algunos conceptos importantes. Una es que podemos “ver” la solución a un sistema de ecuaciones lineales de una nueva manera. Antes, cuando teníamos infinitas soluciones, sabíamos que podíamos elegir arbitrariamente valores para nuestras variables libres y obtener diferentes soluciones. Sabíamos que esto era cierto, e incluso lo practicamos, pero el resultado no fue muy “tangible”. Ahora, podemos ver nuestra solución como un vector; al elegir diferentes valores para nuestras variables libres, vemos esto como multiplicar ciertos vectores importantes por un escalar que da una solución diferente.

Otro concepto importante que demuestran estos ejemplos proviene del hecho de que los Ejemplos\(\PageIndex{2}\) y solo\(\PageIndex{4}\) fueron “ligeramente diferentes” y por lo tanto solo tenían respuestas “ligeramente diferentes”. Ambas soluciones tenían

\[x_{2}\left[\begin{array}{c}{-2}\\{1}\end{array}\right] \nonumber \]

en ellos; en Ejemplo\(\PageIndex{4}\) la solución también tenía otro vector agregado a esto. ¿Fue esta coincidencia, o hay un patrón definido aquí?

¡Por supuesto que hay un patrón! Ahora,\(\ldots\) ¿qué es exactamente? Primero, definimos un término.

Definición: Sistema Lineal Homogéneo de Ecuaciones

Un sistema de ecuaciones lineales es homogéneo si las constantes en cada ecuación son cero.

Nota: un sistema homogéneo de ecuaciones se puede escribir en forma vectorial como\(A\vec{x}=\vec{0}\).

El término homogéneo proviene de dos palabras griegas; homo significa “mismo” y género que significa “tipo”. Un sistema homogéneo de ecuaciones es un sistema en el que cada ecuación es del mismo tipo — todas las constantes son 0. Observe que el sistema de ecuaciones en Ejemplos\(\PageIndex{2}\) y\(\PageIndex{4}\) son homogéneos.

Tenga en cuenta que\(A\vec{0}=\vec{0}\); es decir, si establecemos\(\vec{x}=\vec{0}\), tenemos una solución a un conjunto homogéneo de ecuaciones. Este hecho es importante; el vector cero es siempre una solución a un sistema lineal homogéneo. Por lo tanto, un sistema homogéneo siempre es consistente; sólo necesitamos determinar si tenemos exactamente una solución (justa\(\vec{0}\)) o soluciones infinitas. Esta idea es importante así que le damos su propia caja.

Idea Clave\(\PageIndex{1}\): Homogeneous Systems and Consistency

Todos los sistemas lineales homogéneos son consistentes.

¿Cómo determinamos si tenemos exactamente una o infinitas soluciones? Recall Key Idea 1.4.1: si la solución tiene alguna variable libre, entonces tendrá infinitas soluciones. ¿Cómo podemos saber si el sistema tiene variables libres? Formar la matriz aumentada\([A\:\:\vec{0}]\), ponerla en forma de escalón de fila reducida e interpretar el resultado.

Puede parecer que hemos planteado una nueva pregunta: “¿Cuándo\(A\vec{x}=\vec{0}\) tiene exactamente una o infinitas soluciones?” sólo para responder con “Mira la forma de escalón de fila reducida\(A\) e interpreta los resultados, igual que siempre”. ¿Por qué plantear una nueva pregunta si la respuesta es antigua?

Si bien la nueva pregunta tiene una solución antigua, sí lleva a una gran idea. Vamos a refrescar nuestra memoria; antes resolvimos dos sistemas lineales,

\[A\vec{x}=\vec{0}\quad\text{and}\quad A\vec{x}=\vec{b} \nonumber \]

donde

\[A=\left[\begin{array}{cc}{1}&{2}\\{2}&{4}\end{array}\right]\quad\text{and}\quad\vec{b}=\left[\begin{array}{c}{3}\\{6}\end{array}\right]. \nonumber \]

La solución al primer sistema de ecuaciones,\(A\vec{x}=\vec{0}\), es

\[\vec{x}=x_{2}\left[\begin{array}{c}{-2}\\{1}\end{array}\right] \nonumber \]

y la solución al segundo conjunto de ecuaciones,\(A\vec{x}=\vec{b}\), es

\[\vec{x}=\left[\begin{array}{c}{3}\\{0}\end{array}\right]+x_{2}\left[\begin{array}{c}{-2}\\{1}\end{array}\right], \nonumber \]

para todos los valores de\(x_2\).

Recordando nuestra notación utilizada anteriormente, set

\[\vec{x_{p}}=\left[\begin{array}{c}{3}\\{0}\end{array}\right]\quad\text{and let}\quad\vec{v}=\left[\begin{array}{c}{-2}\\{1}\end{array}\right]. \nonumber \]

Así nuestra solución al sistema lineal\(A\vec{x}=\vec{b}\) es

\[\vec{x}=\vec{x_{p}}+x_{2}\vec{v}. \nonumber \]

Veamos cómo funciona exactamente esta solución; veamos por qué\(A\vec{x}\) es igual\(\vec{b}\). Multiplicar\(A\vec{x}\):

\[\begin{align}\begin{aligned}A\vec{x}&=A(\vec{x_{p}}+x_{2}\vec{v}) \\ &=A\vec{x_{p}}+A(x_{2}\vec{v}) \\ &=A\vec{x_{p}}+x_{2}(A\vec{v}) \\ &=A\vec{x_{p}}+x_{2}\vec{0} \\ &=A\vec{x_{p}}+\vec{0} \\ &=A\vec{x_{p}} \\ &=\vec{b}\end{aligned}\end{align} \nonumber \]

Sabemos que la última línea es cierta, eso\(A\vec{x_{p}}=\vec{b}\), ya que sabemos que\(\vec{x}\) fue una solución para\(A\vec{x}=\vec{b}\). El punto es que\(\vec{x_{p}}\) en sí mismo es una solución a\(A\vec{x}=\vec{b}\), y podríamos encontrar más soluciones añadiendo vectores “que van a cero” cuando se multiplican por\(A\). (El subíndice\(p\) de “\(\vec{x_{p}}\)” se utiliza para denotar que este vector es una solución “particular”).

Dicho de otra manera, digamos que sabemos dos cosas: esa\(A\vec{x_{p}}=\vec{b}\) y\(A\vec{v}=\vec{0}\). ¿Qué es\(A(\vec{x_{p}}+\vec{v})\)? Podemos multiplicarlo:

\[\begin{align}\begin{aligned}A(\vec{x_{p}}+\vec{v})&=A\vec{x_{p}}+A\vec{v} \\ &=\vec{b}+\vec{0} \\ &=\vec{b}\end{aligned}\end{align} \nonumber \]

y ver que\(A(\vec{x_{p}}+\vec{v})\) también es igual\(\vec{b}\).

Entonces nos preguntamos: ¿significa esto que\(A\vec{x}=\vec{b}\) tendrá infinitas soluciones? Después de todo, si\(\vec{x_{p}}\) y\(\vec{x_{p}}+\vec{v}\) son ambas soluciones, ¿no tenemos soluciones infinitas?

No. Si\(A\vec{x}=\vec{0}\) tiene exactamente una solución, entonces\(\vec{v}=\vec{0}\), y\(\vec{x_{p}}=\vec{x_{p}}+\vec{v}\); solo tenemos una solución.

Entonces aquí está la culminación de toda nuestra diversión que comenzó unas páginas atrás. Si\(\vec{v}\) es una solución para\(A\vec{x}=\vec{0}\) y\(\vec{x_{p}}\) es una solución para\(A\vec{x}=\vec{b}\), entonces también\(\vec{x_{p}}+\vec{v}\) es una solución para\(A\vec{x}=\vec{b}\). Si\(A\vec{x}=\vec{0}\) tiene infinitas soluciones, también lo hace\(A\vec{x}=\vec{b}\); si solo\(A\vec{x}=\vec{0}\) tiene una solución, también lo hace\(A\vec{x}=\vec{b}\). Esta idea culminante es, por supuesto, lo suficientemente importante como para volver a afirmarse.

Idea Clave\(\PageIndex{2}\): Solutions of Consistent Systems

Let\(A\vec{x}=\vec{b}\) Ser un sistema consistente de ecuaciones lineales.

1. Si\(A\vec{x}=\vec{0}\) tiene exactamente una solución\((\vec{x}=\vec{0})\), entonces\(A\vec{x}=\vec{b}\) tiene exactamente una solución.
2. Si\(A\vec{x}=\vec{0}\) tiene infinitas soluciones, entonces\(A\vec{x}=\vec{b}\) tiene infinitas soluciones.

Una palabra clave en la declaración anterior es consistente. Si\(A\vec{x}=\vec{b}\) es inconsistente (el sistema lineal no tiene solución), entonces no importa cuántas soluciones\(A\vec{x}=\vec{0}\) tenga; no\(A\vec{x}=\vec{b}\) tiene solución.

Suficiente diversión, suficiente teoría. Tenemos que practicar.

Ejemplo\(\PageIndex{5}\)

Let

\[A=\left[\begin{array}{cccc}{1}&{-1}&{1}&{3}\\{4}&{2}&{4}&{6}\end{array}\right]\quad\text{and}\quad\vec{b}=\left[\begin{array}{c}{1}\\{10}\end{array}\right]. \nonumber \]

Resuelva los sistemas lineales\(A\vec{x}=\vec{0}\) y\(A\vec{x}=\vec{b}\) para\(\vec{x}\), y escriba las soluciones en forma vectorial.

Solución

Abordaremos\(A\vec{x}=\vec{0}\) primero. Formamos la matriz aumentada asociada, la ponemos en forma de escalón de fila reducida e interpretamos el resultado.

\[\left[\begin{array}{ccccc}{1}&{-1}&{1}&{3}&{0}\\{4}&{2}&{4}&{6}&{0}\end{array}\right]\quad\vec{\text{rref}}\quad\left[\begin{array}{ccccc}{1}&{0}&{1}&{2}&{0}\\{0}&{1}&{0}&{-1}&{0}\end{array}\right] \nonumber \]

\[\begin{align}\begin{aligned} x_1&=-x_3-2x_4\\x_2 &= x_4\\ x_3&\text{ is free}\\x_4&\text{ is free} \end{aligned}\end{align} \nonumber \]Para escribir nuestra solución en forma vectorial, reescribimos\(x_1\) y\(x_2\)\(\vec{x}\) en términos de\(x_3\) y\(x_4\).

\[\vec{x}=\left[\begin{array}{c}{x_{1}}\\{x_{2}}\\{x_{3}}\\{x_{4}}\end{array}\right]=\left[\begin{array}{c}{-x_{3}-2x_{4}}\\{x_{4}}\\{x_{3}}\\{x_{4}}\end{array}\right] \nonumber \]

Finalmente, “separamos” este vector en dos vectores, uno con las “\(x_3\)cosas” y otro con las “\(x_4\)cosas”.

\[\begin{align}\begin{aligned}\vec{x}&=\left[\begin{array}{c}{-x_{3}-2x_{4}}\\{x_{4}}\\{x_{3}}\\{x_{4}}\end{array}\right] \\ &=\left[\begin{array}{c}{-x_{3}}\\{0}\\{x_{3}}\\{0}\end{array}\right]+\left[\begin{array}{c}{-2x_{4}}\\{x_{4}}\\{0}\\{x_{4}}\end{array}\right] \\ &=x_{3}\left[\begin{array}{c}{-1}\\{0}\\{1}\\{0}\end{array}\right]+x_{4}\left[\begin{array}{c}{-2}\\{1}\\{0}\\{1}\end{array}\right] \\ &=x_{3}\vec{u}+x_{4}\vec{v}\end{aligned}\end{align} \nonumber \]

Usamos\(\vec{u}\) y\(\vec{v}\) simplemente para dar nombres a estos vectores (y ahorrar algo de espacio).

Es fácil confirmar que ambos\(\vec{u}\) y\(\vec{v}\) son soluciones al sistema lineal\(A\vec{x}=\vec{0}\). (Simplemente multiplicar\(A\vec{u}\)\(A\vec{v}\) y ver que ambos son\(\vec{0}\).) Dado que ambas son soluciones a un sistema homogéneo de ecuaciones lineales, cualquier combinación lineal de\(\vec{u}\) y también\(\vec{v}\) será una solución.

Ahora vamos a abordar\(A\vec{x}=\vec{b}\). Una vez más ponemos la matriz aumentada asociada en forma de escalón de fila reducida e interpretamos los resultados.

\[\left[\begin{array}{ccccc}{1}&{-1}&{1}&{3}&{1}\\{4}&{2}&{4}&{6}&{10}\end{array}\right]\quad\vec{\text{rref}}\quad\left[\begin{array}{ccccc}{1}&{0}&{1}&{2}&{2}\\{0}&{1}&{0}&{-1}&{1}\end{array}\right] \nonumber \]

\[\begin{align}\begin{aligned} x_1&=2-x_3-2x_4\\x_2 &= 1+x_4\\ x_3&\text{ is free}\\x_4&\text{ is free} \end{aligned}\end{align} \nonumber \]

Escribir esta solución en forma vectorial da

\[\vec{x}=\left[\begin{array}{c}{x_{1}}\\{x_{2}}\\{x_{3}}\\{x_{4}}\end{array}\right]=\left[\begin{array}{c}{2-x_{3}-2x_{4}}\\{1+x_{4}}\\{x_{3}}\\{x_{4}}\end{array}\right]. \nonumber \]

Nuevamente, separamos este vector, pero esta vez lo dividimos en tres vectores: uno con “\(x_3\)” cosas, uno con “\(x_4\)” cosas, y otro con solo constantes.

\[\begin{align}\begin{aligned}\vec{x}&=\left[\begin{array}{c}{2-x_{3}-2x_{4}}\\{1+x_{4}}\\{x_{3}}\\{x_{4}}\end{array}\right] \\ &=\left[\begin{array}{c}{2}\\{1}\\{0}\\{0}\end{array}\right] + \left[\begin{array}{c}{-x_{3}}\\{0}\\{x_{3}}\\{0}\end{array}\right] +\left[\begin{array}{c}{-2x_{4}}\\{x_{4}}\\{0}\\{x_{4}}\end{array}\right] \\ &=\left[\begin{array}{c}{2}\\{1}\\{0}\\{0}\end{array}\right] +x_{3}\left[\begin{array}{c}{-1}\\{0}\\{1}\\{0}\end{array}\right] + x_{4}\left[\begin{array}{c}{-2}\\{1}\\{0}\\{1}\end{array}\right] \\ &=\underbrace{\vec{x_{p}}}\quad +\quad \underbrace{x_{3}\vec{u}+x_{4}\vec{v}} \\ & \text{particular} \qquad \text{solution to} \\ &\text{solution}\qquad\:\:\text{homogenous} \\ &\qquad\qquad\:\:\:\:\text{equations }A\vec{x}=\vec{0} \end{aligned}\end{align} \nonumber \]

Tenga en cuenta que\(A\vec{x_{p}}=\vec{b}\); por sí mismo,\(\vec{x_{p}}\) es una solución. Para obtener soluciones infinitas, agregamos un montón de cosas que “van a cero” cuando multiplicamos por\(A\); agregamos la solución a las ecuaciones homogéneas.

¿Por qué no graficamos esta solución como lo hicimos en el pasado? Antes solo teníamos dos variables, lo que significa que la solución se podía graficar en 2D. Aquí tenemos cuatro variables, es decir, que nuestra solución “vive” en 4D. Esto se puede dibujar en papel, pero es muy confuso.

Ejemplo\(\PageIndex{6}\)

Reescribir el sistema lineal

\[\begin{array}{ccccccccccc}{x_{1}}&{+}&{2x_{2}}&{-}&{3x_{3}}&{+}&{2x_{4}}&{+}&{7x_{5}}&{=}&{2}\\ {3x_{1}}&{+}&{4x_{2}}&{+}&{5x_{3}}&{+}&{2x_{4}}&{+}&{3x_{5}}&{=}&{-4}\end{array} \nonumber \]

como una ecuación matriz-vector, resolver el sistema usando notación vectorial y dar la solución a las ecuaciones homogéneas relacionadas.

Solución

Reescribiendo el sistema lineal en forma de\(A\vec{x}=\vec{b}\), tenemos que

\[A=\left[\begin{array}{ccccc}{1}&{2}&{-3}&{2}&{7}\\{3}&{4}&{5}&{2}&{3}\end{array}\right],\quad\vec{x}=\left[\begin{array}{c}{x_{1}}\\{x_{2}}\\{x_{3}}\\{x_{4}}\\{x_{5}}\end{array}\right]\quad\text{and}\quad\vec{b}=\left[\begin{array}{c}{2}\\{-4}\end{array}\right]. \nonumber \]

Para resolver el sistema, colocamos la matriz aumentada asociada en forma de escalón de fila reducida e interpretamos los resultados.

\[\left[\begin{array}{cccccc}{1}&{2}&{-3}&{2}&{7}&{2}\\{3}&{4}&{5}&{2}&{3}&{-4}\end{array}\right]\quad\vec{\text{rref}}\quad\left[\begin{array}{cccccc}{1}&{0}&{11}&{-2}&{-11}&{-8}\\{0}&{1}&{-7}&{2}&{9}&{5}\end{array}\right] \nonumber \]

\[\begin{align}\begin{aligned} x_1&=-8-11x_3+2x_4+11x_5\\ x_2&=5+7x_3-2x_4-9x_5\\ x_3&\text{ is free}\\ x_4&\text{ is free}\\ x_5&\text{ is free}\end{aligned}\end{align} \nonumber \]

Utilizamos esta información para escribir\(\vec{x}\), nuevamente separándola. Como tenemos tres variables libres y también constantes, tendremos que separar\(\vec{x}\) en cuatro vectores separados.

\[\begin{align}\begin{aligned}\vec{x}&=\left[\begin{array}{c}{x_{1}}\\{x_{2}}\\{x_{3}}\\{x_{4}}\\{x_{5}}\end{array}\right] \\ &=\left[\begin{array}{c}{-8-11x_{3}+2x_{4}+11x_{5}}\\{5+7x_{3}-2x_{4}-9x_{5}}\\{x_{3}}\\{x_{4}}\\{x_{5}}\end{array}\right] \\ &=\left[\begin{array}{c}{-8}\\{5}\\{0}\\{0}\\{0}\end{array}\right]+\left[\begin{array}{c}{-11x_{3}}\\{7x_{3}}\\{x_{3}}\\{0}\\{0}\end{array}\right]+\left[\begin{array}{c}{2x_{4}}\\{-2x_{4}}\\{0}\\{x_{4}}\\{0}\end{array}\right]+\left[\begin{array}{c}{11x_{5}}\\{-9x_{5}}\\{0}\\{0}\\{x_{5}}\end{array}\right] \\ &=\left[\begin{array}{c}{-8}\\{5}\\{0}\\{0}\\{0}\end{array}\right] +x_{3}\left[\begin{array}{c}{-11}\\{7}\\{1}\\{0}\\{0}\end{array}\right]+x_{4}\left[\begin{array}{c}{2}\\{-2}\\{0}\\{1}\\{0}\end{array}\right]+x_{5}\left[\begin{array}{c}{11}\\{-9}\\{0}\\{0}\\{1}\end{array}\right] \\ &=\underbrace{\vec{x_{p}}}\quad+\quad \underbrace{x_{3}\vec{u}+x_{4}\vec{v}+x_{5}\vec{w}} \\ & \text{particular} \qquad \text{solution to homogenous} \\ &\text{solution}\qquad\quad\text{equations }A\vec{x}=\vec{0} \end{aligned}\end{align} \nonumber \]

Así\(\vec{x_{p}}\) es una solución particular;\(A\vec{x_{p}}=\vec{b}\). (Multiplicarlo para verificar que esto es cierto.) Los otros vectores,\(\vec{u}\),\(\vec{v}\) y\(\vec{w}\), que se multiplican por nuestras variables libres\(x_3\),\(x_4\) y\(x_5\), son cada uno soluciones a las ecuaciones homogéneas,\(A\vec{x}=\vec{0}\). Cualquier combinación lineal de estos tres vectores, es decir, cualquier vector que se encuentre eligiendo valores para\(x_3\),\(x_4\) y\(x_5\) en\(x_{3}\vec{u}+x_{4}\vec{v}+x_{5}\vec{w}\) es una solución para\(A\vec{x}=\vec{0}\).

Ejemplo\(\PageIndex{7}\)

Let

\[A=\left[\begin{array}{cc}{1}&{2}\\{4}&{5}\end{array}\right]\quad\text{and}\quad\vec{b}=\left[\begin{array}{c}{3}\\{6}\end{array}\right]. \nonumber \]

Encuentre las soluciones para\(A\vec{x}=\vec{b}\) y\(A\vec{x}=\vec{0}\).

Solución

Pasamos por el trabajo familiar de encontrar la forma de escalón de fila reducida de la matriz aumentada apropiada e interpretar la solución.

\[\left[\begin{array}{ccc}{1}&{2}&{3}\\{4}&{5}&{6}\end{array}\right]\quad\vec{\text{rref}}\quad\left[\begin{array}{ccc}{1}&{0}&{-1}\\{0}&{1}&{2}\end{array}\right] \nonumber \]

\[\begin{align}\begin{aligned} x_1 &= -1\\x_2 &= 2\end{aligned}\end{align} \nonumber \]

Así

\[\vec{x}=\left[\begin{array}{c}{x_{1}}\\{x_{2}}\end{array}\right]=\left[\begin{array}{c}{-1}\\{2}\end{array}\right]. \nonumber \]

Esto puede parecernos un poco extraño; estamos acostumbrados a tener muchos vectores diferentes en la solución. Sin embargo, en este caso, el sistema lineal\(A\vec{x}=\vec{b}\) tiene exactamente una solución, y la hemos encontrado. ¿Cuál es la solución\(A\vec{x}=\vec{0}\)? Como solo hemos encontrado una solución para\(A\vec{x}=\vec{b}\), podemos concluir a partir de Key\(\PageIndex{2}\) Idea\(A\vec{x}=\vec{0}\) que las ecuaciones homogéneas relacionadas tienen una sola solución, a saber\(\vec{x}=\vec{0}\). Podemos escribir nuestro vector de solución\(\vec{x}\) en una forma similar a nuestros ejemplos anteriores para resaltar esto:

\[\begin{align}\begin{aligned}\vec{x}&=\left[\begin{array}{c}{-1}\\{2}\end{array}\right] \\ &=\left[\begin{array}{c}{-1}\\{2}\end{array}\right] +\left[\begin{array}{c}{0}\\{0}\end{array}\right] \\ &=\underbrace{\vec{x_{p}}}\quad +\quad\underbrace{\vec{0}} \\ &\text{particular}\qquad\text{solution to} \\ &\text{solution}\qquad A\vec{x}=\vec{0}\end{aligned}\end{align} \nonumber \]

Ejemplo\(\PageIndex{8}\)

Let

\[A=\left[\begin{array}{cc}{1}&{1}\\{2}&{2}\end{array}\right]\quad\text{and}\quad\vec{b}=\left[\begin{array}{c}{1}\\{1}\end{array}\right]. \nonumber \]

Encuentre las soluciones para\(A\vec{x}=\vec{b}\) y\(A\vec{x}=\vec{0}\).

Solución

Para resolver\(A\vec{x}=\vec{b}\), ponemos la matriz aumentada apropiada en forma de escalón de fila reducida e interpretamos los resultados.

\[\left[\begin{array}{ccc}{1}&{1}&{1}\\{2}&{2}&{1}\end{array}\right]\quad\vec{\text{rref}}\quad\left[\begin{array}{ccc}{1}&{1}&{0}\\{0}&{0}&{1}\end{array}\right] \nonumber \]

De inmediato tenemos un problema; vemos que la segunda fila nos dice eso\(0x_1+0x_2 = 1\), la señal de que nuestro sistema no tiene solución. Por lo tanto, no\(A\vec{x}=\vec{b}\) tiene solución. Por supuesto, esto no quiere decir que no\(A\vec{x}=\vec{0}\) tenga solución; siempre tiene una solución.

Para encontrar la solución a\(A\vec{x}=\vec{0}\), interpretamos el escalón de fila reducido de la matriz aumentada apropiada.

\[\left[\begin{array}{ccc}{1}&{1}&{0}\\{2}&{2}&{0}\end{array}\right]\quad\vec{\text{rref}}\quad\left[\begin{array}{ccc}{1}&{1}&{0}\\{0}&{0}&{0}\end{array}\right] \nonumber \]

\[\begin{align}\begin{aligned} x_1 &=-x_2 \\ x_2 &\text{ is free} \end{aligned}\end{align} \nonumber \]

Así

\[\begin{align}\begin{aligned}\vec{x}&=\left[\begin{array}{c}{x_{1}}\\{x_{2}}\end{array}\right] \\ &=\left[\begin{array}{c}{-x_{2}}\\{x_{2}}\end{array}\right] \\ &=x_{2}\left[\begin{array}{c}{-1}\\{1}\end{array}\right] \\ &=x_{2}\vec{u}.\end{aligned}\end{align} \nonumber \]

No tenemos solución para\(A\vec{x}=\vec{b}\), sino infinitas soluciones para\(A\vec{x}=\vec{0}\).

El ejemplo anterior puede parecer violar el principio de Idea Clave\(\PageIndex{2}\). Después de todo, parece que tener infinitas soluciones a\(A\vec{x}=\vec{0}\) debería implicar infinitas soluciones a\(A\vec{x}=\vec{b}\). No obstante, nos recordamos la palabra clave en la idea que observamos antes: consistente. Si\(A\vec{x}=\vec{b}\) es consistente y\(A\vec{x}=\vec{0}\) tiene infinitas soluciones, entonces también lo hará\(A\vec{x}=\vec{b}\). Pero si no\(A\vec{x}=\vec{b}\) es consistente, no importa cuántas soluciones\(A\vec{x}=\vec{0}\) tenga;\(A\vec{x}=\vec{b}\) sigue siendo inconsistente.
Toda esta sección destaca un concepto muy importante que no entenderemos completamente hasta después de dos secciones, pero aquí lo vislumbramos. Al resolver cualquier sistema de ecuaciones lineales (que podemos escribir como\(A\vec{x}=\vec{b}\)), si tenemos exactamente una solución, soluciones infinitas, o ninguna solución depende de una propiedad intrínseca de\(A\). Pronto sabremos cuál es esa propiedad; en la siguiente sección resolvemos un problema que introdujimos al inicio de esta sección, cómo resolver ecuaciones matriciales\(AX=B\).