2.3.1: Ejercicios 2.3

Última actualización
Guardar como PDF

Page ID: 116424

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

En Ejercicios$\PageIndex{1}$ -$\PageIndex{4}$, vectores$\vec{x}$ y$\vec{y}$ se dan. Croquis$\vec{x}$$\vec{y}$,,$\vec{x}+\vec{y}$, y$\vec{x}-\vec{y}$ en los mismos ejes cartesianos.

Ejercicio$\PageIndex{1}$

$\vec{x}=\left[\begin{array}{c}{1}\\{1}\end{array}\right],\quad\vec{y}=\left[\begin{array}{c}{-2}\\{3}\end{array}\right]$

Responder

$\vec{x}+\vec{y}=\left[\begin{array}{c}{-1}\\{4}\end{array}\right],\quad\vec{x}-\vec{y}=\left[\begin{array}{c}{3}\\{-2}\end{array}\right]$

Los bocetos variarán dependiendo de la elección de origen de cada vector.

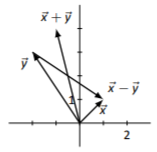
$clipboard_eb6afde601d93e3eecbf4c5e3b6d0fda8.png$

Figura$\PageIndex{1}$

Ejercicio$\PageIndex{2}$

$\vec{x}=\left[\begin{array}{c}{3}\\{1}\end{array}\right],\quad\vec{y}=\left[\begin{array}{c}{1}\\{-2}\end{array}\right]$

Responder

$\vec{x}+\vec{y}=\left[\begin{array}{c}{4}\\{-1}\end{array}\right],\quad\vec{x}-\vec{y}=\left[\begin{array}{c}{2}\\{3}\end{array}\right]$

Los bocetos variarán dependiendo de la elección de origen de cada vector.

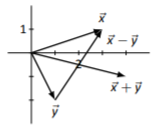
$clipboard_e50ab5c5fd94da72dd50ca5c4487ad15c.png$

Figura$\PageIndex{2}$

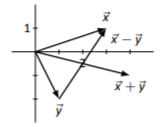
Ejercicio$\PageIndex{3}$

$\vec{x}=\left[\begin{array}{c}{-1}\\{1}\end{array}\right],\quad\vec{y}=\left[\begin{array}{c}{-2}\\{2}\end{array}\right]$

Responder

$\vec{x}+\vec{y}=\left[\begin{array}{c}{-3}\\{3}\end{array}\right],\quad\vec{x}-\vec{y}=\left[\begin{array}{c}{1}\\{-1}\end{array}\right]$

Los bocetos variarán dependiendo de la elección de origen de cada vector.

$clipboard_e4be8d13f77b537ea8af36f89380ff0dc.png$

Figura$\PageIndex{3}$

Ejercicio$\PageIndex{4}$

$\vec{x}=\left[\begin{array}{c}{2}\\{0}\end{array}\right],\quad\vec{y}=\left[\begin{array}{c}{1}\\{3}\end{array}\right]$

Contestar

$\vec{x}+\vec{y}=\left[\begin{array}{c}{3}\\{3}\end{array}\right],\quad\vec{x}-\vec{y}=\left[\begin{array}{c}{1}\\{-3}\end{array}\right]$

Los bocetos variarán dependiendo de la elección de origen de cada vector.

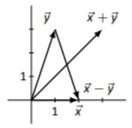
$clipboard_e881e342a01d3c4b9a6ba524bc3afe08d.png$

Figura$\PageIndex{4}$

En Ejercicios$\PageIndex{5}$ —$\PageIndex{8}$,$\vec{y}$ se dibujan vectores$\vec{x}$ y. Croquis$2\vec{x}-\vec{y}$,$\vec{x}+\vec{y}$,$\vec{x}-\vec{y}$ sobre los mismos ejes cartesianos.

Ejercicio$\PageIndex{5}$

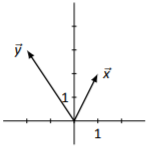
$clipboard_e9a1257242344e3758c7ae7d5a3d18842.png$

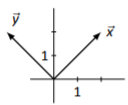
Figura$\PageIndex{5}$

Contestar

Los bocetos variarán dependiendo de la elección de origen de cada vector.

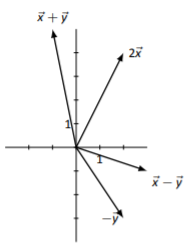
$clipboard_e28bc043d0c6546e81e4aa1e42c7344ee.png$

Figura$\PageIndex{6}$

Ejercicio$\PageIndex{6}$

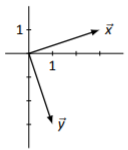
$clipboard_e4e9e6251b4dcf271e722d9ba64cabf3d.png$

Figura$\PageIndex{7}$

Contestar

Los bocetos variarán dependiendo de la elección de origen de cada vector.

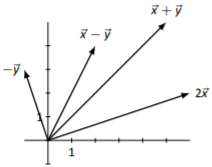
$clipboard_e40ca7a96320c26503bf70cd9f5a09640.png$

Figura$\PageIndex{8}$

Ejercicio$\PageIndex{7}$

$clipboard_ef3c7212e26e117cbe4622858a2674fe6.png$

Figura$\PageIndex{9}$

Contestar

Los bocetos variarán dependiendo de la elección de origen de cada vector.

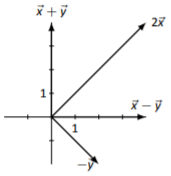
$clipboard_eca2094ba3146a48775d6b127166a8ccb.png$

Figura$\PageIndex{10}$

Ejercicio$\PageIndex{8}$

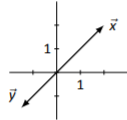
$clipboard_e54154257296c11a359cd4e3d9d469ad4.png$

Figura$\PageIndex{11}$

Contestar

Los bocetos variarán dependiendo de la elección de origen de cada vector.

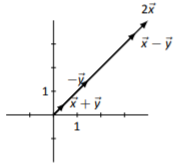
$clipboard_ef1e5163f7fabc779e9652408b895a6f6.png$

Figura$\PageIndex{12}$

En Ejercicios$\PageIndex{9}$ -$\PageIndex{12}$, se dan un vector$\vec{x}$ y un escalar$a$. Usando Definition Vector Length calcula las longitudes de$\vec{x}$ y$a\vec{x}$, luego compara estas longitudes.

Ejercicio$\PageIndex{9}$

$\vec{x}=\left[\begin{array}{c}{2}\\{1}\end{array}\right],\quad a=3$

Contestar: $||\vec{x}||=\sqrt{5};\: ||a\vec{x}||=\sqrt{45}=3\sqrt{5}$. El vector$a\vec{x}$ es$3$ veces tan largo como$\vec{x}$.

Ejercicio$\PageIndex{10}$

$\vec{x}=\left[\begin{array}{c}{4}\\{7}\end{array}\right],\quad a=-2$

Contestar: $||\vec{x}||=\sqrt{65};\: ||a\vec{x}||=\sqrt{260}=2\sqrt{65}$. El vector$a\vec{x}$ es$2$ veces tan largo como$\vec{x}$.

Ejercicio$\PageIndex{11}$

$\vec{x}=\left[\begin{array}{c}{-3}\\{5}\end{array}\right],\quad a=-1$

Contestar: $||\vec{x}||=\sqrt{34};\: ||a\vec{x}||=\sqrt{34}$. Los vectores$a\vec{x}$ y$\vec{x}$ son de la misma longitud (simplemente apuntan en direcciones opuestas).

Ejercicio$\PageIndex{12}$

$\vec{x}=\left[\begin{array}{c}{3}\\{-9}\end{array}\right],\quad a=\frac{1}{3}$

Contestar: $||\vec{x}||=\sqrt{90}=3\sqrt{10};\: ||a\vec{x}||=\sqrt{10}$. El vector$a\vec{x}$ es un tercio de la longitud de$\vec{x}$; equivalentemente,$\vec{x}$ es$3$ veces tan largo como$a\vec{x}$.

Ejercicio$\PageIndex{13}$

Cuatro pares de vectores$\vec{x}$ y$\vec{y}$ se dan a continuación. Para cada par, computar$||\vec{x}||$,$||\vec{y}||$, y$||\vec{x}+\vec{y}||$. Usa esta información para responder: ¿Siempre, a veces, o nunca es cierto eso$||\vec{x}||+||\vec{y}||=||\vec{x}+\vec{y}||$? Si siempre o nunca es cierto, explique por qué. Si a veces es cierto, explique cuándo es verdad.

$\vec{x}=\left[\begin{array}{c}{1}\\{1}\end{array}\right],\quad\vec{y}=\left[\begin{array}{c}{2}\\{3}\end{array}\right]$
$\vec{x}=\left[\begin{array}{c}{1}\\{-2}\end{array}\right],\quad\vec{y}=\left[\begin{array}{c}{3}\\{-6}\end{array}\right]$
$\vec{x}=\left[\begin{array}{c}{-1}\\{3}\end{array}\right],\quad\vec{y}=\left[\begin{array}{c}{2}\\{5}\end{array}\right]$
$\vec{x}=\left[\begin{array}{c}{2}\\{1}\end{array}\right],\quad\vec{y}=\left[\begin{array}{c}{-4}\\{-2}\end{array}\right]$

Contestar

$||\vec{x}||=\sqrt{2};\: ||\vec{y}||=\sqrt{13};\: ||\vec{x}+\vec{y}||=5$.
$||\vec{x}||=\sqrt{5};\: ||\vec{y}||=3\sqrt{5};\: ||\vec{x}+\vec{y}||=4\sqrt{5}$.
$||\vec{x}||=\sqrt{10};\: ||\vec{y}||=\sqrt{29};\: ||\vec{x}+\vec{y}||=\sqrt{65}$.
$||\vec{x}||=\sqrt{5};\: ||\vec{y}||=2\sqrt{5};\: ||\vec{x}+\vec{y}||=\sqrt{5}$.

La igualdad se mantiene a veces; sólo cuando$\vec{x}$ y$\vec{y}$ apuntar a lo largo de la misma línea, en la misma dirección.

En Ejercicios$\PageIndex{14}$ -$\PageIndex{17}$,$A$ se da una matriz. Croquis$\vec{x}$$\vec{y}$,,$A\vec{x}$ y$A\vec{y}$ en los mismos ejes cartesianos, donde

\[\vec{x}=\left[\begin{array}{c}{1}\\{1}\end{array}\right]\quad\text{and}\quad\vec{y}=\left[\begin{array}{c}{-1}\\{2}\end{array}\right]\nonumber \]

Ejercicio$\PageIndex{14}$

$A=\left[\begin{array}{cc}{1}&{-1}\\{2}&{3}\end{array}\right]$

Contestar

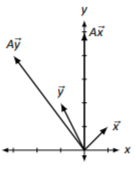
$clipboard_eb8b3bc5c904ff285e713c8b3d1d33e83.png$

Figura$\PageIndex{13}$

Ejercicio$\PageIndex{15}$

$A=\left[\begin{array}{cc}{2}&{0}\\{-1}&{3}\end{array}\right]$

Contestar

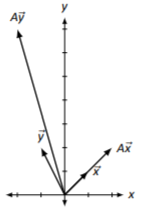
$clipboard_e7967cac33255a511639e33dcf7a32ae5.png$

Figura$\PageIndex{14}$

Ejercicio$\PageIndex{16}$

$A=\left[\begin{array}{cc}{1}&{1}\\{1}&{1}\end{array}\right]$

Contestar

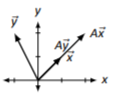
$clipboard_e219599a02a9c6f12a0bbd8ea542f9c04.png$

Figura$\PageIndex{15}$

Ejercicio$\PageIndex{17}$

$A=\left[\begin{array}{cc}{1}&{2}\\{-1}&{-2}\end{array}\right]$

Contestar

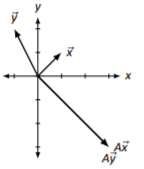
$clipboard_e90e6b48da32ca970fec11a418c19acf5.png$

Figura$\PageIndex{16}$

Ejercicio\(\PageIndex{1}\)

Ejercicio\(\PageIndex{2}\)

Ejercicio\(\PageIndex{3}\)

Ejercicio\(\PageIndex{4}\)

Ejercicio\(\PageIndex{5}\)

Ejercicio\(\PageIndex{6}\)

Ejercicio\(\PageIndex{7}\)

Ejercicio\(\PageIndex{8}\)

Ejercicio\(\PageIndex{9}\)

Ejercicio\(\PageIndex{10}\)

Ejercicio\(\PageIndex{11}\)

Ejercicio\(\PageIndex{12}\)

Ejercicio\(\PageIndex{13}\)

Ejercicio\(\PageIndex{14}\)

Ejercicio\(\PageIndex{15}\)

Ejercicio\(\PageIndex{16}\)

Ejercicio\(\PageIndex{17}\)