5.2: Propiedades de las Transformaciones Lineales

Objetivos de aprendizaje

• T/F: Trasladar las\(2\) unidades del plano cartesiano hacia arriba es una transformación lineal.
• T/F: Si\(T\) es una transformación lineal, entonces\(T(\vec{0})=\vec{0}\).

En la sección anterior discutimos las transformaciones estándar del plano cartesiano —rotaciones, reflexiones, etc. Como ejemplo motivacional para el estudio de esta sección, consideremos otra transformación— encontremos la matriz que mueve la unidad cuadrada una unidad a la derecha (ver Figura\(\PageIndex{1}\)). Esto se llama traducción.

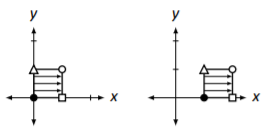
Figura\(\PageIndex{1}\): Trasladando el cuadrado de la unidad una unidad a la derecha.

Nuestro trabajo de la sección anterior nos permite encontrar la matriz rápidamente. Al mirar la imagen, es fácil ver que\(\vec{e_{1}}\) se mueve\(\left[\begin{array}{c}{2}\\{0}\end{array}\right]\) y\(\vec{e_{2}}\) se mueve a\(\left[\begin{array}{c}{1}\\{1}\end{array}\right]\). Por lo tanto, la matriz de transformación debe ser

\[A=\left[\begin{array}{cc}{2}&{1}\\{0}&{1}\end{array}\right].\nonumber \]

No obstante, fíjese en la Figura\(\PageIndex{2}\) donde se dibuja el cuadrado unitario después de ser transformado por\(A\). Es claro que no obtuvimos el resultado deseado; la unidad cuadrada no fue traducida, sino estirada/esquilada de alguna manera.

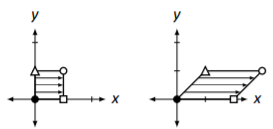
Figura\(\PageIndex{2}\): Transformación real de la unidad cuadrada por matriz\(A\).

¿Qué hicimos mal? Vamos a responder a esta pregunta, pero primero necesitamos desarrollar algunos pensamientos y términos de vocabulario.

Hemos estado usando el término “transformación” para describir cómo hemos cambiado los vectores. De hecho, “transformación” es sinónimo de “función”. Estamos acostumbrados a funciones como\(f(x) = x^2\), donde la entrada es un número y la salida es otro número. En la sección anterior, aprendimos sobre transformaciones (funciones) donde la entrada era un vector y la salida era otro vector. Si\(A\) es una “matriz de transformación”, entonces podríamos crear una función de la forma\(T(\vec{x})=A\vec{x}\). Es decir, un vector\(\vec{x}\) es la entrada, y la salida se\(\vec{x}\) multiplica por\(A\). \(^{1}\)

Cuando definimos\(f(x) = x^2\) anteriormente, dejamos que el lector asuma que la entrada era efectivamente un número. Si quisiéramos estar completos, deberíamos haber declarado\[f:\mathbb{R} \to\mathbb{R} \quad \text{ where } \quad f(x)=x^2.\nonumber \] La primera parte de esa línea nos decía que la entrada era un número real (ese era el primero\(\mathbb{R}\)) y la salida también era un número real (el segundo\(\mathbb{R}\)).

Para definir una transformación donde un vector 2D se transforma en otro vector 2D a través de la multiplicación por una\(2\times 2\) matriz\(A\), debemos escribir

\[T:\mathbb{R}^{2}\to\mathbb{R}^{2}\quad\text{where}\quad T(\vec{x})=A\vec{x}.\nonumber \]

Aquí, el primero\(\mathbb{R}^{2}\) significa que estamos usando vectores 2D como nuestra entrada, y el segundo\(\mathbb{R}^{2}\) significa que un vector 2D es la salida.

Considera un ejemplo rápido:

\[T:\mathbb{R}^{2}\to\mathbb{R}^{3}\quad\text{where}\quad T\left(\left[\begin{array}{c}{x_{1}}\\{x_{2}}\end{array}\right]\right)=\left[\begin{array}{c}{x_{1}^{2}}\\{2x_{1}}\\{x_{1}x_{2}}\end{array}\right].\nonumber \]

Observe que esto toma vectores 2D como entrada y devuelve vectores 3D como salida. Por ejemplo,

\[T\left(\left[\begin{array}{c}{3}\\{-2}\end{array}\right]\right)=\left[\begin{array}{c}{9}\\{6}\\{-6}\end{array}\right].\nonumber \]

Ahora definimos un tipo especial de transformación (función).

Definición: Transformación lineal

Una transformación\(T:\mathbb{R}^{n}\to\mathbb{R}^{m}\) es una transformación lineal si satisface las dos propiedades siguientes:

1. \(T(\vec{x}+\vec{y})=T(\vec{x})+T(\vec{y})\)para todos los vectores\(\vec{x}\) y\(\vec{y}\), y
2. \(T(k\vec{x})=kT(\vec{x})\)para todos los vectores\(\vec{x}\) y todos los escalares\(k\).

Si\(T\) es una transformación lineal, a menudo se dice que “\(T\)es lineal”.

Aprendamos sobre esta definición a través de algunos ejemplos.

Ejemplo\(\PageIndex{1}\)

Determinar si la transformación\(T:\mathbb{R}^{2}\to\mathbb{R}^{3}\) es o no una transformación lineal, donde

\[T\left(\left[\begin{array}{c}{x_{1}}\\{x_{2}}\end{array}\right]\right)=\left[\begin{array}{c}{x_{1}^{2}}\\{2x_{1}}\\{x_{1}x_{2}}\end{array}\right].\nonumber \]

Solución

Escogeremos arbitrariamente dos vectores\(\vec{x}\) y\(\vec{y}\):

\[\vec{x}=\left[\begin{array}{c}{3}\\{-2}\end{array}\right]\quad\text{and}\quad\vec{y}=\left[\begin{array}{c}{1}\\{5}\end{array}\right].\nonumber \]

Comprobemos para ver si\(T\) es lineal usando la definición.

1. ¿Es\(T(\vec{x}+\vec{y}) = T(\vec{x})+T(\vec{y})\)? Primero,
   \[\vec{x}+\vec{y}=\left[\begin{array}{c}{3}\\{-2}\end{array}\right]+\left[\begin{array}{c}{1}\\{5}\end{array}\right]=\left[\begin{array}{c}{4}\\{3}\end{array}\right].\nonumber \]
   cómpule\(\vec{x}+\vec{y}\): Ahora compute\(T(\vec{x})\)\(T(\vec{y})\), y\(T(\vec{x}+\vec{y})\):

\[\begin{array}{ccccc}{\begin{aligned}T(\vec{x})&=T\left(\left[\begin{array}{c}{3}\\{-2}\end{array}\right]\right) \\ &=\left[\begin{array}{c}{9}\\{6}\\{-6}\end{array}\right]\end{aligned}}&{\quad}&{\begin{aligned}T(\vec{y})&=T\left(\left[\begin{array}{c}{1}\\{5}\end{array}\right]\right) \\ &=\left[\begin{array}{c}{1}\\{2}\\{5}\end{array}\right]\end{aligned}}&{\quad}&{\begin{aligned}T(\vec{x}+\vec{y})&=T\left(\left[\begin{array}{c}{4}\\{3}\end{array}\right]\right) \\ &=\left[\begin{array}{c}{16}\\{8}\\{12}\end{array}\right]\end{aligned}}\end{array}\nonumber \]

¿Es\(T(\vec{x}+\vec{y}) = T(\vec{x})+T(\vec{y})\)?

\[\left[\begin{array}{c}{9}\\{6}\\{-6}\end{array}\right]+\left[\begin{array}{c}{1}\\{2}\\{5}\end{array}\right]\stackrel{!}{\neq} \left[\begin{array}{c}{16}\\{8}\\{12}\end{array}\right].\nonumber \]

Por lo tanto, no\(T\) es una transformación lineal.

Entonces tenemos un ejemplo de algo que no funciona. Intentemos un ejemplo donde las cosas sí funcionan. \(^{2}\)

Ejemplo\(\PageIndex{2}\)

Determinar si la transformación\(T\):\(\mathbb{R}^{2}\to\mathbb{R}^{2}\) es o no una transformación lineal, donde\(T(\vec{x})=A\vec{x}\) y

\[A=\left[\begin{array}{cc}{1}&{2}\\{3}&{4}\end{array}\right].\nonumber \]

Solución

Empecemos por considerar de nuevo arbitrario\(\vec{x}\) y\(\vec{y}\). Vamos a elegir lo mismo\(\vec{x}\) y\(\vec{y}\) de Ejemplo\(\PageIndex{1}\).

\[\vec{x}=\left[\begin{array}{c}{3}\\{-2}\end{array}\right]\quad\text{and}\quad\vec{y}=\left[\begin{array}{c}{1}\\{5}\end{array}\right].\nonumber \]

Si las propiedades de linealidad se mantienen para estos vectores, entonces tal vez en realidad sea lineal (y haremos más trabajo).

1. ¿Es\(T(\vec{x}+\vec{y}) = T(\vec{x})+T(\vec{y})\)? Recordemos:
   \[\vec{x}+\vec{y}=\left[\begin{array}{c}{4}\\{3}\end{array}\right].\nonumber \]
   Ahora computa\(T(\vec{x})\)\(T(\vec{y})\),, y\(T(\vec{x})+T(\vec{y})\):
   \[\begin{array}{ccccc}{\begin{aligned}T(\vec{x})&=T\left(\left[\begin{array}{c}{3}\\{-2}\end{array}\right]\right) \\ &=\left[\begin{array}{c}{-1}\\{1}\end{array}\right]\end{aligned}}&{\quad}&{\begin{aligned}T(\vec{y})&=T\left(\left[\begin{array}{c}{1}\\{5}\end{array}\right]\right) \\ &=\left[\begin{array}{c}{11}\\{23}\end{array}\right]\end{aligned}}&{\quad}&{\begin{aligned}T(\vec{x}+\vec{y})&=T\left(\left[\begin{array}{c}{4}\\{3}\end{array}\right]\right) \\ &=\left[\begin{array}{c}{10}\\{24}\end{array}\right]\end{aligned}}\end{array}\nonumber \]
   Es\(T(\vec{x}+\vec{y})=T(\vec{x})+T(\vec{y})\).
   \[\left[\begin{array}{c}{-1}\\{1}\end{array}\right]+\left[\begin{array}{c}{11}\\{23}\end{array}\right]\stackrel{!}{=}\left[\begin{array}{c}{10}\\{24}\end{array}\right].\nonumber \]
   Hasta el momento, tan bueno:\(T(\vec{x}+\vec{y})\) es igual a\(T(\vec{x})+T(\vec{y})\).
2. ¿Es\(T(k\vec{x}) = kT(\vec{x})\)? Escojamos arbitrariamente\(k=7\), y utilicemos\(\vec{x}\) como antes.
   \[\begin{align*}\begin{aligned}T(7\vec{x})&=T\left(\left[\begin{array}{c}{21}\\{-14}\end{array}\right]\right) \\ &=\left[\begin{array}{c}{-7}\\{7}\end{array}\right] \\ &=7\left[\begin{array}{c}{-1}\\{1}\end{array}\right] \\ &=7\cdot T(\vec{x}) !\end{aligned}\end{align*}\nonumber \]
   Hasta el momento parece que efectivamente\(T\) es lineal, pues funcionó en un ejemplo con vectores elegidos arbitrariamente y escalares. Ahora tenemos que tratar de demostrar que siempre es cierto.
   Considerar\(T(\vec{x}+\vec{y})\). Por la definición de\(T\), tenemos
   \[T(\vec{x}+\vec{y}) = A(\vec{x}+\vec{y}).\nonumber \]
   Por Teorema 2.2.1, parte 2 afirmamos que la Propiedad Distributiva se mantiene para la multiplicación matricial. \(^{3}\)Entonces\(A(\vec{x}+\vec{y}) = A\vec{x} +A\vec{y}\). ¡Reconoce ahora que esta última parte es justa\(T(\vec{x}) + T(\vec{y})\)! Repetimos los pasos anteriores, todos juntos:
   \[\begin{align*}\begin{aligned}T(\vec{x}+\vec{y})&=A(\vec{x}+\vec{y}) &\text{(by the definition of }T\text{ in this example)} \\ &=A\vec{x}+A\vec{y}&\text{(by the Distributive Property)} \\ &=T(\vec{x})+T(\vec{y}) &\text{(again, by the definition of }T\text{)}\end{aligned}\end{align*}\nonumber \]
   Por lo tanto, no importa qué\(\vec{x}\) y\(\vec{y}\) sean elegidos,\(T(\vec{x}+\vec{y}) = T(\vec{x}) + T(\vec{y})\). Así se satisface la primera parte de la definición de linealidad.
   La segunda parte está satisfecha de manera similar. \(k\)Sea un escalar, y considerar:
   \[\begin{align*}\begin{aligned}T(k\vec{x})&=A(k\vec{x}) &\text{(by the definition of }T\text{ is this example)} \\ &=kA\vec{x} &\text{(by Theorem 2.2.1 part 3)} \\ &=kT(\vec{x}) &\text{(again, by the definition of }T\text{)}\end{aligned}\end{align*}\nonumber \]
   Dado que\(T\) satisface ambas partes de la definición, concluimos que\(T\) es una transformación lineal.

Hemos visto hasta ahora dos ejemplos de transformaciones, una que no era lineal y otra que lo era. Uno podría preguntarse “¿Por qué es importante la linealidad?” , que abordaremos en breve.

Primero, consideremos cómo probamos que la transformación en Ejemplo\(\PageIndex{2}\) fue lineal. Definimos\(T\) por multiplicación matricial, es decir,\(T(\vec{x}) = A\vec{x}\). Demostramos que\(T\) era lineal usando propiedades de multiplicación matricial — ¡nunca consideramos los valores específicos de\(A\)! Es decir, no solo elegimos una buena matriz para\(T\); cualquier matriz\(A\) habría funcionado. Esto nos lleva a un teorema importante. La primera parte esencialmente la acabamos de probar; la segunda parte no la vamos a probar, aunque su verdad es muy poderosa.

Teorema\(\PageIndex{1}\): Matrices and Linear Transformations

1. Definir\(T\):\(\mathbb{R}^{n}\to\mathbb{R}^{m}\) por\(T(\vec{x})=A\vec{x}\), donde\(A\) es una\(m\times n\) matriz. Entonces\(T\) es una transformación lineal.
2. Dejar\(T\):\(\mathbb{R}^{n}\to\mathbb{R}^{m}\) ser cualquier transformación lineal. Entonces existe una\(m\times n\) matriz única\(A\) tal que\(T(\vec{x})=A\vec{x}\).

La segunda parte del teorema dice que todas las transformaciones lineales pueden describirse usando la multiplicación matricial. Dada cualquier transformación lineal, existe una matriz que define completamente esa transformación. Esta importante matriz recibe su propio nombre.

Definición: Matriz estándar de una transformación lineal

Dejar\(T\):\(\mathbb{R}^{n}\to\mathbb{R}^{m}\) ser una transformación lineal. Por teorema\(\PageIndex{1}\), hay una matriz\(A\) tal que\(T(\vec{x})=A\vec{x}\). Esta matriz\(A\) se llama la matriz estándar de la transformación lineal\(T\), y se denota\([ T ]\). \(^{a}\)

\(\rule{5cm}{0.4pt}\)

[a] La matriz, como corchetes alrededor,\(T\) sugieren que la matriz estándar\(A\) es una matriz “con\(T\) interior”.

Si bien explorar todas las ramificaciones del Teorema\(\PageIndex{1}\) está fuera del alcance de este texto, que sea suficiente decir que ya que 1) las transformaciones lineales son muy, muy importantes en economía, ciencia, ingeniería y matemáticas, y 2) la teoría de las matrices está bien desarrollada y fácil de implementar a mano y en computadoras, entonces 3) es una gran noticia que estos dos conceptos vayan de la mano.

Ya hemos utilizado en pequeña medida la segunda parte de este teorema. En la sección anterior observamos las transformaciones gráficamente y encontramos las matrices que las produjeron. En su momento, no nos dimos cuenta de que estas transformaciones eran lineales, pero sí lo eran.

Esto nos devuelve al ejemplo motivador con el que iniciamos esta sección. Intentamos encontrar la matriz que tradujo la unidad cuadrada una unidad a la derecha. Nuestro intento fracasó, y aún tenemos que determinar por qué. Dado nuestro vínculo entre matrices y transformaciones lineales, la respuesta es probablemente “la transformación de traducción no es una transformación lineal”. Si bien esa es una afirmación verdadera, en realidad no explica las cosas tan bien. ¿Hay alguna manera de que pudiéramos haber reconocido que esta transformación no era lineal? \(^{4}\)

Sí, la hay. Consideremos la segunda parte de la definición de transformación lineal. Afirma que\(T(k\vec{x}) = kT(\vec{x})\) para todos los escalares\(k\). Si lo dejamos\(k=0\), tenemos\(T(0\vec{x}) = 0\cdot T(\vec{x})\), o más simplemente,\(T(\vec{0}) =\vec{0}\). Es decir, si\(T\) va a ser una transformación lineal, debe enviar el vector cero al vector cero.

Esta es una manera rápida de ver que la transformación de la traducción no logra ser lineal. Al desplazar la unidad cuadrada a la derecha una unidad, la esquina en el punto\((0,0)\) fue enviada al punto\((1,0)\), es decir,

\[\text{the vector }\left[\begin{array}{c}{0}\\{0}\end{array}\right]\text{ was sent to the vector }\left[\begin{array}{c}{1}\\{0}\end{array}\right].\nonumber \]

Esta propiedad relacionada con\(\vec{0}\) es importante, por lo que la destacamos aquí.

Idea Clave\(\PageIndex{1}\): Linear Transformations and \(\vec{0}\)

Dejar\(T\):\(\mathbb{R}^{n}\to\mathbb{R}^{m}\) ser una transformación lineal. Entonces:

\[T(\vec{0_{n}})=\vec{0_{m}}.\nonumber \]

Es decir, el vector cero en\(\mathbb{R}^{n}\) se envía al vector cero en\(\mathbb{R}^{m}\).

El lector interesado tal vez desee leer la nota al pie de página a continuación. \(^{5}\)

La matriz estándar de una transformación lineal

A menudo ocurre que si bien uno puede describir una transformación lineal, uno no sabe qué matriz realiza esa transformación (es decir, uno no conoce la matriz estándar de esa transformación lineal). ¿Cómo lo encontramos sistemáticamente? Necesitaremos una nueva definición.

Definición: Vectores de Unidad Standad

En\(\mathbb{R}^{n}\), los vectores unitarios estándar\(\vec{e_{i}}\) son los vectores con a\(1\) en la\(i^{\text{th}}\) entrada y\(0\) s en todas partes.

Ya hemos visto estos vectores en la sección anterior. En\(\mathbb{R}^{2}\), identificamos

\[\vec{e_{1}}=\left[\begin{array}{c}{1}\\{0}\end{array}\right]\quad\text{and}\quad\vec{e_{2}}=\left[\begin{array}{c}{0}\\{1}\end{array}\right].\nonumber \]

En\(\mathbb{R}^{4}\), hay vectores de unidad\(4\) estándar:

\[\vec{e_{1}}=\left[\begin{array}{c}{1}\\{0}\\{0}\\{0}\end{array}\right],\quad\vec{e_{2}}=\left[\begin{array}{c}{0}\\{1}\\{0}\\{0}\end{array}\right],\quad\vec{e_{3}}=\left[\begin{array}{c}{0}\\{0}\\{1}\\{0}\end{array}\right],\quad\text{and}\quad\vec{e_{4}}=\left[\begin{array}{c}{0}\\{0}\\{0}\\{1}\end{array}\right].\nonumber \]

¿Cómo nos ayudan estos vectores a encontrar la matriz estándar de una transformación lineal? Recordemos nuevamente nuestro trabajo en el apartado anterior. Allí, practicamos mirar el cuadrado unitario transformado y deducir la matriz de transformación estándar\(A\). Esto lo hicimos haciendo la primera columna\(A\) del vector donde\(\vec{e_{1}}\) terminó y haciendo la segunda columna\(A\) del vector donde\(\vec{e_{2}}\) terminó. Uno podría representar esto con:

\[A=[T(\vec{e_{1}})\:\: T(\vec{e_{2}})]=[T].\nonumber \]

Es decir,\(T(\vec{e_{1}})\) es el vector donde\(\vec{e_{1}}\) termina, y\(T(\vec{e_{2}})\) es el vector donde\(\vec{e_{2}}\) termina.

Lo mismo es cierto en general. Dada una transformación lineal\(T:\mathbb{R}^{n}\to\mathbb{R}^{m}\), la matriz estándar de\(T\) es la matriz cuya\(i^\text{th}\) columna es el vector donde\(\vec{e_{i}}\) termina. Si bien no vamos a probar que esto es cierto, lo es, y es muy útil. Por lo tanto volveremos a declararlo como teorema.

Teorema\(\PageIndex{2}\)

La Matriz Estándar de una Transformación Lineal

Dejar\(T\):\(\mathbb{R}^{n}\to\mathbb{R}^{m}\) ser una transformación lineal. Entonces\([T]\) está la\(m\times n\) matriz:

\[[T]=[T(\vec{e_{1}})\:\:T(\vec{e_{2}})\:\cdots\: T(\vec{e_{n}})].\nonumber \]

Practicemos este teorema en un ejemplo.

Ejemplo\(\PageIndex{3}\)

\(\mathbb{R}^{3}\to\mathbb{R}^{4}\)Definir\(T\): ser la transformación lineal donde

\[T\left(\left[\begin{array}{c}{x_{1}}\\{x_{2}}\\{x_{3}}\end{array}\right]\right)=\left[\begin{array}{c}{x_{1}+x_{2}}\\{3x_{1}-x_{3}}\\{2x_{2}+5x_{3}}\\{4x_{1}+3x_{2}+2x_{3}}\end{array}\right].\nonumber \]

Encuentra\([T]\).

Solución

\(T\)toma vectores de\(\mathbb{R}^{3}\) dentro\(\mathbb{R}^{4}\), así que\([\, T \, ]\) va a ser una\(4\times 3\) matriz. Tenga en cuenta que

\[\vec{e_{1}}=\left[\begin{array}{c}{1}\\{0}\\{0}\end{array}\right],\quad\vec{e_{2}}=\left[\begin{array}{c}{0}\\{1}\\{0}\end{array}\right]\quad\text{and}\quad\vec{e_{3}}=\left[\begin{array}{c}{0}\\{0}\\{1}\end{array}\right].\nonumber \]

Encontramos las columnas de\([T]\) encontrando dónde\(\vec{e_{1}}\),\(\vec{e_{2}}\) y\(\vec{e_{3}}\) se envían, es decir, encontramos\(T(\vec{e_{1}})\),\(T(\vec{e_{2}})\) y\(T(\vec{e_{3}})\).

\[\begin{array}{ccccc}{\begin{aligned}T(\vec{e_{1}})&=T\left(\left[\begin{array}{c}{1}\\{0}\\{0}\end{array}\right]\right) \\ &=\left[\begin{array}{c}{1}\\{3}\\{0}\\{4}\end{array}\right]\end{aligned}}&{\quad}&{\begin{aligned}T(\vec{e_{2}})&=T\left(\left[\begin{array}{c}{0}\\{1}\\{0}\end{array}\right]\right) \\ &=\left[\begin{array}{c}{1}\\{0}\\{2}\\{3}\end{array}\right]\end{aligned}}&{\quad}&{\begin{aligned}T(\vec{e_{3}})&=T\left(\left[\begin{array}{c}{0}\\{0}\\{1}\end{array}\right]\right) \\ &=\left[\begin{array}{c}{0}\\{-1}\\{5}\\{2}\end{array}\right]\end{aligned}}\end{array}\nonumber \]

Por lo tanto

\[[T]=A=\left[\begin{array}{ccc}{1}&{1}&{0}\\{3}&{0}&{-1}\\{0}&{2}&{5}\\{4}&{3}&{2}\end{array}\right].\nonumber \]

Vamos a comprobar esto. Considera el vector

\[\vec{x}=\left[\begin{array}{c}{1}\\{2}\\{3}\end{array}\right].\nonumber \]

Estrictamente a partir de la definición original, podemos calcular eso

\[T(\vec{x})=T\left(\left[\begin{array}{c}{1}\\{2}\\{3}\end{array}\right]\right)=\left[\begin{array}{c}{1+2}\\{3-3}\\{4+15}\\{4+6+6}\end{array}\right]=\left[\begin{array}{c}{3}\\{0}\\{19}\\{16}\end{array}\right].\nonumber \]

Ahora\(T(\vec{x})\) cómpule por computación\([T]\vec{x}=A\vec{x}\).

\[A\vec{x}=\left[\begin{array}{ccc}{1}&{1}&{0}\\{3}&{0}&{-1}\\{0}&{2}&{5}\\{4}&{3}&{2}\end{array}\right]\left[\begin{array}{c}{1}\\{2}\\{3}\end{array}\right]=\left[\begin{array}{c}{3}\\{0}\\{19}\\{16}\end{array}\right].\nonumber \]

¡Coinciden! \(^{6}\)

Hagamos otro ejemplo, uno que esté más orientado a la aplicación.

Ejemplo\(\PageIndex{4}\)

Un gerente de equipo de beisbol ha recopilado datos básicos sobre sus bateadores. Tiene el número de sencillos, dobles, triples y jonrones que han bateado en el último año. Para cada jugador, quiere dos datos más: el número total de hits y el número total de bases.

Utilizando las técnicas desarrolladas en esta sección, idear un método para que el directivo logre su objetivo.

Solución

Si el manager solo quiere computar esto para unos pocos jugadores, entonces podría hacerlo a mano con bastante facilidad. Después de todo:

\[\text{total # hits = # of singles + # of doubles + # of triples + # of home runs,}\nonumber \]

y

\[\text{total # bases = # of singles + }2\times\text{# of doubles + }3\times\text{# of triples + }4\times\text{# of home runs.}\nonumber \]

No obstante, si tiene muchos jugadores por los que hacer esto, probablemente querría una forma de automatizar el trabajo. Una forma de abordar el problema comienza con reconocer que quiere introducir cuatro números en una función (es decir, el número de sencillos, dobles, etc.) y quiere dos números como salida (es decir, número de hits y bases). Así quiere una transformación\(T\):\(\mathbb{R}^{4}\to\mathbb{R}^{2}\) donde cada vector en\(\mathbb{R}^{4}\) pueda interpretarse como

\[\left[\begin{array}{c}{\text{# of singles}} \\ {\text{# of doubles}} \\ {\text{# of triples}} \\ {\text{# of home runs}}\end{array}\right],\nonumber \]

y cada vector\(\mathbb{R}^{2}\) puede interpretarse como

\[\left[\begin{array}{c}{\text{# of hits}} \\ {\text{# of bases}} \end{array}\right].\nonumber \]

Para encontrar\([T]\), él calcula\(T(\vec{e_{1}})\),\(T(\vec{e_{2}})\),\(T(\vec{e_{3}})\) y\(T(\vec{e_{4}})\).

\[\begin{array}{ccc}{\begin{aligned}T(\vec{e_{1}})&=T\left(\left[\begin{array}{c}{1}\\{0}\\{0}\\{0}\end{array}\right]\right) \\ &=\left[\begin{array}{c}{1}\\{1}\end{array}\right]\end{aligned}}&{\quad}&{\begin{aligned}T(\vec{e_{2}})&=T\left(\left[\begin{array}{c}{0}\\{1}\\{0}\\{0}\end{array}\right]\right) \\ &=\left[\begin{array}{c}{1}\\{2}\end{array}\right]\end{aligned}}\\ {\begin{aligned}T(\vec{e_{3}})&=T\left(\left[\begin{array}{c}{0}\\{0}\\{1}\\{0}\end{array}\right]\right) \\ &=\left[\begin{array}{c}{1}\\{3}\end{array}\right]\end{aligned}}&{\quad}&{\begin{aligned}T(\vec{e_{4}})&=T\left(\left[\begin{array}{c}{0}\\{0}\\{0}\\{1}\end{array}\right]\right) \\ &=\left[\begin{array}{c}{1}\\{4}\end{array}\right]\end{aligned}} \end{array}\nonumber \]

(¿Qué significan estos cálculos? Por ejemplo, encontrar\(T(\vec{e_{3}}) = \left[\begin{array}{c}{1}\\{3}\end{array}\right]\) significa que un triple cuenta como\(1\) hit y\(3\) bases).
Así, nuestra matriz de transformación\([T]\) es

\[[T]=A=\left[\begin{array}{cccc}{1}&{1}&{1}&{1}\\{1}&{2}&{3}&{4}\end{array}\right].\nonumber \]

A modo de ejemplo, consideremos a un jugador que tuvo\(102\) sencillos,\(30\) dobles,\(8\) triples y\(14\) jonrones. Al usar\(A\), encontramos que

\[\left[\begin{array}{cccc}{1}&{1}&{1}&{1}\\{1}&{2}&{3}&{4}\end{array}\right]\left[\begin{array}{c}{102}\\{30}\\{8}\\{14}\end{array}\right]=\left[\begin{array}{c}{154}\\{242}\end{array}\right],\nonumber \]

lo que significa que el jugador tenía\(154\) golpes y bases\(242\) totales.

Una pregunta que debemos hacer respecto al ejemplo anterior es “¿Cómo sabemos que la función que utilizó el gerente era en realidad una transformación lineal? Después de todo, antes estábamos equivocados —el ejemplo de traducción al inicio de esta sección nos había engañado al principio”.

Este es un buen punto; la respuesta es bastante fácil. Recordar de Ejemplo\(\PageIndex{1}\) la transformación

\[T_{98}\left(\left[\begin{array}{c}{x_{1}}\\{x_{2}}\end{array}\right]\right)=\left[\begin{array}{c}{x_{1}^{2}}\\{2x_{1}}\\{x_{1}x_{2}}\end{array}\right]\nonumber \]

y de Ejemplo\(\PageIndex{3}\)

\[T_{100}\left(\left[\begin{array}{c}{x_{1}}\\{x_{2}}\\{x_{3}}\end{array}\right]\right)=\left[\begin{array}{c}{x_{1}+x_{2}}\\{3x_{1}-x_{3}}\\{2x_{2}+5x_{3}}\\{4x_{1}+3x_{2}+2x_{3}}\end{array}\right],\nonumber \]

donde usamos los subíndices\(T\) para recordarnos de qué ejemplo vinieron.

Encontramos que no\(T_{98}\) era una transformación lineal, sino que afirmamos que\(T_{100}\) era (aunque no lo probamos). ¿Qué hizo la diferencia?

Mira las entradas de\(T_{98}(\vec{x})\) y\(T_{100}(\vec{x})\). \(T_{98}\)contiene entradas donde una variable es cuadrada y donde\(2\) las variables se multiplican juntas — éstas\(T_{98}\) impiden ser lineales. Por otro lado, las entradas de\(T_{100}\) son todas de la forma\(a_1x_1 + \cdots + a_nx_n\); es decir, son solo sumas de las variables multiplicadas por coeficientes. \(T\)es lineal si y sólo si las entradas de\(T(\vec{x})\) son de esta forma. (De ahí que las transformaciones lineales se relacionen con ecuaciones lineales, como se define en la Sección 1.1.) Esta idea es importante.

Idea Clave\(\PageIndex{2}\): Conditions on Linear Transformations

Dejar\(T\):\(\mathbb{R}^{n}\to\mathbb{R}^{m}\) ser una transformación y considerar las entradas de

\[T(\vec{x})=T\left(\left[\begin{array}{c}{x_{1}}\\{x_{2}}\\{\vdots}\\{x_{n}}\end{array}\right]\right).\nonumber \]

\(T\)es lineal si y solo si cada entrada de\(T(\vec{x})\) es de la forma\(a_{1}x_{1}+a_{2}x_{2}+\cdots a_{n}x_{n}.\)

Volviendo a nuestro ejemplo de béisbol, el directivo podría haber definido su transformación como

\[T\left(\left[\begin{array}{c}{x_{1}}\\{x_{2}}\\{x_{3}}\\{x_{4}}\end{array}\right]\right)=\left[\begin{array}{c}{x_{1}+x_{2}+x_{3}+x_{4}}\\{x_{1}+2x_{2}+3x_{3}+4x_{4}}\end{array}\right].\nonumber \]

Dado que eso se ajusta al modelo mostrado en Key Idea\(\PageIndex{2}\), la transformación\(T\) es efectivamente lineal y de ahí que podamos encontrar una matriz\([T]\) que la represente.

Practicemos este concepto más a fondo en un ejemplo.

Ejemplo\(\PageIndex{5}\)

Usando Key Idea\(\PageIndex{2}\), determine si cada una de las siguientes transformaciones es lineal o no.

\[T_{1}\left(\left[\begin{array}{c}{x_{1}}\\{x_{2}}\end{array}\right]\right)=\left[\begin{array}{c}{x_{1}+1}\\{x_{2}}\end{array}\right]\qquad T_{2}\left(\left[\begin{array}{c}{x_{1}}\\{x_{2}}\end{array}\right]\right)=\left[\begin{array}{c}{x_{1}/x_{2}}\\{\sqrt{x_{2}}}\end{array}\right] \qquad T_{3}\left(\left[\begin{array}{c}{x_{1}}\\{x_{2}}\end{array}\right]\right)=\left[\begin{array}{c}{\sqrt{7}x_{1}-x_{2}}\\{\pi x_{2}}\end{array}\right]\nonumber \]

Solución

\(T_1\)¡no es lineal! Esto puede ser una sorpresa, pero no se nos permite agregar constantes a las variables. Al pensar en esto, podemos ver que esta transformación está tratando de lograr la traducción que nos inició en esta sección — se suma\(1\) a todos los\(x\) valores y deja los\(y\) valores solos, desplazando todo a la unidad correcta. Sin embargo, esto no es lineal; nuevamente, observe cómo\(\vec{0}\) no se mapea a\(\vec{0}\).

\(T_2\)tampoco es lineal. No podemos dividir variables, ni podemos poner variables dentro de la función raíz cuadrada (entre otras cosas; nuevamente, ver Sección 1.1). Esto significa que el gerente de béisbol no podría usar matrices para calcular un promedio de bateo, que es (número de aciertos)/(número de en bates).

\(T_3\)es lineal. Recordemos eso\(\sqrt{7}\) y\(\pi\) son solo números, solo coeficientes.

Ya hemos mencionado antes que podemos dibujar vectores distintos a los vectores 2D, aunque cuantas más dimensiones se añada, más difícil se llega a entender. En la siguiente sección aprenderemos sobre cómo graficar vectores en 3D —es decir, cómo dibujar en papel o en la pantalla de una computadora un vector 3D.

Notas al pie

[1] Usamos\(T\) en lugar de\(f\) definir esta función para ayudar a diferenciarla de las funciones “regulares”. Las funciones “Normalmente” se definen usando letras minúsculas cuando la entrada es un número; cuando la entrada es un vector, usamos letras mayúsculas.

[2] Recordemos un principio de lógica: para demostrar que algo no funciona, solo necesitamos mostrar un caso donde falla, lo cual hicimos en Ejemplo\(\PageIndex{1}\). Para demostrar que algo siempre funciona, necesitamos demostrar que funciona para todos los casos; simplemente mostrar que funciona para algunos casos no es suficiente. Sin embargo, hacerlo puede ser útil para comprender mejor la situación.

[3] Recordemos que un vector es solo un tipo especial de matriz, por lo que este teorema también se aplica a la multiplicación matriz-vector.

[4] Es decir, ¿aparte de aplicar la definición directamente?

[5] La idea de que las transformaciones lineales “envían de cero a cero” tiene una interesante relación con la terminología. El lector probablemente esté familiarizado con funciones como\(f(x) = 2x+3\) y probablemente se referiría a esto como una “función lineal”. Sin embargo\(f(0) \neq 0\),, así no\(f\) es “lineal” por nuestra nueva definición de lineal. Nosotros erróneamente llamamos\(f\) “lineal” ya que su gráfica produce una línea, aunque debemos tener cuidado de afirmar en su lugar que “la gráfica de\(f\) es una línea”.

[6] Por supuesto que sí. Ese fue todo el punto.