5.6: Complementario - Análisis Matricial de la Fibra Nerviosa Dendrítica Rami

Introducción

En los módulos anteriores sobre sistemas eléctricos estáticos y dinámicos, analizamos fibras nerviosas básicas e hipotéticas de una rama utilizando una metodología de modelado que denominamos el Cuarteto Strang. Quizás te estés preguntando si este método es lo suficientemente fuerte como para manejar la fibra real de nuestras mentes. De hecho, ¿podemos usar nuestras herramientas en un entorno real (Figura\(\PageIndex{1}\))?

Figura\(\PageIndex{1}\): Una Fibra Nerviosa Real. Una neurona piramidal de la región CA3 del hipocampo de una rata, escaneada con un aumento de X (FIX ME).

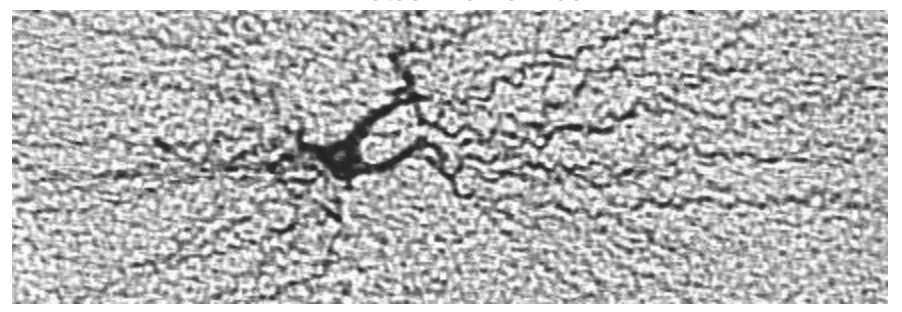
Para responder a tu pregunta, lo anterior es una representación de una neurona del hipocampo de una rata. Las herramientas que hemos refinado nos permitirán modelar las propiedades eléctricas de una dendrita que sale del cuerpo celular de la neurona. Un modelo de tres ramas de tal dendrita, trazado con minuciosa precisión, aparece en la Figura\(\PageIndex{2}\).

Figura\(\PageIndex{2}\): Modelo de Dendríta de 3 ramas. Modelo eléctrico multicompartimental de una fibra dendrita renderizada.

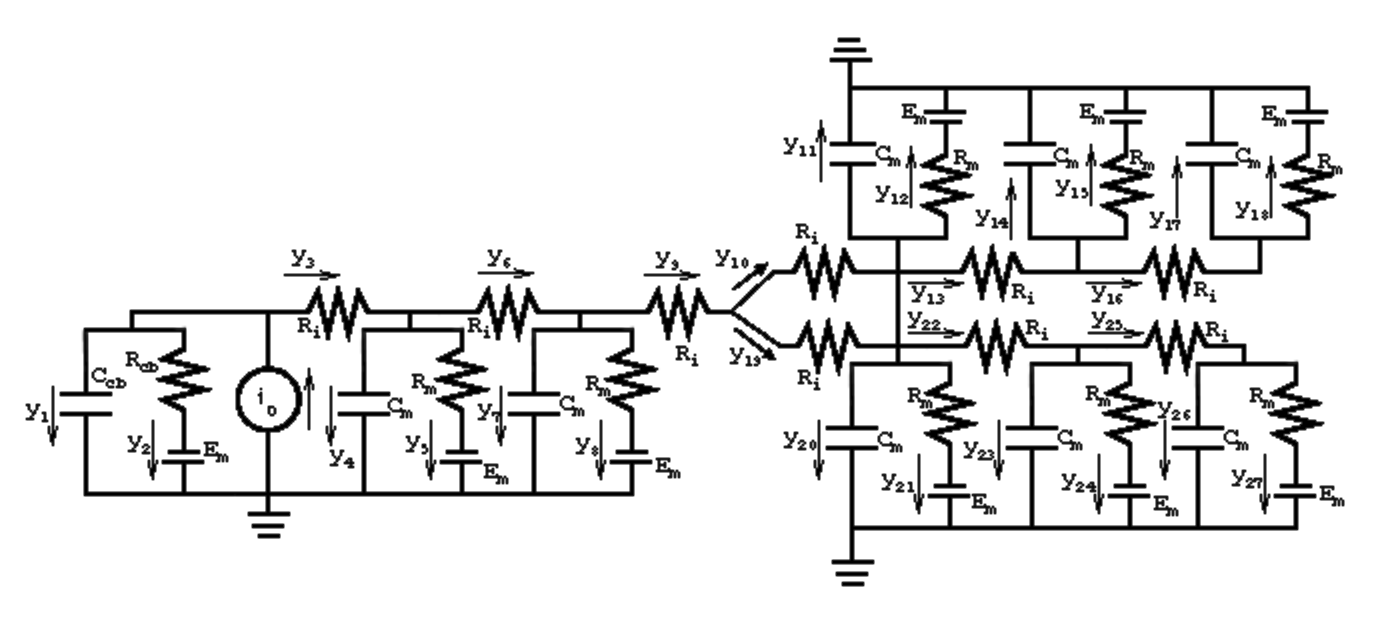
Nuestro modelo multicompartimental revela una estructura de 3 ramas, 10 nodos y 27 bordes a la fibra. Tenga en cuenta que hemos incluido los potenciales de Nernst, el impulso nervioso como fuente de corriente y los bordes adicionales más a la izquierda que representan la corriente de estímulo desviada por el cuerpo celular.

Continuaremos usando nuestra notación anterior, a saber:\(R_{i}\) y\(R_{m}\) denotando cuerpo celular. y resistencias de membrana, respectivamente;\(\textbf{x}\) representando el vector de potenciales\(x_{1} \cdots x_{10}\), y\(\textbf{x}\) denotando el vector de corrientes\(y_{1} \cdots y_{27}\). Usando el valor típico para la membrana de una célula

\[c = 1(μF/cm^{2}) \nonumber\]

derivamos (ver convenciones de variables):

Definición: Capacitancia de un Solo Compartimento

\[C_{m} = 2 \pi a\frac{l}{N}c \nonumber\]

Esta capacitancia se modela en paralelo con la resistencia de la membrana de la célula. Adicionalmente, dejando\(A_{cb}\) denotar el área de superficie del cuerpo celular, recordamos que su capacitancia y resistencia son

Definición: Capacitancia de un Cuerpo Celular

\[C_{cb} = A_{cb} c \nonumber\]

Definición: Resistencia de un Cuerpo Celular

\[C_{cb} = A_{cb} \rho_{m} \nonumber\]

Aplicando el Cuarteto Strang

Paso (S1'): caídas de voltaje

Empecemos a llenar el Cuarteto Strang. Para el Paso (S1'), primero observamos las caídas de voltaje en la figura. Como hay la friolera de 27 de ellos, incluimos solo los seis primeros, que son un poco más de lo que necesitamos para cubrir todas las variaciones en el conjunto:

\[e_{1} = x_{1} \nonumber\]

\[e_{2} = x_{1}-E_{m} \nonumber\]

\[e_{3} = x_{1}-x_{2} \nonumber\]

\[e_{4} = x_{2} \nonumber\]

\[e_{5} = x_{2}-E_{m} \nonumber\]

\[e_{6} = x_{2}-x_{3} \nonumber\]

\[\cdots \nonumber\]

\[e_{27} = x_{10}-E_{m} \nonumber\]

En matriz para, dejando\(\textbf{b}\) denotar el vector de baterías,

\[\begin{array}{ccc} {\textbf{x} = \textbf{b}-A \textbf{x}}&{where}&{\textbf{b} = (-Em) \begin{pmatrix} {0}\\{1}\\{0}\\{0}\\{1}\\{0}\\{0}\\{1}\\{0}\\{0}\\{0}\\{1}\\{0}\\{0}\\{1}\\{0}\\{0}\\{1}\\{0}\\{0}\\{1}\\{0}\\{0}\\{1}\\{0}\\{0}\\{1} \end{pmatrix}} \end{array} \nonumber\]

y

\[A = \begin{pmatrix} {-1}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}\\ {-1}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}\\ {-1}&{1}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}\\{0}&{-1}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}\\ {0}&{-1}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}\\ {0}&{-1}&{1}&{0}&{0}&{0}&{0}&{0}&{0}&{0}\\ {0}&{0}&{-1}&{0}&{0}&{0}&{0}&{0}&{0}&{0}\\ {0}&{0}&{-1}&{0}&{0}&{0}&{0}&{0}&{0}&{0}\\ {0}&{0}&{-1}&{1}&{0}&{0}&{0}&{0}&{0}&{0}\\ {0}&{0}&{0}&{1}&{-1}&{0}&{0}&{0}&{0}&{0}\\ {0}&{0}&{0}&{0}&{-1}&{0}&{0}&{0}&{0}&{0}\\ {0}&{0}&{0}&{0}&{-1}&{0}&{0}&{0}&{0}&{0}\\ {0}&{0}&{0}&{0}&{-1}&{1}&{0}&{0}&{0}&{0}\\ {0}&{0}&{0}&{0}&{0}&{-1}&{0}&{0}&{0}&{0}\\ {0}&{0}&{0}&{0}&{0}&{-1}&{0}&{0}&{0}&{0}\\ {0}&{0}&{0}&{0}&{0}&{-1}&{1}&{0}&{0}&{0}\\ {0}&{0}&{0}&{0}&{0}&{0}&{-1}&{0}&{0}&{0}\\ {0}&{0}&{0}&{0}&{0}&{0}&{-1}&{0}&{0}&{0}\\ {0}&{0}&{0}&{-1}&{0}&{0}&{0}&{1}&{0}&{0}\\ {0}&{0}&{0}&{0}&{0}&{0}&{0}&{-1}&{0}&{0}\\ {0}&{0}&{0}&{0}&{0}&{0}&{0}&{-1}&{0}&{0}\\ {0}&{0}&{0}&{0}&{0}&{0}&{0}&{-1}&{1}&{0}\\ {0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{-1}&{0}\\ {0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{-1}&{0}\\ {0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{-1}&{1}\\ {0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{-1}\\ {0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{-1}\\ \end{pmatrix} \nonumber\]

Aunque nuestra matriz de adyacencia\(A\) es apreciablemente mayor que nuestros ejemplos anteriores, hemos capturado los mismos fenómenos que antes.

Aplicando (S2): Ley de Ohm Aumentada con Ley de Voltaje-Corriente para Capacitores

Ahora, recordando la Ley de Ohm y recordando que la corriente a través de un condensador varía proporcionalmente con la tasa de cambio de tiempo del potencial a través de él, ensamblamos nuestro vector de corrientes. Como antes, enumeramos solo lo suficiente de las 27 corrientes para caracterizar completamente el conjunto:

\[y_{1} = C_{cb} \frac{de_{1}}{dt} \nonumber\]

\[y_{2} = \frac{e_{2}}{R_{cb}} \nonumber\]

\[y_{3} = \frac{e_{3}}{R_{i}} \nonumber\]

\[y_{4} = C_{m} \frac{de_{4}}{dt} \nonumber\]

\[y_{5} = \frac{e_{5}}{R_{m}} \nonumber\]

\[\cdots \nonumber\]

\[y_{27} = \frac{e_{27}}{R_{m}} \nonumber\]

En términos matriciales, esto compila para

\[\textbf{y} = G \textbf{e}+Cd \textbf{e} dt \nonumber\]

donde

Matriz de conductancia

\[G = \begin{pmatrix} {0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}\\ {0}&{\frac{1}{R_{cb}}}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}\\ {0}&{0}&{\frac{1}{R_{i}}}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}\\ {0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}\\ {0}&{0}&{0}&{0}&{\frac{1}{R_{m}}}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}\\ {0}&{0}&{0}&{0}&{0}&{\frac{1}{R_{i}}}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}\\ {0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}\\ {0}&{0}&{0}&{0}&{0}&{0}&{0}&{\frac{1}{R_{i}}}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}\\ {0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{\frac{1}{R_{i}}}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}\\ {0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{\frac{1}{R_{i}}}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}\\ {0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}\\ {0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{\frac{1}{R_{m}}}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}\\ {0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{\frac{1}{R_{i}}}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}\\ {0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}\\ {0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{\frac{1}{R_{m}}}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}\\ {0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{\frac{1}{R_{i}}}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}\\ {0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}\\ {0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{\frac{1}{R_{m}}}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}\\ {0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{\frac{1}{R_{i}}}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}\\ {0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}\\ {0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{\frac{1}{R_{m}}}&{0}&{0}&{0}&{0}&{0}&{0}\\ {0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{\frac{1}{R_{i}}}&{0}&{0}&{0}&{0}&{0}\\ {0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}\\ {0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{\frac{1}{R_{m}}}&{0}&{0}&{0}\\ {0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{\frac{1}{R_{i}}}&{0}&{0}\\ {0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}\\ {0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{\frac{1}{R_{m}}} \end{pmatrix} \nonumber\]

y

Matriz de capacitancia

\[C = \begin{pmatrix} {C_{cb}}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}\\ {0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}\\ {0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}\\ {0}&{0}&{0}&{C_{m}}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}\\ {0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}\\ {0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}\\ {0}&{0}&{0}&{0}&{0}&{0}&{C_{m}}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}\\ {0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}\\ {0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}\\ {0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}\\ {0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{C_{m}}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}\\ {0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}\\ {0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}\\ {0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{C_{m}}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}\\ {0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}\\ {0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}\\ {0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{C_{m}}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}\\ {0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}\\ {0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}\\ {0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{C_{m}}&{0}&{0}&{0}&{0}&{0}&{0}&{0}\\ {0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}\\ {0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}\\ {0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{C_{m}}&{0}&{0}&{0}&{0}\\ {0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}\\ {0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}\\ {0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{C_{m}}&{0}\\ {0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0} \end{pmatrix} \nonumber\]

Paso (S3): Aplicar la Ley de Kirchoff

Nuestro siguiente paso es escribir las ecuaciones para la Ley Actual de Kirchoff. Vemos:

\[i_{0}-y_{1}-y_{2}-y_{3} = 0 \nonumber\]

\[y_{3}-y_{4}-y_{5}-y_{6} = 0 \nonumber\]

\[y_{6}-y_{7}-y_{8}-y_{9} = 0 \nonumber\]

\[y_{9}-y_{10}-y_{19} = 0 \nonumber\]

\[y_{10}-y_{11}-y_{12}-y_{13} = 0 \nonumber\]

\[y_{13}-y_{14}-y_{15}-y_{16} = 0 \nonumber\]

\[y_{16}-y_{17}-y_{18}-y_{19} = 0 \nonumber\]

\[y_{19}-y_{20}-y_{21}-y_{22} = 0 \nonumber\]

\[y_{22}-y_{23}-y_{24}-y_{25} = 0 \nonumber\]

\[y_{25}-y_{26}-y_{27} = 0 \nonumber\]

Como la matriz de\(B\) coeficientes que formaríamos aquí es igual a\(A^{T}\), podemos decir en términos de matriz:

\[A^{T} \textbf{y} = -\textbf{f} \nonumber\]

donde el vector\(\textbf{f}\) está compuesto por\(f_{1} = i_{0}\) y\(f_{2} \cdots 27 = 0\)

Paso (S4): Revolviendo los ingredientes

El paso (S4) nos dirige a ensamblar nuestros trabajos anteriores juntos en una ecuación final, que luego trataremos de resolver. Usando el proceso derivado en el módulo dinámico Strang, llegamos a la ecuación

\[A^{T}CA \frac{d \textbf{x}}{dt}+A^{T}GA \textbf{x} = A^{T}G \textbf{b}+\textbf{f}+A^{T}C \frac{d\textbf{b}}{dt} \nonumber\]

que es la forma general para las ecuaciones de potencial de circuito RC. Como hemos mencionado, esta ecuación presume conocimiento del valor inicial de cada uno de los potenciales,\(\textbf{x}(⁢0) = X\).

Observando nuestro circuito, y dejando\(\frac{1}{R_{foo}} = G_{foo}\), calculamos las cantidades necesarias para rellenar las piezas de Ecuación (para estos cálculos, ver dendrite.m):

\[A^{T}CA = \begin{pmatrix} {C_{cb}}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}\\ {0}&{C_{m}}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}\\ {0}&{0}&{C_{m}}&{0}&{0}&{0}&{0}&{0}&{0}&{0}\\ {0}&{0}&{0}&{C_{m}}&{0}&{0}&{0}&{0}&{0}&{0}\\ {0}&{0}&{0}&{0}&{C_{m}}&{0}&{0}&{0}&{0}&{0}\\ {0}&{0}&{0}&{0}&{0}&{C_{m}}&{0}&{0}&{0}&{0}\\ {0}&{0}&{0}&{0}&{0}&{0}&{C_{m}}&{0}&{0}&{0}\\ {0}&{0}&{0}&{0}&{0}&{0}&{0}&{C_{m}}&{0}&{0}\\ {0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{C_{m}}&{0}\\ {0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{C_{m}} \end{pmatrix} \nonumber\]

\[A^{T}GA = \begin{pmatrix} {G_{i}+G_{cb}}&{-G_{i}}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}\\ {-G_{i}}&{2G_{i}+G_{m}}&{-G_{i}}&{0}&{0}&{0}&{0}&{0}&{0}&{0}\\ {0}&{-G_{i}}&{2G_{i}+G_{m}}&{-G_{i}}&{0}&{0}&{0}&{0}&{0}&{0}\\ {0}&{0}&{-G_{i}}&{3G_{i}}&{-G_{i}}&{0}&{0}&{-G_{i}}&{0}&{0}\\ {0}&{0}&{0}&{-G_{i}}&{2G_{i}+G_{m}}&{-G_{i}}&{0}&{0}&{0}&{0}\\ {0}&{0}&{0}&{0}&{-G_{i}}&{2G_{i}+G_{m}}&{-G_{i}}&{0}&{0}&{0}\\ {0}&{0}&{0}&{0}&{0}&{-G_{i}}&{G_{i}+G_{m}}&{0}&{0}&{0}\\ {0}&{0}&{0}&{-G_{i}}&{0}&{0}&{0}&{2G_{i}+G_{m}}&{-G_{i}}&{0}\\ {0}&{0}&{0}&{0}&{0}&{0}&{0}&{-G_{i}}&{2G_{i}+G_{m}}&{-G_{i}}\\ {0}&{0}&{0}&{0}&{0}&{0}&{0}&{0}&{-G_{i}}&{G_{i}+G_{m}} \end{pmatrix} \nonumber\]

\[A^{T}G \textbf{b} = E_{m} \begin{pmatrix} {G_{cb}}\\ {G_{m}}\\ {G_{m}}\\ {0}\\ {G_{m}}\\ {G_{m}}\\ {G_{m}}\\ {G_{m}}\\ {G_{m}}\\ {G_{m}} \end{pmatrix} \nonumber\]

\[A^{T}C \frac{d \textbf{b}}{dt} = \textbf{0} \nonumber\]

y un potencial inicial (descanso) de

\[\textbf{x}(0) = E_{m} \begin{pmatrix} {1}\\ {1}\\ {1}\\ {1}\\ {1}\\ {1}\\ {1}\\ {1}\\ {1}\\ {1} \end{pmatrix} \nonumber\]

Aplicación del Método Backward-Euler

Dado que nuestro sistema es tan grande, el método Backward-Euler es el mejor camino hacia una solución. Al observar la matriz\(A^{T}CA\) observamos que es singular y por lo tanto no invertible. Esta singularidad surge del nodo que conecta las tres ramas de la fibra y nos impide utilizar la ecuación simple\(\textbf{x}' = B \textbf{x}+\textbf{g}\), que usamos en anteriores uler-ings hacia atrás. Sin embargo, veremos que una modesta generalización a nuestra forma anterior arroja Ecuación:

\[D \textbf{x}' = E\textbf{x}+\textbf{g} \nonumber\]

capturando la forma de nuestro sistema y permitiéndonos resolver para\(\textbf{x}⁢(t)\) Ecuación de la siguiente manera:

\[D \textbf{x}' = E\textbf{x}+\textbf{g} \nonumber\]

\[D \frac{\tilde{x}(t)-\tilde{x}(t-dt)}{dt} = E\tilde{x}(t)+\textbf{g} \nonumber\]

\[(D-Edt) \tilde{x}(t) = D\tilde{x}(t-dt)+\textbf{g}dt \nonumber\]

\[\tilde{x}(t) = (D-Edt)^{-1}(\tilde{x}(t-dt)+\textbf{g}dt) \nonumber\]

donde en nuestro caso

\[D = A^{T}CA \nonumber\]

\[E = -(A^{T}GA) \nonumber\]

\[\textbf{g} = A^{T}G \textbf{b}+\textbf{f} \nonumber\].

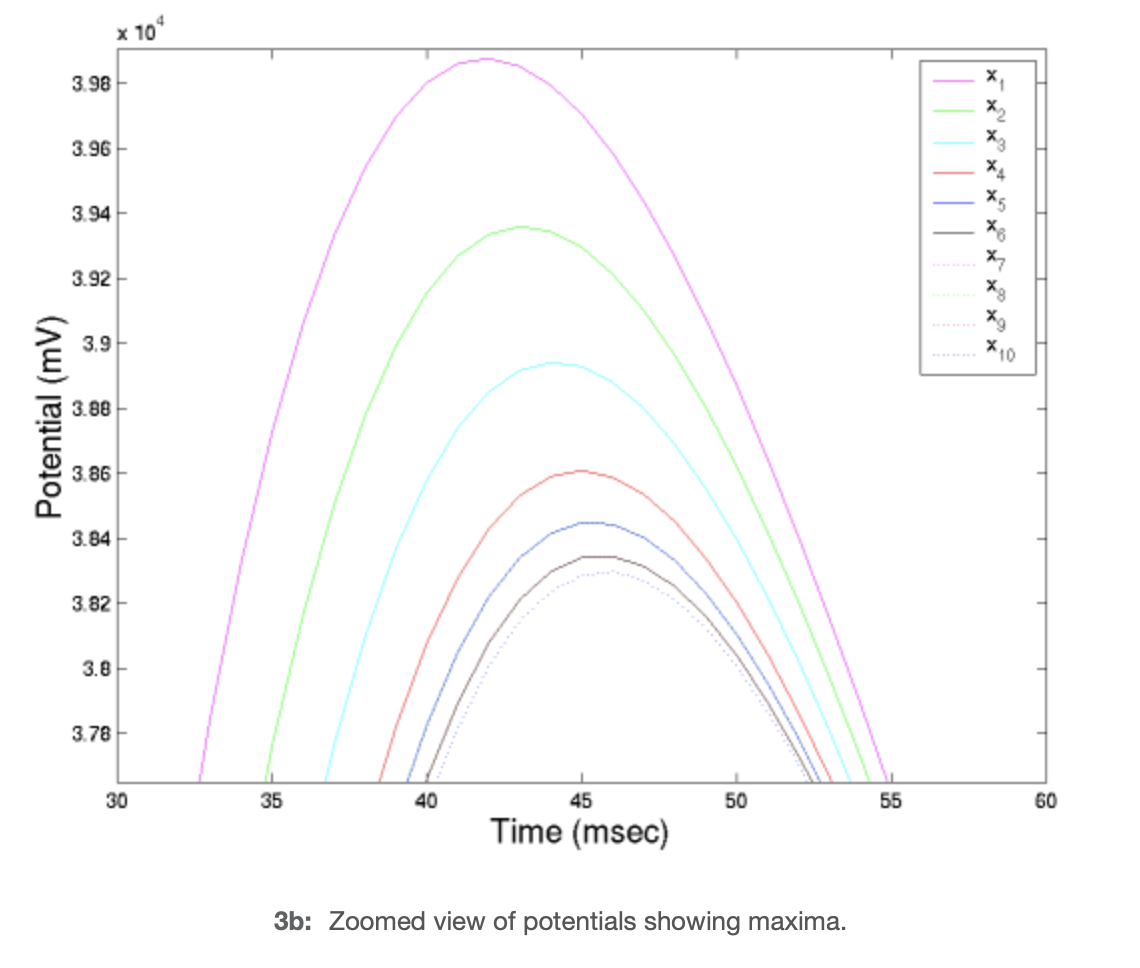
Este método se implementa en dendrite.m con dimensiones celulares típicas y propiedades de resistividad, produciendo la siguiente gráfica de potenciales.

Gráfica de Potenciales de Dendrítas

Figura 3.