8.1: Coordenadas polares y gráficas polares
- Page ID
- 114606
- Entender las coordenadas polares.
- Convertir puntos entre coordenadas cartesianas y polares.
Es probable que haya encontrado el sistema de coordenadas cartesianas en muchos aspectos de las matemáticas. Existe una forma alternativa de representar puntos en el espacio, llamadas coordenadas polares. La idea se sugiere en el siguiente cuadro.
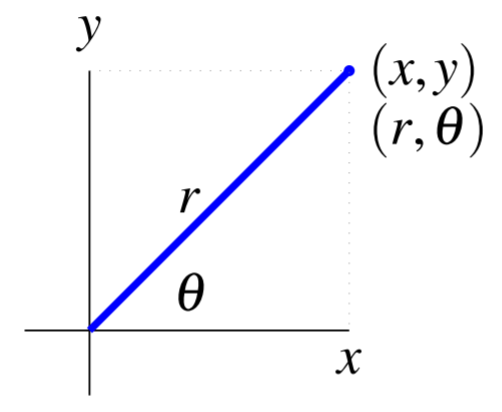
Considera el punto anterior, que se especificaría como\((x,y)\) en las coordenadas cartesianas. También podemos especificar este punto usando coordenadas polares, que escribimos como\(\left( r, \theta \right)\). El número\(r\) es la distancia desde el origen\(\left( 0,0\right)\) hasta el punto, mientras que\(\theta\) es el ángulo que se muestra entre el\(x\) eje positivo y la línea desde el origen hasta el punto. De esta manera, el punto se puede especificar en coordenadas polares como\(\left(r, \theta \right)\).
Ahora supongamos que se nos da un par ordenado\(\left( r,\theta \right)\) donde\(r\) y\(\theta\) son números reales. Queremos determinar el punto especificado por este par ordenado. Podemos utilizar\(\theta\) para identificar un rayo desde el origen de la siguiente manera. Deja que el rayo\(\left( 0,0\right)\) pase desde el punto\(\left( \cos \theta ,\sin \theta \right)\) como se muestra.
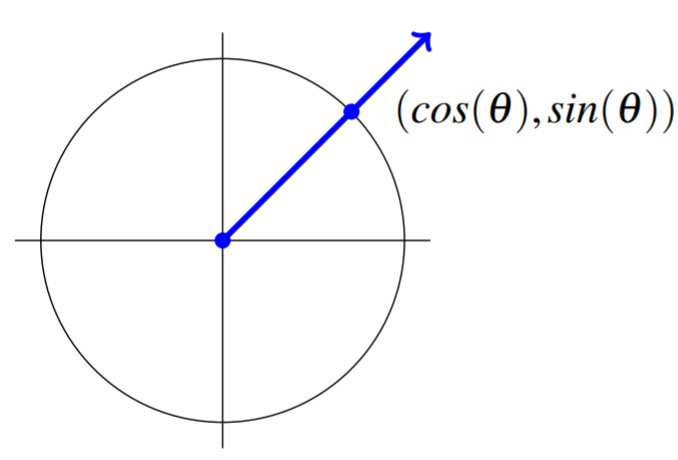
El rayo se identifica en la gráfica como la línea desde el origen, pasando por el punto\((\mbox{cos}(\theta),\mbox{sin}(\theta))\). Ahora si\(r>0,\) ir una distancia igual a\(r\) en la dirección de la flecha mostrada comenzando en\((0,0)\). Si\(r<0,\) se mueven en la dirección opuesta a una distancia de\(\left\vert r\right\vert\). Este es el punto determinado por\(\left( r,\theta \right)\).
Es común suponer que\(\theta\) está en el intervalo\([0,2\pi )\) y\(r>0.\) en este caso, existe una relación muy sencilla entre las coordenadas cartesianas y polares, dada por\[x=r\cos \left( \theta \right) ,\ \ y=r\sin \left( \theta \right) \label{cartpolcoord}\]
Estas ecuaciones demuestran cómo encontrar las coordenadas cartesianas cuando se nos dan las coordenadas polares de un punto. También se pueden utilizar para encontrar las coordenadas polares cuando sepamos\(\left( x, y \right)\). Una forma más sencilla de hacerlo son las siguientes ecuaciones:\[\begin{array}{l} r = \sqrt{x^2 + y^2} \\ \\ \mbox{tan} \left(\theta\right) = \frac{y}{x} \end{array} \label{polcartcoord}\]
En el siguiente ejemplo, observamos cómo encontrar las coordenadas cartesianas de un punto especificado por coordenadas polares.
Las coordenadas polares de un punto en el plano son\(\left( 5,\pi /6\right)\). Encuentra las coordenadas cartesianas de este punto.
Solución
El punto es especificado por las coordenadas polares\(\left( 5,\pi /6\right)\). Por lo tanto\(r=5\) y\(\theta = \pi /6\). De\(\eqref{cartpolcoord}\)\[x= r \cos \left( \theta \right)= 5\cos \left( \frac{\pi }{6}\right) = \frac{5}{2}\sqrt{3}\nonumber \]\[y= r \sin \left( \theta \right) = 5\sin \left( \frac{\pi }{6}\right) = \frac{5}{2}\nonumber \] Así son las coordenadas cartesianas\(\left( \frac{5}{2}\sqrt{3}, \frac{5}{2}\right)\). El punto se muestra en la siguiente gráfica.
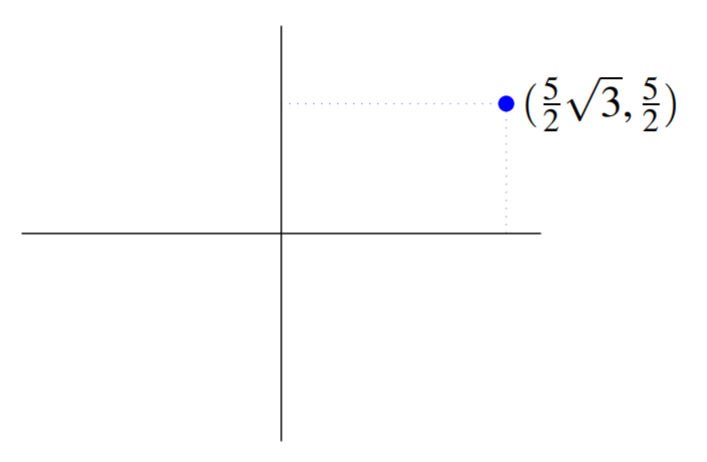
Considera el siguiente ejemplo del caso donde\(r < 0\).
Las coordenadas polares de un punto en el plano son\(\left( -5,\pi /6\right) .\) Encuentra las coordenadas cartesianas.
Solución
Para el punto especificado por las coordenadas polares\(\left( -5, \pi /6 \right)\),\(r=-5\), y\(x\theta = \pi /6\). De\(\eqref{cartpolcoord}\)\[x= r \cos \left( \theta \right)= -5\cos \left( \frac{\pi }{6}\right) = -\frac{5}{2}\sqrt{3}\nonumber \]\[y= r \sin \left( \theta \right) = -5\sin \left( \frac{\pi }{6}\right) = -\frac{5}{2}\nonumber \] Así son las coordenadas cartesianas\(\left( -\frac{5}{2}\sqrt{3}, -\frac{5}{2}\right)\). El punto se muestra en la siguiente gráfica.
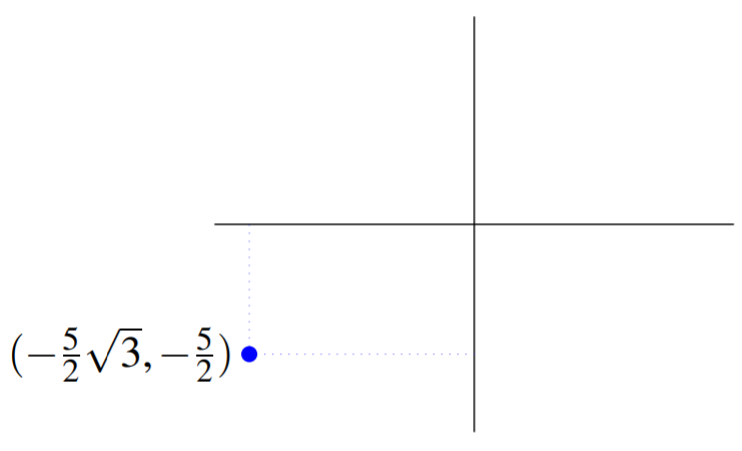
Recordemos del ejemplo anterior que para el punto especificado por\(\left( 5, \pi /6 \right)\), las coordenadas cartesianas son\(\left( \frac{5}{2}\sqrt{3}, \frac{5}{2}\right)\). Observe que en este ejemplo, multiplicando\(r\) por\(-1\), las coordenadas cartesianas resultantes también se multiplican por\(-1\).
El siguiente cuadro exhibe ambos puntos en los dos ejemplos anteriores para enfatizar cómo están justo en lados opuestos\(\left( 0,0\right)\) pero a la misma distancia de\(\left( 0,0\right)\).
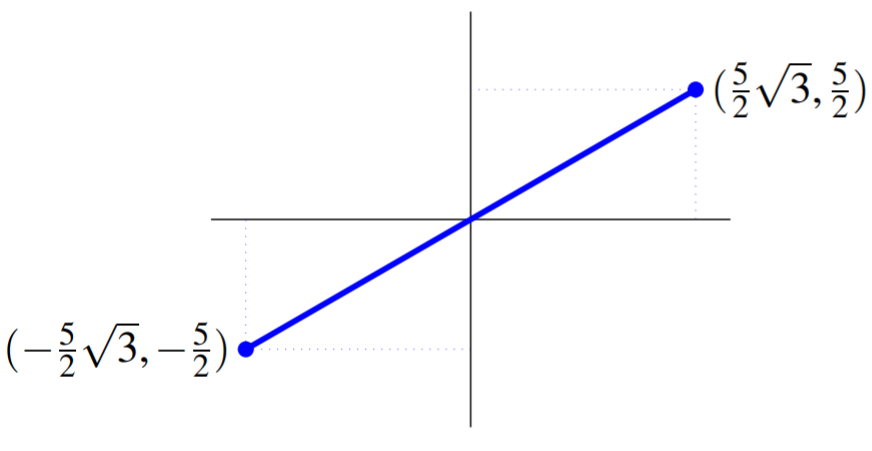
En los siguientes dos ejemplos, observamos cómo convertir coordenadas cartesianas en coordenadas polares.
Supongamos que las coordenadas cartesianas de un punto son\(\left( 3,4\right)\). Encuentra un par de coordenadas polares que correspondan a este punto.
Solución
Usando ecuación\(\eqref{polcartcoord}\), podemos encontrar\(r\) y\(\theta\). De ahí\(r=\sqrt{3^{2}+4^{2}}=5\). Queda por identificar el ángulo\(\theta\) entre el\(x\) eje positivo y la línea desde el origen hasta el punto. Dado que tanto\(x\) los\(y\) valores como son positivos, el punto está en el primer cuadrante. Por lo tanto,\(\theta\) es entre\(0\) y\(\pi /2\ \). Usando esto y\(\eqref{polcartcoord}\), tenemos que resolver:\[\mbox{tan}\left(\theta \right)=\frac{4}{3}\nonumber \] Por el contrario, podemos usar la ecuación de la\(\eqref{cartpolcoord}\) siguiente manera:\[3=5\cos \left( \theta \right)\nonumber \]\[4 = 5\sin \left( \theta \right)\nonumber \] Resolviendo estas ecuaciones, nos encontramos con que, aproximadamente,\(\theta =0.\, 927\,295\) radianes.
Considera el siguiente ejemplo.
Supongamos que las coordenadas cartesianas de un punto son\(\left( -\sqrt{3},1\right)\). Encuentra las coordenadas polares que corresponden a este punto.
Solución
Dado el punto\(\left( -\sqrt{3}, 1\right)\),\[\begin{aligned} r &= \sqrt{ 1^2 + (-\sqrt{3})^2}\\ &= \sqrt{1 + 3}\\ &=2\end{aligned}\] en este caso, el punto está en el segundo cuadrante ya que el\(x\) valor es negativo y el\(y\) valor es positivo. Por lo tanto,\(\theta\) será entre\(\pi/2\) y\(\pi\). Resolviendo las ecuaciones\[-\sqrt{3}= 2 \cos \left(\theta\right)\nonumber \]\[1 = 2 \sin \left( \theta\right)\nonumber \] encontramos que\(\theta = 5\pi /6.\) De ahí las coordenadas polares para este punto son\(\left(2, 5\pi /6 \right)\).
Considera este ejemplo. Supongamos que usamos\(r=-2\) y\(\theta =2\pi -\left( \pi /6\right) = 11\pi /6\). Estas coordenadas especifican el mismo punto que el anterior. Observe que hay infinitamente muchas formas de identificar este punto en particular con coordenadas polares. De hecho, cada punto se puede representar con coordenadas polares de infinitamente muchas formas. Debido a esto, suele ser el caso que\(\theta\) se limita a mentir en algún intervalo de longitud\(2\pi\) y\(r>0\), para números reales\(r\) y\(\theta\).
Al igual que con las coordenadas cartesianas, es posible utilizar las relaciones entre las coordenadas polares para especificar puntos en el plano. El proceso de bosquejar las gráficas de estas relaciones es muy similar al utilizado para bosquejar gráficas de funciones en coordenadas cartesianas. Considerar una relación entre las coordenadas polares de la forma,\(r=f\left( \theta \right)\). Para graficar tal relación, primero haz una tabla de la forma
| \(\theta\) | \(r\) |
|---|---|
| \ (\ theta\) ">\(\theta_1\) | \ (r\) ">\(f(\theta_1)\) |
| \ (\ theta\) ">\(\theta_2\) | \ (r\) ">\(f(\theta_2)\) |
| \ (\ theta\) ">\(\vdots\) | \ (r\) ">\(\vdots\) |
Grafica los puntos resultantes y conéctelos con una curva. La siguiente imagen ilustra cómo iniciar este proceso.
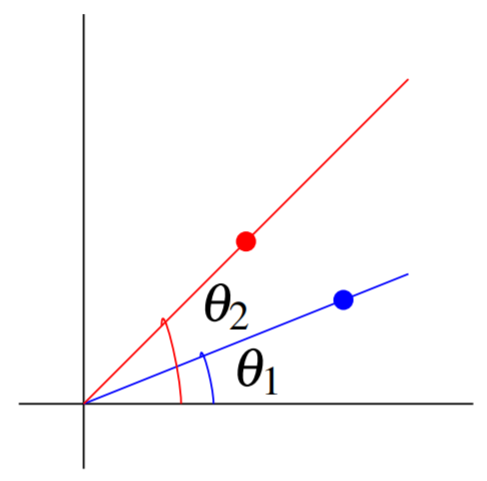
Para encontrar el punto en el plano correspondiente al par ordenado\(\left( f\left( \theta \right) ,\theta \right)\), seguimos el mismo proceso que al encontrar el punto correspondiente a\(\left( r, \theta \right)\).
Consideremos el siguiente ejemplo de este procedimiento, incorporando programas informáticos.
Graficando una Ecuación Polar Grafique la ecuación polar\(r=1+\cos \theta\).
Solución
Utilizaremos el software de computadora Maple para completar este ejemplo. El comando que produce la gráfica polar de la ecuación anterior es:\(>\) plot (1+cos (t), t= 0.. 2*Pi, coords=polar). Aquí usamos\(t\) para representar la variable\(\theta\) por conveniencia. El comando le dice a Maple que\(r\) viene dado por\(1+\cos \left( t\right)\) y eso\(t\in \left[ 0,2\pi \right]\).
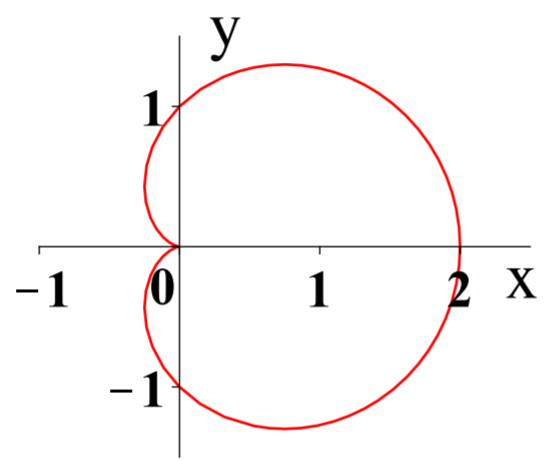
La gráfica anterior tiene sentido cuando se considera en términos de funciones trigonométricas. Supongamos\(\theta =0,r=2\) y vamos\(\theta\) aumentar a\(\pi /2\). A\(\theta\) medida que aumenta,\(\cos \theta\) disminuye a 0. Así, la línea desde el origen hasta el punto de la curva debería acortarse a medida que\(\theta\) va de\(0\) a\(\pi /2\). A medida que\(\theta\) va de\(\pi /2\) a\(\pi\),\(\cos \theta\) disminuye, eventualmente igualando\(-1\) en\(\theta =\pi\). Así\(r=0\) en este punto. Este escenario se representa en la gráfica anterior, que muestra una función llamada cardioide.
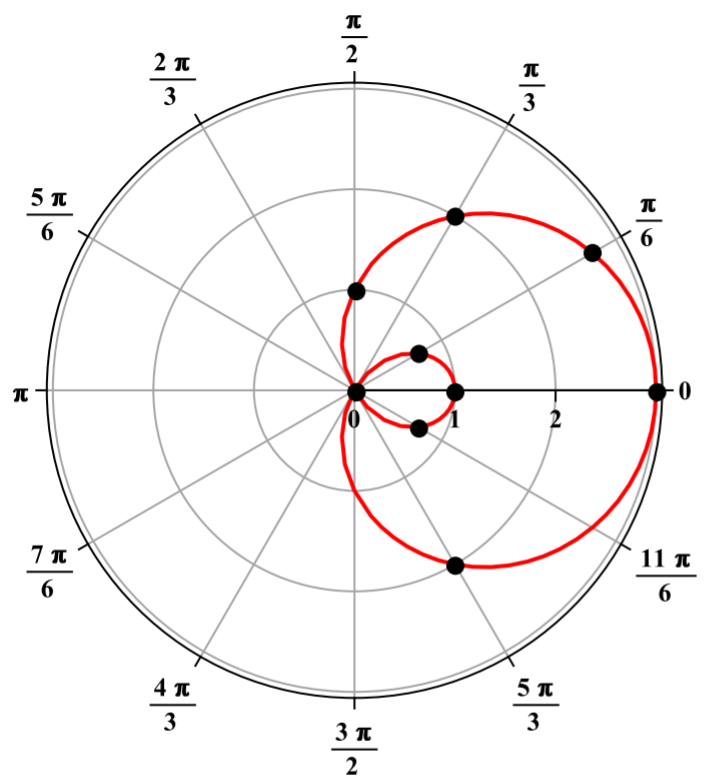
El siguiente cuadro ilustra el procedimiento anterior para obtener la gráfica polar de\(r=1+cos(\theta)\). En esta imagen, los círculos concéntricos corresponden a valores de\(r\) mientras que los rayos del origen corresponden a los ángulos que se muestran en la imagen. El punto en el rayo correspondiente al ángulo\(\pi/6\) se localiza a una\(r = 1+cos(\pi/6)\) distancia del origen. El punto en el rayo correspondiente al ángulo\(\pi/3\) se localiza a una\(r = 1+cos(\pi/3)\) distancia del origen y así sucesivamente. El gráfico polar se obtiene conectando dichos puntos con una curva suave, siendo el resultado la figura que se muestra arriba.
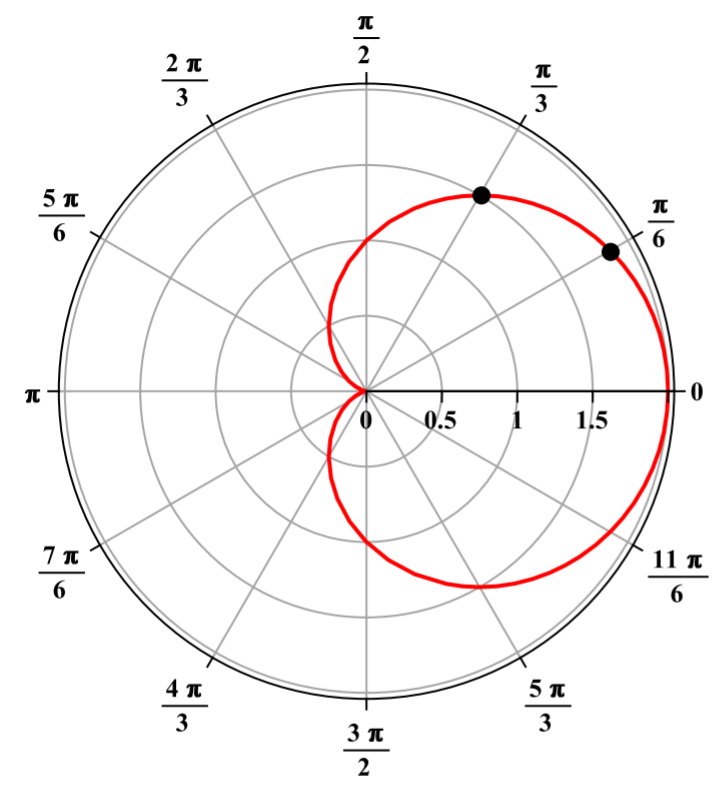
Considera otro ejemplo de construcción de una gráfica polar.
Gráfica\(r=1+2\cos \theta\) para\(\theta \in \left[ 0,2\pi \right]\).
Solución
La gráfica de la ecuación polar\(r=1+2\cos \theta\) para\(\theta \in \left[ 0,2\pi \right]\) se da de la siguiente manera.
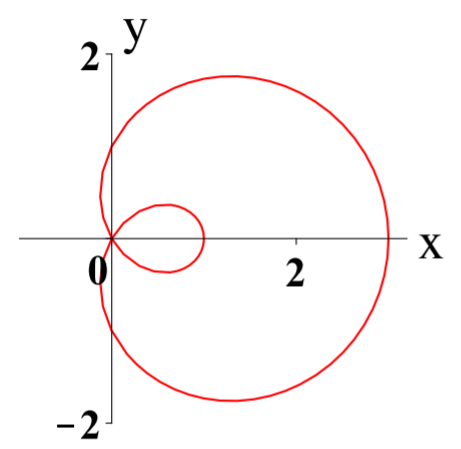
Para ver la forma en que se grafica esto, considera la siguiente imagen. Primero se graficaron los puntos indicados y luego se dibujó la curva para conectar los puntos. Cuando lo hace una computadora, se utilizan muchos más puntos para crear una imagen más precisa.
Considera primero la siguiente tabla de puntos.
| \(\theta\) | \(\pi /6\) | \(\pi /3\) | \(\pi /2\) | \(5\pi /6\) | \(\pi\) | \(4\pi /3\) | \(7\pi /6\) | \(5\pi /3\) |
|---|---|---|---|---|---|---|---|---|
| \(r\) | \(\sqrt{3}+1\) | \(2\) | \(1\) | \(1-\sqrt{3}\) | \(-1\) | \(0\) | \(1-\sqrt{3}\) | \(2\) |
Observe cómo algunas entradas en la tabla tienen\(r<0.\) Para graficar estos puntos, simplemente muévase en dirección opuesta. Este tipo de puntos son responsables del bucle pequeño en el interior del bucle más grande en la gráfica.
El proceso de construcción de estas gráficas puede ser facilitado en gran medida por programas informáticos. Sin embargo, el uso de dicho software no debe reemplazar la comprensión de los pasos involucrados.
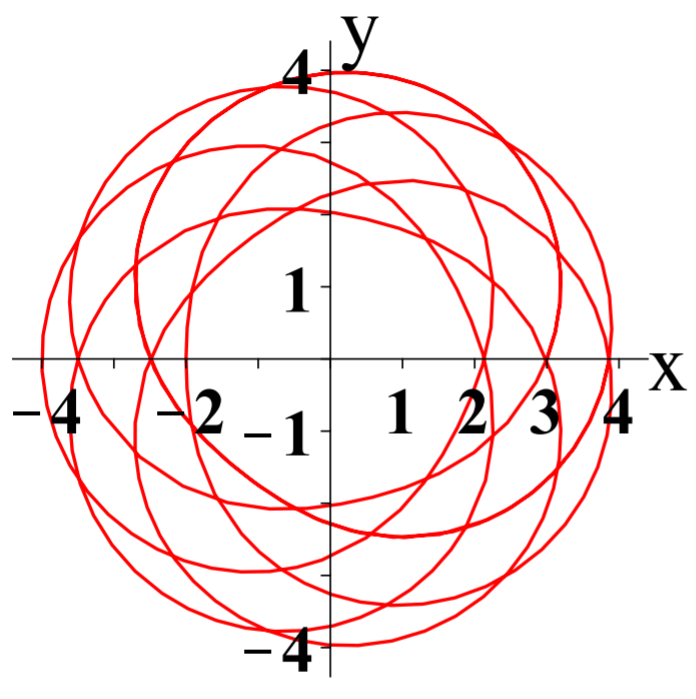
El siguiente ejemplo muestra la gráfica de la ecuación\(r=3+\sin \left( \displaystyle \frac{7\theta }{6}\right)\). For complicated polar graphs, computer software is used to facilitate the process.
Graph \(r=3+\sin \left( \displaystyle \frac{7\theta }{6} \right)\) for \(\theta \in \left[ 0,14\pi \right]\).
Solution
The next example shows another situation in which \(r\) can be negative.
Graph \(r=3sin(4\theta)\) for \(\theta \in \left[ 0,2\pi \right]\).
Solution
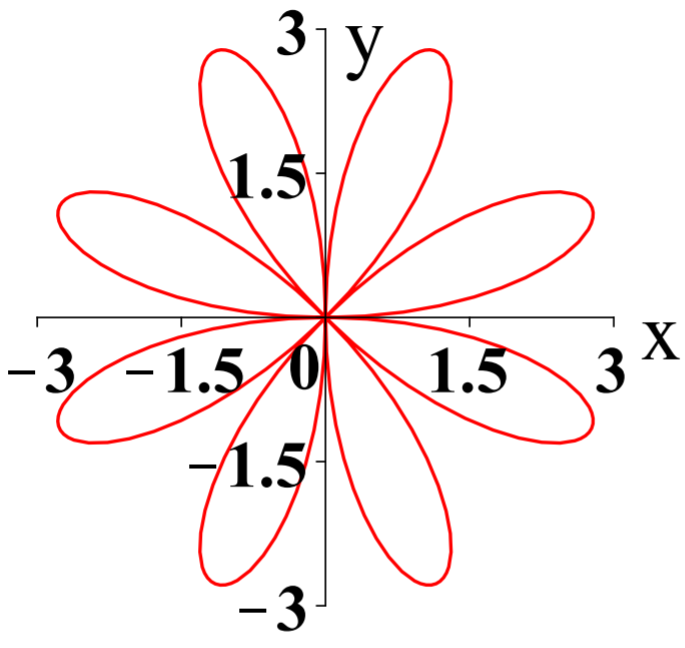
We conclude this section with an interesting graph of a simple polar equation.
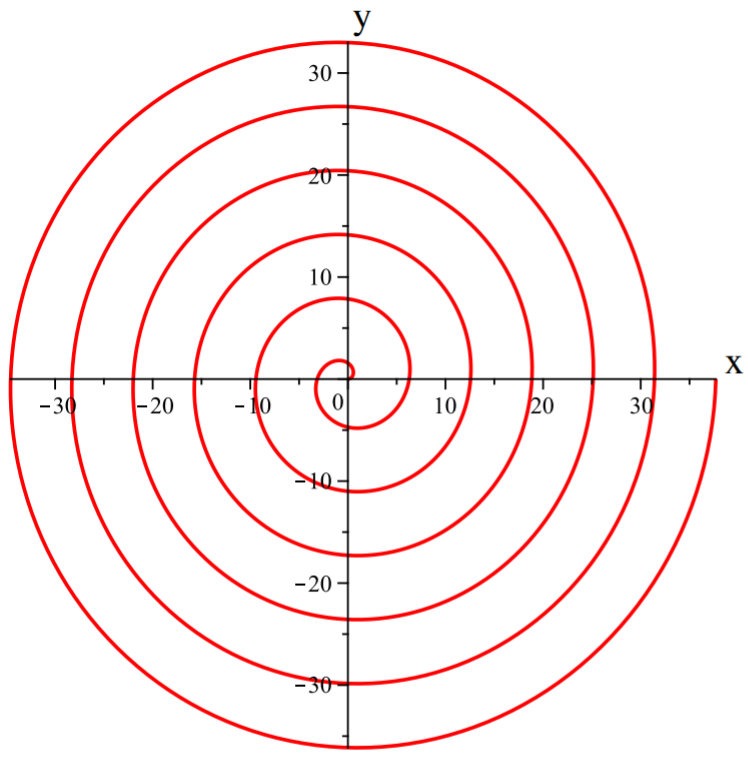
Graph \(r=\theta\) for \(\theta \in [0,2\pi]\).
Solution
The graph of this polar equation is a spiral. This is the case because as \(\theta\) increases, so does \(r\).
In the next section, we will look at two ways of generalizing polar coordinates to three dimensions.


