8.2: Coordenadas esféricas y cilíndricas
- Page ID
- 114605
- Comprender coordenadas cilíndricas y esféricas.
- Convierte puntos entre coordenadas cartesianas, cilíndricas y esféricas.
Las coordenadas esféricas y cilíndricas son dos generalizaciones de coordenadas polares a tres dimensiones. Primero veremos las coordenadas cilíndricas.
Al pasar de coordenadas polares en dos dimensiones a coordenadas cilíndricas en tres dimensiones, usamos las coordenadas polares en el\(xy\) plano y agregamos una\(z\) coordenada. Por esta razón, utilizamos la notación\((r, \theta, z)\) para expresar coordenadas cilíndricas. La relación entre las coordenadas cartesianas\((x,y,z)\) y las coordenadas\((r, \theta, z)\) cilíndricas viene dada por\[\begin{aligned} x& =r\cos \left( \theta \right) \\ y& =r\sin \left( \theta \right) \\ z& =z\end{aligned}\] dónde\(r\geq 0\),\(\theta \in \lbrack 0,2\pi ),\) y\(z\) es simplemente la coordenada cartesiana. Observe que\(x\) y\(y\) se definen como las coordenadas polares habituales en el\(xy\) plano -plano. Recordemos que\(r\) se define como la longitud del rayo desde el origen hasta el punto\((x,y,0)\), mientras que\(\theta\) es el ángulo entre el\(x\) eje positivo y este mismo rayo.
Para ilustrar este sistema de coordenadas, considere las siguientes dos imágenes. En el primero de estos, ambos\(r\) y\(z\) son conocidos. El cilindro corresponde a un valor dado para\(r\). Una manera útil de pensar\(r\) es como la distancia entre un punto en tres dimensiones y el\(z\) eje. Cada punto del cilindro que se muestra está a la misma distancia del\(z\) eje. Dando un valor para\(z\) los resultados en un círculo horizontal, o sección transversal del cilindro a la altura dada en el\(z\) eje (se muestra a continuación como una línea negra en el cilindro). En la segunda imagen, el punto se especifica completamente conociendo también\(\theta\) como se muestra.
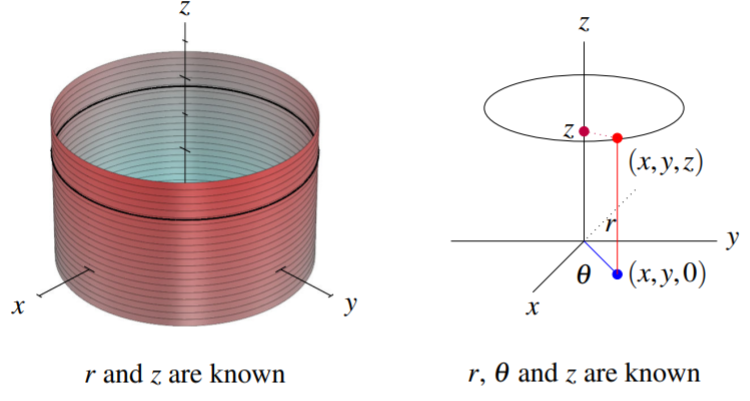
Cada punto del espacio tridimensional que no sea el\(z\) eje tiene coordenadas cilíndricas únicas. Por supuesto que hay infinitamente muchas coordenadas cilíndricas para el origen y para el\(z\) eje -eje. Cualquiera\(\theta\) funcionará si\(r=0\) y\(z\) se da.
Consideremos ahora las coordenadas esféricas, la segunda generalización de la forma polar en tres dimensiones. Para un punto\((x,y,z)\) en el espacio tridimensional, las coordenadas esféricas se definen de la siguiente manera. \[\begin{array}{l} \rho: \mbox{the length of the ray from the origin to the point}\\ \theta: \mbox{the angle between the positive $x$-axis and the ray from the origin to the point $(x,y,0)$}\\ \phi: \mbox{the angle between the positive $z$-axis and the ray from the origin to the point of interest} \end{array}\nonumber \]Las coordenadas esféricas están determinadas por\(\left( \rho ,\phi ,\theta \right)\). La relación entre estas y las coordenadas cartesianas\(\left( x,y,z \right)\) para un punto es la siguiente. \[\begin{aligned} x& =\rho \sin \left( \phi \right) \cos \left( \theta \right) ,\ \phi \in \left[ 0,\pi \right] \\ y& =\rho \sin \left( \phi \right) \sin \left( \theta \right) ,\text{ }\theta \in \lbrack 0,2\pi ) \\ z& =\rho \cos \phi \text{, }\rho \geq 0.\end{aligned}\]
Considera las imágenes a continuación. El primero ilustra la superficie cuando\(\rho\) se conoce, que es una esfera de radio\(\rho\). El segundo cuadro corresponde a conocer ambos\(\rho\) y\(\phi\), lo que da como resultado un círculo alrededor del\(z\) eje -eje. Supongamos que la primera imagen demuestra una gráfica de la Tierra. Entonces el círculo en la segunda imagen correspondería a una latitud particular.
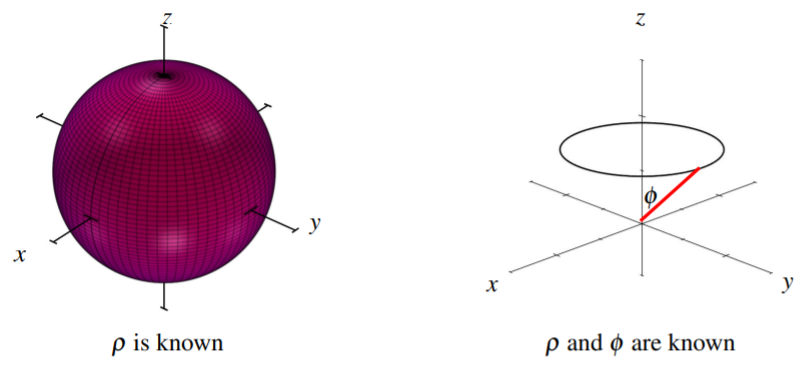
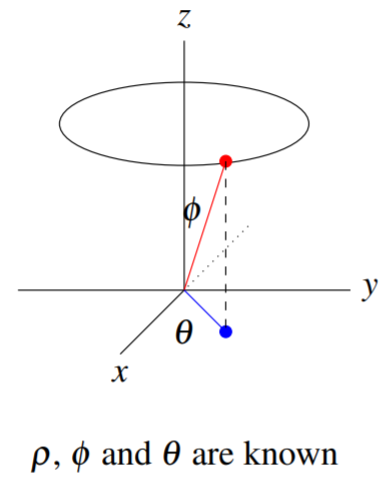
Dando la tercera coordenada, especifica\(\theta\) completamente el punto de interés. Esto se demuestra en el siguiente cuadro. Si la latitud corresponde a\(\phi\), entonces podemos pensar en ella\(\theta\) como la longitud.
La siguiente imagen resume el significado geométrico de los tres sistemas de coordenadas.
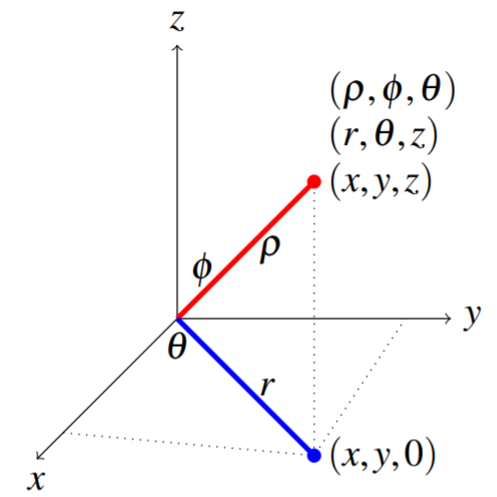
Por lo tanto, podemos representar el mismo punto de tres maneras, usando coordenadas cartesianas\(\left(x,y,z\right)\)\(\left( r, \theta, z \right)\), coordenadas cilíndricas y coordenadas esféricas\(\left( \rho, \phi, \theta \right)\).
Usando esta imagen para revisar, llame al punto de interés\(P\) por conveniencia. Las coordenadas cartesianas para\(P\) son\((x,y,z)\). Entonces\(\rho\) es la distancia entre el origen y el punto\(P\). El ángulo entre el\(z\) eje positivo y la línea entre el origen y\(P\) se denota por\(\phi\). Entonces\(\theta\) es el ángulo entre el\(x\) eje positivo y la línea que une el origen al punto\(\left( x,y,0\right)\) como se muestra. Esto da las coordenadas esféricas,\(( \rho, \phi, \theta)\). Dada la línea desde el origen hasta\(\left( x,y,0\right)\),\(r=\rho \sin(\phi)\) es la longitud de esta línea. Así\(r\) y\(\theta\) determinar un punto en el\(xy\) plano. En otras palabras,\(r\) y\(\theta\) son las coordenadas polares habituales y\(r\geq 0\) y\(\theta \in \lbrack 0,2\pi )\). Dejando\(z\) denotar la\(z\) coordenada habitual de un punto en tres dimensiones,\(\left( r,\theta ,z\right)\) son las coordenadas cilíndricas de\(P\).
La relación entre las coordenadas esféricas y cilíndricas es esa\(r=\rho \sin(\phi)\) y la\(\theta\) es la misma que la\(\theta\) de las coordenadas cilíndricas y polares.
Ahora consideraremos algunos ejemplos.
Expresa la superficie\(z=\frac{1}{\sqrt{3}}\sqrt{x^{2}+y^{2}}\) en coordenadas esféricas.
Solución
Usaremos las ecuaciones de arriba:\[\begin{array}{l} x =\rho \sin \left( \phi \right) \cos \left( \theta \right), \phi \in \left[ 0,\pi \right]\\ y =\rho \sin \left( \phi \right) \sin \left( \theta \right) ,\text{ }\theta \in \lbrack 0,2\pi ) \\ z =\rho \cos \phi \text{, }\rho \geq 0 \end{array} \nonumber\]
Para expresar la superficie en coordenadas esféricas, sustituimos estas expresiones en la ecuación. Esto se hace de la siguiente manera:
\[\rho \cos \left( \phi \right) =\frac{1}{\sqrt{3}}\sqrt{\left( \rho \sin \left( \phi \right) \cos \left( \theta \right) \right) ^{2}+\left( \rho \sin \left( \phi \right) \sin \left( \theta \right) \right) ^{2}}= \frac{1}{3}\sqrt{3}\rho \sin \left( \phi \right). \nonumber\]
Esto se reduce a\[\tan \left( \phi \right)=\sqrt{3} \nonumber\] y así\(\phi =\pi /3\).
Expresar la superficie\(y=x\) en términos de coordenadas esféricas.
Solución
Usando el mismo procedimiento que el ejemplo anterior, esto dice\( \rho \sin \left( \phi \right) \sin \left( \theta \right) =\rho \sin \left( \phi \right) \cos \left( \theta \right)\). Simplificando,\(\sin \left( \theta \right) =\cos \left( \theta \right)\), que también podrías escribir\(\tan \left( \theta \right)=1\).
Concluimos esta sección con un ejemplo de cómo describir una superficie usando coordenadas cilíndricas.
Exprese la superficie\(x^{2}+y^{2}=4\) en coordenadas cilíndricas.
Solución
Recordemos que para convertir de coordenadas cartesianas a cilíndricas, podemos usar las siguientes ecuaciones:\[x =r\cos \left( \theta \right) , y=r\sin \left( \theta \right) , z =z\nonumber \]
Sustituyendo estas ecuaciones en for\(x,y,z\) en la ecuación para la superficie, tenemos\[r^{2}\cos ^{2} \left( \theta \right) +r^{2}\sin ^{2} \left( \theta \right)=4\nonumber \] Esto se puede escribir como\(r^2 ( \cos^{2} \left( \theta \right)+ \sin^{2} \left(\theta\right) ) = 4\). Recordemos eso\(\cos^{2} \left( \theta \right)+ \sin^{2} \left( \theta \right)=1\). Así\(r^{2} = 4\) o\(r=2\).


