4.3: ALGUNAS APLICACIONES DEL TEorema del valor medio
- Page ID
- 107813
En esta sección, asumimos que\(a,b \in \mathbb{R}\) y\(a < b\). En la proposición a continuación, mostramos que es posible utilizar la derivada para determinar si una función es constante. La prueba se basa en el Teorema del Valor Medio.
Dejar\(f\) ser continuo\([a,b]\) y diferenciable en\((a,b)\). Si\(f^{\prime}(x)=0\) por todos\(x \in (a,b)\), entonces\(f\) es constante encendido\([a,b]\).
- Prueba
-
Supongamos por contradicción que no\(f\) es constante en\([a,b]\). Entonces existen\(a_{1}\) y\(b_{1}\) tal que\(a \leq a_{1}<b_{1} \leq b\) y\(f\left(a_{1}\right) \neq f\left(b_{1}\right)\). Por Teorema 4.2.3, existen\(c \in \left(a_{1}, b_{1}\right)\) tales que
\[f^{\prime}(c)=\frac{f\left(b_{1}\right)-f\left(a_{1}\right)}{b_{1}-a_{1}} \neq 0,\]
lo cual es una contradicción. \(\square\)
La siguiente aplicación del Teorema del Valor Medio se refiere al desarrollo de criterios simples para la monotonicidad de funciones de valor real basadas en la derivada.
Dejemos\(f\) ser diferenciables en\((a,b)\).
- Si\(f^{\prime}(x)>0\) por todos\(x \in (a,b)\), entonces\(f\) está aumentando estrictamente en\((a,b)\).
- Si\(f^{\prime}(x)<0\) para todos\(x \in (a,b)\), entonces\(f\) es estrictamente decreciente en\((a,b)\).
- Prueba
-
Demostremos (i). Arreglar cualquiera\(x_{1}, x_{2} \in(a, b)\) con\(x_{1}<x_{2}\). Por Teorema 4.2.3, existe\(c \in \left(x_{1}, x_{2}\right)\) tal que
\[\frac{f\left(x_{2}\right)-f\left(x_{1}\right)}{x_{2}-x_{1}}=f^{\prime}(c)>0.\]
Esto implica\(f\left(x_{1}\right)<f\left(x_{2}\right)\). Por lo tanto,\(f\) está aumentando estrictamente en\((a,b)\). La prueba de (ii) es similar. \(\square\)
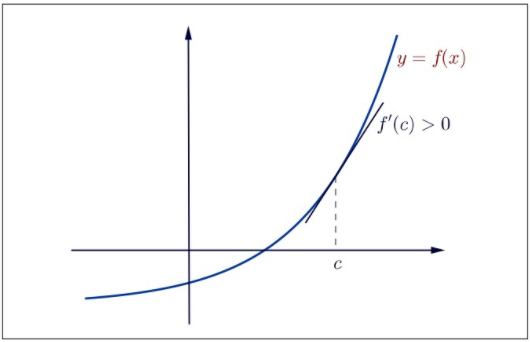
Figura\(4.5\): Función Estrictamente Aumentando.
Dejar\(n \in \mathbb{N}\) y\(f:[0, \infty) \rightarrow \mathbb{R}\) ser dado por\(f(x)=x^{n}\).
Solución
Entonces\(f^{\prime}(x)=n x^{n-1}\). Por lo tanto,\(f^{\prime}(x) > 0\) para todos\(x > 0\) y, así,\(f\) es estrictamente creciente. En particular, esto demuestra que cada número real positivo tiene exactamente una\(n\) -ésima raíz (consulte el Ejemplo 3.4.2).
Supongamos que\(f\) es diferenciable sobre\(I = (a,b)\) y\(f^{\prime}(x) \neq 0\) para todos\(x \in (a,b)\). Entonces\(f\) es uno a uno,\(f(I)\) es un intervalo abierto, y la función inversa\(f^{-1}: f(I) \rightarrow I\) es diferenciable. Por otra parte,
\[\left(f^{-1}\right)^{\prime}(y)=\frac{1}{f^{\prime}(x)},\]
donde\(f(x) = y\).
- Prueba
-
Del Teorema 4.2.5 se deduce que
\[f^{\prime}(x)>0 \text { for all } x \in (a,b), \text { or } f^{\prime}(x)<0 \text { for all } x \in (a,b).\]
Supongamos\(f^{\prime}(x)>0\) para todos\(x \in (a,b)\). Entonces\(f\) está aumentando estrictamente en este intervalo y, de ahí, es uno a uno. Se deduce del Teorema 3.4.10 y la observación 3.4.11 que\(f(I)\) es un intervalo abierto y\(f^{-1}\) es continuo en\(f(I)\).
Queda por demostrar la diferenciabilidad de la función inversa\(f^{-1}\) y la representación de su derivada (4.7). Arreglar cualquiera\(\bar{y} \in f(I)\) con\(\bar{y} = f(\bar{x})\). Vamos\(g=f^{-1}\). Demostraremos que
\[\lim _{y \rightarrow \bar{y}} \frac{g(y)-g(\bar{y})}{y-\bar{y}}=\frac{1}{f^{\prime}(\bar{x})}.\]
Fijar cualquier secuencia\(\left\{y_{k}\right\}\) en\(f(I)\) que converja hacia\(\bar{y}\) y\(y_{k} \neq \bar{y}\) para cada\(k\). Para cada uno\(y_{k}\), existe\(x_{k} \in I\) tal que\(f\left(x_{k}\right)=y_{k}\). Es decir,\(g\left(y_{k}\right)=x_{k}\) para todos\(k\). Se desprende de la continuidad de\(g\) que\(\left\{x_{k}\right\}\) converge a\(\bar{x}\). Entonces
\ [\ comenzar {alineado}
\ lim _ {k\ fila derecha\ infty}\ frac {g\ izquierda (y_ {k}\ derecha) -g (\ bar {y})} {y_ {k} -\ bar {y}} &=\ lim _ {k\ fila derecha\ infty}\ frac {x_ {k} -\ bar {x}} {f izquierda\ (x_ {k}\ derecha) -f (\ bar {x})}\\
&=\ lim _ {k\ fila derecha\ infty}\ frac {1} {\ frac {f\ izquierda (x_ {k}\ derecha) -f (\ bar {x})} {x_ { k} -\ bar {x}}} =\ frac {1} {f^ {\ prime} (\ bar {x})}
\ final {alineado}.\]La prueba ya está completa. \(\square\)
Dejar\(n \in \mathbb{N}\) y considerar la función\(f:(0, \infty) \rightarrow \mathbb{R}\) dada por\(f(x)=x^{n}\).
Solución
Entonces\(f\) es diferenciable y\(f^{\prime}(x)=n x^{n-1} \neq 0\) para todos\(x \in(0, \infty)\). También es claro que\(f((0, \infty))=(0, \infty)\). Se desprende del Teorema de la Función Inversa que\(f^{-1}:(0, \infty) \rightarrow(0, \infty)\) es diferenciable y dado\(y \in(0, \infty)\)
\[\left(f^{-1}\right)^{\prime}(y)=\frac{1}{f^{\prime}\left(f^{-1}(y)\right)}=\frac{1}{n\left(f^{-1}(y)\right)^{n-1}}.\]
Dado\(y > 0\), el valor\(f^{-1}(y)\) es el número real positivo único cuya\(n\) -ésima potencia es\(y\). Llamamos a\(f^{-1}(y)\) la raíz (positiva)\(n\) -ésima de\(y\) y la denotamos por\(\sqrt[n]{y}\). También obtenemos la fórmula
\[\left(f^{-1}\right)^{\prime}(y)=\frac{1}{n(\sqrt[n]{y})^{n-1}}.\]
Ejercicio\(\PageIndex{1}\)
- Dejemos\(f: \mathbb{R} \rightarrow \mathbb{R}\) ser diferenciables. Demostrar que si\(f^{\prime}(x)\) está acotado, entonces\(f\) es Lipschitz continuo y, en particular, uniformemente continuo.
- Dar un ejemplo de una función\(f:(0, \infty) \rightarrow \mathbb{R}\) que sea diferenciable y uniformemente continua pero tal que no\(f^{\prime}(x)\) esté acotada.
- Contestar
-
Agrega textos aquí. No elimine primero este texto.
Ejercicio\(\PageIndex{2}\)
Vamos\(f: \mathbb{R} \rightarrow \mathbb{R}\). Supongamos que existen\(\ell \geq 0\) y\(\alpha > 0\) tal que
\[|f(u)-f(v)| \leq \ell|u-v|^{\alpha} \text { for all } u, v \in \mathbb{R}\].
- Demostrar que\(f\) es uniformemente continuo en\(\mathbb{R}\).
- Demostrar que si\(\alpha > 1\), entonces\(f\) es una función constante.
- Encuentra una función no diferenciable que satisfaga la condición anterior para\(\alpha = 1\).
- Contestar
-
Agrega textos aquí. No elimine primero este texto.
Ejercicio\(\PageIndex{3}\)
Dejar\(f\) y\(g\) ser funciones diferenciables sobre\(\mathbb{R}\) tal que\(f\left(x_{0}\right)=g\left(x_{0}\right)\) y
\[f^{\prime}(x) \leq g^{\prime}(x) \text { for all } x \geq x_{0}.\]
Demostrar que
\[f(x) \leq g(x) \text { for all } x \geq x_{0}.\]
- Contestar
-
Agrega textos aquí. No elimine primero este texto.
Ejercicio\(\PageIndex{4}\)
Dejar que\(f, g: \mathbb{R} \rightarrow \mathbb{R}\) sean funciones diferenciables satisfactorias
- \(f(0)=g(0)=1\)
- \(f(x)>0, g(x)>0\)y\(\frac{f^{\prime}(x)}{f(x)}>\frac{g^{\prime}(x)}{g(x)}\) para todos\(x\).
Demostrar que
\[\frac{f(1)}{g(1)}>1>\frac{g(1)}{f(1)}.\]
- Contestar
-
Agrega textos aquí. No elimine primero este texto.
Ejercicio\(\PageIndex{5}\)
Dejar\(f\) ser dos veces diferenciable en un intervalo abierto\(I\). Supongamos que existen\(a,b,c \in I\) con\(a < b < c\) tal que\(f(a)<f(b)\) y\(f(b)>f(c)\). Demostrar que existen\(d \in(a, c)\) tal que\(f^{\prime \prime}(d)<0\).
- Contestar
-
Agrega textos aquí. No elimine primero este texto.
Ejercicio\(\PageIndex{6}\)
Demostrar que la función\(f\) definida en el Ejercicio 4.1.11 no es monótona en ningún intervalo abierto que contenga\(0\).
- Contestar
-
Agrega textos aquí. No elimine primero este texto.