5.4: CAPÍTULO 4

Ejercicio\(4.1.10\).

Contestar

Usar la identidad\[\lim _{n \rightarrow \infty}\left(\frac{f\left(a+\frac{1}{n}\right)}{f(a)}\right)^{n}=\lim _{n \rightarrow \infty} \exp \left(n\left[\ln \left(f\left(a+\frac{1}{n}\right)\right)-\ln (f(a)]\right)\right. .\]

Ejercicio\(4.1.11\).

Contestar

1. Usando la diferenciabilidad de\(\sin x\) y Teorema 4.1.3, concluimos que la función es diferenciable en cualquiera\(a \neq 0\). Entonces, solo necesitamos mostrar la diferenciabilidad de la función en\(a = 0\) Por la definición de la derivada, considerar el límite\[\lim _{x \rightarrow a} \frac{f(x)-f(a)}{x-a}=\lim _{x \rightarrow 0} \frac{x^{2} \sin (1 / x)+c x}{x}=\lim _{x \rightarrow 0}[x \sin (1 / x)+c] .\] Para cualquiera\(x \neq 0\), tenemos lo\[|x \sin (1 / x)|=|x||\sin (1 / x)| \leq|x| ,\] que implica\[-|x| \leq x \sin (1 / x) \leq|x| .\] Desde\(\lim _{x \rightarrow 0}(-|x|)=\lim _{x \rightarrow 0}|x|=0\), aplicar el teorema squeeze rinde Ahora\[\lim _{x \rightarrow 0} x \sin (1 / x)=0 .\] se deduce que\[f^{\prime}(0)=\lim _{x \rightarrow a} \frac{f(x)-f(a)}{x-a}=\lim _{x \rightarrow 0}[x \sin (1 / x)+c]=c .\] Usando el Teorema 4.1.3 y el hecho de que\(\cos x\) es la derivada de\(\sin x\), la derivada de\(f\) puede escribirse explícitamente como\ [f^ {\ prime} (x) =\ left\ {\ begin {array} {ll}
   2 x\ sin\ frac {1} {x} -\ cos (1/x) +c, &\ text {if} x\ neq 0\ text {;}\\
   c, &\ texto {si} x=0\ texto {.}
   \ end {array}\ derecho.\]

Desde la solución, es importante ver que la conclusión sigue siendo válida si reemplazamos la función\(f\) por\ [g (x) =\ left\ {\ begin {array} {ll}
x^ {n}\ sin\ frac {1} {x}, &\ text {if} x\ neq 0\ text {;}\\
0, &\ text {if} x=0\ text {.}
\ end {array}\ right.\] donde\(n \geq 2\),\(n \in \mathbb{N}\). Tenga en cuenta que la función\(h(x) = cx\) no juega ningún papel en la diferenciabilidad de\(f\).

Podemos generalizar este problema de la siguiente manera. Dejar\(\varphi\) ser una función acotada on\(\mathbb{R}\), es decir, hay\(M > 0\) tal que\[|\varphi(x)| \leq M \text { for all } x \in \mathbb{R} .\] Definir la función\ [f (x) =\ left\ {\ begin {array} {ll}
x^ {n}\ varphi (1/x), &\ text {if} x\ neq 0\ text {;}\\
0, &\ text {if} x=0\ text {,}
\ end {array}\ derecha.\] donde\(n \geq 2\),\(n \in \mathbb{N}\). Entonces\(f\) es diferenciable en\(a = 0\).

Problemas similares:

1. Mostrar que las siguientes funciones son diferenciables en\(\mathbb{R}\):\ [f (x) =\ left\ {\ begin {array} {ll}
   x^ {3/2}\ cos (1/x), &\ text {if} x\ geq 0\ text {;}\\
   0, &\ text {if} x<0
   \ end {array}\ right.\] y\ [f (x) =\ left\ {\ begin {array} {ll}
   x^ {2} e^ {-1/x^ {2}}, &\ text {si} x\ neq 0\ texto {;}\\
   0, &\ texto {si} x=0\ texto {.}
   \ end {array}\ derecho.\]
2. Supongamos que\(\varphi\) es acotado y diferenciable en\(\mathbb{R}\). Definir la función\ [f (x) =\ left\ {\ begin {array} {ll}
   x^ {2} e^ {-1/x^ {2}}, &\ text {if} x\ neq 0\ text {;}\\
   0, &\ text {if} x=0\ text {.}
   \ end {array}\ right.\] Mostrar que si\(n \geq 2\), la función es diferenciable\(\mathbb{R}\) y encuentra su derivada. Demostrar que si\(n = 1\) y\(\lim _{x \rightarrow \infty} \varphi(x)\) no existe, entonces no\(f\) es diferenciable en\(0\).

2. Pista: Observe que\[\lim _{x \rightarrow \infty} \varphi(x) .\]

Ejercicio\(4.2.1\).

Contestar

Definir la función\[h(x) = f(x) - g(x).\] Entonces\(h\) tiene un máximo absoluto en\(x_{0}\). Así,\[h^{\prime}\left(x_{0}\right)=f^{\prime}\left(x_{0}\right)-g^{\prime}\left(x_{0}\right)=0 ,\] lo que implica\(f^{\prime}\left(x_{0}\right)=g^{\prime}\left(x_{0}\right)\).

Ejercicio\(4.2.3\).

Contestar

La desigualdad sostiene obviamente si\(a = b\). En el caso donde\(a \neq b\), la igualdad se puede reescribir como\[\left|\frac{\sin (b)-\sin (a)}{b-a}\right| \leq 1 .\] El cociente\(\left|\frac{\sin (b)-\sin (a)}{b-a}\right|\) es la pendiente de la línea que conecta\((a, f(a))\) y\((b, f(b))\). Tenemos que demostrar que el valor absoluto de la pendiente siempre está sorteado por\(1\), lo que también se puede ver a partir de la figura. El cociente también nos recuerda la aplicación del Teorema del Valor Medio para la función\(f(x) = \sin (x)\).

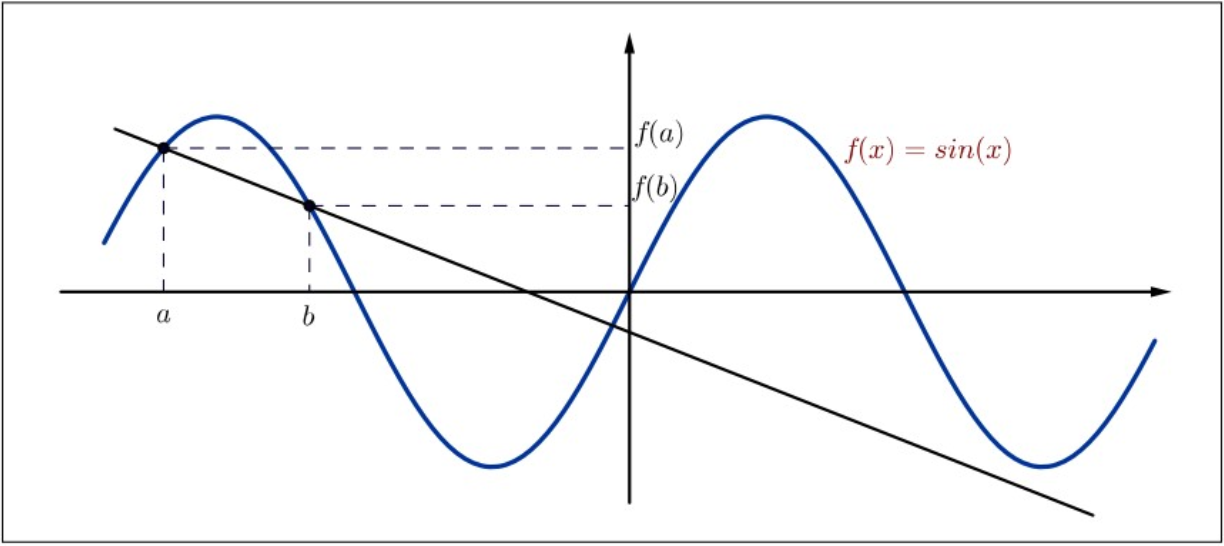
Figura\(5.1\): La función\(f(x) = \sin (x)\).

Considerar el caso donde\(a < b\) y definir la función\(f:[a, b] \rightarrow \mathbb{R}\) por\(f(x) = \sin (x)\). Claramente, la función satisface todos los supuestos del Teorema del Valor Medio en este intervalo con\(f^{\prime}(x)=\cos (x)\) para todos\(x \in (a, b)\).

Por el Teorema del Valor Medio, existe\(c \in (a, b)\) tal aquello\[\frac{f(b)-f(a)}{b-a}=f^{\prime}(c)=\cos (c) ,\] que implica De\[\left|\frac{f(b)-f(a)}{b-a}\right|=|\cos (c)| \leq 1 .\] ello se deduce\(|f(a)-f(b)| \leq|a-b|\). La solución es similar para el caso donde\(a > b\).

Es fundamental darse cuenta de que la propiedad más importante que se requiere para resolver este problema es la amplitud de la derivada de la función. Así, es posible resolver los siguientes problemas con una estrategia similar.

1. \(|\cos (a)-\cos (b)| \leq|a-b|\)Demuéstralo para todos\(a, b \in \mathbb{R}\).
2. \(\left|\ln \left(1+e^{2 a}\right)-\ln \left(1+e^{2 b}\right)\right| \leq 2|a-b|\)Demuéstralo para todos\(a, b \in \mathbb{R}\).

Ejercicio\(4.2.4\).

Contestar

\[f(x)=x+\sum_{k=1}^{n}\left(a_{k} \sin k x+b_{k} \cos k x\right) .\]Definamos\(f:[-\pi, \pi] \rightarrow \mathbb{R}\) por Queremos encontrar\(c \in(-\pi, \pi)\) tal que\(f(c) = 0\).

Ahora, considere la función\[g(x)=\frac{x^{2}}{2}+\sum_{k=1}^{n}\left(-a_{k} \frac{\cos (k x)}{k}+b_{k} \frac{\sin (k x)}{k}\right) .\] Observar eso\(g(-\pi)=g(\pi)\) y\(g^{\prime} = f\). La conclusión se desprende del teorema de Rolle.

Ejercicio\(4.2.5\).

Contestar

Usa la identidad\ [\ frac {1} {g (b) -g (a)}\ izquierda|\ begin {array} {cc}
f (a) & f (b)\
g (a) & g (b)
\ end {array}\ right|=\ frac {f (a) g (b) -f (b) g (a)} {g (b) -g (a))} =\ frac {\ frac {f (a)} {g (a)} -\ frac {f (b)} {g (b)}} {\ frac {1} {g (a)} -\ frac {1} {g (b)}.\] Luego aplica el valor medio de Cauchy teorema para dos funciones\(\phi(x)=\frac{f(x)}{g(x)}\) y\(\psi(x)=\frac{1}{g(x)}\) en el intervalo\([a, b]\).

Ejercicio\(4.2.6\).

Contestar

1. Dado\(\varepsilon > 0\), primero encuentra lo suficientemente\(x_{0}\) grande como\(\psi(x)=\frac{1}{g(x)}\) para que para\(x > x_{0}\). Luego usa la identidad\[\frac{f(x)}{x}=\frac{f(x)-f\left(x_{0}\right)+f\left(x_{0}\right)}{x-x_{0}+x_{0}}=\frac{\frac{f(x)-f\left(x_{0}\right)}{x-x_{0}}+\frac{f\left(x_{0}\right)}{x-x_{0}}}{1+\frac{x_{0}}{x-x_{0}}} ,\] y el teorema del valor medio para mostrar que, para\(x\) grandes,\[a-\varepsilon<\frac{f(x)}{x}<a+\varepsilon .\]
2. Utilice el método de la parte (a).
3. Considerar\(f(x) = \sin (x)\).

Ejercicio\(4.3.2\).

Contestar

1. Podemos demostrar que\(f\) es uniformemente continuo\(\mathbb{R}\) por definición. dado cualquiera\(\varepsilon > 0\), elija\(\delta=\left(\frac{\varepsilon}{\ell+1}\right)^{\frac{1}{\alpha}}\) y obtenga\[|f(u)-f(v)| \leq \ell|u-v|^{\alpha}<\ell \delta^{\alpha}=\ell \frac{\varepsilon}{\ell+1}<\varepsilon\] cuando sea\(|u-v|<\delta\). Tenga en cuenta que usamos\(\ell + 1\) aquí en lugar de\(\ell\) para evitar el caso donde\(\ell = 0\).
2. Demostraremos que\(f\) es una función constante demostrando que es diferenciable sobre\(\mathbb{R}\) y\(f^{\prime}(a)=0\) para todos\(a \in \mathbb{R}\). Arreglar cualquier\(a \in \mathbb{R}\). Entonces, para\(x \neq a\),\[\left|\frac{f(x)-f(a)}{x-a}\right| \leq \frac{\ell|x-a|^{\alpha}}{|x-a|}=\ell|x-a|^{\alpha-1} .\] Ya que\(\alpha > 1\), por el teorema squeeze,\[\lim _{x \rightarrow a} \frac{f(x)-f(a)}{x-a}=0 .\] Esto implica que\(f\) es diferenciable en\(a\) y\(f^{\prime}(a)=0\).
3. Podemos verificar que la función\(f(x) = |x|\) satisface el requisito.

A partir de este problema, vemos que sólo es interesante considerar la clase de funciones que satisfacen (4.8) cuando\(\alpha \leq 1\). Se trata de un ejercicio para demostrar que la función\(f(x)=|x|^{1 / 2}\) satisface esta condición con\(\ell = 1\) y\(\alpha=1 / 2\).

Ejercicio\(4.3.3\).

Contestar

Definir la función\[h(x)=g(x)-f(x) .\] Entonces\(h^{\prime}(x)=g^{\prime}(x)-f^{\prime}(x) \geq 0\) para todos\(x \in\left[x_{0}, \infty\right)\). Así,\(h\) es monótona aumentando en este intervalo. De ello se deduce que\[h(x) \geq h\left(x_{0}\right)=g\left(x_{0}\right)-f\left(x_{0}\right)=0 \text { for all } x \geq x_{0} .\] Por lo tanto,\(g(x) \geq f(x)\) para todos\(x \geq x_{0}\).

Ejercicio\(4.3.5\).

Contestar

Aplicar el teorema del valor medio dos veces.

Ejercicio\(4.3.6\).

Contestar

Utilizar la prueba por contradicción.

Ejercicio\(4.4.5\).

Contestar

Supongamos que\[P(x)=a_{0}+a_{1} x+\cdots+a_{n} x^{n} .\] Entonces aplique la regla de L'Hospital repetidamente.

Ejercicio\(4.4.6\).

Contestar

Primero consideramos el caso donde\(n = 1\) obtener ideas para resolver este problema en el caso general. De los teoremas derivados estándar obtenemos que la función es diferenciable en cualquiera\(x \neq 0\) con\[f^{\prime}(x)=2 x^{-3} e^{-\frac{1}{x^{2}}}=\frac{2}{x^{3}} e^{-\frac{1}{x^{2}}} .\] Considerar el límite\[\lim _{x \rightarrow 0} \frac{f(x)-f(0)}{x-0}=\lim _{x \rightarrow 0} \frac{e^{-\frac{1}{x^{2}}}}{x} .\] Dejar\(t=1 / x\) y aplicar la regla L'Hospital rinde\[\lim _{x \rightarrow 0^{+}} \frac{e^{-\frac{1}{x^{2}}}}{x}=\lim _{t \rightarrow \infty} \frac{t}{e^{t^{2}}}=\lim _{t \rightarrow \infty} \frac{1}{2 t e^{t^{2}}}=0 .\] Similarmente, De\[\lim _{x \rightarrow 0^{-}} \frac{e^{-\frac{1}{x^{2}}}}{x}=0 .\] ello se deduce que\(f\) es diferenciable on\(\mathbb{R}\) con\ [f^ {\ prime} (x) =\ left\ {\ begin {array} {ll}
\ frac {2} {x^ {3}} e^ {-\ frac {1} {x^ {2}}}, &\ text {if} x\ neq 0\ text {;}\\
0, &\ text {if} x=0\ text {.}
\ end {array}\ right.\] De manera similar, podemos mostrar que\(f\) es dos veces diferenciable\(\mathbb{R}\) con\ [f^ {\ prime\ prime} (x) =\ left\ {\ begin {array} {ll}
\ left (\ frac {6} {x^ {4}} +\ frac {2} {x^ {6}}\ right) e^ {-\ frac {1} {x^ {2}}}, &\ texto {si} x\ neq 0\ texto {;}\\
0, &\ texto {si} x=0\ texto {.}
\ end {array}\ right.\] Con base en estos cálculos, predecimos que\(f\) es\(n\) tiempos diferenciables para cada uno\(n \in \mathbb{N}\) con\ [f^ {(n)} (x) =\ left\ {\ begin {array} {ll}
P\ left (\ frac {1} {x}\ right) e^ {-\ frac {1} {x^ {2}}}, &\ text {if} x\ ne. q 0\ texto {;}\\
0, &\ text {if} x=0\ text {,}
\ end {array}\ right.\] donde\(P\) es un polinomio. Ahora procedemos a probar esta conclusión por inducción. La conclusión es cierta para\(n = 1\) como se muestra anteriormente. Dado que la conclusión es cierta para algunos\(n \in \mathbb{N}\),\(x \neq 0\) pues tenemos\[f^{(n+1)}(x)=-x^{-2} P^{\prime}\left(\frac{1}{x}\right)+\frac{2}{x^{3}} P\left(\frac{1}{x}\right) e^{-\frac{1}{x^{2}}}=Q\left(\frac{1}{x}\right) e^{-\frac{1}{x^{2}}} ,\] donde también\(Q\) es un polinomio. Es un ejercicio fácil para escribir la fórmula explícita de\(Q\) basado en\(P\). Además, las sucesivas aplicaciones de la regla de l'Hôpital dan\[\lim _{x \rightarrow 0^{+}} \frac{f^{(n)}(x)-f^{(n)}(0)}{x-0}=\lim _{x \rightarrow 0^{+}} \frac{1}{x} P\left(\frac{1}{x}\right) e^{-\frac{1}{x^{2}}}=\lim _{t \rightarrow \infty} \frac{t P(t)}{e^{t^{2}}}=0 .\] De manera similar, podemos demostrar que\[\lim _{x \rightarrow 0^{-}} \frac{f^{(n)}(x)-f^{(n)}(0)}{x-0}=0 .\] Por lo tanto,\(f^{(n+1)}(0)=0\). Hemos demostrado que para cada\(n \in \mathbb{N}\),\(f\) es\(n\) tiempos diferenciables y, entonces,\(f \in C^{n}(\mathbb{R})\). Aquí no necesitamos probar la continuidad de\(f^{(n)}\) porque la diferenciabilidad de\(f^{(n)}\) implica su continuidad.

De manera similar, también podemos mostrar que la función\ [f (x) =\ left\ {\ begin {array} {ll}
e^ {-\ frac {1} {x}}, &\ text {if} x>0\ text {;}\\
0, &\ text {if} x\ leq 0
\ end {array}\ right.\] es\(n\) tiempos diferenciables para cada\(n \in \mathbb{N}\).

Ejercicio\(4.5.1\).

Contestar

Vamos\(f(x)=e^{x}\). Por el teorema de Taylor\(x > 0\), para cualquiera, existe\(c \in (0, x)\) tal que\ [\ begin {alineado}
f (x) &=e^ {x} =\ sum_ {k=0} ^ {m}\ frac {f^ {(k)} (0)} {k!} x^ {k} +\ frac {f^ {(m+1)} (c)} {(m+1)!} c^ {m+1}\\
&=\ sum_ {k=0} ^ {m}\ frac {x^ {k}} {k!} +\ frac {e^ {c}} {(m+1)!} c^ {m+1} >\ sum_ {k=0} ^ {m}\ frac {x^ {k}} {k!}
\ end {alineado}.\]

Ejercicio\(4.5.5\).

Contestar

1. Observe que una versión más simple de este problema se puede afirmar de la siguiente manera: Si\(f\) es diferenciable en\((a, b)\) y\(\bar{x} \in (a, b)\), entonces\[\lim _{h \rightarrow 0} \frac{f(\bar{x}+h)-f(\bar{x})}{h}=\frac{f^{\prime}(\bar{x})}{1 !} .\] Esta conclusión se desprende directamente de la definición de derivado.

De igual manera, si\(f\) es dos veces diferenteaible en\((a, b)\) y\(\bar{x} \in (a, b)\), entonces\[\lim _{h \rightarrow 0} \frac{f(\bar{x}+h)-f(\bar{x})-f^{\prime}(\bar{x}) \frac{h}{1 !}}{h^{2}}=\frac{f^{\prime \prime}(\bar{x})}{2 !} .\] podemos probarlo aplicando la regla de L'Hospital para obtener Ahora está\[\lim _{h \rightarrow 0} \frac{f(\bar{x}+h)-f(\bar{x})-f^{\prime}(\bar{x}) \frac{h}{1 !}}{h^{2}}=\lim _{h \rightarrow 0} \frac{f^{\prime}(\bar{x}+h)-f^{\prime}(\bar{x})}{2 h}=\frac{f^{\prime \prime}(\bar{x})}{2 !} .\] claro que podemos resolver la parte (a) utilizando la regla de L'Hospital de la siguiente manera:\[\lim _{h \rightarrow 0} \frac{f(\bar{x}+h)-f(\bar{x})-f^{\prime}(\bar{x}) \frac{h}{1 !}-f^{\prime \prime}(\bar{x}) \frac{h^{2}}{2 !}}{h^{3}}=\lim _{h \rightarrow 0} \frac{f^{\prime}(\bar{x}+h)-f^{\prime}(\bar{x})-f^{\prime \prime}(\bar{x}) \frac{h}{1 !}}{3 h^{2}}=\frac{f^{\prime \prime \prime}(\bar{x})}{3 !} .\] Obsérvese que la última igualdad se desprende de la prueba previa aplicada a la función\(f^{\prime}\).

2. Con el análisis de la parte (a), vemos que si\(f\) es\(n\) tiempos diferenciables en\((a, b)\) y\(\bar{x} \in (a, b)\), entonces\[\lim _{h \rightarrow 0} \frac{f(\bar{x}+h)-\sum_{k=0}^{n-1} \frac{f^{(k)}(\bar{x}) h^{k}}{k !}}{h^{n+1}}=\frac{f^{(n)}(\bar{x})}{n !} .\] Esta conclusión se puede probar por inducción. Este resultado general se puede aplicar para obtener la expansión Taylor con el resto de Peano en Ejercitador 4.5.6.

Ejercicio\(4.6.3\).

Contestar

Aplicamos la definición para resolver este problema. Dado cualquiera\(u, v \in I\) y\(\lambda \in (0, 1)\), tenemos\[f(\lambda u+(1-\lambda) v) \leq \lambda f(u)+(1-\lambda) f(v)\] por la convexidad de\(f\).

Desde\(f(u), f(v) \in J\) y\(J\) es un intervalo,\(\lambda f(u)+(1-\lambda) f(v) \in J\). Por la propiedad no decreciente y la convexidad de\(\phi\). \[\phi(f(\lambda u+(1-\lambda) v)) \leq \phi(\lambda f(u)+(1-\lambda) f(v)) \leq \lambda \phi(f(u))+(1-\lambda) \phi(f(v)).\]Por lo tanto,\(\phi \circ f\) es convexo en\(I\).

El resultado de este problema nos permite generar funciones convexas. Por ejemplo, considere\(f(x) = |x|\) y\(\phi(x)=x^{p}\),\(p > 1\). Hemos visto que\(f\) es convexo en\(\mathbb{R}\). La función\(\phi\) es convexa y creciente en la\([0, \infty)\) que contiene el rango de la función\(f\). Por lo tanto, la composición\(g(x)=|x|^{p}\),\(p > 1\), es convexa en\(\mathbb{R}\). Del mismo modo, también\(h(x)=e^{x^{2}}\) es una función convexa en\(\mathbb{R}\).

Observe que en este problema, requerimos la propiedad no decreciente de\(\phi\). Una cuestión natural es si la composición de dos funciones convexas es convexa. La respuesta es negativa. Observe eso\(f(x) = x^{2}\) y\(h(x)=e^{x^{2}}\phi(x)=|x-1|\) son convexos, pero\((\phi \circ f)(x)=\left|x^{2}-1\right|\) no convexos.

Ejercicio\(4.6.4\).

Contestar

1. Utilizar la desigualdad obvia\[(\sqrt{a}-\sqrt{b})^{2} \geq 0 .\] Alternativamente, considere la función\(f(x)=-\ln (x)\),\(x \in (0, \infty)\). Podemos mostrar que\(f\) es convexo en\((0, \infty)\). Porque\(a, b \in (0, \infty)\), uno tiene\[f\left(\frac{a+b}{2}\right) \leq \frac{f(a)+f(b)}{2} .\] Esto implica\[-\ln \left(\frac{a+b}{2}\right) \leq \frac{-\ln (a)-\ln (b)}{2}=-\ln (\sqrt{a b}) .\] Por lo tanto,\[\frac{a+b}{2} \geq \sqrt{a b} .\] Esta desigualdad sostiene obviamente cuándo\(a = 0\) o\(b = 0\).
2. Utilice el Teorema 4.6.3 para la función\(f(x)=-\ln (x)\) on\((0, \infty)\).

Ejercicio\(4.7.1\).

Contestar

1. Por Teorema 4.7.5,\ [\ parcial f (x) =\ left\ {\ begin {array} {ll}
   \ {-a\}, &\ text {if} x<0\ text {;}\\
   {[-a, a],} &\ text {if} x=0\ text {;}\\
   \ {a\}, &\ text {si} x>0\ text {.}
   \ end {array}\ derecho.\]
2. Por Teorema 4.7.5,\ [\ parcial f (x) =\ left\ {\ begin {array} {ll}
   \ {-2\}, &\ text {if} x<-1\ text {;}\\
   {[-2,0],} &\ text {if} x=-1\ text {;}\\
   \ {0\}, &\ text {si} x\ in (-1,1)\ texto {;}\\
   {[0,2],} &\ texto {si} x=1\ text {;}\\
   \ {2\}, &\ text {if} x>1\ text {.}
   \ end {array}\ derecho.\]

Ejercicio\(4.7.3\).

Contestar

Para entender mejor el problema, consideramos algunos casos especiales. Si\(n = 1\), entonces\(f(x)=|x-1|\). Obviamente,\(f\) tiene un mínimo absoluto en\(x = 1\). Si\(n = 2\), entonces\(f(x)=|x-1|+|x-2|\). La gráfica de la función sugiere que\(f\) tiene un mínimo absoluto en cualquiera\(x \i [1, 2]\). En el caso donde\(n = 3\), podemos ver que\(f\) tiene un mínimo absoluto en\(x = 2\). Entonces conjeturamos que si\(n\) es impar con\(n=2 m-1\), entonces\(f\) tiene un mínimo absoluto en\(x = m\). Si\(n\) es par con\(n = 2m\), entonces\(f\) tiene un mínimo absoluto en cualquier momento\(x \in[m, m+1]\).

Demostremos la primera conclusión. En este caso,\[f(x)=\sum_{i=1}^{2 m-1}|x-i|=\sum_{i=1}^{2 m-1} f_{i}(x) ,\] donde\(f_{i}(x)=|x-i|\). Considerar\(\bar{x} = m\). Entonces\[\partial f_{m}(\bar{x})=[-1,1], \partial f_{i}(\bar{x})=\{1\} \text { if } i<m, \partial f_{i}(\bar{x})=\{-1\} \text { if } i>m .\] La regla de suma subdiferencial rinde\(\partial f(\bar{x})=[-1,1]\) que contiene\(0\). Así,\(f\) tiene un mínimo absoluto en\(\bar{x}\). Si\(\bar{x} > m\), podemos ver eso\(\partial f(\bar{x}) \subset(0, \infty)\), que no contiene\(0\). Del mismo modo, si\(\bar{x} < m\), entonces\(\partial f(\bar{x}) \subset(-\infty, 0)\). Por lo tanto,\(f\) tiene un mínimo absoluto en el único punto\(\bar{x} = m\).

El caso donde\(n\) está incluso se puede tratar de manera similar.

Ejercicio\(4.7.5\).

Contestar

Arreglar\(a, b \in \mathbb{R}\) con\(a < b\). Por Teorema 4.7.9, existe\(c \in (a, b)\) tal que\[\frac{f(b)-f(a)}{b-a} \in \partial f(c) \subset[0, \infty) .\] Esto implica\(f(b)-f(a) \geq 0\) y, por lo tanto,\(f(b) \geq f(a)\). Por lo tanto,\(f\) es monótona aumentando en\(\mathbb{R}\).