2.1: Newton y Leibniz Comenzar

Objetivos de aprendizaje

• Explicar el enfoque de Leibniz a la Regla del Producto
• Explicar el enfoque de Newton a la regla del producto

Reglas de Cálculo de Leibniz

Las reglas para el cálculo se establecieron por primera vez en el artículo de 1684 de Gottfried Wilhelm Leibniz Nova methodus pro maximis et minimis, itemque tangentibus, quae nec fractas nec irrationales, quantitates moratur, et singulare pro illi calculi genus (A New Method for Maxima and Minima as Well as Tangents, Which no se ve obstaculizado ni por cantidades fraccionarias ni irracionales, y un tipo notable de cálculo para esto).

Figura\(\PageIndex{1}\): Gottfried Wilhelm Leibniz.

Leibniz comenzó con la resta. Es decir, si\(x_1\) y\(x_2\) están muy unidos entonces su diferencia,\(∆x = x_2 - x_1\), es muy pequeña. Amplió esta idea para decir que si\(x_1\) y\(x_2\) están infinitamente juntos (pero aún así distintos) entonces su diferencia,\(dx\), es infinitesimalmente pequeña (pero no cero).

Esta idea es lógicamente muy sospechosa y Leibniz la sabía. Pero también sabía que cuando usaba su cálculo diferencial ¹ estaba obteniendo respuestas correctas a algunos problemas muy duros. Por lo que perseveró.

Leibniz llamó a ambos\(∆x\) y\(dx\) “diferenciales” (latín para diferencia) porque pensaba en ellos como, esencialmente, lo mismo. Con el tiempo se ha hecho costumbre referirse a lo infinitesimal\(dx\) como diferencial, reservándose “diferencia” para el caso finito,\(∆x\). Esta es la razón por la cual el cálculo a menudo se llama “cálculo diferencial”.

En su ponencia Leibniz dio reglas para hacer frente a estos diferenciales infinitamente pequeños. Específicamente, dada una cantidad variable\(x\),\(dx\) representó un cambio infinitesimal en\(x\). Los diferenciales se relacionan a través de la pendiente de la línea tangente a una curva. Es decir, si\(y = f(x)\), entonces\(dy\) y\(dx\) están relacionados por

\[dy = \text{(slope of the tangent line)}\cdot dx\]

Leibniz luego dividió\(dx\) dando

\[\frac{dy}{dx} = \text{(slope of the tangent line)}\]

La notación elegante y expresiva que inventó Leibniz fue tan útil que se ha conservado a través de los años a pesar de algunos cambios profundos en los conceptos subyacentes. Por ejemplo, Leibniz y sus contemporáneos habrían visto el símbolo\(\frac{dy}{dx}\) como un cociente real de infinitesimales, mientras que hoy lo definimos a través del concepto límite sugerido por primera vez por Newton.

Como resultado, las reglas que rigen estos diferenciales son de apariencia muy moderna:

\[d(constant) = 0\]

\[d(z - y + w + x) = dz - dy + dw + dx\]

\[d(xv) = xdv + v dx\]

\[d\left ( \frac{v}{y} \right ) = \frac{ydv - vdy}{yy}\]

y, cuando\(a\) es un entero:

\[d(x^a) = ax^{a - 1} dx\]

Leibniz afirma estas reglas sin pruebas: “.. la demostración de todo esto será fácil para quien tenga experiencia en tales asuntos... ” Como ejemplo, se esperaría que los matemáticos en la época de Leibniz entendieran intuitivamente que si\(c\) es una constante, entonces\(d(c) = c - c = 0\). De igual manera,\(d(x + y) = dx + dy\) es realmente una extensión de\((x_2 + y_2) - (x_1 + y_1) = (x_2 - x_1) + (y_2 - y_1)\).

Aproximación de Leibniz a la regla del producto

La explicación de la regla del producto usando diferenciales es un poco más involucrada, pero Leibniz esperaba que los matemáticos fueran lo suficientemente fluentes como para derivarlo. El producto se\(p = xv\) puede considerar como el área del siguiente rectángulo

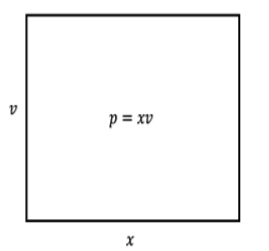
Figura\(\PageIndex{2}\): Área de un rectángulo.

Con esto en mente,\(dp = d(xv)\) puede pensarse como el cambio de área cuando\(x\) es cambiado por\(dx\) y\(v\) es cambiado por\(dv\). Esto se puede ver como la región\(L\) conformada en el siguiente dibujo.

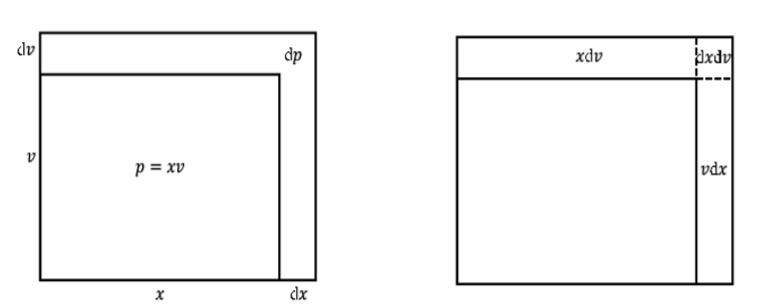
Figura\(\PageIndex{3}\): Cambio de área cuando\(x\) es cambiado por\(dx\) y\(v\) es cambiado por\(dv\).

Al dividir la región\(L\) conformada en\(3\) rectángulos obtenemos

\[d(xv) = xdv + v dx + dx dv\]

A pesar de que\(dx\) y\(dv\) son infinitamente pequeños, Leibniz razonó que\(dx dv\) es aún más infinitamente pequeño (¿cuadráticamente infinitamente pequeño?) comparado con\(xdv\) y\(vdx\) y por lo tanto puede ser ignorado dejando

\[d(xv) = xdv + v dx\]

Deberías sentir cierta incomodidad ante la idea de simplemente echar el producto\(dx dv\) a un lado porque es “comparativamente pequeño. ” Esto significa que has estado bien entrenado, y has interiorizado a fondo el dictum de Newton [10]: “Los errores más pequeños no pueden, en materia matemática, ser despreciados. ” Lógicamente es insostenible echar a un lado una expresión solo porque es pequeña. Y menos aún deberíamos estar dispuestos a ignorar una expresión con el argumento de que es “infinitamente más pequeña” que otra cantidad que en sí misma es “infinitamente pequeña”. ”

Newton y Leibniz ambos sabían esto tan bien como nosotros. Pero también sabían que sus métodos funcionaban. Ellos dieron respuestas verificablemente correctas a problemas que, hasta ahora, habían sido completamente intratables. Es la marca de su genio que ambos hombres perseveraron a pesar de las dificultades muy evidentes que implicaban sus métodos.

El enfoque de Newton a la regla del producto

En los Principia, Newton “probó” la Regla del Producto de la siguiente manera: Dejar\(x\) y\(v\) ser “^{flotando 2} cuantitos” y considerar el rectángulo\(R\),, cuyos lados son\(x\) y\(v\). \(R\)es también una cantidad floreciente y deseamos encontrar su fluxion (derivado) en cualquier momento.

Figura\(\PageIndex{4}\): Isaac Newton

Primer incremento\(x\) y\(v\) por\(\frac{∆x}{2} \) y\(\frac{∆v}{2} \) respectivamente. Entonces el incremento correspondiente de\(R\) es

\[\left ( x + \frac{\Delta x}{2} \right ) \left ( v + \frac{\Delta v}{2} \right ) = xv + x\frac{\Delta v}{2} + v\frac{\Delta x}{2} + \frac{\Delta x \Delta v}{4}\]

Ahora decremento\(x\) y\(v\) por las mismas cantidades:

\[\left ( x - \frac{\Delta x}{2} \right ) \left ( v - \frac{\Delta v}{2} \right ) = xv - x\frac{\Delta v}{2} - v\frac{\Delta x}{2} + \frac{\Delta x \Delta v}{4}\]

Restar el lado derecho de la ecuación\(\PageIndex{11}\) del lado derecho de la ecuación\(\PageIndex{10}\) da

\[∆R = x∆v + v∆x\]

que es el cambio total de\(R = xv\) a lo largo de los intervalos\(∆x\)\(∆v\) y también reconociblemente la Regla del Producto.

Este argumento no es mejor que el de Leibniz ya que se basa en gran medida en el número\(1/2\) para que funcione. Si tomamos cualquier otro incremento en\(x\) y\(v\) cuyas longitudes totales son\(∆x\) y simplemente no\(∆v\) va a funcionar. Pruébalo y mira.

En defensa de Newton, en realidad no estaba tratando de justificar sus métodos matemáticos en los Principia. Su atención ahí estaba en la física, no en las matemáticas, así que en realidad solo estaba tratando de dar una demostración convincente de sus métodos. Puedes decidir por ti mismo lo convincente que es su manifestación.

Observe que no se mencionan límites de cocientes de diferencia o derivados. De hecho, el término derivado no fue acuñado hasta 1797, por Lagrange. En cierto sentido, estos temas no eran necesarios en su momento, ya que Leibniz y Newton asumieron que las curvas que trataban tenían líneas tangentes y, de hecho, Leibniz utilizó explícitamente la línea tangente para relacionar dos cantidades diferenciales. Esto fue congruente con el pensamiento de la época y durante la duración de este capítulo también asumiremos que todas las cantidades son diferenciables. Como veremos más adelante esta suposición lleva a dificultades.

Tanto Newton como Leibniz se mostraron satisfechos de que su cálculo proporcionara respuestas que coincidieron con lo que se sabía en su momento. Por ejemplo\(d(x^2)= d(xx) = xdx+xdx = 2xdx\) y\(d(x^3)= d(x^2x)= x^2 dx+xd(x^2)= x^2+x(2xdx) = 3x^2 dx\), resultados que esencialmente fueron derivados por otros de diferentes maneras.

Ejercicio\(\PageIndex{1}\)

1. Usa la regla de producto de Leibniz\(d(xv) = xdv + vdx\) para mostrar que si\(n\) es un entero positivo entonces\(d(x^n) = nx^{n - 1} dx\)
2. Usar la regla de producto de Leibniz para derivar la regla del cociente\[d \left ( \frac{v}{y} \right ) = \frac{ydv - vdy}{yy}\]
3. Usa la regla del cociente para mostrar que si es un entero positivo, entonces\[d(x^{-n}) = -nx^{-n - 1} dx\]

Ejercicio\(\PageIndex{2}\)

Dejar\(p\) y\(q\) ser enteros con\(q\neq 0\). Mostrar\[d\left ( x^{\frac{p}{q}} \right ) = \frac{p}{q} x^{\frac{p}{q} - 1} dx\]

Leibniz también aportó aplicaciones de su cálculo para demostrar su valía. Como ejemplo derivó la Ley de Refracción de Snell a partir de sus reglas de cálculo de la siguiente manera.

Dado que la luz viaja a través del aire a una velocidad de\(v_a\) y viaja a través del agua a una velocidad\(v_w\) del problema es encontrar el camino más rápido de punto\(A\) a punto\(B\).

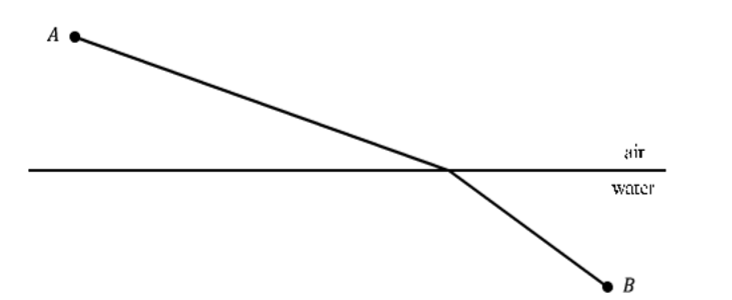
Figura\(\PageIndex{5}\): Trayectoria más rápida que la luz recorre de punto\(A\) a punto\(B\).

Según el Principio del Menor Tiempo de Fermat, este camino más rápido es el que recorrerá la luz.

Utilizando el hecho de que\(Time = Distance/Velocity\) y el etiquetado en la imagen de abajo podemos obtener una fórmula para el tiempo\(T\) que tarda la luz en viajar de\(A\) a\(B\).

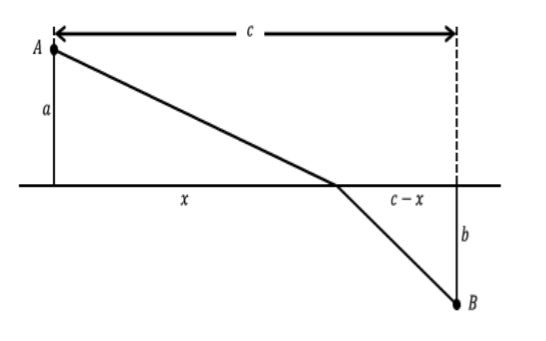
Figura\(\PageIndex{6}\): Principio del Menor Tiempo de Fermat.

\[T = \frac{\sqrt{x^2 + a^2}}{v_a} + \frac{\sqrt{(c-x)^2 + b^2}}{v_w}\]

Usando las reglas del cálculo de Leibniz, obtenemos

\[\begin{align*} dT &= \left ( \frac{1}{v_a} \frac{1}{2} (x^2 + a^2)^{-\frac{1}{2}} (2x) + \frac{1}{v_w} \frac{1}{2} ((c-x)^2 + b^2)^{-\frac{1}{2}} (2(c-x)(-1))\right )dx\\ &= \left ( \frac{1}{v_a} \frac{x}{\sqrt{x^2 + a^2}} - \frac{1}{v_w} \frac{c-x}{\sqrt{(c-x)^2 + b^2}} \right )dx \end{align*}\]

Utilizando el hecho de que al valor mínimo para\(T\),\(dT = 0\), tenemos que el camino más rápido de\(A\) a\(B\) debe satisfacer\(\frac{1}{v_a} \frac{x}{\sqrt{x^2 + a^2}} = \frac{1}{v_w} \frac{c-x}{\sqrt{(c-x)^2 + b^2}}\). Inserción de los siguientes ángulos

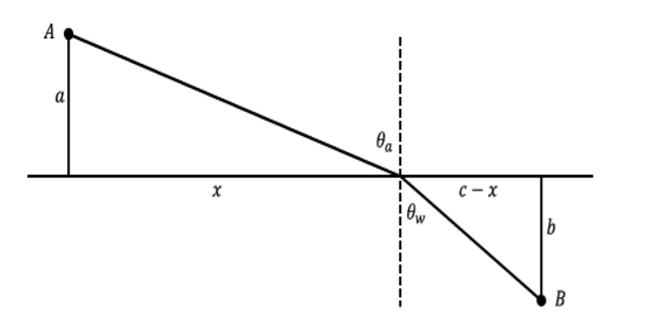
Figura\(\PageIndex{7}\): El camino más rápido que recorre la luz.

conseguimos que el camino que recorre la luz debe satisfacer

\[\frac{\sin \theta _a}{v_a} = \frac{\sin \theta _w}{v_w}\]

que es la Ley de Snell.

Para comparar las técnicas\(18^{th}\) del siglo y las modernas consideraremos la solución de Johann Bernoulli al problema de Brachistochrone. En 1696, Bernoulli planteó, y resolvió, el problema de Brachistochrone; es decir, encontrar la forma de un alambre sin fricción que une puntos\(A\) y para\(B\) que el tiempo que tarda una perla en deslizarse hacia abajo bajo la fuerza de la gravedad sea lo más pequeño posible.

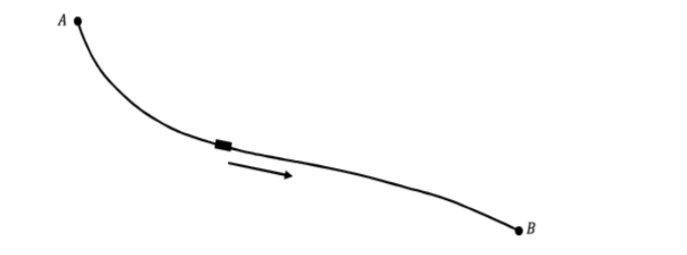
Figura\(\PageIndex{8}\): Encontrar la forma de un alambre sin fricción puntos de unión\(A\) y\(B\).

Bernoulli planteó este problema de “camino de descenso más rápido” para desafiar a los matemáticos de Europa y utilizó su solución para demostrar el poder del cálculo de Leibniz así como su propio ingenio.

Yo, Johann Bernoulli, me dirijo a los matemáticos más brillantes del mundo. Nada es más atractivo para las personas inteligentes que un problema honesto y desafiante, cuya posible solución otorgará fama y permanecerá como un monumento duradero. Siguiendo el ejemplo de Pascal, Fermat, etc., espero ganar la gratitud de toda la comunidad científica poniendo ante los mejores matemáticos de nuestro tiempo un problema que pondrá a prueba sus métodos y la fuerza de su intelecto. Si alguien me comunica la solución del problema propuesto, lo declararé públicamente digno de elogio [11].

Figura\(\PageIndex{9}\): Johann Bernoulli.

Además de las de Johann, se obtuvieron soluciones de Newton, Leibniz, el hermano de Johann, Jacob Bernoulli, y el marqués de l'Hopital [15]. En su momento hubo una polémica permanente y muy vitriólica que se desataba sobre si Newton o Leibniz habían sido los primeros en inventar el cálculo. Defensor de los métodos de Leibniz, Bernoulli no creía que Newton pudiera resolver el problema usando sus métodos. Bernoulli intentó avergonzar a Newton enviándole el problema. Sin embargo Newton sí lo resolvió.

En este punto de su vida Newton casi había renunciado a la ciencia y las matemáticas y estaba totalmente enfocado en sus funciones administrativas como Maestro de la Casa de la Moneda. En parte debido a la falsificación desenfrenada, el dinero de Inglaterra se había devaluado severamente y la nación estaba al borde del colapso económico. La solución fue recordar todas las monedas existentes, derretirlas y golpear otras nuevas. Como Maestro de la Casa de la Moneda este trabajo recayó en Newton [8]. Como podríais imaginar esta era una tarea bastante hercúleana. Sin embargo, según su sobrina:

Cuando el problema en 1696 fue enviado por Bernoulli—Sir I.N. estaba en medio de la prisa del gran recoinage y no llegó a casa hasta las cuatro de la Torre muy cansado, pero no durmió hasta que lo había resuelto, que era a las cuatro de la mañana. (citado en [2], página 201)

Más tarde se informa que se ha quejado, “no me encanta... ser... tediado por forreinadores sobre las cosas matemáticas [2]”.

Newton presentó su solución de forma anónima, presumiblemente para evitar más polémica. Sin embargo, los métodos utilizados fueron tan distintivamente los de Newton que se dice que Bernoulli exclamó “Tanquam ex ungue leonem. ” ³

La ingeniosa solución de Bernoulli comienza, curiosamente, con la Ley de Refracción de Snell. Comienza considerando el medio estratificado en la siguiente figura, donde un objeto viaja con velocidades\(v_1, v_2, v_3, ...\) en las distintas capas.

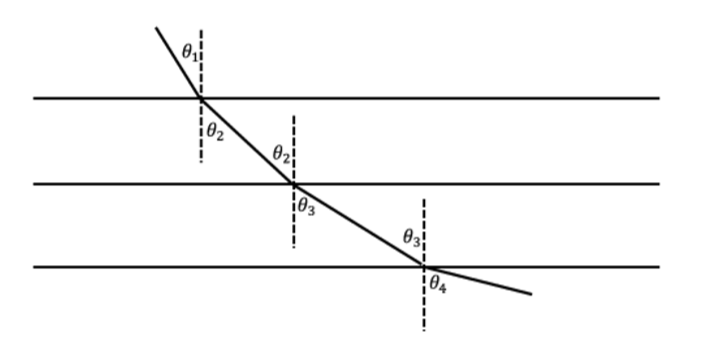
Figura\(\PageIndex{10}\): Solución de Bernoulli.

Al aplicar repetidamente la Ley de Snell concluyó que el camino más rápido debe satisfacer

\[\frac{\sin \theta _1}{v_1} = \frac{\sin \theta _2}{v_2} = \frac{\sin \theta _3}{v_3} = \cdots\]

Es decir, la relación del seno del ángulo que hace la curva con la vertical y la velocidad permanece constante a lo largo de este camino más rápido.

Si pensamos en un medio en continuo cambio estratificado en capas infinitesimales y extendemos la ley de Snell a un objeto cuya velocidad cambia constantemente,

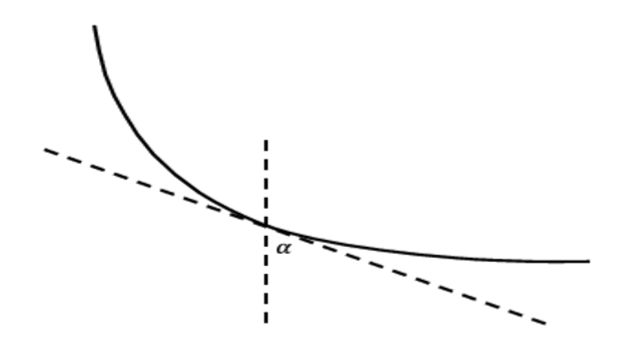
Figura\(\PageIndex{11}\): Ley de Snell para un objeto que cambia la velocidad continuamente.

entonces a lo largo del camino más rápido, la relación del seno del ángulo que la tangente de la curva hace con la vertical\(α\), y la velocidad,\(v\), debe permanecer constante.

\[\frac{\sin \alpha }{v} = c\]

Si incluimos ejes y dejamos\(P\) denotar la posición de la cuenta en un momento determinado entonces tenemos la siguiente imagen.

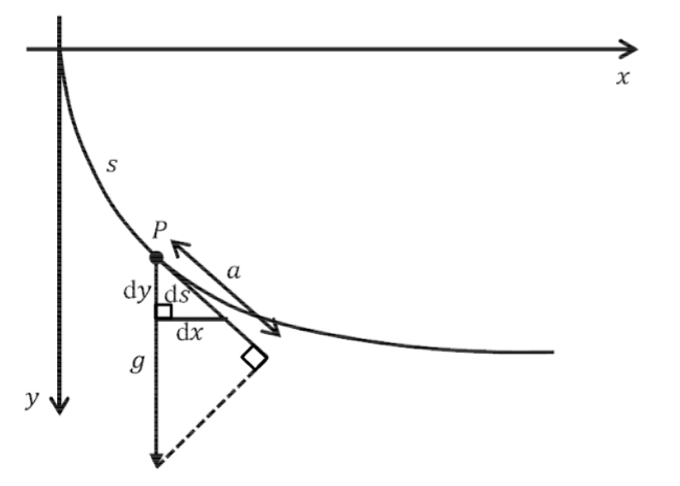
Figura\(\PageIndex{11}\): Trayectoria recorrida por la cuenta.

En la figura anterior,\(s\) denota la longitud que la perla ha recorrido hacia abajo hasta el punto\(P\) (es decir, la longitud del arco de la curva desde el origen hasta ese punto) y a denota la componente tangencial de la aceleración por gravedad\(g\). Dado que la cuenta viaja solo bajo la influencia de la gravedad entonces\(\frac{dv}{dt} = a\).

Para tener una idea de cómo se abordaron los problemas físicos usando el cálculo de Leibniz usaremos la ecuación anterior para demostrarlo\(v = \sqrt{2gy}\).

Por triángulos similares tenemos\(\frac{a}{g} = \frac{dy}{ds}\). Como estudiante de Leibniz, Bernoulli habría considerado\(\frac{dy}{ds}\) como una fracción así

\[a ds = gdy\]

y como la aceleración es la tasa de cambio de velocidad tenemos

\[\frac{dv}{dt} ds= gdy\]

Una vez más, los matemáticos europeos\(18^{th}\) del siglo consideraron\(dv\)\(dt\), y\(ds\) como números infinitesimalmente pequeños que, sin embargo, obedecen todas las reglas habituales del álgebra. Así podemos reorganizar lo anterior para obtener

\[\frac{ds}{dt} dv= gdy\]

Ya que\(\frac{ds}{dt}\) es la tasa de cambio de posición con respecto al tiempo es, de hecho, la velocidad de la perla. Eso es

\[v dv = g dy\]

Bernoulli habría interpretado esto como una afirmación de que dos rectángulos de altura\(v\) y\(g\), con anchuras respectivas\(dv\) y\(dy\) tienen igual área. Sumando (integrando) todos esos rectángulos obtenemos:

\[\int v dv = \int g dy\]

\[\frac{v^2}{2} = gy\]

o

\[v = \sqrt{2gy}\]

Sin duda te sientes incómodo con la manipulación arrogante de cantidades infinitesimales que acabas de presenciar, así que haremos una pausa por un momento para comparar un desarrollo moderno de la ecuación\(\PageIndex{12}\) con el de Bernoulli.Como antes comenzamos con la ecuación:

\[\frac{a}{g} = \frac{dy}{ds}\]

\[a = g\frac{dy}{ds}\]

Además, dado que la aceleración es la derivada de la velocidad, esto es lo mismo que:

\[\frac{dv}{dt} = g\frac{dy}{ds}\]

Ahora observa eso por la Regla de las Cadenas\(\frac{dv}{dt} = \frac{dv}{ds} \frac{ds}{dt}\). La interpretación física de esta fórmula es que la velocidad dependerá de\(s\), qué tan abajo del alambre se haya movido la cuenta, pero que la distancia recorrida dependerá de cuánto tiempo haya transcurrido. Por lo tanto

\[\frac{dv}{ds} \frac{ds}{dt} = g\frac{dy}{ds}\]

o

\[\frac{ds}{dt} \frac{dv}{ds} = g\frac{dy}{ds}\]

y desde\(\frac{ds}{dt} = v\)

\[v\frac{dv}{ds} = g\frac{dy}{ds}\]

Integrando ambas partes con respecto a\(s\) da:

\[\int v\frac{dv}{ds} ds = g\int \frac{dy}{ds} ds\]

\[\int vdv = g\int dy\]

e integrando da

\[\frac{v^2}{2} = gy\]

como antes.

En efecto, en la formulación moderna hemos cambiado la simplicidad y elegancia de los diferenciales por un uso repetido comparativamente engorroso de la Regla de Cadena. Sin duda se dio cuenta al tomar Cálculo que en la notación diferencial de Leibniz, la Regla de Cadena parece “cancelar” una expresión en la parte superior e inferior de una fracción:\(\frac{dy}{du} \frac{du}{dx} = \frac{dy}{dx}\). Esto se debe a que para los matemáticos del siglo XVIII, esto es exactamente lo que era.

Para decirlo de otra manera, los matemáticos\(18^{th}\) del siglo no habrían reconocido la necesidad de lo que llamamos la Regla de las Cadenas porque esta operación era una trivialidad para ellos. Solo reduce la fracción. Esto plantea la pregunta: ¿Por qué abandonamos una interpretación tan clara y simple de nuestros símbolos en favor de la interpretación moderna, comparativamente, más engorrosa? Esta es una de las preguntas que trataremos de responder en este curso.

Volviendo al problema de Brachistochrone observamos eso\(\frac{\sin \alpha }{v} = c\) y como\(\sin \alpha = \frac{dx}{ds}\) vemos que

\[\frac{\frac{dx}{ds}}{\sqrt{2gy}} = c\]

\[\frac{dx}{\sqrt{2gy(ds)^2}} = c\]

\[\frac{dx}{\sqrt{2gy\left [ (dx)^2 + (dy)^2 \right ]}} = c\]

Bernoulli fue entonces capaz de resolver esta ecuación diferencial.

Ejercicio\(\PageIndex{3}\)

Demostrar que las ecuaciones\(x = \frac{t - \sin t}{4gc^2}\),\(y = \frac{t - \cos t}{4gc^2}\) satisfacen ecuación\(\PageIndex{37}\). Bernoulli reconoció que esta solución era un cicloide invertido, la curva trazada por un punto fijo en un círculo a medida que el círculo rueda a lo largo de una superficie horizontal.

Esto ilustra el estado del cálculo a finales de los 1600 y principios del 1700; los fundamentos del tema eran un poco temblorosos pero no se podía negar su poder.

Referencias

¹ Esto se traduce, vagamente, como el cálculo de las diferencias.

² El enfoque de Newton al cálculo —su 'Método de Fluxiones'— dependía fundamentalmente del movimiento. Es decir, veía sus variables (fluentes) como cambiantes (floreciendo o flotando) en el tiempo. La tasa de cambio de un fluent que llamó fluxion. Como fundamento tanto los planteamientos de Leibniz como los de Newton han caído en desgracia, aunque ambos siguen siendo utilizados universalmente como un enfoque conceptual, una “forma de pensar”, sobre las ideas del cálculo.

³ Conozco al león por su garra.