3.2: Anomalías en serie
- Page ID
- 109496
- Explicar la convergencia de series y las anomalías
Hasta este punto, hemos sido algo frívolos en nuestro acercamiento a las series. Este enfoque refleja a matemáticos del siglo XVIII que explotaron ingeniosamente el cálculo y las series para proporcionar resultados matemáticos y físicos que antes eran prácticamente inalcanzables. Los matemáticos estaban ansiosos por impulsar estas técnicas en la medida de lo posible para obtener sus resultados y muchas veces mostraban buena intuición respecto a lo que era matemáticamente aceptable y lo que no lo era. Sin embargo, a medida que se empujaba el sobre, surgieron preguntas sobre la validez de los métodos.
Como ilustración considere la expansión de la serie
\[\frac{1}{1+x} = 1 - x + x^2 - x^3 + \cdots\]
Si sustituimos\(x = 1\) en esta ecuación, obtenemos
\[\frac{1}{2} = 1 - 1 + 1 - 1 + \cdots\]
Si agrupamos los términos de la siguiente manera\((1-1)+(1-1)+···\), la serie sería igual\(0\). Un reagrupamiento de\(1 + (-1 + 1) + (-1 + 1) +···\) proporciona una respuesta de\(1\). Esta violación a la ley asociativa de adición no escapó a los matemáticos de la década de 1700. En su artículo de 1760 On Divergent Series Euler dijo:
Suficientemente notables, sin embargo son las controversias sobre la serie\(1 - 1 + 1 - 1 +\) etc, cuya suma fue dada por Leibniz como\(\frac{1}{2}\), aunque otras no están de acuerdo. La comprensión de esta cuestión debe buscarse en la palabra “suma”; esta idea, si así se concibe a saber, se dice que la suma de una serie es aquella cantidad a la que se acerca a medida que se toman más términos de una serie -tiene relevancia sólo para la serie convergente, y en general debemos renunciar a esta idea de suma para series divergentes. Por otra parte, como las series en análisis surgen de la expansión de fracciones o cantidades irracionales o incluso de trascendentales, será permisible, a su vez, en el cálculo sustituir en lugar de tales series aquella cantidad de cuyo desarrollo se produce.
Incluso con este enfoque formal de las series, surge una pregunta interesante. La serie para la antiderivada de\(\frac{1}{1+x}\) sí converge\(x = 1\) mientras ésta no. Específicamente, tomando el antiderivado de la serie anterior, obtenemos
\[\ln (1+x) = x - \frac{1}{2}x^2 + \frac{1}{3}x^3 - \cdots\]
Si sustituimos\(x = 1\) en esta serie, obtenemos\(\ln 2 = 1 - \frac{1}{2} + \frac{1}{3} - \cdots\). No es difícil ver que converge una serie alternante de este tipo. El siguiente cuadro muestra por qué. En este diagrama,\(S_n\) denota la suma parcial\(\ln 2 = x - \frac{1}{2} + \frac{1}{3} - \cdots + \frac{(-1)^{n+1}}{n}\).
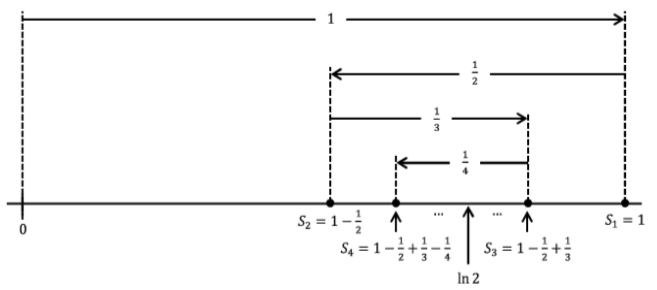
Figura\(\PageIndex{1}\): Convergencia en serie.
Del diagrama podemos ver\(S_2 ≤ S_4 ≤ S_6 ≤···≤···≤ S_5 ≤ S_3 ≤ S_1\) y\(S_{2k+1} - S_{2k} = \frac{1}{2k+1}\). Parece que la secuencia de sumas parciales convergerá a lo que esté en el “medio”. Nuestro diagrama indica que está\(\ln 2\) en el medio pero en realidad esto no es obvio. No obstante es interesante que una serie converja para\(x = 1\) pero la otra no.
Usa el hecho de que
\[1 - \frac{1}{2} + \frac{1}{3} - \cdots + \frac{(-1)^{2k+1}}{2k} \leq \ln 2 \leq 1 - \frac{1}{2} + \frac{1}{3} - \cdots + \frac{(-1)^{2k+2}}{2k+1}\]
para determinar cuántos términos de la serie\(\sum_{n=0}^{\infty } \frac{(-1)^{n+1}}{n}\) deben sumarse para aproximarse\(\ln 2\) a dentro\(0.0001\) sin realmente computar lo que\\(ln 2\) es.
Hay una situación aún más desconcertante que traen consigo estos ejemplos. Una suma infinita como\(1 - 1 + 1 - 1 + ···\) parece no satisfacer la ley asociativa para la adición. Si bien una serie convergente como la que\(1 - \frac{1}{2} + \frac{1}{3} - \cdots\) satisface la ley asociativa, no satisface la ley conmutativa. De hecho, no lo satisface más bien espectacularmente.
Una generalización del siguiente resultado fue declarada y probada por Bernhard Riemann en 1854.
\(a\)Sea cualquier número real. Existe un reordenamiento de la serie\(1 - \frac{1}{2} + \frac{1}{3} - \cdots\) que converge a\(a\).
Este teorema muestra que una serie es decididamente no es una gran suma grande. De ello se deduce que una serie de potencias no es un gran polinomio grande.
Para establecer el escenario, considere la serie armónica
\[\sum_{n=1}^{\infty }\frac{1}{n} = 1 + \frac{1}{2} + \frac{1}{3} + \cdots\]
A pesar de que los términos individuales de esta serie convergen a\(0\), la serie aún diverge (hasta el infinito) como lo demuestra la desigualdad
\[\begin{align*} \left (1 + \frac{1}{2} \right ) + \left (\frac{1}{3} + \frac{1}{4} \right ) + \left (\frac{1}{5} + \frac{1}{6}+ \frac{1}{7} + \frac{1}{8} \right ) + \left (\frac{1}{9} + \cdots + \frac{1}{16} \right ) + \cdots & > \frac{1}{2} + \left (\frac{1}{4} + \frac{1}{4} \right ) + \left (\frac{1}{8} + \frac{1}{8}+ \frac{1}{8} + \frac{1}{8} \right ) + \left (\frac{1}{16} + \cdots + \frac{1}{16} \right ) + \cdots\\ &= \frac{1}{2} + \frac{1}{2} + \frac{1}{2} + \frac{1}{2} + \cdots \\ &= \infty \\ \end{align*}\]
Armados con este hecho, podemos ver por qué el Teorema\(\PageIndex{1}\) es cierto. Primero tenga en cuenta que
\[-\frac{1}{2} - \frac{1}{4} - \frac{1}{6} - \cdots = -\frac{1}{2}\left ( 1 + \frac{1}{2} + \frac{1}{3} + \cdots \right )= -\infty\]
y
\[1 + \frac{1}{3} + \frac{1}{5} + \cdots \geq \frac{1}{2} + \frac{1}{4} +\frac{1}{6} + \cdots = \infty\]
Esto dice que si agregamos suficientes términos de\(-\frac{1}{2} - \frac{1}{4} - \frac{1}{6} - \cdots\) podemos hacer una suma tan pequeña como queramos y si agregamos suficientes términos de\(1 + \frac{1}{3} + \frac{1}{5} + \cdots\) podemos hacer una suma tan grande como queramos. Esto nos proporciona el esquema general de la prueba. El truco es agregar los términos positivos suficientes hasta que la suma sea simplemente mayor que a. Luego comenzamos a sumar términos negativos hasta que la suma sea apenas menor que a. Retomando donde lo dejamos con los términos positivos, agregamos los términos positivos suficientes hasta que estemos justo por encima de una otra vez. Luego agregamos términos negativos hasta que estemos por debajo de a. en esencia, estamos rebotando de un lado a otro\(a\). Si hacemos esto con cuidado, entonces podemos lograr que este reordenamiento converja\(a\). La notación en la prueba a continuación se pone un poco peluda, pero ten en cuenta esta idea general mientras la lees.
Dejar\(O_1\) ser el primer entero impar tal que\(1 + \frac{1}{3} + \frac{1}{5} + \cdots +\frac{1}{O_1} > a\). Ahora elige\(E_1\) ser el primer número entero par de tal manera que
\[-\frac{1}{2} - \frac{1}{4} - \frac{1}{6} - \cdots - \frac{1}{E_1} < a - \left (1 + \frac{1}{3} + \frac{1}{5} + \cdots +\frac{1}{O_1} \right )\]
Así
\[1 + \frac{1}{3} + \frac{1}{5} + \cdots +\frac{1}{O_1} -\frac{1}{2} - \frac{1}{4} - \frac{1}{6} - \cdots - \frac{1}{E_1} < a\]
Observe que todavía tenemos\(\frac{1}{O_1+2} + \frac{1}{O_1+4} + \cdots = \infty\). Con esto en mente, elige\(O_2\) ser el primer entero impar con
\[\frac{1}{O_1+2} + \frac{1}{O_1+4} + \cdots + \frac{1}{O_2} > a - \left ( 1 + \frac{1}{3} + \frac{1}{5} + \cdots +\frac{1}{O_1} -\frac{1}{2} - \frac{1}{4} - \frac{1}{6} - \cdots - \frac{1}{E_1} \right )\]
Así tenemos
\[a < 1 + \frac{1}{3} + \frac{1}{5} + \cdots + \frac{1}{O_1} -\frac{1}{2} - \frac{1}{4} - \frac{1}{6} - \cdots - \frac{1}{E_1} + \frac{1}{O_1+2} + \frac{1}{O_1+4} + \cdots + \frac{1}{O_2}\]
Además, desde
\[1 + \frac{1}{3} + \frac{1}{5} + \cdots + \frac{1}{O_1} -\frac{1}{2} - \frac{1}{4} - \frac{1}{6} - \cdots - \frac{1}{E_1} + \frac{1}{O_1+2} + \frac{1}{O_1+4} + \cdots + \frac{1}{O_2 - 2} < a\]
tenemos
\[\left |1 + \frac{1}{3} + \frac{1}{5} + \cdots + \frac{1}{O_1} -\frac{1}{2} - \frac{1}{4} - \frac{1}{6} - \cdots - \frac{1}{E_1} + \frac{1}{O_1+2} + \frac{1}{O_1+4} + \cdots + \frac{1}{O_2} - a \right | < \frac{1}{O_2}\]
De manera similar opta por\(E_2\) ser el primer entero par de tal manera que
\[1 + \frac{1}{3} + \frac{1}{5} + \cdots + \frac{1}{O_1} -\frac{1}{2} - \frac{1}{4} - \frac{1}{6} - \cdots - \frac{1}{E_1} + \frac{1}{O_1+2} + \frac{1}{O_1+4} + \cdots + \frac{1}{O_2} - \frac{1}{E_1+2} - \frac{1}{E_1+4} - \cdots - \frac{1}{E_2} < a\]
Desde
\[1 + \frac{1}{3} + \frac{1}{5} + \cdots + \frac{1}{O_1} -\frac{1}{2} - \frac{1}{4} - \frac{1}{6} - \cdots - \frac{1}{E_1} + \frac{1}{O_1+2} + \frac{1}{O_1+4} + \cdots + \frac{1}{O_2} - \frac{1}{E_1+2} - \frac{1}{E_1+4} - \cdots - \frac{1}{E_2-2} > a\]
entonces
\[\left |1 + \frac{1}{3} + \frac{1}{5} + \cdots + \frac{1}{O_1} -\frac{1}{2} - \frac{1}{4} - \frac{1}{6} - \cdots - \frac{1}{E_1} + \frac{1}{O_1+2} + \frac{1}{O_1+4} + \cdots + \frac{1}{O_2} + \cdots - \frac{1}{E_1+2} - \frac{1}{E_1+4} - \cdots - \frac{1}{E_2} - a \right | < \frac{1}{E_2}\]
De nuevo elige\(O_3\) ser el primer entero impar de tal manera que
\[a < 1 + \frac{1}{3} + \frac{1}{5} + \cdots + \frac{1}{O_1} -\frac{1}{2} - \frac{1}{4} - \frac{1}{6} - \cdots - \frac{1}{E_1} + \frac{1}{O_1+2} + \frac{1}{O_1+4} + \cdots + \frac{1}{O_2} + \cdots - \frac{1}{E_1+2} - \frac{1}{E_1+4} - \cdots - \frac{1}{E_2} + \frac{1}{O_2+2} + \frac{1}{O_2+4} + \cdots + \frac{1}{O_3}\]
y fíjate que
\[\left | 1 + \frac{1}{3} + \frac{1}{5} + \cdots + \frac{1}{O_1} -\frac{1}{2} - \frac{1}{4} - \frac{1}{6} - \cdots - \frac{1}{E_1} + \frac{1}{O_1+2} + \frac{1}{O_1+4} + \cdots + \frac{1}{O_2} - \frac{1}{E_1+2} - \frac{1}{E_1+4} - \cdots - \frac{1}{E_2} + \frac{1}{O_2+2} + \frac{1}{O_2+4} + \cdots + \frac{1}{O_3} - a \right | < \frac{1}{O_3}\]
Continuar definiendo\(O_k\) y\(E_k\) de esta manera. Ya que\(\lim_{k \to \infty } \frac{1}{O_k} = \lim_{k \to \infty } \frac{1}{E_k} = 0\), es evidente que las sumas parciales
\[1 + \frac{1}{3} + \frac{1}{5} + \cdots + \frac{1}{O_1} -\frac{1}{2} - \frac{1}{4} - \frac{1}{6} - \cdots - \frac{1}{E_1} + \frac{1}{O_1+2} + \frac{1}{O_1+4} + \cdots + \frac{1}{O_2} + \cdots - \frac{1}{E_{k-2}+2} - \frac{1}{E_{k-2}+4} - \cdots - \frac{1}{E_{k-1}} + \frac{1}{O_{k-1}+2} + \frac{1}{O_{k-1}+4} + \cdots + \frac{1}{O_k}\]
y
\[1 + \frac{1}{3} + \frac{1}{5} + \cdots + \frac{1}{O_1} -\frac{1}{2} - \frac{1}{4} - \frac{1}{6} - \cdots - \frac{1}{E_1} + \frac{1}{O_1+2} + \frac{1}{O_1+4} + \cdots + \frac{1}{O_2} + \cdots\]
está atrapado entre dos sumas parciales tan extremas. Esto obliga a que toda la serie reordenada converja a\(a\).
Los siguientes dos problemas son similares a los anteriores, pero notacionalmente son más fáciles ya que no necesitamos preocuparnos por converger a un número real. Solo necesitamos hacer que el reordenamiento crezca (o se encoja) sin ataduras.
Demostrar que hay un reordenamiento del\(1 - \frac{1}{2} + \frac{1}{3} - \frac{1}{4} + \cdots\) cual diverge a\(∞\).
Demostrar que hay un reordenamiento del\(1 - \frac{1}{2} + \frac{1}{3} - \frac{1}{4} + \cdots\) cual diverge a\(-\infty\).
Es divertido saber que podemos reorganizar algunas series para que se sumen a lo que quieras pero aquí hay una idea más fundamental en juego. Que los términos negativos de la Serie Armónica alterna diverjan al infinito negativo y los términos positivos diverjan al infinito positivo hacen que la convergencia de las series alternas sea muy especial.
Consideremos, primero agregamos\(1\): Este es uno de los términos positivos por lo que nuestra suma empieza a aumentar sin ataduras. A continuación agregamos\(-1/2\) cual es uno de los términos negativos por lo que nuestra suma ha dado la vuelta y ahora empieza a disminuir sin ataduras. Entonces se agrega otro término positivo: aumentar sin ataduras. Luego otro término negativo: decreciente. Y así sucesivamente. La convergencia de la serie armónica alterna es el resultado de un delicado equilibrio entre una tendencia a correr hacia el infinito positivo y volver al infinito negativo. Cuando se ve bajo esta luz, en realidad no es demasiado sorprendente que reorganizar los términos pueda destruir este delicado equilibrio.
Naturalmente, la serie armónica alterna no es la única serie de este tipo. Se dice que cualquier serie de este tipo converge “condicionalmente” —siendo la condición la disposición específica de los términos.
Para revolver un poco más la olla, algunas series satisfacen la propiedad conmutativa. Más específicamente, se puede demostrar que cualquier reordenamiento de la serie\(1 - \frac{1}{2^2} + \frac{1}{3^2} - \cdots\) debe converger al mismo valor que la serie original (que pasa a ser\(\int_{x=0}^{1} \frac{\ln (1+x)}{x}dx \approx 0.8224670334\)). ¿Por qué una serie se comporta tan bien mientras que la otra no?
Temas como estos y, de manera más general, la validez de usar lo infinitamente pequeño e infinitamente grande ciertamente existieron en los años 1700, pero fueron eclipsados por la utilidad del cálculo. En efecto, las cuestiones fundacionales planteadas por los ejemplos anteriores, aunque ciertamente interesantes y de importancia, no disuadieron significativamente la explotación del cálculo en el estudio de los fenómenos físicos. Sin embargo, la envolvente finalmente fue empujada hasta el punto de que ni siquiera el matemático más orientado prácticamente pudo evitar los problemas fundacionales.

