5.3: La forma del resto de Cauchy

Objetivos de aprendizaje

• Explicar la forma de Cauchy del resto

En su obra de 1823, Résumé des lecons données à l'ecole royale polytechnique sur le calcul infintésimal, Augustin Cauchy proporcionó otra forma del resto para la serie Taylor.

Teorema\(\PageIndex{1}\): Cauchy’s Form of the Remainder

Supongamos que\(f\) es una función tal que\(f^{(n+1)}(t)\) es continua en un intervalo que contiene\(a\) y\(x\). Entonces

\[f(x) - \left ( \sum_{j=0}^{n}\dfrac{f^{(j)}(a)}{j!}(x-a)^j \right ) = \dfrac{f^{(n+1)}(c)}{n!}(x-c)^n(x-a)\]

donde\(c\) hay algún número entre\(a\) y\(x\).

Ejercicio\(\PageIndex{1}\)

Demostrar Teorema\(\PageIndex{1}\) utilizando un argumento similar al utilizado en la prueba del Teorema 5.2.1. No olvides que hay dos casos a considerar.

Usando la forma de Cauchy del resto, podemos probar que la serie binomial

\[1 + \dfrac{1}{2}x + \dfrac{\dfrac{1}{2}\left ( \dfrac{1}{2} -1 \right )}{2!}x^2 + \dfrac{\dfrac{1}{2}\left ( \dfrac{1}{2} -1 \right )\left ( \dfrac{1}{2} -2 \right )}{3!}x^3 + \cdots\]

converge a\(\sqrt{1+x}\) for\(x ∈ (-1,0)\). Con esto en mente, dejemos\(x\) ser un número fijo con\(-1 < x < 0\) y considerar que la serie binomial es la serie Maclaurin para la función\(f(x) = (1 + x)^\dfrac{1}{2}\). Como vimos antes,

\[f^{(n+1)}(t) = \left ( \dfrac{1}{2} \right )\left ( \dfrac{1}{2} -1 \right )\cdots \left ( \dfrac{1}{2} -n \right )(1+t)^{\dfrac{1}{2} - (n+1)}\]

por lo que la forma Cauchy del resto viene dada por

\[0 \leq \left | \dfrac{f^{(n+1)}(c)}{n!}(x-c)^n(x-0) \right | = \left | \dfrac{\dfrac{1}{2}\left ( \dfrac{1}{2} -1 \right )\cdots \left ( \dfrac{1}{2} -n \right )}{n!} \dfrac{(x-c)^n}{(1+c)^{n+\dfrac{1}{2}}}\cdot x\right |\]

donde\(c\) hay algún número con\(x ≤ c ≤ 0\). Así tenemos

\[\begin{align*} 0 &\leq \left | \dfrac{\left ( \dfrac{1}{2} \right )\left ( \dfrac{1}{2} -1 \right )\cdots \left ( \dfrac{1}{2} -n \right )}{n!} \dfrac{(x-c)^n x}{(1+c)^{n + \dfrac{1}{2}}} \right | \\ &= \dfrac{\left ( \dfrac{1}{2} \right )\left ( 1 -\dfrac{1}{2} \right )\cdots \left ( n - \dfrac{1}{2} \right )}{n!} \dfrac{\left |x-c \right |^n\left | x \right |}{(1+c)^{n + \dfrac{1}{2}}}\\ &= \dfrac{\left ( \dfrac{1}{2} \right )\left ( \dfrac{1}{2} \right )\left ( \dfrac{3}{2} \right )\left ( \dfrac{5}{2} \right )\cdots \left ( \dfrac{2n-1}{2} \right )}{n!})\dfrac{(c-x)^n}{(1+c)^n}\dfrac{\left |x \right |}{\sqrt{1+c}}\\ &\leq \dfrac{1\cdot 1\cdot 3\cdot 5\cdots (2n-1)}{2^{n+1}n!} \left (\dfrac{c-x}{1+c} \right )^n\dfrac{\left |x \right |}{\sqrt{1+c}}\\ &= \dfrac{1\cdot 1\cdot 3\cdot 5\cdot (2n-1)}{2\cdot 2\cdot 4\cdot 6\cdots 2n} \left (\dfrac{c-x}{1+c} \right )^n\dfrac{\left |x \right |}{\sqrt{1+c}}\\ &= \dfrac{1}{2} \cdot \dfrac{1}{2} \cdot \dfrac{3}{4} \cdot \dfrac{5}{6} \cdots \dfrac{2n-1}{2n}\cdot \left (\dfrac{c-x}{1+c} \right )^n\dfrac{\left |x \right |}{\sqrt{1+c}}\\ &\leq \left (\dfrac{c-x}{1+c} \right )^n\dfrac{\left |x \right |}{\sqrt{1+c}} \end{align*}\]

Observe que si\(-1 < x ≤ c\), entonces\(0 < 1 + x ≤ 1 + c\). Así\(0 < \dfrac{1}{1+c} \leq \dfrac{1}{1+x}\) y\(\dfrac{1}{\sqrt{1+c}} \leq \dfrac{1}{\sqrt{1+x}}\). Así tenemos

\[0 \leq \left |\dfrac{\left ( \dfrac{1}{2} \right )\left ( \dfrac{1}{2} -1 \right )\cdots \left ( \dfrac{1}{2} -n \right )}{n!} \dfrac{(x-c)^n x}{(1+c)^{n + \dfrac{1}{2}}} \right | \leq \left (\dfrac{c-x}{1+c} \right )^n\dfrac{\left |x \right |}{\sqrt{1+c}}\]

Ejercicio\(\PageIndex{2}\)

Supongamos\(-1 < x ≤ c ≤ 0\) y consideremos la función\(g(c) = \dfrac{c-x}{1+x}\). Demostrar que en\([x,0]\),\(g\) va en aumento y utilizar esto para concluir que para\(-1 < x ≤ c ≤ 0\),

\[\dfrac{c-x}{1+x} \leq \left | x \right | \nonumber\]

Utilice este hecho para terminar la prueba de que la serie binomial converge a\(\sqrt{1+x}\) for\(-1 < x < 0\).

Las pruebas tanto de la forma Lagrange como de la forma Cauchy del resto para la serie Taylor hicieron uso de dos hechos cruciales sobre las funciones continuas.

Primero, asumimos el Teorema del Valor Extremo: Cualquier función continua en un intervalo delimitado cerrado asume su máximo y mínimo en algún lugar del intervalo.

Segundo, asumimos que cualquier función continua satisfizo el Teorema del Valor Intermedio: Si una función continua toma dos valores diferentes, entonces debe tomar cualquier valor entre esos dos valores.

Figura\(\PageIndex{1}\): Augustin Cauchy

Los matemáticos a finales de 1700 y principios de 1800 generalmente consideraban que estos hechos eran intuitivamente obvios. Esto era natural ya que nuestra comprensión de la continuidad en ese momento era, únicamente, intuitiva. La intuición es una herramienta útil, pero como hemos visto antes también es poco confiable. Por ejemplo, considere la siguiente función.

\[f(x) = \begin{cases} x\sin \left (\dfrac{1}{x} \right ) & \text{ if } x \neq 0 \\ 0 & \text{ if } x= 0 \end{cases}\]

¿Esta función es continua en\(0\)? Cerca de cero su gráfica se ve así:

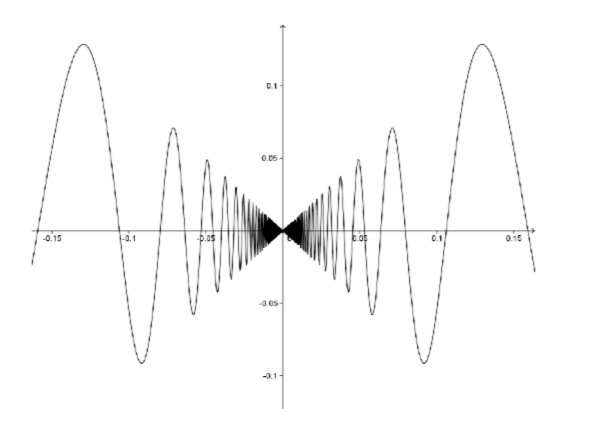
Figura\(\PageIndex{2}\): Gráfica de la función anterior.

pero esta gráfica debe tomarse con un grano de sal ya que\(\sin \left (\dfrac{1}{x} \right )\) oscila infinitamente a menudo a medida que se\(x\) acerca a cero. No importa cuál sea tu suposición, está claro que es difícil analizar tal función armada solo con una noción intuitiva de continuidad. Volveremos a visitar este ejemplo en el próximo capítulo.

Al igual que con la convergencia, la continuidad es más sutil de lo que parece al principio. Ponemos la convergencia en terreno sólido al proporcionar una definición completamente analítica en el capítulo anterior. Lo que tenemos que hacer en el siguiente capítulo es proporcionar una definición completamente rigurosa para la continuidad.