6.1: Una definición analítica de la continuidad
- Page ID
- 109428
- Explicar continuidad
Antes de la invención del cálculo, la noción de continuidad se trataba intuitivamente si se trataba en absoluto. Al primer paso, parece una idea muy sencilla basada sólidamente en nuestra experiencia del mundo real. De pie en la orilla vemos un río que fluye más allá de nosotros continuamente, no por pequeños idiotas. Incluso cuando el flujo pueda parecer al principio discontinuo, como cuando cae precipitadamente sobre un acantilado, un examen más detallado demuestra que realmente no lo es. A medida que el agua se acerca al acantilado se acelera. Cuando finalmente pasa por encima se acelera muy rápido pero por muy rápido que vaya, se mueve continuamente, moviéndose de aquí para allá ocupando cada punto intermedio. Esto es movimiento continuo. Nunca desaparece allá y reaparece instantáneamente por aquí. Eso sería movimiento discontinuo.
De manera similar, una piedra arrojada florece continuamente (y suavemente) desde el punto de liberación hasta el punto de aterrizaje, pasando por cada punto a su paso.
Pero espera. Si la piedra pasa por puntos discretos debe estar haciéndolo por pequeñitos idiotas, ¿no es así? De lo contrario, ¿cómo llegaría de un punto a otro? ¿Es posible que el movimiento en el mundo real, al igual que el movimiento en una película, esté realmente compuesto de pequeños tirones de un punto a otro pero que estos pequeños tirones son simplemente demasiado pequeños y demasiado rápidos para que nuestros sentidos los detecten?
Si es así, entonces el mundo real se parece más a la recta numérica racional (\(\mathbb{Q}\)) del Capítulo 1 que a la recta numérica real (\(\mathbb{R}\)). En ese caso, el movimiento consiste realmente en saltar discretamente sobre los puntos “faltantes” (como\(\sqrt{2}\)) a medida que nos movemos de aquí para allá. Eso puede parecerle una idea extraña —a nosotros también nos hace— pero la idea del movimiento continuo es igualmente extraña. Solo es un poco más difícil ver por qué.
El mundo real será lo que es independientemente de lo que creamos que es, pero afortunadamente en matemáticas no estamos obligados a vivir en él. Así que ni siquiera lo intentaremos. Simplemente vamos a postular que no existe tal sacudida; que todo movimiento es continuo.
Sin embargo, estamos obligados a vivir con las consecuencias lógicas de nuestros supuestos, una vez que se hacen. Estos nos conducirán a algunas aguas muy profundas en verdad.
El tratamiento intuitivo de la continuidad se mantuvo a lo largo de la década de 1700 ya que generalmente no se percibía que fuera necesaria una definición verdaderamente rigurosa. Considera la siguiente definición dada por Euler en 1748.
Una curva continua es aquella tal que su naturaleza puede ser expresada por una sola función de\(x\). Si una curva es de tal naturaleza que por sus diversas partes...\(x\) se requieren diferentes funciones de para su expresión,..., entonces llamamos a tal curva discontinua.
Sin embargo, las complejidades asociadas con las series de Fourier y los tipos de funciones que representaban provocaron que los matemáticos a principios de 1800 replantearan sus nociones de continuidad. Como vimos en la Parte II, la gráfica de la función definida por la serie de Fourier
\[\frac{4}{\pi }\sum_{k=0}^{\infty } \frac{(-1)^k}{(2k+1)} \cos ((2k+1)\pi x)\]
se veía así:
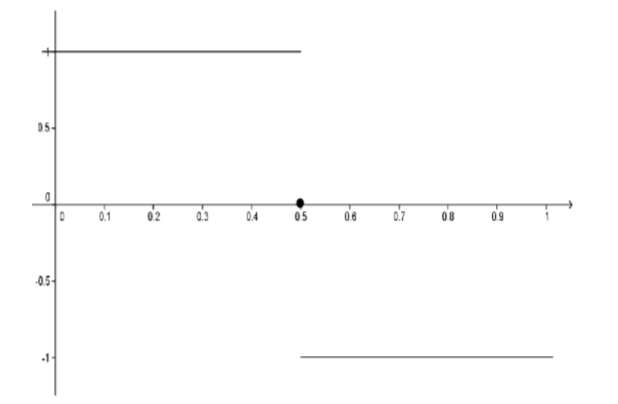
Figura\(\PageIndex{1}\): Gráfico de función definida por la serie de Fourier.
Esta función iba en contra de la noción de Euler de lo que debería ser una función continua. Aquí, una suma infinita de curvas continuas de coseno proporcionó una sola expresión que resultó en una curva “discontinua”. Pero como hemos visto esto no sucedió con las series de poder y una noción intuitiva de continuidad es inadecuada para explicar la diferencia. Aún más desplejo es la siguiente situación. Intuitivamente, uno pensaría que una curva continua debe tener una línea tangente en al menos un punto. Puede tener una serie de puntos dentados, pero debería ser “suave” en alguna parte. Un ejemplo de ello sería\(f(x) = x^{2/3}\). Su gráfica viene dada por
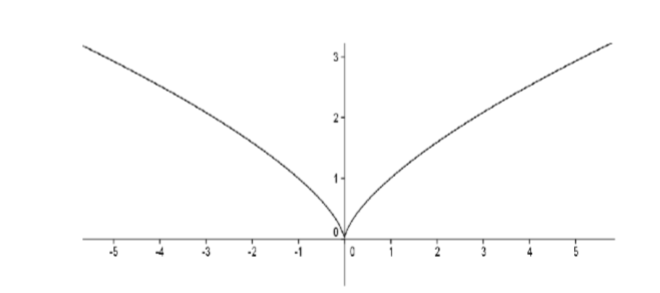
Figura\(\PageIndex{2}\): Gráfica de\(f(x) = x^{2/3}\).
Esta función no es diferenciable en el origen pero es diferenciable en todas partes. Ciertamente se podrían llegar a ejemplos de funciones que no logran ser diferenciables en ningún número de puntos pero, intuitivamente, sería razonable esperar que una función continua sea diferenciable en alguna parte. Podríamos conjeturar lo siguiente:
Si f es continuo en un intervalo\(I\) entonces hay algo\(a ∈ I\), tal que\(f'(a)\) existe.

Figura\(\PageIndex{3}\): Karl Weierstrass.
Sorprendentemente, en 1872, Karl Weierstrass demostró que la conjetura anterior es FALSA. Lo hizo mostrando el contraejemplo:
\[f(x) = \sum_{n=0}^{\infty }b^n\cos (a^n\pi x)\]
Weierstrass demostró que si\(a\) es un entero impar,, y\(b ∈ (0,1)\)\(ab > 1 + \frac{3}{2}π\), entonces\(f\) es continuo en todas partes, pero no es en ninguna parte diferenciable. Tal función es algo “fractal” por naturaleza, y es evidente que una definición de continuidad basada en la intuición es inadecuada para estudiarla.
- Dado\(f(x) = \sum_{n=0}^{\infty }\left ( \frac{1}{2} \right )^n\cos (a^n\pi x)\), cuál es el valor más pequeño\(a\) para el cual\(f\) satisface el criterio de Weierstrass de ser continuo y en ninguna parte diferenciable.
- Dejar\(f(x,N) = \sum_{n=0}^{N}\left ( \frac{1}{2} \right )^n\cos (13^n\pi x)\) y usar un sistema de álgebra computacional\(f(x,N)\) para trazar para\(N = 0,1,2,3,4,10\) y\(x ∈ [0,1]\).
- Parcela\(f(x,10)\) para\(x ∈ [0,c]\), donde\(c = 0.1,0.01,0.001,0.0001,0.00001\). Con base en lo que se ve en las partes b y c, ¿por qué describiríamos la función como algo “fractal” por naturaleza?
Así como era importante definir la convergencia con una definición rigurosa sin apelar a la intuición o a las representaciones geométricas, es imperativo que definamos la continuidad de manera rigurosa sin depender de las gráficas.
La primera aparición de una definición de continuidad que no se basaba en la geometría o la intuición fue dada en 1817 por Bernhard Bolzano en un artículo publicado en las Actas de la Sociedad Científica de Praga titulado
Rein analytischer Beweis des Lehrsatzes dass zwieschen je zwey Werthen, die ein entgegengesetztes Resultat gewaehren, wenigstens eine reele Wurzel der Gleichung liege (Prueba puramente analítica del teorema de que entre dos valores cualesquiera que arrojan resultados de signo opuesto habrá al menos un real Raíz de la Ecuación).

Figura\(\PageIndex{4}\): Bernhard Bolzano
Del título debe quedar claro que en este trabajo Bolzano está probando el Teorema del Valor Intermedio. Para ello necesita una definición completamente analítica de continuidad. El fondo de la idea de Bolzano es que si\(f\) es continuo en un punto a entonces\(f(x)\) debería estar “cerca”\(f(a)\) siempre que\(x\) esté “lo suficientemente cerca de”\(a\). Más precisamente, Bolzano dijo que\(f\) es continuo a un proporcionado se\(|f(x) - f(a)|\) puede hacer más pequeño que cualquier cantidad dada siempre que hagamos\(|x - a|\) suficientemente pequeña.
El lenguaje que utiliza Bolzano es muy similar al lenguaje que Leibniz utilizó cuando postuló la existencia de números infinitesimalmente pequeños. Leibniz dijo que los infinitesimales son “más pequeños que cualquier cantidad dada pero no cero. ” Bolzano dice que “se\(|f(x) - f(a)|\) puede hacer más pequeño que cualquier cantidad dada siempre que hagamos\(|x - a|\) lo suficientemente pequeña. ” Pero Bolzano no llega a decir que\(|x - a|\) es infinitesimalmente pequeño. Dado un, podemos elegir\(x\) para que\(|x - a|\) sea más pequeño que cualquier número real que pudiéramos nombrar, digamos\(b\), siempre que nombremos\(b\) primero, pero para cualquier elección dada de\(x\),\(|x - a|\), y ambos\(b\) siguen siendo números reales. Posiblemente números reales muy pequeños para estar seguros, pero números reales no obstante. Los infinitesimales no tienen cabida en la construcción de Bolzano.
El artículo de Bolzano no era muy conocido cuando Cauchy propuso una definición similar en su Cours d'analyse [1] de 1821 por lo que suele ser Cauchy quien se le atribuye esta definición, pero incluso la definición de Cauchy no es lo suficientemente ajustada para los estándares modernos. Fue Karl Weierstrass en 1859 quien finalmente dio la definición moderna.
Decimos que una función\(f\) es continua a\(a\) condición de que para cualquiera\(ε > 0\), exista\(a δ > 0\) tal que si\(|x - a| < δ\) entonces\(|f(x) - f(a)| < ε\).
Observe que la definición de continuidad de una función se realiza punto por punto. Una función ciertamente puede ser continua en algunos puntos mientras que discontinua en otros. Cuando decimos que\(f\) es continuo en un intervalo, entonces queremos decir que es continuo en cada punto de ese intervalo y, en teoría, necesitaríamos usar la definición anterior para verificar la continuidad en cada punto individual.
Nuestra definición encaja en el proyecto de ley en que no se basa ni en la intuición ni en los gráficos, sino que es esta misma no intuición la que hace que sea difícil de entender. Por lo general, lleva algún tiempo sentirse cómodo con esta definición, y mucho menos utilizarla para probar teoremas como el Teorema del Valor Extremo y el Teorema del Valor Intermedio. Así que vayamos despacio para desarrollar una sensación por ello.
Esta definición deletrea un procedimiento completamente en blanco y negro: me das un número positivo\(ε\), y debo poder encontrar un número positivo\(δ\) que satisfaga una determinada propiedad. Si siempre puedo hacer eso entonces la función es continua en el punto de interés.
Esta definición también hace muy preciso lo que queremos decir cuando decimos que\(f(x)\) debe estar “cerca de”\(f(a)\) siempre que\(x\) esté “lo suficientemente cerca de”\(a\). Por ejemplo, intuitivamente sabemos que\(f(x) = x^2\) debe ser continuo en\(x = 2\). Esto significa que deberíamos poder llegar\(x^2\) a dentro, digamos,\(ε = 0.1\) de\(4\) siempre que nos\(x\) acerquemos lo suficiente a\(2\). Específicamente, queremos\(3.9 < x^2 < 4.1\). Esto sucede exactamente cuando\(\sqrt{3.9} < x < \sqrt{4.1}\). Usando el hecho de que\(\sqrt{3.9} < 1.98\) y\(2.02 < \sqrt{4.1}\), entonces podemos ver que si llegamos\(x\) a dentro\(δ = 0.02\) de\(2\), entonces\(\sqrt{3.9} < 1.98 < x < 2.02 < \sqrt{4.1}\) y así\(x^2\) será dentro\(0.1\) de\(4\). Esto es muy sencillo. Lo que dificulta esta situación es que debemos ser capaces de hacer esto por cualquiera\(ε > 0\).
Observe la similitud entre esta definición y la definición de convergencia de una secuencia. Ambas definiciones tienen el reto de un\(ε > 0\). En la definición de\(\lim_{n \to \infty }s_n = s\), teníamos que llegar\(s_n\) al interior\(ε\) de\(s\) haciendo lo suficientemente\(n\) grande. Para las secuencias, el reto radica en hacer\(|s_n - s|\) suficientemente pequeñas. Más precisamente, dado\(ε > 0\) que necesitamos decidir qué tan grande\(n\) debe ser para garantizarlo\(|s_n - s| < ε\).
En nuestra definición de continuidad, todavía necesitamos hacer algo pequeño (es decir\(|f(x) - f(a)| < ε\)), solo que esta vez, necesitamos determinar qué tan cerca\(x\) debe estar de una para asegurar que esto suceda en lugar de determinar qué tan grande\(n\) debe ser.
Lo que hace\(f\) continuo en\(a\) es la naturaleza arbitraria de\(ε\) (siempre y cuando sea positiva). A medida que\(ε\) se hace más pequeño, esto obliga\(f(x)\) a estar más cerca de\(f(a)\). Que siempre podamos encontrar una distancia positiva\(δ\) para trabajar es a lo que nos referimos cuando decimos que podemos acercarnos\(f(x)\) lo más cerca que deseemos, siempre que nos\(x\) acerquemos lo suficiente\(a\).\(f(a)\) La secuencia de imágenes a continuación ilustra que la frase “para cualquiera\(ε > 0\), existe\(δ > 0\) tal que si\(|x - a| < δ\) entonces\(|f(x) - f(a)| < ε\)” puede ser reemplazada por la formulación equivalente “para cualquiera\(ε > 0\), existe\(δ > 0\) tal que si\(a - δ < x < a + δ\) entonces \(f(a) - ε < f(x) < f(a) + ε\).” Esto también podría sustituirse por la frase “para cualquiera\(ε > 0\), existe\(δ > 0\) tal que si\(x ∈ (a - δ,a + δ)\) entonces\(f(x) ∈ (f(a) - ε,f(a) + ε\)). ” Todas estas formulaciones equivalentes transmiten la idea de que podemos\(f(x)\) llegar dentro\(ε\) de\(f(a)\), siempre que hagamos\(x\) dentro\(δ\) de\(a\), y usaremos la formulación que se adapte a nuestras necesidades en una aplicación particular.
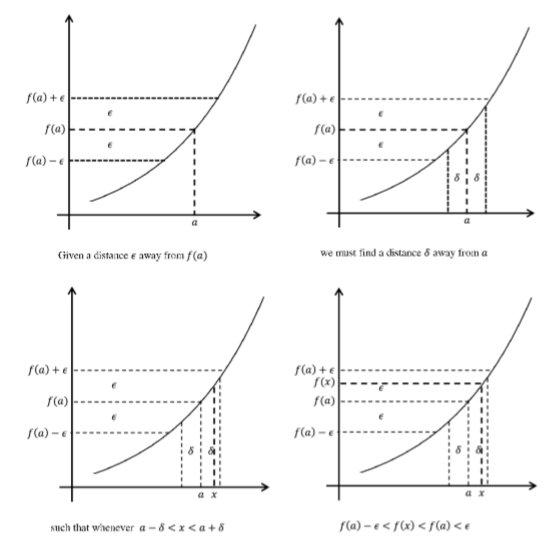
Figura\(\PageIndex{5}\): La función\(f\) es continua en\(a\).
La precisión de la definición es lo que nos permite examinar la continuidad sin depender de imágenes o nociones vagas como “cercanía” o “acercarnos”. Consideraremos ahora algunos ejemplos para ilustrar esta precisión.
Usa la definición de continuidad para mostrar que\(f(x) = x\) es continuo en cualquier punto\(a\).
Si tuviéramos que dibujar la gráfica de esta línea, entonces probablemente dirías que esto es obvio. El punto detrás de la definición es que podemos respaldar tu intuición de manera rigurosa.
Prueba:
Vamos\(ε > 0\). Vamos\(δ = ε\). Si\(|x - a| < δ\), entonces
\[|f(x) - f(a)| = |x - a| < ε\]
Así por la definición,\(f\) es continuo en\(a\).
Usa la definición de continuidad para mostrar que si\(m\) y\(b\) son números reales fijos (pero no especificados) entonces la función\(f(x) = mx + b\) es continua en cada número real\(a\).
Utilice la definición de continuidad para mostrar que\(f(x) = x^2\) es continuo en\(a = 0\).
Prueba:
Vamos\(ε > 0\). Vamos\(\delta = \sqrt{\varepsilon }\). Si\(|x - 0| < δ\), entonces\(\left | x \right |=\sqrt{\varepsilon }\). Así
\[\left | x^2 - 0^2 \right | = \left | x \right |^2 < (\sqrt{\varepsilon })^2 = \varepsilon\]
Así por la definición,\(f\) es continuo en\(0\).
Observe que en estas pruebas, primero\(ε > 0\) se dio el reto de un. Esto se debe a que la elección de\(δ\) debe depender\(ε\). También observe que no hubo explicación para nuestra elección de\(δ\). Acabamos de suministrarlo y demostramos que funcionaba. Siempre y cuando\(δ > 0\), entonces esto es todo lo que se requiere. De hecho, el\(δ\) que elegimos en cada ejemplo no fue la única opción que funcionó; cualquier menor\(δ\) funcionaría también.
- Dado un particular\(ε > 0\) en la definición de continuidad, mostrar que si un particular\(δ_0 > 0\) satisface la definición, entonces cualquiera\(δ\) con también\(0 < δ < δ_0\) funcionará para esto\(ε\).
- Demostrar que si a se\(δ\) puede encontrar que satisface las condiciones de la definición de continuidad para un particular\(ε_0 > 0\), entonces esto también\(δ\) funcionará para cualquiera\(ε\) con\(0 < ε_0 < ε\).
No se decía explícitamente en la definición pero cuando decimos “si\(|x - a| < δ\) entonces”\(|f(x) - f(a)| < ε\), deberíamos estar restringiéndonos a\(x\) valores que están en el dominio de la función\(f\), de lo contrario\(f(x)\) no tiene sentido. No lo pusimos en la definición porque esa definición era lo suficientemente complicada sin este tecnicismo. También en los ejemplos anteriores, las funciones se definieron en todas partes por lo que este fue un punto discutible. Continuaremos con la convención de que cuando digamos “si\(|x - a| < δ\) entonces”\(|f(x) - f(a)| < ε\), nos estaremos limitando a\(x\) valores que están en el dominio de la función\(f\). Esto nos permitirá examinar la continuidad de funciones no definidas para todos\(x\) sin replantear esta restricción cada vez.
Usa la definición de continuidad para demostrar que
\[f(x) = \begin{cases} \sqrt{x} & \text{ if } x \geq 0 \\ -\sqrt{-x} & \text{ if } x < 0 \end{cases}\]
es continuo en\(a = 0\).
Usa la definición de continuidad para mostrar que\ f (x) =\ sqrt {x}\) es continuo en\(a = 0\). ¿En qué se diferencia este problema del problema\(\PageIndex{4}\)? ¿Cómo es similar?
A veces lo\(δ\) que va a funcionar para un particular\(ε\) es bastante obvio de ver, especialmente después de haber adquirido algo de experiencia. Este es el caso en los ejemplos anteriores (al menos después de mirar hacia atrás en las pruebas). No obstante, la tarea de\(δ\) encontrar un trabajo no suele ser tan obvia y requiere algunos recortes. Este trabajo de recortes es vital para producir una\(δ\), pero de nuevo no forma parte de la prueba pulida. Esto se puede ver en el siguiente ejemplo.
Utilizar la definición de continuidad para demostrar que\(f(x) = \sqrt{x}\) es continua en\(a = 1\).
Scrapwork:
Como antes, el scrapwork para estos problemas suele consistir en simplemente trabajar al revés. Específicamente, dado un\(ε > 0\), necesitamos encontrar un para\(δ > 0\) que\(\left |\sqrt{x} - \sqrt{1} \right | < \varepsilon\), cuando sea\(|x - 1| < δ\). Trabajamos hacia atrás desde lo que queremos, vigilando el hecho de que podemos controlar el tamaño de\(|x - 1|\).
\[\left |\sqrt{x} - \sqrt{1} \right | = \left | \frac{(\sqrt{x}-1)(\sqrt{x}+1)}{\sqrt{x}+1} \right | = \frac{\left | x-1 \right |}{\sqrt{x}+1} < \left | x-1 \right |\]
Esto parece sugerir que debemos hacer\(δ = ε\). Ya estamos listos para la prueba formal.
Fin de Scrapwork
Prueba:
Vamos\(ε > 0\). Vamos\(δ = ε\). Si\(|x - 1| < δ\), entonces\(|x - 1| < ε\), y así
\[\left |\sqrt{x} - \sqrt{1} \right | = \left | \frac{(\sqrt{x}-1)(\sqrt{x}+1)}{\sqrt{x}+1} \right | = \frac{\left | x-1 \right |}{\sqrt{x}+1} < \left | x-1 \right | < \varepsilon\]
Así por definición,\(f(x) = \sqrt{x}\) es continuo en\(1\).
Ten en cuenta que alguien que lea la prueba formal no habrá visto el scrapwork, por lo que la elección de\(δ\) podría parecer bastante misteriosa. No obstante, de ninguna manera está obligado a motivar esta elección de\(δ\) y por lo general no debe hacerlo, a menos que sea necesario para la prueba formal. Todo lo que tienes que hacer es encontrar esto\(δ\) y demostrar que funciona. Además, a un lector capacitado, tus ideas llegarán a través cuando demuestres que tu elección de\(δ\) obras.
Ahora revertir esta última afirmación. Como lector capacitado, cuando lees la prueba de un teorema es tu responsabilidad encontrar el scrapwork, ver cómo funciona la prueba y entenderlo completamente.

Figura\(\PageIndex{6}\): Paul Halmos.
Como dijo el reconocido expositor matemático Paul Halmos (1916-2006),
No solo la leas; ¡lucha contra ella! Haz tus propias preguntas, busca tus propios ejemplos, descubre tus propias pruebas. ¿Es necesaria la hipótesis? ¿Es cierto lo contrario? ¿Qué sucede en el caso especial clásico? ¿Y los casos degenerados? ¿Dónde utiliza la prueba la hipótesis?
Esta es la manera de aprender matemáticas. Realmente es la única manera.
Utilice la definición de continuidad para mostrar que\(f(x) = \sqrt{x}\) es continuo en cualquier número real positivo\(a\).
- Use un círculo unitario para mostrar eso para\(0 \leq \theta < \frac{\pi }{2}\),\(\sin \theta \leq \theta\)\((1 - \cos \theta) \leq \theta\) y concluir\(|\sinθ|≤|θ|\) y\(|1-cosθ|≤|θ|\) para\(-\frac{\pi }{2} < \theta < \frac{\pi }{2}\).
- Utilizar la definición de continuidad para demostrar que\(f(x) = \sin x\) es continua en cualquier momento\(a\).
- Pista para (b)
-
\(\sin x = \sin(x - a + a)\)
- Utilice la definición de continuidad para mostrar que\(f(x) = e^x\) es continuo en\(a = 0\).
- Demostrar que\(f(x) = e^x\) es continuo en cualquier punto\(a\).
- Pista para (b)
-
Reescribe\(e^x - e^a\) as \(e^{a+(x-a)} - e^a\) y usa lo que probaste en la parte a
En los problemas anteriores, utilizamos la definición de continuidad para verificar nuestra intuición sobre la continuidad de las funciones familiares. La ventaja de esta definición analítica es que se puede aplicar cuando la función no es tan intuitiva. Consideremos, por ejemplo, la función dada al final del último capítulo.
\[f(x) = \begin{cases} x\sin \left (\frac{1}{x} \right ) & \text{ if } x \neq 0 \\ 0 & \text{ if } x= 0 \end{cases}\]
Cerca de cero, la gráfica de\(f(x)\) se ve así:
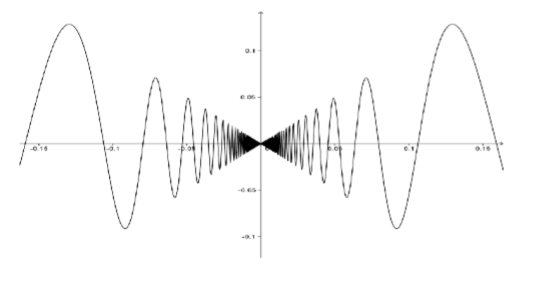
Figura\(\PageIndex{7}\): T la gráfica de\(f(x)\).
Como mencionamos en el capítulo anterior, ya que\(\sin \left (\frac{1}{x} \right )\) oscila infinitamente a menudo a medida que se\(x\) acerca a cero esta gráfica debe ser vista con cierta cantidad de sospecha. Sin embargo, nuestra definición completamente analítica de continuidad muestra que esta función es, de hecho, continua en\(0\).
Utilice la definición de continuidad para mostrar que\(f(x) = \begin{cases} x\sin \left (\frac{1}{x} \right ) & \text{ if } x \neq 0 \\ 0 & \text{ if } x= 0 \end{cases}\) es continuo en\(0\).
Aún más desplejo es la función definida por
\[D(x) = \begin{cases} x & \text{ if x is rational } \\ 0 & \text{ if x is irrational } \end{cases}\]
A simple vista, la gráfica de esta función se parece a las líneas\(y = 0\) y\(y = x\). Por supuesto, tal gráfica no sería la gráfica de una función. En realidad, ambas líneas tienen agujeros en ellas. Dondequiera que haya un punto en una línea hay un “agujero” en la otra. Cada uno de estos agujeros tiene el ancho de un solo punto (es decir, ¡su “ancho” es cero!) por lo que son invisibles a simple vista (o incluso magnificadas bajo el microscopio más potente disponible). Esta idea se ilustra en la siguiente gráfica
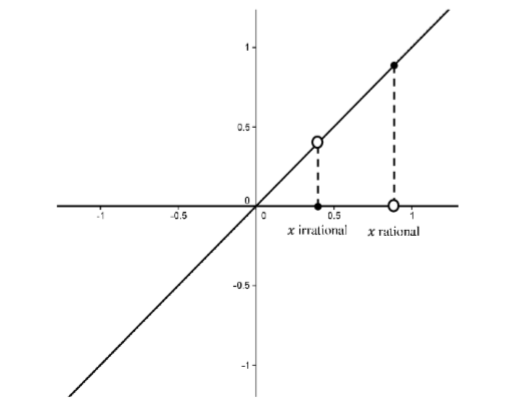
Figura\(\PageIndex{8}\): G rap h de la función\(D(x)\) como se definió anteriormente.
¿Puede tal función tan “llena de agujeros” ser realmente continua en cualquier lugar? Resulta que podemos usar nuestra definición para demostrar que esta función es, de hecho, continua en\(0\) y en ningún otro punto.
- Utilice la definición de continuidad para mostrar que la función\(D(x) = \begin{cases} x & \text{ if x is rational } \\ 0 & \text{ if x is irrational } \end{cases}\) es continua en\(0\).
- Vamos\(a \neq 0\). Utilice la definición de continuidad para mostrar que no\(D\) es continuo en\(a\).
- Sugerencia para (b)
-
Quizás quieras romper esto en dos casos en los que a es racional o irracional. Demuestre que no hay elección de\(δ > 0 \)will work for \(ε = |a|\). Note that Theorem 1.1.2 of Chapter 1 will probably help here.

