6.2: Secuencias y continuidad
- Page ID
- 109429
- Explicación adicional de secuencias y continuidad
Hay una forma alternativa de demostrar que la función
\[D(x) = \begin{cases} x & \text{ if x is rational } \\ 0 & \text{ if x is irrational } \end{cases}\]
no es continuo en\(a \neq 0\). Lo examinaremos analizando la relación entre nuestras definiciones de convergencia y continuidad. Las dos ideas están realmente muy estrechamente conectadas, como lo ilustra el siguiente teorema muy útil.
La función\(f\) es continua en\(a\) si y solo si\(f\) satisface la siguiente propiedad:
\[\forall \textit{ sequences} (x_n), \textit{ if } \lim_{n \to \infty }x_n = a \textit{ then } \lim_{n \to \infty }f(x_n) = f(a)\]
Teorema\(\PageIndex{1}\) dice que\(f\) para que sea continuo, es necesario y suficiente que cualquier secuencia (\(x_n\)) que converja a un debe forzar a la secuencia (\(f(x_n)\)) a converger a\(f(a)\). A continuación se muestra una imagen de esta situación, aunque, como siempre, la prueba formal no se basará en el diagrama.
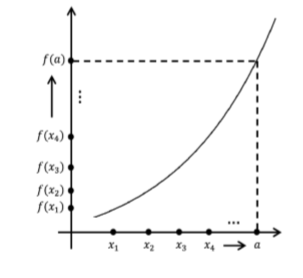
Figura\(\PageIndex{1}\): Una imagen de la situación descrita en Teorema\(\PageIndex{1}\).
Este teorema es especialmente útil para demostrar que una función no\(f\) es continua en un punto\(a\); todo lo que necesitamos hacer es exhibir una secuencia (\(x_n\)) convergente a una tal que la secuencia\(\displaystyle \lim_{n \to \infty }f(x_n)\) no converja a\(f(a)\). Demostremos esta idea antes de abordar la prueba del Teorema\(\PageIndex{1}\).
Utilice el teorema\(\PageIndex{1}\) para demostrar que
\[f(x) = \begin{cases} \frac{\left | x \right |}{x} & \text{ if } x\neq 0 \\ 0 & \text{ if } x= 0 \end{cases} \nonumber\]
no es continuo en\(0\).
Prueba:
Primer aviso que\(f\) se puede escribir como
\[f(x) = \begin{cases} 1 & \text{ if } x > 0 \\ -1 & \text{ if } x < 0 \\ 0 & \text{ if } x= 0 \end{cases} \nonumber\]
Para demostrar que no\(f\) es continuo en\(0\), todo lo que necesitamos hacer es crear una sola secuencia (\(x_n\)) que converja a\(0\), pero para la cual la secuencia (\(f(x_n)\)) no converge a\(f(0) = 0\). Para una función como esta, casi cualquier secuencia servirá, pero vamos a usar\(\left (\frac{1}{n} \right )\), solo porque es un viejo amigo familiar.
Tenemos
\[\lim_{n \to \infty }\frac{1}{n} = 0 \nonumber\]
pero
\[\lim_{n \to \infty }f \left (\frac{1}{n} \right ) = \lim_{n \to \infty }1 = 1 \neq 0 =f(0). \nonumber\]
Así por Teorema\(\PageIndex{1}\), no\(f\) es continuo en\(0\).
Usa el teorema\(\PageIndex{1}\) para demostrar que
\[f(x) = \begin{cases} \frac{\left | x \right |}{x} & \text{ if } x\neq 0 \\ a & \text{ if } x= 0 \end{cases} \nonumber\]
no es continuo en\(0\), no importa cuál\(a\) sea el valor.
Usa el teorema\(\PageIndex{1}\) para demostrar que
\[D(x) = \begin{cases} x & \text{ if x is rational } \\ 0 & \text{ if x is irrational } \end{cases} \nonumber\]
no es continuo en\(a \neq = 0\).
La función a menudo\(T(x) = \sin \left ( \frac{1}{x} \right )\) se llama curva sinusoidal del topólogo. Mientras que\(\sin x\) tiene raíces en\(nπ\),\(n ∈ \mathbb{Z}\) y oscila infinitamente a menudo como\(x \to \pm \infty\),\(T\) tiene raíces en\(\frac{1}{n\pi }\),,\(n ∈ \mathbb{Z}\)\(n \neq 0\), y oscila infinitamente a menudo a medida que se\(x\) acerca a cero. A continuación se muestra una versión de la gráfica.
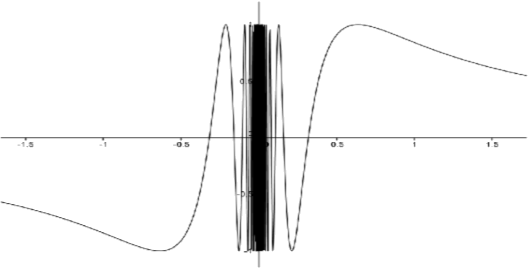
Figura\(\PageIndex{2}\): Gráfica de\(T(x)\) como se definió anteriormente.
Observe que ni siquiera\(T\) se define en\(x = 0\). Podemos extender\(T\) para ser definidos en simplemente\(0\) eligiendo un valor para\(T(0)\):
\[T(x) = \begin{cases} \sin \left ( \frac{1}{x} \right ) & \text{ if } x \neq 0 \\ b & \text{ if } x= 0 \end{cases} \nonumber\]
Usa el Teorema\(\PageIndex{1}\) para mostrar que no\(T\) es continuo en\(0\), sin importar para qué valor se elija\(b\).
Croquis de Prueba:
Hemos visto cómo podemos usar el Teorema\(\PageIndex{1}\), ahora necesitamos probar el Teorema\(\PageIndex{1}\). La dirección hacia adelante es bastante sencilla. Entonces asumimos que\(f\) es continuo en\(a\) y comenzamos con una secuencia (\(x_n\)) que converge a\(a\). Lo que queda por mostrar es eso\(\lim_{n \to \infty }f(x_n) = f(a)\). Si escribes las definiciones de\(f\) ser continuo en\(a\)\(\lim_{n \to \infty }x_n = a\),, y\(\lim_{n \to \infty }f(x_n) = f(a)\), deberías poder obtener de lo que estás asumiendo a lo que quieres concluir.
Para probar lo contrario, es conveniente demostrar su contrapositivo. Es decir, queremos probar que si no\(f\) es continuo en\(a\) entonces podemos construir una secuencia (\(x_n\)) que converja a\(a\) pero (\(f(x_n)\)) no converge a\(f(a)\). Primero tenemos que reconocer lo que significa\(f\) para no ser continuo en\(a\). Esto dice que en algún lugar existe una\(ε > 0\), tal que ninguna elección de\(δ > 0\) va a funcionar para esto. Es decir, para cualquiera de tales\(δ\), existirá\(x\), tal que\(|x-a| < δ\), pero\(|f(x)-f(a)|≥ ε\). Con esto en mente, si\(δ = 1\), entonces existirá\(x_1\) tal que\(|x_1 - a| < 1\), pero\(|f(x_1) - f(a)| ≥ ε\). Del mismo modo\(δ = \frac{1}{2}\), si, entonces existirá\(x_2\) tal que\(|x_2 - a| < \frac{1}{2}\), pero\(|f(x_2) - f(a)| ≥ ε\). Si seguimos de esta manera, vamos a crear una secuencia (\(x_n\)) tal que\(|x_n - a| < \frac{1}{n}\), pero\(|f(x_n) - f(a)|≥ ε\). Esto debería hacer el truco.
Convertir las ideas de los dos párrafos anteriores en una prueba formal del Teorema\(\PageIndex{1}\).
El teorema\(\PageIndex{1}\) es un resultado muy útil. Es un puente entre las ideas de convergencia y continuidad por lo que nos permite llevar toda la teoría que desarrollamos en el Capítulo 4 a incidir sobre cuestiones de continuidad. Por ejemplo, considera lo siguiente.
Supongamos\(f\) y ambos\(g\) son continuos en\(a\). Entonces\(f + g\) y\(f \cdot g\) son continuos en\(a\).
Podríamos usar la definición de continuidad para probar el Teorema\(\PageIndex{2}\), pero el Teorema\(\PageIndex{1}\) facilita mucho nuestro trabajo. Por ejemplo, para mostrar que\(f + g\) es continuo, considere cualquier secuencia (\(x_n\)) a la que converja\(a\). Ya que\(f\) es continuo en\(a\), entonces por Teorema\(\PageIndex{1}\),\(\lim_{n \to \infty }f(x_n) = f(a)\). De igual manera, ya que\(g\) es continuo en\(a\), entonces\(\lim_{n \to \infty }g(x_n) =g (a)\). Por Teorema 4.2.1 del Capítulo 4,\(\lim_{n \to \infty }(f + g)(x_n) = \lim_{n \to \infty }\left (f(x_n) + g(x_n) \right ) = \lim_{n \to \infty }f(x_n) + \lim_{n \to \infty }g(x_n) = f(a) + g(a) = (f+g)(a)\). Así por Teorema\(\PageIndex{1}\),\(f + g\) es continuo en\(a\). La prueba que\(f \cdot g\) es continua a una es similar.
Utilice el Teorema\(\PageIndex{1}\) para mostrar que si\(f\) y\(g\) son continuos en\(a\), entonces\(f \cdot g\) es continuo en\(a\).
Al emplear el Teorema\(\PageIndex{2}\) un número finito de veces, podemos ver que una suma finita de funciones continuas es continua. Es decir, si todos\(f_1, f_2, ..., f_n\) son continuos en\(a\) entonces\(\sum_{j=1}^{n} f_j\) es continuo en\(a\). Pero, ¿qué pasa con una suma infinita? Específicamente, supongamos que todos\(f_1, f_2, f_3,...\) son continuos en\(a\). Considera el siguiente argumento.
Vamos\(ε > 0\). Ya que\(f_j\) es continuo en\(a\), entonces existe\(δ_j > 0\) tal que si\(|x - a| < δ_j\), entonces\(|f_j(x) - f_j(a)| < \frac{ε}{2^j}\). Vamos\(δ = \min (δ_1, δ_2, ...)\). Si\(|x - a| < δ\), entonces
\[\left | \sum_{j=1}^{\infty } f_j(x) - \sum_{j=1}^{\infty } f_j(a) \right | = \left | \sum_{j=1}^{\infty } \left (f_j(x) - f_j(a) \right ) \right | \leq \sum_{j=1}^{\infty }\left | (f_j(x) - f_j(a) \right | < \sum_{j=1}^{\infty } \frac{\varepsilon }{2^j} = \varepsilon\]
Así, por definición,\(\sum_{j=1}^{\infty } f_j\) es continuo en\(a\).
Este argumento parece decir que una suma infinita de funciones continuas debe ser continua (siempre que converja). Sin embargo sabemos que la serie de Fourier
\[\frac{4}{\pi }\sum_{k=0}^{\infty } \frac{(-1)^k}{(2k+1)} \cos \left ( (2k+1)\pi x \right )\]
es un contraejemplo a esto, ya que es una suma infinita de funciones continuas que no converge a una función continua. Algo fundamental parece haber salido mal aquí. ¿Se puede decir qué es?
Esta es una pregunta que dedicaremos un tiempo considerable a abordar en el Capítulo 8 así que si no ves la dificultad, no te preocupes; lo harás. Mientras tanto mantén este problema escondido en tu conciencia. Es, como decíamos, fundamental.
El teorema también\(\PageIndex{1}\) manejará cocientes de funciones continuas. Sin embargo, hay un pequeño detalle que hay que abordar primero. Obviamente, cuando consideramos la continuidad de\(f/g\) at\(a\), tenemos que asumir eso\(g(a) \neq 0\). Sin embargo,\(g\) puede ser cero en otros valores. ¿Cómo sabemos que cuando elegimos nuestra secuencia (\(x_n\)) convergiendo a una que no\(g(x_n)\) es cero? Esto estropear nuestra idea de usar el teorema correspondiente para las secuencias (Teorema 4.2.3 del Capítulo 4). Esto se puede manejar con el siguiente lema.
Si\(g\) is continuous at \(a\) and \(g(a) \neq 0\), entonces existe\(δ > 0\) tal que\(g(x) \neq 0\) para todos\(x ∈ (a - δ,a + δ)\).
Demostrar Lema\(\PageIndex{1}\).
- Pista
-
Considera el caso donde\(g(a) > 0\). Utilice la definición con\(ε = \frac{g(a)}{2}\). El cuadro está abajo; hazlo formal.
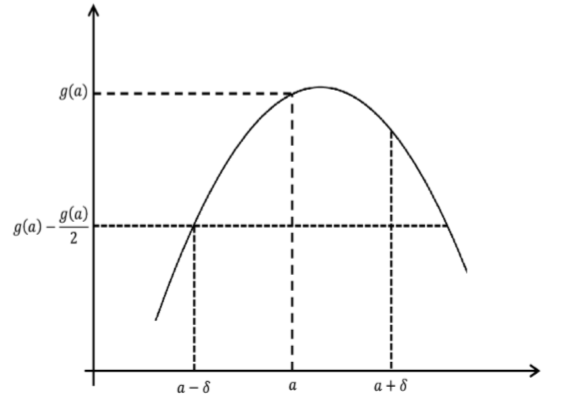
Figura\(\PageIndex{3}\): Cuadro para Lemma\(\PageIndex{1}\).
Para el caso\(g(a) < 0\), considere la función\(-g\).
Una consecuencia de este lema es que si empezamos con una secuencia (\(x_n\)) convergiendo a\(a\), entonces para\(n\) suficientemente grande,\(g(x_n) \neq 0\).
Utilice el teorema\(\PageIndex{1}\), para demostrar que si\(f\) y\(g\) son continuos en\(a\) y\(g(a) \neq 0\), entonces\(f/g\) es continuo en\(a\).
Supongamos que\(f\) es continuo en\(a\) y\(g\) es continuo en\(f(a)\). Entonces\(g \circ f\) es continuo en\(a\). [Obsérvese que\((g \circ f)(x) = g(f(x))\).]
Demostrar teorema\(\PageIndex{3}\).
- Utilizando la definición de continuidad.
- Usando el Teorema\(\PageIndex{1}\).
Los teoremas anteriores nos permiten construir funciones continuas a partir de otras funciones continuas. Por ejemplo, sabiendo eso\(f(x) = x\) y\(g(x) = c\) son continuos, podemos concluir que cualquier polinomio,
\[p(x) = a_nx^n + a_{n-1}x^{n-1} +\cdots + a_1x + a_0\]
también es continuo. También sabemos que funciones como\(f(x) = \sin (e^x)\) son continuas sin tener que depender de la definición.
Demostrar que cada una de las siguientes es una función continua en cada punto de su dominio.
- Cualquier polinomio.
- Cualquier función racional. (Una función racional se define como una relación de polinomios.)
- \(\cos x\)
- Las otras funciones trigonométricas:\(\tan (x), \cot (x), \sec (x), \csc (x)\)
¿Qué nos permite concluir que\(f(x) = sin(e^x)\) es continuo en cualquier momento a sin volver a referirnos a la definición de continuidad?
El teorema también\(\PageIndex{1}\) puede ser utilizado para estudiar la convergencia de secuencias. Por ejemplo, ya que\(f(x) = e^x\) es continuo en cualquier punto y\(\lim_{n \to \infty }\frac{n+1}{n} =1\), entonces\(\lim_{n \to \infty }e^{\left (\frac{n+1}{n} \right )} = e\). Esto también ilustra una cierta forma de pensar sobre las funciones continuas. Ellos son aquellos en los que podemos “conmutar” la función y un límite de una secuencia. Específicamente, si\(f\) es continuo en\(a\) y\(\lim_{n \to \infty }f(x_n) = f(a) = f(\lim_{n \to \infty }x_n)\).
Compute los siguientes límites. Asegúrese de señalar cómo está involucrada la continuidad.
- \(\lim_{n \to \infty }\sin \left ( \frac{n\pi }{2n+1} \right )\)
- \(\lim_{n \to \infty }\sqrt{\frac{n}{n^2+1}}\)
- \(\lim_{n \to \infty }e^{\left (\sin (\frac{1}{n}) \right )}\)
Tener esta formulación rigurosa de continuidad es necesaria para probar el Teorema del Valor Extremo y el Teorema del Valor Medio. Sin embargo, hay una pieza más del rompecabezas que abordar antes de que podamos probar estos teoremas.
Esto lo haremos en el siguiente capítulo, pero antes de continuar es el momento de definir un concepto fundamental que probablemente fue uno de los primeros que aprendiste en el cálculo: los límites.