11.10: Resolviendo el problema de Dirichlet para funciones armónicas
- Page ID
- 109895
En general, un problema de Dirichlet en una región\(A\) le pide resolver una ecuación diferencial parcial en\(A\) donde se\(A\) especifican los valores de la solución en el límite de.
Encuentra una función\(u\) armónica en el disco de la unidad de tal manera que
\[u(e^{i \theta}) = \begin{cases} 1 & \text{ for } 0 < \theta < \pi \\ 0 & \text{ for } -\pi < \theta < 0 \end{cases}\]
Este es un problema de Dirichlet porque se especifican los valores de\(u\) on the boundary. La ecuación diferencial parcial está implícita al requerir que\(u\) sea armónica, es decir, requerimos\(\nabla ^2 u = 0\). Vamos a resolver este problema en su momento.
Funciones armónicas en el medio plano superior
Nuestra estrategia será resolver el problema de Dirichlet para funciones armónicas en el medio plano superior y luego transferir estas soluciones a otros dominios.
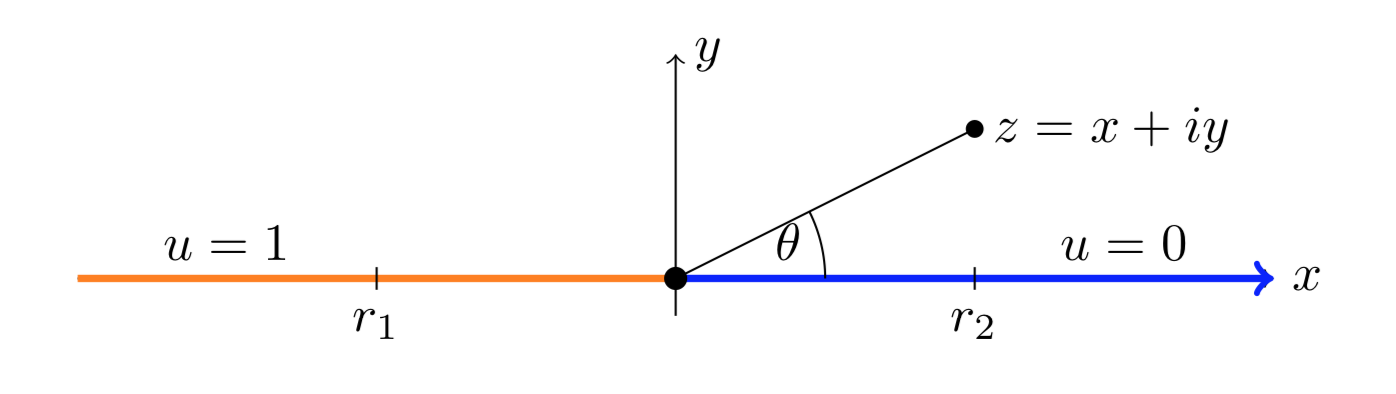
Encontrar una función armónica\(u(x, y)\) en el medio plano superior que satisfaga la condición de límite
\[u(x, 0) = \begin{cases} 1 & \text{ for } x < 0 \\ 0 & \text{ for } x > 0 \end{cases}\]
Solución
Podemos escribir una solución explícitamente como
\[u(x, y) = \dfrac{1}{\pi} \theta,\]
donde\(\theta\) esta el argumento de\(z = x + iy\). Ya que sólo estamos trabajando en el medio plano superior podemos tomar cualquier rama conveniente con corte de rama en el medio plano inferior, digamos\(-\pi /2 < \theta < 3 \pi /2\).
Para mostrar\(u\) es realmente una solución, tenemos que verificar dos cosas:
- \(u\)satisface las condiciones de contorno
- \(u\)es armónico.
Ambos son sencillos. Primero, mira el punto\(r_2\) en el\(x\) eje positivo. Esto tiene argumento\(\theta = 0\), entonces\(u(r_2, 0) = 0\). De igual manera\(\text{arg} (r_1) = \pi\), así\(u(r_1, 0) = 1\). Así, hemos mostrado el punto (1).
Para ver punto (2) recuerda que
\[\log (z) = \log (r) + i \theta.\]
Entonces,
\[u = \text{Re} (\dfrac{1}{\pi i} \log (z)).\]
Ya que es la parte real de una función analítica,\(u\) es armónica.
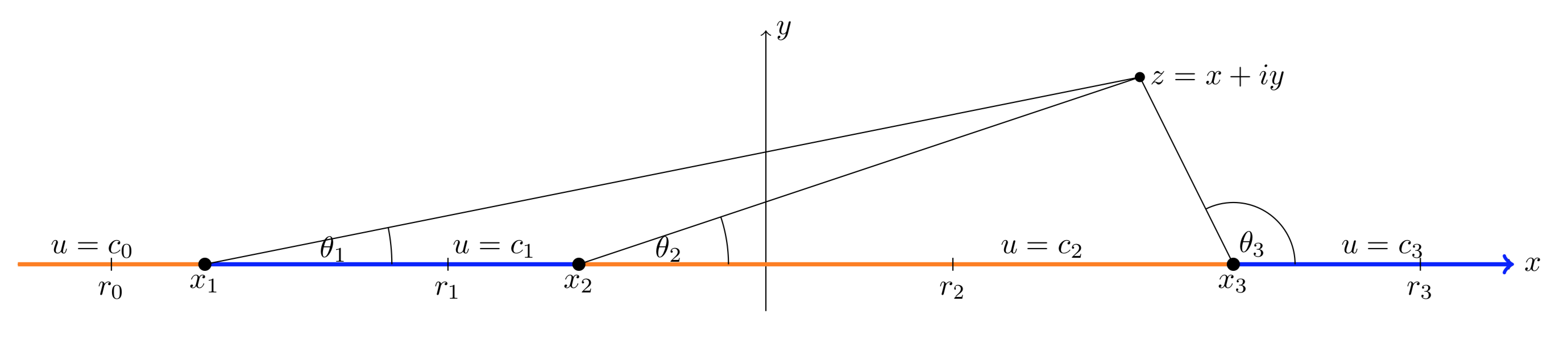
Supongamos\(x_1 < x_2 < x_3\). Encontrar una función armónica\(u\) en el medio plano superior que satisfaga la condición de límite
\[u(x, 0) = \begin{cases} c_0 & \text{ for } x < x_1 \\ c_1 & \text{ for } x_1 < x < x_2 \\ c_2 & \text{ for } x_2 < x < x_3 \\ c_3 & \text{ for } x_3 < x \end{cases}\]
Solución
Imitamos el ejemplo anterior y escribimos la solución
\[u(x, y) = c_3 + (c_2 - c_3) \dfrac{\theta_3}{\pi} + (c_1 - c_2) \dfrac{\theta_2}{\pi} + (c_0 - c_1) \dfrac{\theta_1}{\pi}.\]
Aquí, los\(\theta_j\) son los ángulos que se muestran en la figura. Una vez más, elegimos una rama de la\(\theta\) que tiene\(0 < \theta < \pi\) para puntos en el medio plano superior. (Por ejemplo la sucursal\(-\pi /2 < \theta < 3\pi /2\).)
Para convencerte de que\(u\) satisface la condición límite prueba algunos puntos:
- En\(r_3\): todos los\(\theta_j = 0\). Entonces,\(u(r_3, 0) = c_3\) según se requiera.
- En\(r_2\):\(\theta_1 = \theta_2 = 0\),\(\theta_3 = \pi\). Entonces,\(u(r_2, 0) = c_3 + c_2 - c_3 = c_2\) según se requiera.
- Asimismo, at\(r_1\) y\(r_0\),\(u\) tienen los valores correctos.
Como antes,\(u\) es armónico porque es la parte real de la función analítica
\[\Phi (z) = c_3 + \dfrac{(c_2 - c_3)}{\pi i} \log (z - x_3) + \dfrac{(c_1 - c_2)}{\pi i} \log (z - x_2) + \dfrac{(c_1 - c_0)}{\pi i} \log (z - x_1).\]
Funciones armónicas en el disco de la unidad
Intentemos resolver un problema similar al del Ejemplo 11.9.1..
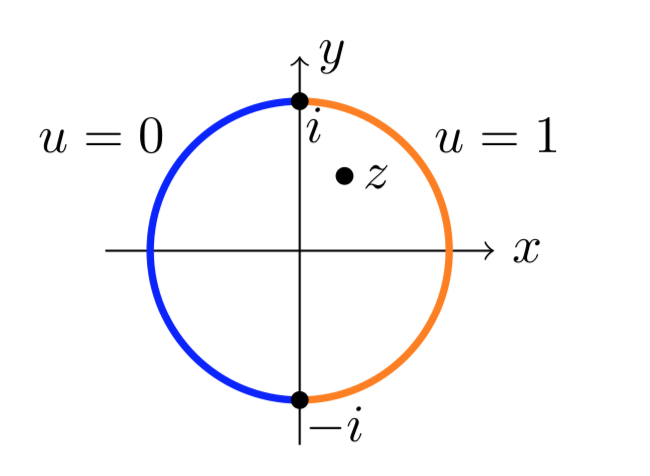
Encuentra una función\(u\) armónica en el disco de la unidad de tal manera que
\[u (e^{i \theta}) = \begin{cases} 1 & \text{ for } -\pi /2 < \theta < \pi /2 \\ 0 & \text{ for } \pi /2 < \theta < 3\pi /2 \end{cases}\]
Solución
Nuestra estrategia es comenzar con un mapa conforme\(T\) desde el medio plano superior hasta el disco unitario. Podemos usar este mapa para llevar el problema de nuevo al medio plano superior. Lo resolvemos ahí y luego empujamos la solución de nuevo al disco.
Llamemos al disco\(D\), al medio plano superior\(H\). Dejar\(z\) ser la variable on\(D\) y\(w\) la variable on\(H\). De vuelta en el Ejemplo 11.7.4 encontramos un mapa de\(H\) a\(D\). El mapa y su inverso son
\[z = T(w) = \dfrac{w - i}{w + i}, \ \ \ \ \ \ \ \ w = T^{-1} (z) = \dfrac{iz + i}{-z + 1}.\]
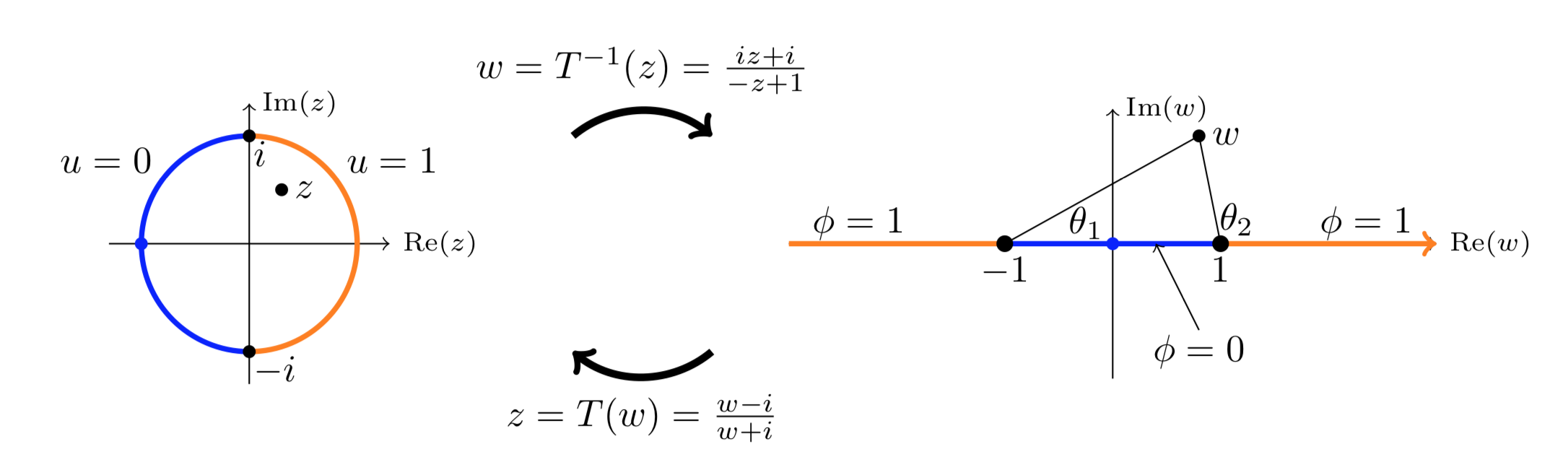
La función\(u\) on\(D\) es transformada por\(T\) a una función\(\phi\) on\(H\). Las relaciones son
\[u(z) = \phi \circ T^{-1} (z)\ \ \ \ \ \ \ \ \text{or} \ \ \ \ \ \ \ \ \phi (w) = u \circ T(w)\]
Estas relaciones determinan los valores límite\(\phi\) de aquellos para los que nos dieron\(u\). Calculamos:
\(T^{-1} (i) = -1\),\(T^{-1} (-i) = 1\),\(T^{-1} (1) = \infty\),\(T^{-1} (-1) = 0\).
Esto muestra que el límite del semicírculo izquierdo\(D\) se mapeó al segmento [-1, 1] en el eje real. Asimismo, el semicírculo derecho mapea a las dos medias líneas mostradas. (Literalmente, al 'segmento' 1\(\infty\) a -1.)
Sabemos resolver el problema de una función armónica\(\phi\) en\(H\):
\[\phi (w) = 1 - \dfrac{1}{\pi} \theta _2 + \dfrac{1}{\pi} \theta _1 = \text{Re} (1 - \dfrac{1}{\pi i} \log (w - 1) + \dfrac{1}{\pi i} \log (w + 1)).\]
Transformando esto de nuevo al disco que tenemos
\[u(z) = \phi \circ T^{-1} (z) = \text{Re} (1 - \dfrac{1}{\pi i} \log (T^{-1} (z) - 1) + \dfrac{1}{\pi i} \log (T^{-1} (z) + 1)).\]
Si quisiéramos, podríamos simplificar esto un poco usando la fórmula para\(T^{-1}\).


