12.2: Criterio Nyquist para la estabilidad
- Page ID
- 109823
El criterio Nyquist es una técnica gráfica para indicar si un sistema lineal inestable invariable en el tiempo puede estabilizarse usando un bucle de retroalimentación negativa. Analizaremos un poco más de cerca dichos sistemas cuando estudiemos la transformación de Laplace en el siguiente tema. Para este tema nos contentaremos con una declaración del problema con sólo el más mínimo contexto físico.
Ya ha encontrado sistemas lineales invariantes de tiempo en 18.03 (o su equivalente) cuando resolvió ecuaciones diferenciales lineales de coeficiente constante.
Funciones del sistema
Un sistema lineal invariante de tiempo tiene una función de sistema que es una función de una variable compleja. Por lo general, la variable compleja se denota por\(s\) y se usa una letra mayúscula para la función del sistema.
Dejar\(G(s)\) ser tal función del sistema. Haremos una suposición estándar que\(G(s)\) es meromórfica con un número finito de polos (finitos). Esta suposición se sostiene en muchos casos interesantes. Por ejemplo, muy a menudo\(G(s)\) es una función racional\(Q(s)/P(s)\) (\(Q\)y\(P\) son polinomios).
Nos preocuparemos por la estabilidad del sistema.
El sistema con función de sistema\(G(s)\) se llama estable si todos los polos de\(G\) están en el semiplano izquierdo. Es decir, si todos los polos de\(G\) tienen parte real negativa.
El sistema se llama inestable si alguno de los polos está en el medio plano derecho, es decir, tiene parte real positiva.
Para el caso de borde donde ningún polo tiene parte real positiva, pero algunos son puros imaginarios llamaremos al sistema marginalmente estable. Este caso se puede analizar utilizando nuestras técnicas. Para nuestros propósitos requeriría y un contorno sangría a lo largo del eje imaginario. Si tenemos tiempo haremos el análisis.
¿El sistema con función de sistema es\(G(s) = \dfrac{s}{(s + 2) (s^2 + 4s + 5)}\) estable?
Solución
Los polos son\(-2, -2\pm i\). Al estar todos en el medio plano izquierdo, el sistema es estable.
¿El sistema con función de sistema es\(G(s) = \dfrac{s}{(s^2 - 4) (s^2 + 4s + 5)}\) estable?
Solución
Los polos son\(\pm 2, -2 \pm i\). Dado que un polo está en el medio plano derecho, el sistema es inestable.
¿El sistema con función de sistema es\(G(s) = \dfrac{s}{(s + 2) (s^2 + 4)}\) estable?
Solución
Los polos son\(-2, \pm 2i\). No hay postes en el medio plano derecho. Dado que hay polos en el eje imaginario, el sistema es marginalmente estable.
Terminología. Hasta el momento, hemos tenido cuidado de decir 'el sistema con función de\(G(s)\) sistema'. A partir de ahora nos dejaremos ser un poco más casuales y decir 'el\(G(s)\) sistema'. ¡Está perfectamente claro y rueda de la lengua un poco más fácil!
Diagramas de polo cero
Podemos visualizar\(G(s)\) usando un diagrama polo-cero. Este es un diagrama en el\(s\) plano -donde ponemos una pequeña cruz en cada polo y un pequeño círculo en cada cero.
Dar diagramas de polo cero para cada uno de los sistemas
\[G_1(s) = \dfrac{s}{(s + 2) (s^2 + 4s + 5)}, \ \ \ G_1(s) = \dfrac{s}{(s^2 - 4) (s^2 + 4s + 5)}, \ \ \ G_1(s) = \dfrac{s}{(s + 2) (s^2 + 4)}\]
Solución
Estos son los mismos sistemas que en los ejemplos que se acaban de arriba. Primero notamos que todos tienen un solo cero en el origen. Entonces ponemos un círculo en el origen y una cruz en cada polo.
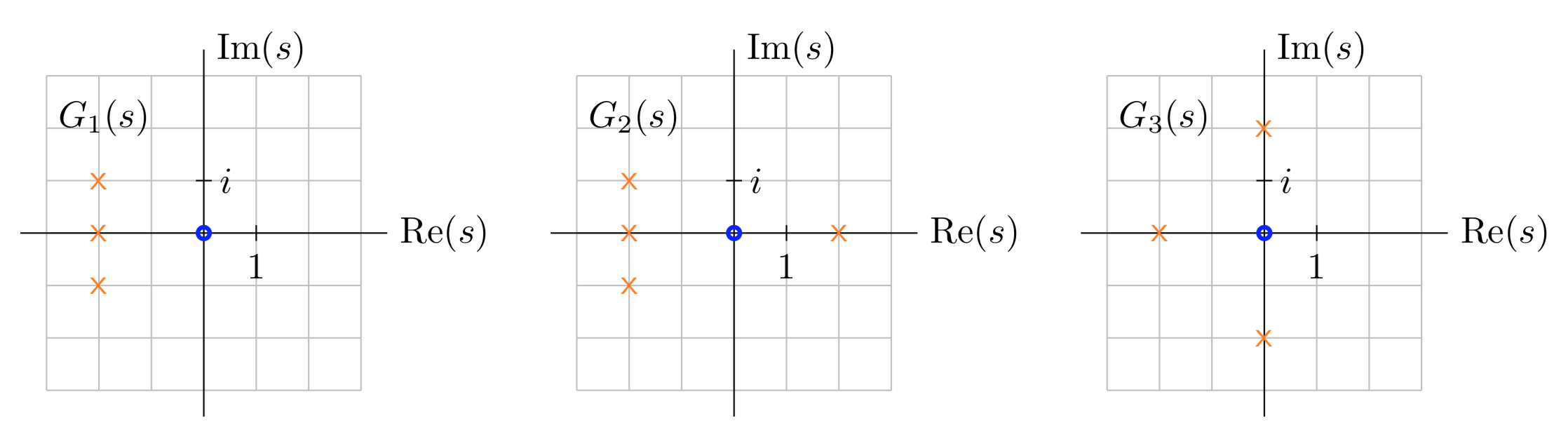
Diagramas de polo cero para los tres sistemas.
poco sobre la estabilidad
Esto es sólo para darte un poco de orientación física. Dada nuestra definición de estabilidad anterior, podríamos, en principio, discutir la estabilidad sin la menor idea de lo que significa para los sistemas físicos.
Los polos de\(G(s)\) corresponden a lo que se llaman modos del sistema. Un simple polo en\(s_1\) corresponde a un modo\(y_1 (t) = e^{s_1 t}\). El sistema es estable si todos los modos decaen a 0, es decir, si los polos están todos en el semiplano izquierdo.
Físicamente los modos nos dicen el comportamiento del sistema cuando la señal de entrada es 0, pero hay condiciones iniciales. Un polo con parte real positiva correspondería a un modo que va al infinito a medida que\(t\) crece. Ciertamente es razonable llamar inestable a un sistema que hace esto en respuesta a una señal cero (a menudo llamada 'sin entrada').
Para conectar esto a 18.03: si el sistema es modelado por una ecuación diferencial, los modos corresponden a las soluciones homogéneas\(y(t) = e^{st}\), donde\(s\) es una raíz de la ecuación característica. En 18.03 llamamos al sistema estable si cada solución homogénea decayó a 0. Es decir, si el sistema no forzado siempre se asentó en equilibrio.
Sistemas de bucle cerrado
Si el sistema con función del sistema\(G(s)\) es inestable, a veces puede estabilizarse mediante lo que se llama un bucle de retroalimentación negativa. El nuevo sistema se llama sistema de bucle cerrado. Su función de sistema viene dada por la fórmula de Black
\[G_{CL} (s) = \dfrac{G(s)}{1 + kG(s)},\]
donde\(k\) se llama el factor de retroalimentación. Simplemente aceptaremos esta fórmula. Cualquier clase o libro sobre teoría de control lo derivará por ti.
En este contexto\(G(s)\) se llama la función del sistema de bucle abierto.
Ya que\(G_{CL}\) es una función del sistema, podemos preguntar si el sistema es estable.
Los polos de la función del sistema de bucle cerrado\(G_{CL} (s)\) dada en la Ecuación 12.3.2 son los ceros de\(1 + kG(s)\).
- Prueba
-
Mirando la Ecuación 12.3.2, hay dos posibles fuentes de polos para\(G_{CL}\).
- Los ceros del denominador\(1 + k G\). El teorema los reconoce.
- Los polos de\(G\). Ya que\(G\) está tanto en el numerador como en el denominador del\(G_{CL}\) mismo debe quedar claro que los polos cancelan. Podemos mostrar esto formalmente usando la serie Laurent. Si\(G\) tiene un polo de orden\(n\) en\(s_0\) entonces
\[G(s) = \dfrac{1}{(s - s_0)^n} (b_n + b_{n - 1} (s - s_0) + \ ... a_0 (s - s_0)^n + a_1 (s - s_0)^{n + 1} + \ ...),\]
donde\(b_n \ne 0\). Entonces,
\[\begin{array} {rcl} {G_{CL} (s)} & = & {\dfrac{\dfrac{1}{(s - s_0)^n} (b_n + b_{n - 1} (s - s_0) + \ ... a_0 (s - s_0)^n + \ ...)}{1 + \dfrac{k}{(s - s_0)^n} (b_n + b_{n - 1} (s - s_0) + \ ... a_0 (s - s_0)^n + \ ...)}} \\ { } & = & {\dfrac{(b_n + b_{n - 1} (s - s_0) + \ ... a_0 (s - s_0)^n + \ ...)}{(s - s_0)^n + k (b_n + b_{n - 1} (s - s_0) + \ ... a_0 (s - s_0)^n + \ ...)}} \end{array}\]
que es claramente analítico en\(s_0\). (En\(s_0\) es igual\(b_n/(kb_n) = 1/k\).)
Establezca el factor de retroalimentación\(k = 1\). Supongamos que\(a\) es real, ¿para qué valores de\(a\) es\(G(s) = \dfrac{1}{s + a}\) estable el sistema de bucle abierto? ¿Para qué valores de\(a\) es\(G_{CL} (s)\) estable el sistema de bucle cerrado correspondiente?
(No hay ninguna razón particular que\(a\) necesite ser real en este ejemplo. Pero en los sistemas físicos, los polos complejos tenderán a venir en pares conjugados).
Solución
\(G(s)\)tiene un polo en\(s = -a\). Por lo tanto, es estable cuando el polo está en el medio plano izquierdo, es decir, para\(a > 0\).
La función del sistema de bucle cerrado es
\[G_{CL} (s) = \dfrac{1/(s + a)}{1 + 1/(s + a)} = \dfrac{1}{s + a + 1}.\]
Esto tiene un polo en\(s = -a - 1\), por lo que es estable si\(a > -1\). El bucle de retroalimentación ha estabilizado los sistemas de bucle abierto inestables con\(-1 < a \le 0\). (En realidad, para\(a = 0\) el bucle abierto es marginalmente estable, pero está completamente estabilizado por el bucle cerrado.)
El álgebra que implica cancelar el\(s + a\) término en los denominadores es exactamente la cancelación que hace que los polos de singularidades\(G\) removibles en\(G_{CL}\).
Supongamos\(G(s) = \dfrac{s + 1}{s - 1}\). ¿El sistema de bucle abierto es estable? ¿El sistema de bucle cerrado es estable cuando\(k = 2\).
Solución
\(G(s)\)tiene un poste en el medio plano derecho, por lo que el sistema de bucle abierto no es estable. La función del sistema de bucle cerrado es
\[G_{CL} (s) = \dfrac{G}{1 + kG} = \dfrac{(s + 1)/(s - 1)}{1 + 2(s + 1)/(s - 1)} = \dfrac{s + 1}{3s + 1}.\]
El único polo está en\(s = -1/3\), por lo que el sistema de bucle cerrado es estable. Este es un caso donde la retroalimentación estabilizó un sistema inestable.
\(G(s) = \dfrac{s - 1}{s + 1}\). ¿El sistema de bucle abierto es estable? ¿El sistema de bucle cerrado es estable cuando\(k = 2\).
Solución
La única gráfica de\(G(s)\) está en el medio plano izquierdo, por lo que el sistema de bucle abierto es estable. La función del sistema de bucle cerrado es
\[G_{CL} (s) = \dfrac{G}{1 + kG} = \dfrac{(s - 1)/(s + 1)}{1 + 2(s - 1)/(s + 1)} = \dfrac{s - 1}{3s - 1}.\]
Este tiene un polo en\(s = 1/3\), por lo que el sistema de bucle cerrado es inestable. Este es un caso donde la retroalimentación desestabilizó un sistema estable. ¡Puede suceder!
Parcelas Nyquist
Para la gráfica y criterio Nyquist la curva siempre\(\gamma\) será el\(s\) eje imaginario. Eso es
\[s = \gamma (\omega) = i \omega, \text{ where } -\infty < \omega < \infty.\]
Para un sistema\(G(s)\) y un factor de retroalimentación\(k\), la gráfica de Nyquist es la gráfica de la curva
\[w = k G \circ \gamma (\omega) = kG(i \omega).\]
Es decir, la trama Nyquist es la imagen del eje imaginario debajo del mapa\(w = kG(s)\).
En\(\gamma (\omega)\) la variable es un omega griego y en\(w = G \circ \gamma\) tenemos un doble-u.
Vamos\(G(s) = \dfrac{1}{s + 1}\). Dibuja la trama Nyquist con\(k = 1\).
Solución
En el caso\(G(s)\) es una transformación lineal fraccionaria, por lo que sabemos que mapea el eje imaginario a un círculo. Es fácil comprobar que es el círculo por el origen con centro\(w = 1/2\). También se puede comprobar que se recorre en el sentido de las agujas del reloj.
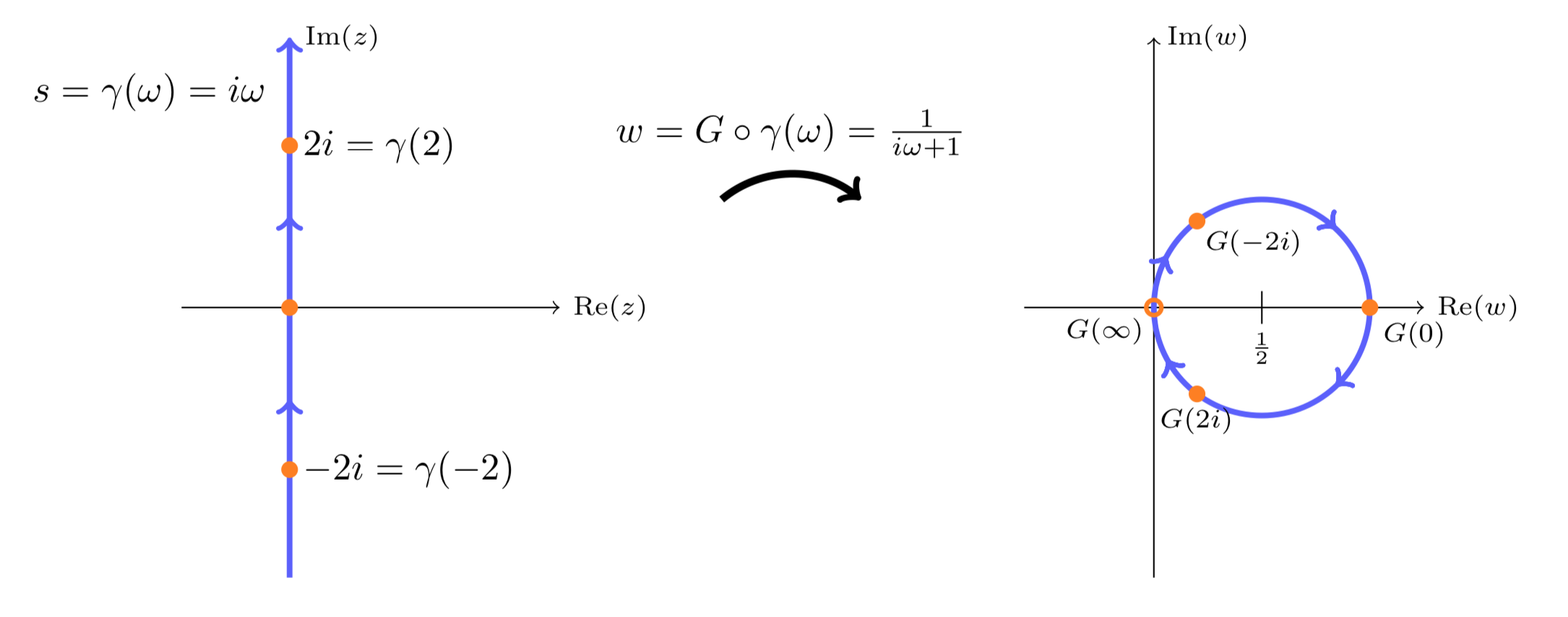
Parcela nyquist de\(G(s) = 1/(s + 1)\), con\(k = 1\).
Tomemos\(G(s)\) del ejemplo anterior. Describir la gráfica Nyquist con factor de ganancia\(k = 2\).
Solución
La trama Nyquist es la gráfica de\(kG(i \omega)\). El factor\(k = 2\) escalará el círculo en el ejemplo anterior por 2. Es decir, la trama Nyquist es el círculo por el origen con centro\(w = 1\).
En general, el factor de retroalimentación sólo escalará la trama Nyquist.
Criterio Nyquist
El criterio Nyquist da un método gráfico para verificar la estabilidad del sistema de bucle cerrado.
Supongamos que\(G(s)\) tiene un número finito de ceros y polos en el medio plano derecho. También supongamos que\(G(s)\) decae a 0 como\(s\) va al infinito. Entonces el sistema de bucle cerrado con factor de retroalimentación\(k\) es estable si y solo si el número de bobinado de la gráfica Nyquist alrededor\(w = -1\) es igual al número de polos de\(G(s)\) en el medio plano derecho.
Más brevemente,
\[G_{CL} (s) \text{ is stable } \Leftrightarrow \text{ Ind} (kG \circ \gamma, -1) = P_{G, RHP}\]
Aquí,\(\gamma\) es el\(s\) eje imaginario y\(P_{G, RHP}\) es el número o polos de la función original del sistema de bucle abierto\(G(s)\) en el medio plano derecho.
- Prueba
-
\(G_{CL}\)es estable exactamente cuando todos sus polos están en el semiplano izquierdo. Ahora bien, recordemos que los polos de\(G_{CL}\) son exactamente los ceros de\(1 + k G\). Entonces, la estabilidad de\(G_{CL}\) es exactamente la condición de que el número de ceros\(1 + kG\) en el medio plano derecho sea 0.
Trabajemos con un contorno familiar.
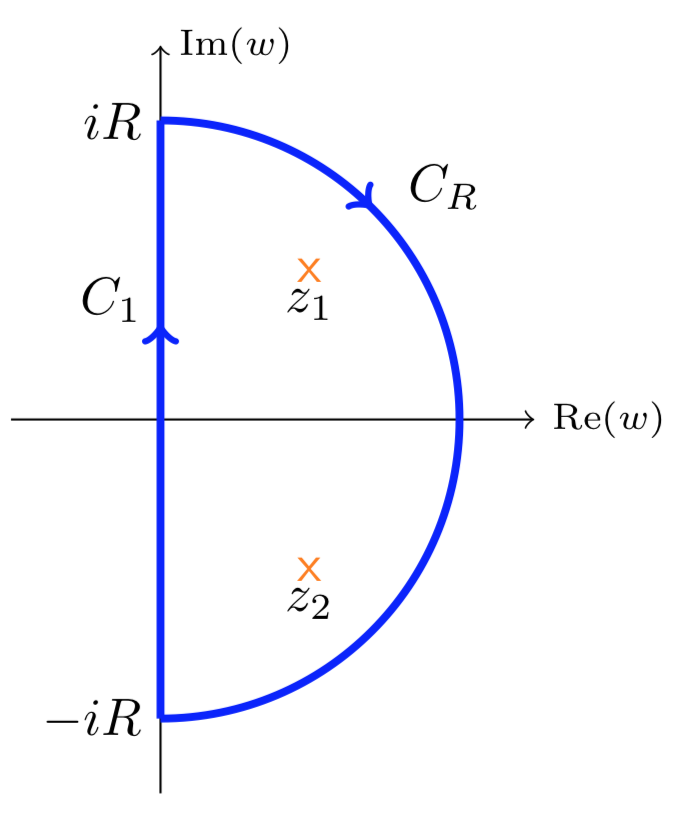
Vamos\(\gamma_R = C_1 + C_R\). Tenga en cuenta que\(\gamma_R\) se recorre en la\(clockwise\) dirección. Elija lo suficientemente\(R\) grande como para que el (número finito) de polos y ceros de\(G\) en el medio plano derecho estén todos dentro\(\gamma_R\). Ahora podemos aplicar la Ecuación 12.2.4 en el corolario al principio argumental para\(kG(s)\) y\(\gamma\) para obtener
\[-\text{Ind} (kG \circ \gamma_R, -1) = Z_{1 + kG, \gamma_R} - P_{G, \gamma_R}\]
(El signo menos se debe a la dirección de las agujas del reloj de la curva). Por lo tanto, para todos los grandes\(R\)
\[\text{the system is stable } \Leftrightarrow \ Z_{1 + kG, \gamma_R} = 0 \ \Leftrightarow \ \text{ Ind} (kG \circ \gamma_R, -1) = P_{G, \gamma_R}\]
Por último, podemos dejar\(R\) ir al infinito. La suposición de que\(G(s)\) decae 0 a como\(s\) va a\(\infty\) implica que en el límite, toda la curva\(kG \circ C_R\) se convierte en un solo punto en el origen. Entonces en el límite\(kG \circ \gamma_R\) se convierte\(kG \circ \gamma\). \(\text{QED}\)
Ejemplos usando el mathlet Nyquist Plot
El criterio Nyquist es un método visual que requiere alguna forma de producir la gráfica Nyquist. Para ello utilizaremos uno de los Mathlets del MIT (ligeramente modificado para nuestros fines). Abra el applet Nyquist Plot en
http://web.mit.edu/jorloff/www/jmoapplets/nyquist/nyquistCrit.html
Juega con el applet, lee la ayuda.
Ahora actualice el navegador para restaurar el applet a su estado original. Marque la\(Formula\) casilla. La fórmula es una manera fácil de leer los valores de los polos y ceros de\(G(s)\). En su estado original, el applet debe tener un cero en\(s = 1\) y polos en\(s = 0.33 \pm 1.75 i\).
El gráfico de la izquierda es el diagrama polo-cero. La gráfica de la derecha es la gráfica Nyquist.
Para tener una idea de la trama Nyquist. Mira el diagrama de polos y usa el ratón para arrastrar el punto amarillo hacia arriba y hacia abajo del eje imaginario. Su imagen debajo\(kG(s)\) trazará la trama nyquis.
Observe que cuando el punto amarillo está en cualquiera de los extremos del eje su imagen en la gráfica Nyquist está cerca de 0.
Refresca la página, para volver a poner el cero y los polos a su estado original. Hay dos polos en el medio plano derecho, por lo que el sistema de bucle abierto\(G(s)\) es inestable. Con\(k =1\), ¿cuál es el número sinuoso de la trama Nyquist alrededor del -1? ¿El sistema de bucle cerrado es estable?
Solución
La curva se enrolla dos veces alrededor de -1 en sentido antihorario, por lo que el número sinuoso\(\text{Ind} (kG \circ \gamma, -1) = 2\). Dado que el número de polos de\(G\) en el medio plano derecho es el mismo que este número de bobinado, el sistema de bucle cerrado es estable.
Con los mismos polos y ceros, mueva el\(k\) control deslizante y determine qué rango de\(k\) hace estable el sistema de bucle cerrado.
Solución
Cuando\(k\) es pequeña la trama Nyquist tiene el número sinuoso 0 alrededor de -1. Para estos valores de\(k\),\(G_{CL}\) es inestable. A medida que\(k\) aumenta, en algún lugar entre\(k = 0.65\) y\(k = 0.7\) el número de bobinado salta de 0 a 2 y el sistema de bucle cerrado se vuelve estable. Esto continúa hasta que\(k\) esté entre 3. 10 y 3. 20, momento en el que el número de bobinado se convierte en 1 y\(G_{CL}\) se vuelve inestable.
Respuesta: El sistema de bucle cerrado es estable para\(k\) (aproximadamente) entre 0. 7 y 3. 10.
En el problema anterior ¿podrías determinar analíticamente el rango de\(k\) donde\(G_{CL} (s)\) es estable?
Solución
¡Sí! Esto es posible para sistemas pequeños. Es más desafiante para los sistemas de orden superior, pero hay métodos que no requieren computar los polos. En este caso, tenemos
\[G_{CL} (s) = \dfrac{G(s)}{1 + kG(s)} = \dfrac{\dfrac{s - 1}{(s - 0.33)^2 + 1.75^2}}{1 + \dfrac{k(s - 1)}{(s - 0.33)^2 + 1.75^2}} = \dfrac{s - 1}{(s - 0.33)^2 + 1.75^2 + k(s - 1)} \nonumber\]
Entonces los polos son las raíces de
\[(s - 0.33)^2 + 1.75^2 + k(s - 1) = s^2 + (k - 0.66)s + 0.33^2 + 1.75^2 - k \nonumber\]
Para una cuadrática con coeficientes positivos las raíces ambas tienen parte real negativa. Esto sucede cuando
\[0.66 < k < 0.33^2 + 1.75^2 \approx 3.17. \nonumber\]
Qué pasa cuando\(k\) va a 0.
Solución
En\(k\) cuanto a 0, la trama Nyquist se reduce a un solo punto en el origen. En este caso el número de bobinado alrededor de -1 es 0 y el criterio Nyquist dice que el sistema de bucle cerrado es estable si y solo si el sistema de bucle abierto es estable.
Esto debería tener sentido, ya que con\(k = 0\),
\[G_{CL} = \dfrac{G}{1 + kG} = G. \nonumber\]
Hacer un sistema con los siguientes ceros y polos:
- Un par de ceros a\(0.6 \pm 0.75i\).
- Un par de postes en\(-0.5 \pm 2.5i\).
- Un solo polo a 0.25.
¿Cuándo es estable el sistema de bucle cerrado correspondiente\(k = 6\)?
Solución
La respuesta es no, no\(G_{CL}\) es estable. \(G\)tiene un polo en la mitad derecha del plano. El mathlet muestra los vientos de la trama Nyquist una vez alrededor\(w = -1\) en la\(clockwise\) dirección. Por lo que el número de bobinado es -1, que no equivale al número de polos de\(G\) en el medio plano derecho.
Si configuramos\(k = 3\), el sistema de bucle cerrado es estable.