18.7: Productos Binomiales Especiales
( \newcommand{\kernel}{\mathrm{null}\,}\)
Tres productos binomiales ocurren con tanta frecuencia en álgebra que los designamos como productos binomiales especiales. Los hemos visto antes, pero los volveremos a estudiar por su importancia como dispositivos ahorradores de tiempo y en la resolución de ecuaciones (que estudiaremos en un capítulo posterior).
Estos productos especiales se pueden mostrar como los cuadrados de un binomio
(a+b)2ya−b)2
y como la suma y diferencia de dos términos.
(a+b)(a−b)
Hay dos reglas simples que nos permiten expandir (multiplicar) fácilmente estos binomios. Bien vale la pena memorizarlos, ya que ahorrarán mucho tiempo en el futuro.
Ampliando(a+b)2 y(a−b)2
Para cuadrar un binomio:
1. Cuadrado el primer término.
2. Toma el producto de los dos términos y duplicalo.
3. Cuadrarse el último término.
4. Sumar los tres resultados juntos
(a+b)2=a2+2ab+b2
(a−b)2=a2−2ab+b2
Expansión (a+b) (a−b)
Para ampliar la suma y diferencia de dos términos: †
- Cuadrar el primer término y cuadrar el segundo término.
- Restar el cuadrado del segundo término del cuadrado del primer término.
(a+b)(a−b)=a2−b2
Conjunto de Muestras A
\ (
(x+4) ^ {2}
\)
Cuadrar el primer término:x2.
El producto de ambos términos es4x. Doblarlo:8x.
Cuadrar el último término: 16.
Agréguelos juntos:x2+8x+16
(x+4)2=x2+8x+16
Tenga en cuenta que(x+4)2≠x2+42. ¡Falta el8x término!
\ (
(a-8) ^ {2}
\)
Cuadrar el primer término:a2.
El producto de ambos términos es−8a. Doblarlo:−16a.
Cuadrar el último término: 64.
Sumarlos juntos:a2+(−16a)+64
(a−8)2=a2−16a+64
Observe que el signo del último término en esta expresión es “+.” Esto siempre sucederá ya que el último término resulta de que un número está al cuadrado. Cualquier número distinto de cero veces en sí mismo siempre es positivo.
(+)(+)=+y(−)(−)=+
El signo del segundo término en el trinomio siempre será el signo que ocurra dentro de los paréntesis.
\ (
(y-1) ^ {2}
\)
Cuadrar el primer término:y2.
El producto de ambos términos es−y. Doblarlo:−2y.
Cuadrar el último término: +1.
Agréguelos juntos:y2+(−2y)+1
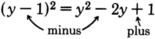
\ (
(5x+3) ^ {2}
\)
Cuadrar el primer término:25x2.
El producto de ambos términos es15x. Doblarlo:30x.
Cuadrar el último término: 9.
Agréguelos juntos:25x2+30x+9
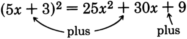
\ (
(7b-2) ^ {2}
\)
Cuadrar el primer término:49b2.
El producto de ambos términos es−14b. Doblarlo:−28b.
Cuadrar el último término: 4.
Agréguelos juntos:49b2+(−28b)+4
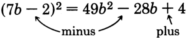
\ (
(x+6) (x-6)
\)
Cuadrar el primer término:x2.
Restar el cuadrado del segundo término (36) del cuadrado del primer término:x2−36
(x+6)(x−6)=x2−36
\ (
(4a−12) (4a+12)
\)
Cuadrar el primer término:16a2.
Restar el cuadrado del segundo término (144) del cuadrado del primer término:16a2−144
(4a−12)(4a+12)=16a2−144
\ (
(6x+8y) (6x−8y)
\)
Cuadrar el primer término:36x2.
Restar el cuadrado del segundo término (64y2) del cuadrado del primer término:36x2−64y2
(6x+8y)(6x−8y)=36x2−64y2
Conjunto de práctica A
Encuentra los siguientes productos.
(x+5)2
- Contestar
-
x2+10x+25
(x+7)2
- Contestar
-
x2+14x+49
(y−6)2
- Contestar
-
y2−12y+36
(3a+b)2
- Contestar
-
9a2+6ab+b2
(9m−n)2
- Contestar
-
81m2−18mn+n2
(10x−2y)2
- Contestar
-
100x2−40xy+4y2
(12a−7b)2
- Contestar
-
144a2−168ab+49b2
(5h−15k)2
- Contestar
-
25h2−150hk+225k2
Ejercicios
Para los siguientes problemas, encuentra los productos.
(x+3)2
- Contestar
-
x2+6x+9
(x+5)2
(x+8)2
- Contestar
-
x2+16x+64
(x+6)2
(y+9)2
- Contestar
-
y2+18y+81
(y+1)2
(a−4)2
- Contestar
-
a2−8a+16
(a−6)2
(a−7)2
- Contestar
-
a2−14a+49
(b+10)2
(b+15)2
- Contestar
-
b2+30b+225
(a−10)2
(x−12)2
- Contestar
-
x2−24x+144
(x+20)2
(y−20)2
- Contestar
-
y2−40y+400
(3x+5)2
(4x+2)2
- Contestar
-
16x2+16x+4
(6x−2)2
(7x−2)2
- Contestar
-
49x2−28x+4
(5a−6)2
(3a−9)2
- Contestar
-
9a2−54a+81
(3w−2z)2
(5a−3b)2
- Contestar
-
25a2−30ab+9b2
(6t−7s)2
(2h−8k)2
- Contestar
-
4h2−32hk+64k2
(a+12)2
(a+13)2
- Contestar
-
a2+23a+19
(x+34)2
(x+25)2
- Contestar
-
x2+45x+425
(x−23)2
(y−56)2
- Contestar
-
y2−53y+2536
(y+23)2
(x+1.3)2
- Contestar
-
x2+2.6x+1.69
(x+5.2)2
(a+0.5)2
- Contestar
-
a2+a+0.25
(a+0.08)2
(x−3.1)2
- Contestar
-
x2−6.2x+9.61
(y−7.2)2
(b−0.04)2
- Contestar
-
b2−0.08b+0.0016
(f−1.006)2
(x+5)(x−5)
- Contestar
-
x2−25
(x+6)(x−6)
(x+1)(x−1)
- Contestar
-
x2−1
(t−1)(t+1)
(f+9)(f−9)
- Contestar
-
f2−81
(y−7)(y+7)
(2y+3)(2y−3)
- Contestar
-
4y2−9
(5x+6)(5x−6)
(2a−7b)(2a+7b)
- Contestar
-
4a2−49b2
(7x+3t)(7x−3t)
(5h−2k)(5h+2k)
- Contestar
-
25h2−4k2
(x+13)(x−13)
(a+29)(a−29)
- Contestar
-
a2−481
(x+73)(x−73)
(2b+67)(2b−67)
- Contestar
-
4b2−3649
(a+b)2Ampliar para demostrar que es igual aa2+2ab+b2.
(a−b)2Ampliar para demostrar que es igual aa2−2ab+b2.
- Contestar
-
(a−b)(a−b)=a2−ab−ab+b2=a2−2ab+b2
(a+b)(a−b)Ampliar para demostrar que es igual aa2−b2.
Rellena la etiqueta que falta en la siguiente ecuación.
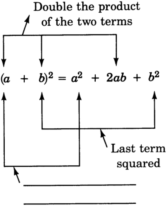
- Contestar
-
Primer trimestre al cuadrado
Etiquete las partes de la ecuación a continuación.

Etiquete las partes de la ecuación a continuación.
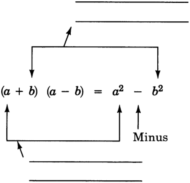
- Contestar
-
a) Cuadrarse el primer término.
b) Cuadrar el segundo término y restarlo del primer término.
Ejercicios para la revisión
Simplificar(x3y0z4)5.
Encuentra el valor de10−1⋅2−3
- Contestar
-
180
Encuentra el producto.
(x+6)(x−7).
Encuentra el producto.
(5m−3)(2m+3)
- Contestar
-
10m2+9m−9
Encuentra el producto.
(a+4)(a2−2a+3)


