4.1: Funciones de dos variables
- Page ID
- 110553
Introducción
La vida real rara vez es tan simple como una entrada/una salida. Muchas relaciones dependen de muchas variables. Ejemplos:
- Si pongo un depósito en una cuenta que devenga intereses y la dejo reposar, la cantidad que tengo al final de 3 años depende de\(P\) (cuánto es mi depósito inicial),\(r\) (la tasa de interés anual) y\(n\) (el número de compuestos por año).
- La resistencia del aire en un ala en un túnel de viento depende de la forma del ala, la velocidad del viento, la orientación del ala (cabeceo, guiñada y balanceo), además de una miríada de otras cosas que no puedo comenzar a describir.
- El monto de tu factura de televisión por cable depende de la estructura de tarifas básica que hayas elegido y de cuántas películas de pago por visión hayas pedido.
Dado que el mundo real es tan complicado, queremos extender nuestras ideas de cálculo a funciones de varias variables.
Funciones de dos variables
Si\( x_1, x_2, x_3, \dots, x_n \) son números reales, entonces\( (x_1, x_2, x_3, \dots, x_n) \) se llama una\(n\) -tupla. Se trata de una extensión de pares y triples ordenados. Una función de\(n\) variables es una función cuyo dominio es algún conjunto de\(n\) -tuplas y cuyo rango es algún conjunto de números reales.
Por gran parte de lo que hacemos aquí, todo va a funcionar igual ya sea que estuviéramos trabajando con 2, 3, o 47 variables. Debido a que estamos tratando de que las cosas sean un poco más simples, nos concentraremos en funciones de dos variables.
Una función de dos variables es una función, es decir, a cada entrada se asocia exactamente una salida.
Las entradas son pares ordenados,\((x, y)\). Las salidas son números reales (cada salida es un único número real). El dominio de una función es el conjunto de todas las entradas posibles (pares ordenados); el rango es el conjunto de todas las salidas posibles (números reales).
La función puede ser escrita\(z = f(x,y)\).
Las funciones de dos variables se pueden describir numéricamente (una tabla), gráfica, algebraicamente (una fórmula), o en inglés.
A menudo ahora llamaremos a lo familiar\(y = f(x)\) una función de una variable.
El costo de alquilar un auto depende de cuántos días lo guardes y qué tan lejos conduzcas. Representar esto usando una función.
Solución
\(d\)Sea el número de días que alquile el auto, y\(m\) sea el número de millas que conduce. Entonces el costo del alquiler de autos\(C(d, m)\) es una función de dos variables.
La demanda de bollos de hot dog depende del precio de los bollos de hot dog y también del precio de los hot dogs. Representar esto como una función.
Solución
La demanda\( q_B=f\left(p_B,p_D \right) \) es una función de dos variables. (La demanda de perritos calientes también depende del precio tanto de los perros como de los bollos).
Fórmulas y Tablas
Así como en el caso de las funciones de una variable, podemos mostrar una función de dos variables en una tabla. Las dos entradas se muestran en el margen (fila superior, columna izquierda), y las salidas se muestran en las celdas interiores.
Aquí hay una tabla que muestra el costo\(C(d, m)\) en dólares por rentar un auto por\(d\) días y conducirlo\(m\) millas:
| \( d \)(etiquetas en la columna izquierda),\( m \) (etiquetas en la fila superior) | 100 | 200 | 300 | 400 |
| 1 | 55 | 70 | 85 | 100 |
| 2 | 95 | 110 | 125 | 140 |
| 3 | 135 | 150 | 165 | 180 |
- ¿Cuál es el costo de rentar un auto por 3 días y conducirlo a 200 millas?
- ¿Qué es\(C(100, 4)\)? ¿Qué es\(C(4, 100)\)?
- Supongamos que rentamos el auto por tres días. ¿Es\(C\) una función creciente de millas?
Solución
- Según la tabla, rentar el auto por tres días (fila con\(d = 3\)) y manejarlo 200 millas (columna con\(m = 200\)) costará $150 (en cursiva en la tabla).
- Cuidado ahora — la entrada es un par ordenado, así que en\(C(100, 4)\), el 100 tiene que ser un valor de\(d\) y el 4 tiene que ser un valor de\(m\). \(C(100, 4)\)sería el costo de rentar un auto por 100 días y conducirlo a 4 millas. Ese costo no está en la tabla. (Y esa sería una forma bastante tonta de alquilar un auto). Por otro lado,\(C(4, 100)\) es el costo de rentar por 4 días y conducir 100 millas —dice la mesa que costaría 175 dólares.
- Si sabemos que\(d\) se fija en 3, estamos mirando\(C(3, m)\). Esto es ahora una función de una variable: justa\(m\). Podemos ver la tabla que muestra los valores de esta función centrando nuestra atención solo en la fila donde\(d = 3\):
\( d \)(etiqueta en la columna izquierda),\( m \) (etiquetas en la fila superior) 100 200 300 400 3 135 150 165 180 Ahora podemos ver que si alquilamos por 3 días, el costo parece ser una función creciente del número de millas que manejamos, lo que no debería ser sorprendente.
La idea de fijar una variable y ver lo que le sucede a la función como la otra varía surgirá una y otra vez.
Es difícil mostrar una función de más de dos variables en una tabla. Pero es conveniente trabajar con fórmulas para funciones de dos variables, o tantas variables como quieras.
El costo\(C(d,m)\) en dólares por rentar un auto por\(d\) días y manejarlo\(m\) millas viene dado por la fórmula\[ C(d,m)=40d+0.15m. \nonumber \]
- ¿Cuál es el costo de rentar un auto por 3 días y conducirlo a 200 millas?
- ¿Qué es\(C(100, 4)\)? ¿Qué es\(C(4, 100)\)?
- Supongamos que rentamos el auto por 3 días. ¿Es\(C\) una función creciente de millas?
Solución
- \( C(3,200)=40(3)+0.15(200)=\$150 \). Este es el mismo valor que obtuvimos de la mesa. La fórmula nos dará las mismas respuestas para cualquiera de los valores de la tabla.
- \(C(100, 4)\)tiene perfecto sentido para la fórmula (incluso si no tiene sentido para alquilar realmente un automóvil). Entonces ahora podemos obtener una respuesta. Para rentar el auto por 100 días y conducirlo por 4 millas debe costar $4000.60. \(C(4, 100) = \$175\), como antes.
- Si arreglamos\(d = 3\), entonces\(C(d, m)\) se vuelve\(C(3, m) = 40(3) + 0.15m = 120 + 0.15m\). Sí, esta es una función creciente de\(m\) — podemos decir porque es lineal y su pendiente lo es\(0.15 \gt 0\).
Verificación de la realidad: la fórmula que da el costo del auto de alquiler tiene sentido para todos los valores de\(d\) y\(m\). Pero no es así como funciona el costo real: no se puede alquilar el auto por un número negativo de días o conducir un número negativo de millas. (Es decir, hay restricciones de dominio). Además, la mayoría de los acuerdos de renta de autos no computan un cargo por fracciones de días; redondean al siguiente número entero de días.
Vamos\( f(x,y,z,w)=35x^2w-\frac{1}{z}+yz^2 \). Evaluar\( f(0,1,2,3) \).
Solución
Recuerda que esta es una 4-tupla ordenada; asegúrate de que los números se sustituyan en los lugares correctos:\[ f(0,1,2,3)=35(0)^2(3)-\frac{1}{2}+(1)(2)^2=3.5 \nonumber \]
Gráficas
La gráfica de una función de dos variables es una superficie en el espacio tridimensional. Empecemos por mirar el sistema de coordenadas rectangulares tridimensionales, cómo ubicar puntos en tres dimensiones y la distancia entre puntos en tres dimensiones.
En el sistema de coordenadas rectangulares bidimensionales tenemos dos ejes de coordenadas que se encuentran en ángulo recto en el origen, y se necesitan dos números, un par ordenado\((x, y)\), para especificar la ubicación de coordenadas rectangulares de un punto en el plano (dos dimensiones).
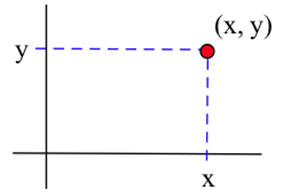
Cada par ordenado\((x, y)\) especifica la ubicación de exactamente un punto, y la ubicación de cada punto viene dada por exactamente un par ordenado\((x, y)\). \(y\)Los valores\(x\) y son las coordenadas del punto\((x, y)\).
La situación en tres dimensiones es muy similar. En el sistema de coordenadas rectangulares tridimensionales tenemos tres ejes de coordenadas que se encuentran en ángulo recto, y se necesitan tres números\((x, y, z)\), un triple ordenado, para especificar la ubicación de un punto.
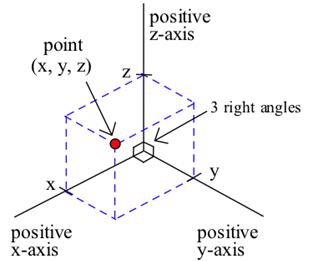
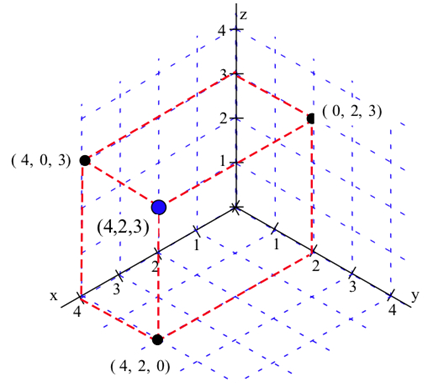
Cada triple ordenado\((x, y, z)\) especifica la ubicación de exactamente un punto, y la ubicación de cada punto viene dada por exactamente un triple ordenado\((x, y, z)\). Los\(z\) valores\(x\)\(y\),, y son las coordenadas del punto\((x, y, z)\). En la siguiente figura se muestra la ubicación del punto (4, 2, 3).
Normalmente usamos una orientación a la derecha. Para ver lo que esto significa, imagina tu mano derecha delante de ti con la palma hacia tu cara, tu pulgar apuntando hacia arriba, tu dedo índice hacia afuera, y tu siguiente dedo hacia tu cara (y los dos dedos inferiores doblados hacia la palma). Luego, en el sistema de coordenadas de la derecha, tu pulgar apunta a lo largo del\(z\) eje positivo, tu dedo índice a lo largo del\(x\) eje positivo y el otro dedo a lo largo del\(y\) eje positivo.
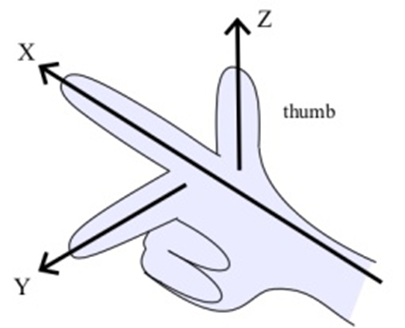
Otras orientaciones de los ejes son posibles y válidas (con el etiquetado adecuado), pero el sistema de la derecha es la orientación más común y es el que generalmente usaremos. Si se usa otra orientación, entonces los ejes se etiquetarán explícitamente.
Cada triple ordenado\((x, y, z)\) especifica la ubicación de un solo punto, y este punto de ubicación se puede trazar ubicando el punto\((x, y, 0)\) en el\(xy\) plano y luego subiendo\(z\) unidades (la ruta roja en la siguiente figura).
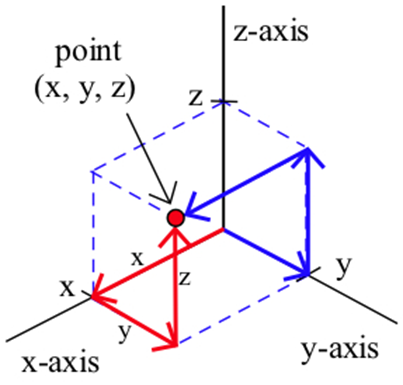
También podríamos llegar al mismo\((x, y, z)\) punto de otras maneras. Por ejemplo, podríamos comenzar por encontrar el punto\((x, 0, z)\) en el\(xz\) plano y luego ir\(y\) unidades paralelas al\(y\) eje -, o por encontrar\((0, y, z)\) en el\(yz\) plano y luego ir\(x\) unidades paralelas al\(x\) eje -eje (el camino azul en la figura anterior).
Trazar las ubicaciones de los puntos
- \( P=(0,3,4) \),
- \( Q=(2,0,4) \),
- \( R=(1,4,0) \),
- \( S=(3,2,1) \), y
- \( T=(-1,2,1) \).
A continuación se muestran los puntos.
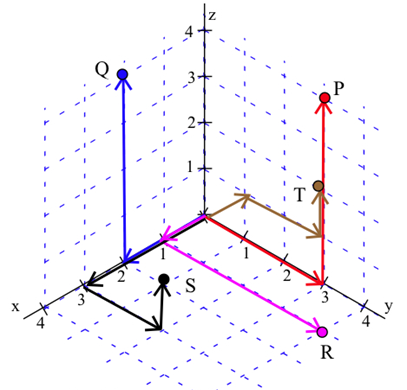
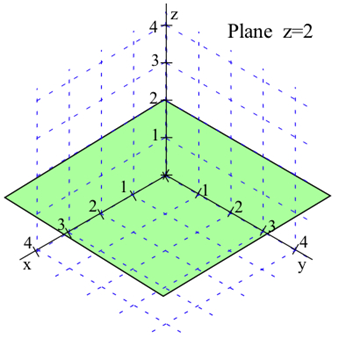
Una vez que podamos ubicar los puntos, podemos comenzar a considerar las gráficas de diversas colecciones de puntos. Por la gráfica de \(z = 2\)
nos referimos a la colección de todos los puntos\((x, y, z)\) que tienen la forma \((x, y, 2)\)
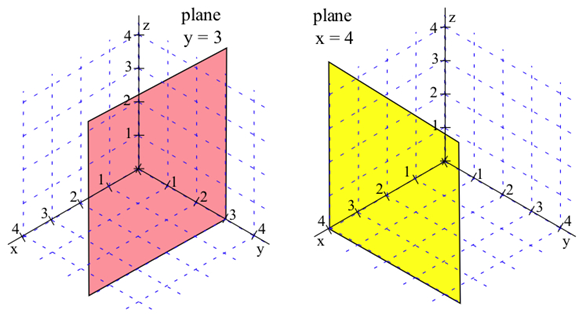
. Dado que no se impone ninguna condición a\(y\) las variables\(x\) y, toman todos los valores posibles. La gráfica de\(z = 2\) es un plano paralelo al\(xy\) plano y 2 unidades por encima del\(xy\) plano. De igual manera, la gráfica de\(y = 3\) es un plano paralelo al\(xz\) plano -plano, y\(x = 4\) es un plano paralelo al\(yz\) plano. (Nota: Los planos se han dibujado como rectángulos, pero en realidad se extienden infinitamente lejos).
Distancia entre puntos
En dos dimensiones podemos pensar en la distancia entre puntos como la longitud de la hipotenusa de un triángulo rectángulo, y eso lleva a la fórmula pitagórica:\[ \text{distance}=\sqrt{\Delta x^2+\Delta y^2}. \nonumber \]
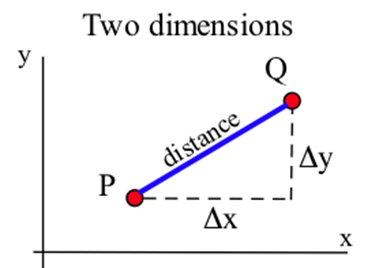
En tres dimensiones también podemos pensar en la distancia entre puntos como la longitud de la hipotenusa de un triángulo rectángulo.
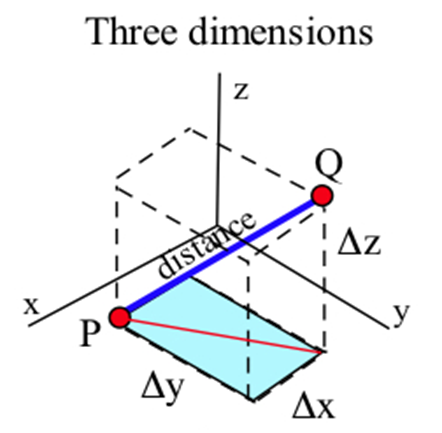
En esta situación los cálculos pueden parecer más complicados, pero son directos y la fórmula final es lo que esperamos que se le dé la fórmula bidimensional:\[ \begin{align*} \text{distance}^2 & = \text{base}^2+\text{height}^2 \\ & = \left(\sqrt{\Delta x^2+\Delta y^2}\right)^2+\Delta z^2 \\ & = \Delta x^2+\Delta y^2+\Delta z^2 \end{align*} \nonumber \] así\[ \text{distance}=\sqrt{\Delta x^2+\Delta y^2+\Delta z^2}. \nonumber \]
Si\(P = (x_1 , y_1 , z_1 )\) and \(Q = (x_2 , y_2 , z_2 )\) are points in space, then the distance between \(P\) and \(Q\) is \[ \begin{align*} \text{distance} & = \sqrt{\Delta x^2+\Delta y^2+\Delta z^2} \\ & = \sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2+\left(z_2-z_1\right)^2} \end{align*} \nonumber \]
El patrón tridimensional es muy similar al patrón bidimensional con la pieza adicional\( \Delta z^2 \).
Encuentra las distancias entre puntos\(A = (1, 2, 3)\) y\(B = (7, 5, –3)\).
Solución
\[ \text{Dist}(A,B)=\sqrt{6^2+3^2+(-6)^2}=\sqrt{36+9+36}=\sqrt{81}=9. \nonumber \]
En dos dimensiones, el conjunto de puntos a una distancia fija de un punto dado es un círculo, y utilizamos la fórmula de distancia para determinar ecuaciones que describen círculos: el círculo con centro (2, 3) y radio 5 viene dado por\((x–2)^2 + (y–3)^2 = 5^2\) o\(x^2 + y^2 – 4x – 6y = 12\).
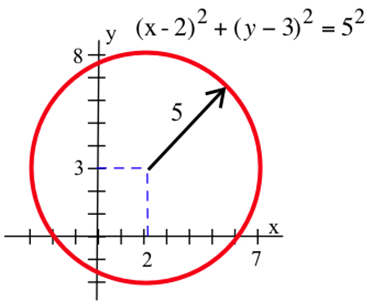
Las mismas ideas funcionan para esferas en tres dimensiones.
El conjunto de puntos\((x, y, z)\) at a fixed distance \(r\) from a point \((a, b, c)\) is a sphere with center \((a, b, c)\) and radius \(r\).
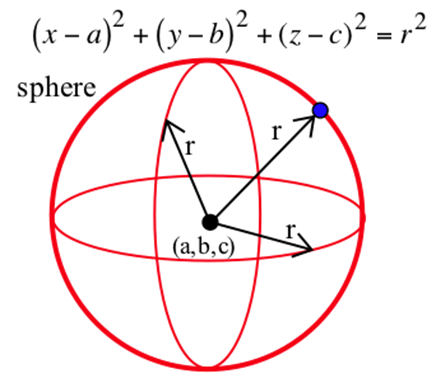
La esfera viene dada por la ecuación\[ (x-a)^2+(y-b)^2+(z-c)^2=r^2. \nonumber \]
Escribe las ecuaciones de una esfera con centro (2, -3, 4) y radio 3.
Solución
La ecuación es\[ (x-2)^2+(y+3)^2+(z-4)^2=3^2. \nonumber \]
Ahora supongamos que queremos graficar una superficie. Podemos pensar en cada entrada\((x,y)\) como una ubicación en el plano, y trazar las\(f(x,y)\) unidades de punto por encima de ese punto. Graficar eso puede ser un desafío. Tenemos algunas opciones:
- Use un programa de computadora (como GeoGebra o Mathematica) para dibujar hermosos dibujos en perspectiva.
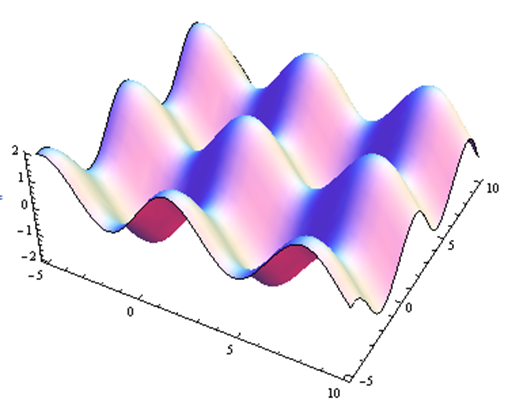
Si tal programa está disponible, entonces esta suele ser la opción más precisa.
- Intenta dibujar un dibujo en perspectiva a mano. Esto es muy desafiante, y por lo general no vale la pena el esfuerzo.
- Usa curvas de nivel para dibujar diagramas de contorno (o mapas de contorno), que es el enfoque en el que nos centraremos aquí. Un diagrama de contorno es como un mapa topográfico: los puntos con la misma elevación (salidas) están conectados con curvas. Cada salida particular se denomina nivel, y estas curvas se denominan curvas de nivel o contornos. Cuanto más cerca estén las curvas entre sí, más pronunciada será esa sección de la superficie. Los mapas topográficos proporcionan a los excursionistas información sobre elevación, pendientes empinadas y poco profundas, picos y valles. Los diagramas de contorno nos dan el mismo tipo de información sobre una función.
A continuación se muestra un diagrama de contorno de la misma superficie que se muestra arriba. Las curvas de nivel son gráficas en el\(xy\) plano de curvas\(f(x, y) = c\) para diversas constantes\(c\).
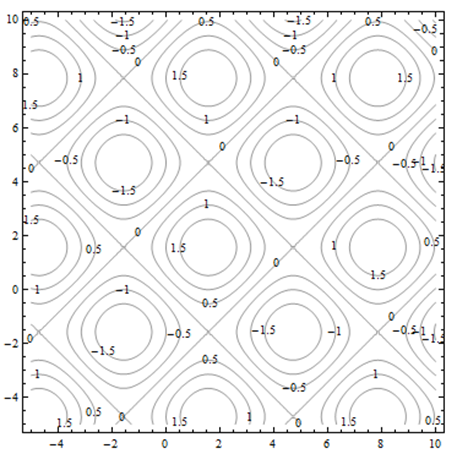
Cada uno de los cuadrados corresponde a uno de los baches en la superficie. Si los contornos son positivos, como se destaca a continuación, la protuberancia está por encima del\(xy\) plano. Si los contornos son negativos, la protuberancia se extiende por debajo del\(xy\) plano.
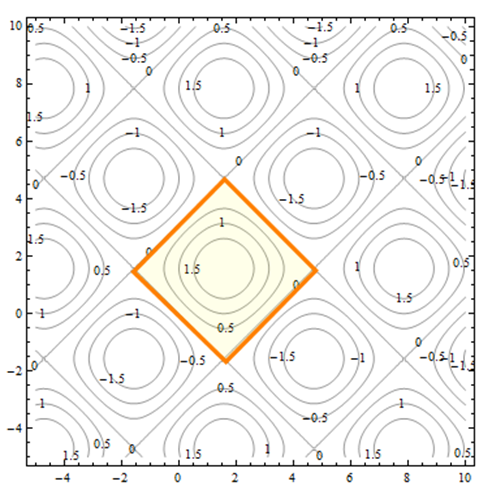
En todas partes en el patrón entrecruzado de líneas diagonales, la altura de la superficie es 0, por lo que la superficie está en el\(xy\) plano. Esta es una característica que no necesariamente habríamos visto cuando miramos el dibujo en perspectiva. Los mapas de contorno pueden ayudarnos a ver las características de la superficie que la gráfica tridimensional no muestra.
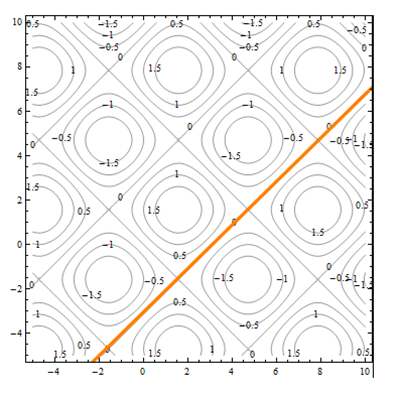
Para entender mejor los diagramas de contorno, supongamos que tenemos una tabla de datos de elevación. Podríamos graficar esto trazando la altura en cada punto y conectando los puntos con curvas suaves, lo que resultaría en algo así como el gráfico mostrado.
Mesa: Alzados dispuestos en una mesa
| \(x\)(etiquetas en la columna izquierda),\(y\) (etiquetas en la fila superior) | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 0 | 1.6 | 1.8 | 2.0 | 2.1 | 2.2 | 2.1 | 2.0 |
| 1 | 2.4 | 2.9 | 3.3 | 3.7 | 5.9 | 3.7 | 3.3 |
| 2 | 3.3 | 4.3 | 5.6 | 6.7 | 7.1 | 6.7 | 5.6 |
| 3 | 3.8 | 5.3 | 7.1 | 9.1 | 9.9 | 9.1 | 7.1 |
| 4 | 3.3 | 4.3 | 5.6 | 6.7 | 7.1 | 6.7 | 5.6 |
| 5 | 2.4 | 2.9 | 3.3 | 3.7 | 5.9 | 3.7 | 3.3 |
| 6 | 1.6 | 1.8 | 2.0 | 2.1 | 2.2 | 2.1 | 2.0 |
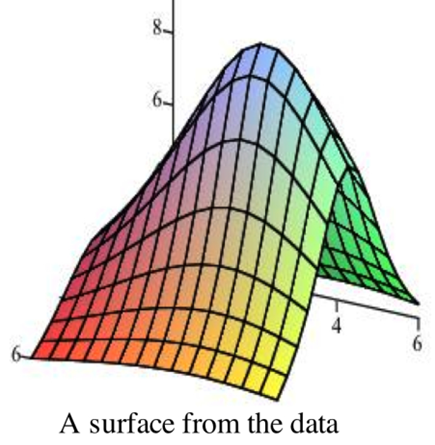
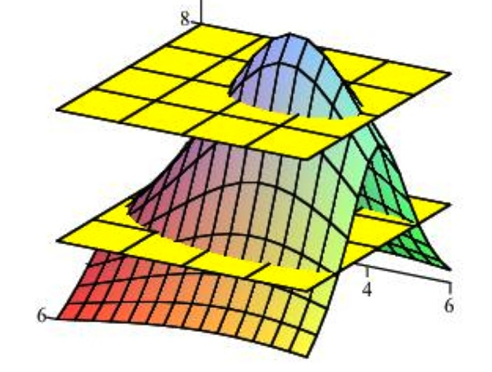
Si cortamos
la superficie de arriba con el plano\(z = 8\), los puntos donde el plano corta la superficie son aquellos puntos donde la elevación de la superficie es de 8 unidades por encima del\(xy\) plano. La siguiente figura muestra la superficie siendo cortada por los planos\(z = 8\) y\(z = 4\). Cortar la superficie a diferentes elevaciones y esbozar las curvas donde el plano interseca la superficie da como resultado la segunda gráfica a continuación.
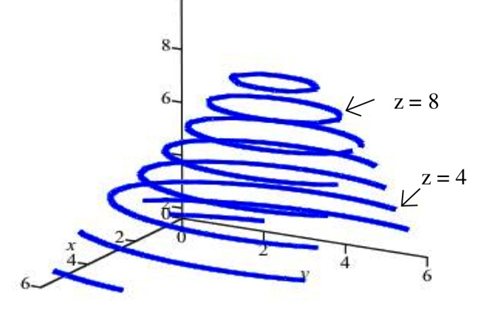
Si movemos todas esas curvas al plano xy (o, de manera equivalente, las vemos directamente desde arriba), el resultado es una gráfica bidimensional de las curvas de nivel de la superficie original. Este es el diagrama de contorno.
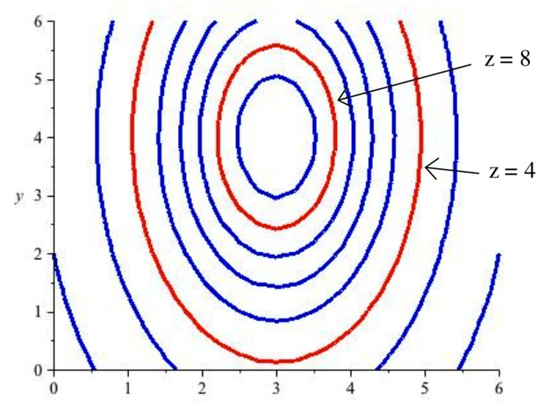
Cree un diagrama de contorno para nuestro ejemplo de alquiler de autos con función de costo\( C(d,m)=40d+0.15m \). Dibuja curvas para cuando el costo sea 0, 100, 200, 300 y 400.
Solución
\( C(d,m)=40d+0.15m=c \)Estableceremos\(c =\) 0, 100, 200, 300 y 400 y dibujaremos las curvas en el\(dm\) plano.
La primera coordenada del par ordenado es\(d\), por lo que el\(d\) eje -eje será horizontal; el\(m\) -eje será vertical. Recuerda que el dominio para esta función es realmente justo donde\(d \geq 0\) y\(m \geq 0\), por lo que solo dibujaremos las curvas en el primer cuadrante.
Cuando\( c=0 \):\[ \begin{align*} C(d,m) & = 40d+0.15m=0 \\ 0.15m & = -40d \\ m & = -\frac{40}{0.15}d\approx -267d \end{align*} \nonumber \]
Esta es la ecuación de una línea, con pendiente alrededor de -267, pasando por el origen. Debido a las restricciones de dominio, la curva
que dibujaremos para este nivel es simplemente el origen. Volviendo a poner esto en el contexto del alquiler de autos, el único punto en el que pagamos $0 por rentar el auto es cuando alquilamos el auto por 0 días y lo manejamos 0 millas —es decir, si no lo alquilamos en absoluto.
Cuando\( c=100 \):\[ \begin{align*} C(d,m) & = 40d+0.15m=100 \\ 0.15m & = -40d+100 \\ m & = -\frac{40}{0.15}d+\frac{100}{0.15}\approx -267d+667 \end{align*} \nonumber \]
Esta es la ecuación de una línea, con pendiente alrededor de -267, y\(d\) -intercepción de aproximadamente 667. Esta sección de esta línea que se encuentra en el primer cuadrante se muestra con 100 etiquetándolo.
Poniendo esto en contexto, cualquier punto de esa línea representa una\((d, m)\) combinación de días y millas que harán que el costo sea exactamente $100. Entonces, por ejemplo — si rentamos el auto por 0 días y lo manejamos 667 millas, nos costará $100. Si alquilamos el auto por 2.5 días y no manejamos millas, nos costará $100.
Continuamos por\(c =\) 200, 300 y 400 y dibujamos las curvas en el plano, dando como resultado el diagrama de contorno que se muestra a la derecha.
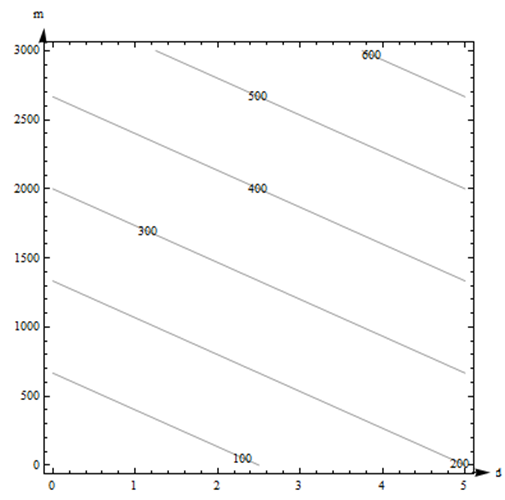
El diagrama de contorno para el costo\(C(d,m)\) en dólares por rentar un auto por\(d\) días y manejarlo\(m\) millas se muestra en el ejemplo anterior. Utilice el diagrama para responder a las siguientes preguntas.
- ¿Cuál es el costo de rentar un auto por 3 días y conducirlo a 200 millas?
- ¿Qué es\(C(100, 4)\)? ¿Qué es\(C(4, 100)\)?
- Supongamos que rentamos el auto por 3 días. ¿Es\(C\) una función creciente de millas?
Solución
- El punto (3, 200) está entre contornos en esta gráfica, por lo que no podemos obtener una respuesta exacta para\(C(3, 200)\). (Pero es típico para una gráfica que tendríamos que estimar). Me parece como si (3, 200) estuviera a medio camino entre los contornos 100 y 200, así que vamos a estimar que\(C(3, 200)\) es alrededor de $150.
Las estimaciones de la gráfica son necesariamente muy aproximadas. La gráfica sólo muestra un poco de información (de esta manera, un diagrama de contorno es como una tabla), así que tenemos que extrapolar en el medio. Pero para la mayoría de las gráficas, en realidad no sabemos qué sucede entre los contornos. Todo lo que sabemos con certeza es que la salida en (3, 200) está entre los dos niveles que vemos. Para este ejemplo de renta de autos, también conocemos una fórmula, y mi tabla mostró esta entrada en particular, así que tenemos otras formas de obtener una mejor respuesta.
- No podemos encontrar (100, 4) en este diagrama, por lo que no podemos hacer una estimación de\(C(100, 4)\) a partir de esta gráfica. (4, 100) se encuentra entre los contornos para 100 y 200. Se ve más cerca de 200, así que vamos a estimar que\(C(4, 100)\) es alrededor de 180 dólares.
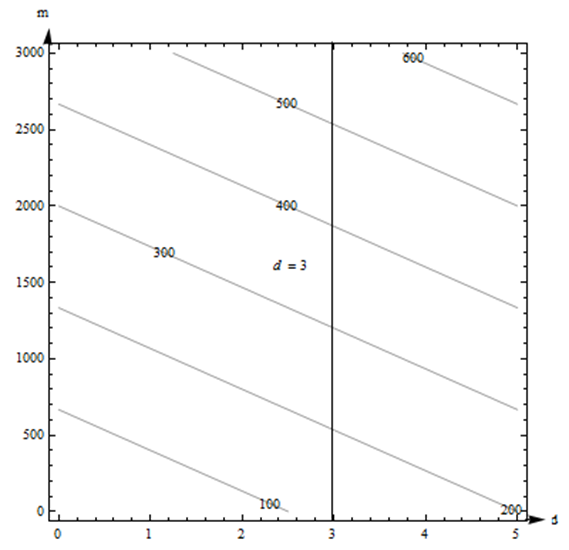
- Si arreglamos\(d = 3\), obtenemos una línea vertical. ¿Qué sucede a medida que\(m\) aumenta esta línea vertical? A\(m\) medida que aumenta, los valores de función mostrados en los contornos aumentan, por lo que\(C\) parece ser una función creciente de millas.
Aquí hay un diagrama de contorno para una función\(g(x,y)\).
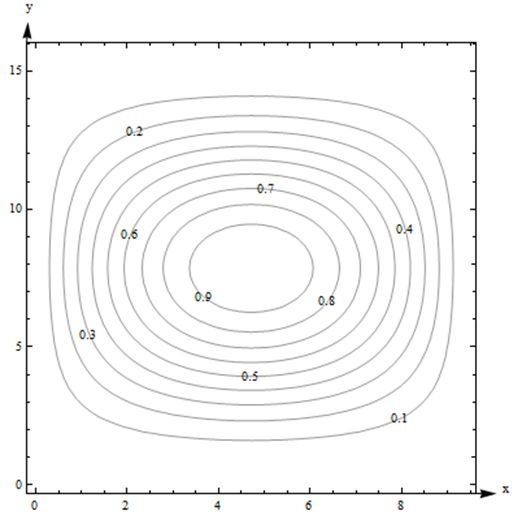
Utilice el diagrama para responder a las siguientes preguntas:
- ¿Qué es\(g(3, 5)\)?
- ¿Cuál es el punto más alto que se muestra en el diagrama? ¿Cuál es el punto más bajo que se muestra?
- Si comienzas en (3, 5) y te diriges en\(x\) dirección positiva, ¿vas primero cuesta arriba o cuesta abajo?
Solución
- \(g(3, 5)\)es 0.6. Podemos decir porque el punto está justo en uno de los contornos, como se ilustra en la imagen de abajo.
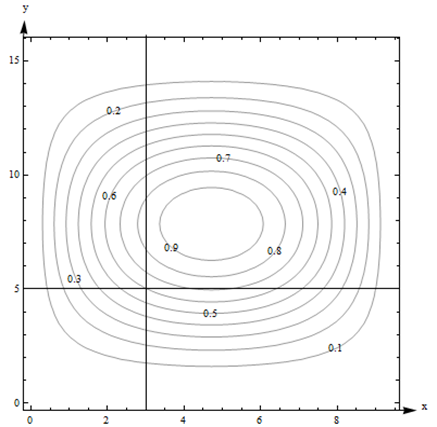
- El contorno más alto mostrado es 0.9, y habría un contorno para 1.0 si la superficie alguna vez hubiera alcanzado ese nivel. No obstante, la altura parece estar aumentando a medida que nos movemos hacia el centro, por lo que parece que\(g\) llega a casi 1 en el centro. El contorno más bajo es 0.1. Pero nuevamente, adivinaremos que la altura sigue disminuyendo, por lo que parece que\(g\) es casi 0 alrededor del exterior.
- Comenzando en el punto (3, 5, 0.6) en la superficie y viajando hacia la derecha a lo largo de la línea horizontal que se muestra en la parte anterior, cruzaríamos el contorno para 0.7 siguiente. Entonces la función aumenta primero (vamos cuesta arriba), y luego vuelve a disminuir.
Nuevamente, recuerda que realmente no sabemos qué pasa entre los contornos. Todo lo que podemos hacer es estimar a partir de la información en la gráfica.
Aquí hay un diagrama de contorno para una función\(F(x,y)\).
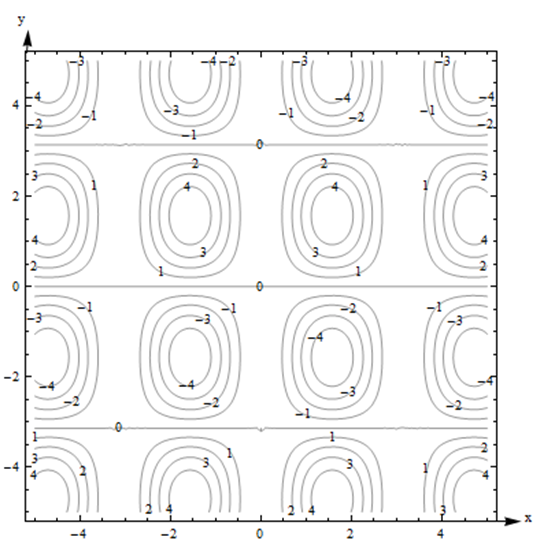
- Describir la forma de la superficie.
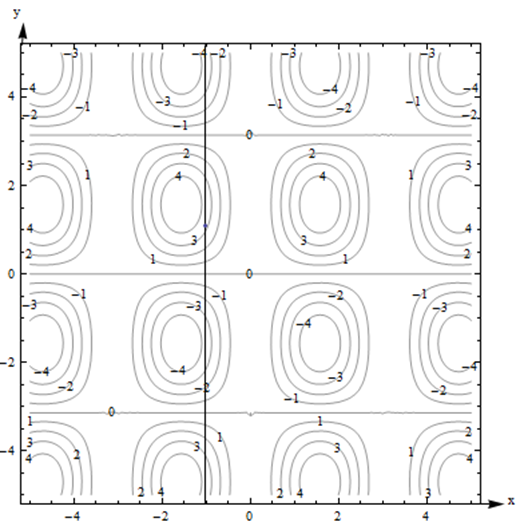
- Supongamos que viaja a lo largo de la superficie en la\(y\) dirección positiva, comenzando en la superficie en el punto por encima (o por debajo) del punto\((x, y) = (-1, 1)\). Describe tu viaje.
Solución
- La superficie es irregular, con protuberancias ovaladas regularmente espaciadas. Observe que algunos de los baches suben (contornos positivos), pero otros bajan. Entre los baches, hay líneas horizontales que están completamente niveladas, con una elevación de 0.
- Parece como si\(F(-1,1)\) se tratara de 3. A medida que nos dirigimos en la\(y\) dirección positiva a lo largo de la línea que se muestra a continuación, primero vamos cuesta arriba, casi a 4, luego comenzamos a ir cuesta abajo. A medida que seguimos yendo hacia el norte, seguimos descendiendo, entrando en el chapuzón, hasta casi -4. Estamos empezando a ir cuesta arriba de nuevo justo cuando dejamos la gráfica.
¿Qué pasa si tienes una función de más de dos variables? Su gráfica será una hipersuperficie. Por ejemplo, la gráfica de una función de cuatro variables será una hipersuperficie en el espacio 5-dimensional. Esto es muy difícil (imposible para la mayoría de nosotros) de visualizar. Incluso los contornos son difíciles de visualizar, en lugar de curvas en el plano, son hipersuperficies en un espacio de 4 dimensiones. Entonces, si tienes más de dos variables, la gráfica no suele ser muy útil.
Funciones de dos variables de la vida real
Mercancías Complementarias y Sustitutas
La demanda de algunos pares de bienes tiene una relación, donde la cantidad demandada por un producto depende de alguna manera de los precios para ambos
Dos bienes son complementarios si un incremento en el precio de cualquiera disminuye la demanda de ambos.
Ejemplos:
- La demanda de autos depende tanto del precio de los autos como del precio de la gasolina.
- La demanda de bollos de hot dog depende tanto del precio de los bollos como del precio de los hot dogs.
Dos bienes son sustitutos si un incremento en el precio de uno aumenta la demanda del otro.
Ejemplo:
- La demanda de la Marca A depende de su precio y también del precio de su principal competidor Marca B. Si la Marca B eleva su precio, los consumidores cambiarán de marca (sustituyen) y la demanda de la Marca A aumentará.
Piense en marcas de refrescos, detergentes o toallas de papel. Un ejemplo tradicional es el café y el té: la idea es que los consumidores simplemente estén buscando una bebida caliente y compren lo que sea más barato. Pero esto siempre me ha parecido a pescado —nunca he conocido a ningún bebedor de café- o té que felizmente cambiaría.
Estas funciones de demanda son funciones de dos variables.
A continuación se detallan las funciones de demanda para dos productos. \(p_1\),\(p_2\)\(q_1\), y\(q_2\) son los precios (en dólares) y cantidades de los Productos 1 y 2:\[ \begin{align*} q_1 & = 200-3p_1-p_2 \\ q_2 & = 150-p_1-2p_2 \end{align*} \nonumber \]
Solución
¿Estos dos productos son bienes complementarios o productos sustitutivos? ¿Cuál es la cantidad demandada por cada uno cuando el precio del Producto 1 es de $20 por artículo y el precio del Producto 2 es de $30 por artículo?
Estos productos son complementarios: un incremento en cualquiera de los dos precios disminuye ambas demandas. Se puede ver eso porque los coeficientes son ambos negativos en cada función de demanda.
Cuando\(p_1 = 20\) y\(p_2 = 30\), tenemos\[ \begin{align*} q_1 & = 200-3(20)-(30)=110 \\ q_2 & = 150-(20)-2(30)=70 \end{align*} \nonumber \] Así se demandan 110 unidades para el Producto 1 y se demandan 70 unidades para el Producto 2 cuando el precio del Producto 1 es de $20 por artículo y el precio del Producto 2 es de $30 por artículo.
Cobb-Douglas Función de Producción
Las funciones de producción se utilizan para modelar la salida total de una empresa para una variedad de entradas (¿no suena esto como una función de varias variables?). Un ejemplo es una función Cobb-Douglas Production:\[ P=AL^{\alpha}K^{\beta} \nonumber \]
En esta función\(P\) está la producción total,\(A\) es una constante,\( \alpha \) y\( \beta \) son constantes entre 0 y 1,\(L\) es la fuerza de trabajo, y\(K\) es el gasto de capital. (Las unidades deben ser bien masajeadas.)
Puedes leer más sobre Cobb-Douglas Funciones de producción en http://en.Wikipedia.org/wiki/Cobb-Douglas. Puede leer sobre otros tipos de funciones de producción en http://en.Wikipedia.org/wiki/Production_function.