4.2: Cálculo de Funciones de Dos Variables
- Page ID
- 110542
Ahora que tienes cierta familiaridad con funciones de dos variables, es momento de empezar a aplicar el cálculo para ayudarnos a resolver problemas con ellas. En el Capítulo 2, aprendimos sobre la derivada para funciones de dos variables. Derivados nos hablaron de la forma de la función, y vamos a encontrar local max y min — queremos poder hacer lo mismo con una función de dos variables.
Primero pensemos. Imagina una superficie, la gráfica de una función de dos variables. Imagina que la superficie es lisa y tiene algunas colinas y algunos valles. Concéntrese en un punto de su superficie. ¿Qué queremos que nos diga el derivado? Debe decirnos qué tan rápido cambia la altura de la superficie a medida que nos movemos... Espera, ¿qué dirección queremos movernos? Esta es la razón por la que las derivadas son más complicadas para funciones de varias variables —hay tantas (de hecho, infinitamente muchas) direcciones que podríamos mover desde cualquier punto.
Resulta que nuestra idea de fijar una variable y ver lo que le sucede a la función a medida que cambia la otra es la clave para extender la idea de derivadas a más de una variable.
Derivadas Parciales
Supongamos que\(z = f(x, y)\) es una función de dos variables.
La derivada parcial de\(f\) con respecto a\(x\) es la derivada de la función\(f(x,y)\) donde pensamos\(x\) como la única variable y actuamos como si fuera\(y\) una constante.
La derivada parcial de\(f\) con respecto a\(y\) es la derivada de la función\(f(x,y)\) donde pensamos\(y\) como la única variable y actuamos como si fuera\(x\) una constante.
El con respecto a\(x\)
o con respecto a
la\(y\) parte es realmente importante — hay que saber y decir en qué variable estás pensando como LA variable.
Geométricamente
Geométricamente la derivada parcial con respecto a\(x\) da la pendiente de la curva a medida que viaja a lo largo de una sección transversal, una curva en la superficie paralela al\(x\) eje -eje. La derivada parcial con respecto a\(y\) da la pendiente de la sección transversal paralela al\(y\) eje.
Notación para la Derivada Parcial
La derivada parcial de\(z = f(x,y)\) con respecto a\(x\) se escribe como\[ f_x(x,y) \nonumber \] o simplemente\[ f_x \quad\text{or}\quad z_x. \nonumber \]
La notación Leibniz es\[ \frac{\partial f}{\partial x} \nonumber \] o\[ \frac{\partial z}{\partial x}. \nonumber \]
Utilizamos una adaptación de la\( \frac{\partial z}{\partial x} \) notación para significar encontrar la derivada parcial de\(f(x,y)\) con respecto a\(x\)
:\[ \frac{\partial}{\partial x}\left(f(x,y)\right)=\frac{\partial f}{\partial x} \nonumber \]
Para estimar una derivada parcial a partir de una tabla o diagrama de curvas de nivel
La derivada parcial con respecto a\(x\) puede aproximarse observando una tasa promedio de cambio, o la pendiente de una línea secante, sobre un intervalo muy pequeño en la\(x\) dirección -dirección (mantener\(y\) constante). Cuanto más pequeño es el intervalo, más cerca está éste de la verdadera derivada parcial.
Para calcular una derivada parcial a partir de una fórmula
Si\(f(x,y)\) se da como fórmula, puede encontrar la derivada parcial con respecto a\(x\) algebraicamente tomando la derivada ordinaria pensando en\(x\) como la única variable (manteniendo\(y\) fija).
Por supuesto, todo aquí funciona de la misma manera si estamos tratando de encontrar la derivada parcial con respecto a\(y\) — solo piensa en\(y\) como tu única variable y actúa como si fuera\(x\) constante.
La idea de una derivada parcial funciona perfectamente bien para una función de varias variables: te enfocas en una variable para que sea LA variable y actúas como si todas las demás variables fueran constantes.
Aquí hay un diagrama de contorno para una función\(g(x,y)\).
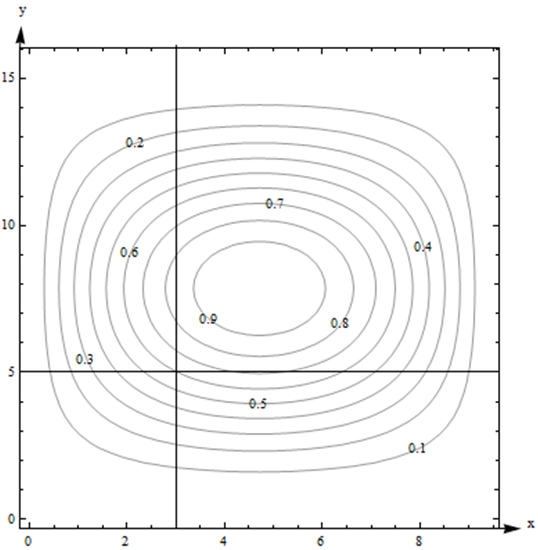
Utilice el diagrama para responder a las siguientes preguntas:
- Estimación\( g_x(3,5) \) y\( g_y(3,5) \).
- ¿Dónde en este diagrama es\( g_x \) mayor? ¿Dónde está el\( g_y \) más grande?
Solución
- \( g_x(3,5) \)significa que estamos pensando en\(x\) como la única variable, así que nos mantenemos\(y\) fijos en\(y = 5\). Eso significa que estaremos mirando a lo largo de la línea horizontal\(y = 5\). Para estimar\(g_x\), necesitamos dos valores de función. (3, 5) se encuentra en la línea de contorno, así que lo sabemos\(g(3, 5) = 0.6\). El siguiente punto a medida que avanzamos hacia la derecha es\(g(4.2,5) = 0.7\).
Ahora podemos encontrar la tasa promedio de cambio:\[ \begin{align*} \text{Average rate of change } & = \frac{\text{(change in output)}}{\text{(change in input)}} \\ & = \frac{\Delta g}{\Delta x}\\ & = \frac{0.7-0.6}{4.2-3}\\ & = \frac{1}{12}\approx 0.083 \end{align*} \nonumber \] Podemos hacer lo mismo yendo al siguiente punto que podamos leer a la izquierda, que es\(g(2.4,5) = 0.5\). Entonces la tasa promedio de cambio es\[ \frac{\Delta g}{\Delta x}=\frac{0.5-0.6}{2.4-3}=\frac{1}{6}\approx 0.167.\nonumber \]
Cualquiera de estos sería una estimación fina de\( g_x(3,5) \) dada la información que tenemos, o podríamos tomar su promedio. Podemos estimar eso\( g_x(3,5)\approx 0.125 \).
Estimar\( g_y(3,5) \) de la misma manera, pero moviéndose en la línea vertical. Usando el siguiente punto arriba, obtenemos la tasa promedio de cambio es\[ \frac{\Delta g}{\Delta y}=\frac{0.7-0.6}{5.8-5}=\frac{1}{8}=0.125.\nonumber \] Usando el siguiente punto hacia abajo, obtenemos\[ \frac{\Delta g}{\Delta y}=\frac{0.5-0.6}{4.5-5}=\frac{1}{5}=0.2.\nonumber \] Tomando su promedio, estimamos\( g_y(3,5)\approx 0.1625 \).
- \( g_x \)significa\(x\) es nuestra única variable, y estamos pensando en ella\(y\) como una constante. Entonces estamos pensando en movernos a través del diagrama en líneas horizontales. \( g_x \)será mayor cuando las curvas de nivel estén más próximas entre sí, es decir, cuando la superficie esté más empinada, entonces el denominador en\( \frac{\Delta g}{\Delta x} \) será pequeño, por lo que\( \frac{\Delta g}{\Delta x} \) será grande. Al escanear la gráfica, podemos ver que las curvas de nivel están más próximas entre sí cuando nos dirigimos hacia la izquierda o hacia la derecha desde aproximadamente (0.5, 8) y (9, 8). Entonces\( g_x \) es mayor en aproximadamente (0.5, 8) y (9, 8). Para\( g_y \), queremos mirar líneas verticales. \( g_y \)es mayor en aproximadamente (5, 3.8) y (5, 12).
Las temperaturas frías se sienten más frías cuando sopla el viento. Windchill es la temperatura percibida y depende tanto de la temperatura real como de la velocidad del viento, ¡una función de dos variables! Puedes leer más sobre windchill en http://www.nws.noaa.gov/om/windchill/. A continuación se muestra una tabla que muestra la temperatura percibida para diversas temperaturas y velocidades del viento.
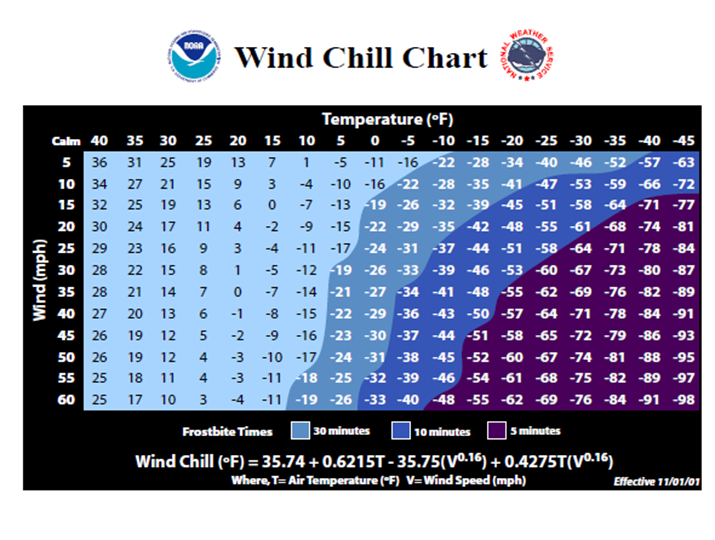
Tenga en cuenta que también incluyen la fórmula, pero para este ejemplo usaremos la información de la tabla.
- ¿Cuál es la temperatura percibida cuando la temperatura real es de 25\(^{\circ}\) F y el viento sopla a 15 millas por hora?
- Supongamos que la temperatura real es de 25\(^{\circ}\) F. ¿Usa la información de la tabla para describir cómo cambiaría la temperatura percibida si la velocidad del viento aumentara de 15 millas por hora?
Solución
- Al leer la tabla, vemos que la temperatura percibida es de 13\(^{\circ}\) F
- Esta es una pregunta sobre una derivada parcial. Estamos manteniendo la temperatura (\(T\)) fija a 25\(^{\circ}\) F, y preguntamos qué sucede a medida que la velocidad del viento (\(V\)) aumenta de 15 millas por hora. Estamos pensando en\(V\) como la única variable, así que queremos\(\text{WindChill}_V = W_V\) cuándo\(T = 25\) y\(V = 15\). Encontraremos la tasa promedio de cambio buscando en la columna dónde\(T = 25\) y dejando que\(V\) aumente, y la usaremos para aproximar la derivada parcial. \[ W_V\approx \frac{\Delta W}{\Delta V}=\frac{11-13}{20-15}=-0.4 \nonumber \]
¿Cuáles son las unidades? \(W\)se mide en\(^{\circ}\) F y\(V\) se mide en mph, por lo que las unidades aquí son\(^{\circ}\) F/mph. Y eso nos permite describir lo que sucede: La temperatura percibida disminuiría en aproximadamente 0.4\(^{\circ}\) F por cada aumento de mph en la velocidad del viento.
Encuentra\( f_x \) y\( f_y \) en los puntos (0, 0) y (1, 1) si\( f(x,y)=x^2-4xy+4y^2 \).
Solución
Para encontrar\( f_x \), tomar la derivada ordinaria de\(f\) con respecto a\(x\), actuando como si fuera\(y\) constante:\[ f_x(x,y)=2x-4y. \nonumber \]
Obsérvese que la derivada del\( 4y^2 \) término con respecto a\(x\) es cero porque es una constante (en lo que\( x \) se refiere).
Del mismo modo,\[ f_y(x,y)=-4x+8y. \nonumber \]
Ahora podemos evaluar estos en los puntos:
\( f_x(0,0)=0 \)y\( f_y(0,0)=0 \); esto nos dice que las secciones transversales paralelas a los ejes\(x\)\(y\) - y - son ambas planas en (0,0).
\( f_x(1,1)=-2 \)y\( f_y(1,1)=4 \); esto nos dice que por encima del punto (1, 1), la superficie disminuye si pasamos a\(x\) valores más positivos y aumenta si pasamos a\(y\) valores más positivos.
Encontrar\( \frac{\partial f}{\partial x} \) y\( \frac{\partial f}{\partial y} \) si\( f(x,y)=\frac{e^{x+y}}{y^3+y}+y\ln(y) \).
Solución
\( \frac{\partial f}{\partial x} \)significa\(x\) es nuestra única variable, estamos pensando en\(y\) como una constante. Entonces sólo encontraremos el derivado ordinario. Desde\(x\) el punto de vista, se trata de una función exponencial, dividida por una constante, con una constante agregada. La constante se saca al frente, la derivada de la función exponencial es lo mismo, y necesitamos usar la regla de la cadena, así multiplicamos por la derivada de ese exponente (que es solo 1):\[ \frac{\partial f}{\partial x}=\frac{1}{y^3+y}e^{x+y}. \nonumber \]
\(\frac{\partial f}{\partial y}\)significa que estamos pensando en\(y\) como la variable, actuando como si fuera\(x\) constante. Desde\(y\) el punto de vista,\(f\) es un cociente más un producto, por lo que necesitaremos la regla del cociente y la regla del producto:\[ \begin{align*} \frac{\partial f}{\partial y} & = \frac{(\ )(\ )-(\ )(\ )}{(\ )^2}+(\ )(\ )+(\ )(\ ) \\ & = \frac{\left( e^{x+y}(1) \right)\left( y^3+y \right)-\left( e^{x+y} \right)\left( 3y^2+1 \right)}{\left( y^3+y \right)^2}+\left( 1 \right)\left( \ln(y) \right)+\left( y \right)\left( \frac{1}{y} \right) \end{align*} \nonumber \]
Encuentra\( f_z \) si\( f(x,y,z,w)=35x^2w-\frac{1}{z}+yz^2 \).
Solución
\( f_z \)significa que actuamos como si fuera\(z\) nuestra única variable, así que actuaremos como si todas las demás variables (\(x\),\(y\), y\(w\)) fueran constantes y tomaremos la derivada ordinaria:\[ f_z(x,y,z,w)=\frac{1}{z^2}+2yz. \nonumber \]
Uso de derivadas parciales para estimar valores de función
Podemos utilizar las derivadas parciales para estimar los valores de una función. La geometría es similar a la aproximación de la línea tangente en una variable. Recordemos el caso de una variable: si\(x\) está lo suficientemente cerca de un punto conocido\(a\), entonces\[ f(x)\approx f(a)+f'(a)(x-a). \nonumber \] En dos variables, hacemos lo mismo en ambas direcciones a la vez:
Para aproximar el valor de\(f(x, y)\), find some point \((a, b)\) where
- \((x, y)\)y\((a, b)\) están cerca, es decir,\(x\) y\(a\) están cerca y\(y\) y\(b\) están cerca.
- Se conocen los valores exactos de\(f(a, b)\) y ambas derivadas parciales ahí.
Entonces\[ f(x,y)\approx f(a,b)+f_x(a,b)(x-a)+f_y(a,b)(y-b). \nonumber \]
Observe que el cambio total en\(f\) se está aproximando sumando los cambios aproximados provenientes de las\(y\) direcciones\(x\) y. Otra forma de ver la misma fórmula:\[ \Delta f\approx f_x\Delta x+f_y\Delta y. \nonumber \]
¿Qué tan cerca está cerca? Depende de la forma de la gráfica de\(f\). En general, cuanto más cerca mejor.
Utilice derivadas parciales para estimar el valor de\( f(x,y)=x^2-4xy+4y^2 \) at (0.9, 1.1).
Solución
Tenga en cuenta que el punto (0.9, 1.1) está cerca de un punto fácil
, (1, 1). De hecho, ya elaboramos las derivadas parciales en (1, 1):\( f_x(x,y)=2x-4y \) así\( f_x(1,1)=-2 \), y\( f_y(x,y)=-4x+8y \) así\( f_y(1,1)=4 \). Eso también lo sabemos\( f(1,1)=1 \).
Entonces,\[ f(0.9,1.1)\approx 1-2(-0.1)+4(0.1)=1.6. \nonumber \]
Tenga en cuenta que en este ejemplo hubiera sido posible simplemente calcular la respuesta exacta:\[ f(0.9,1.1)=(0.9)^2-4(0.9)(1.1)+4(1.1)^2=1.69. \nonumber \] Nuestra estimación no es perfecta, pero está bastante cerca.
Aquí hay un diagrama de contorno para una función\(g(x,y)\). Utilice derivadas parciales para estimar el valor de\(g(3.2, 4.7)\).
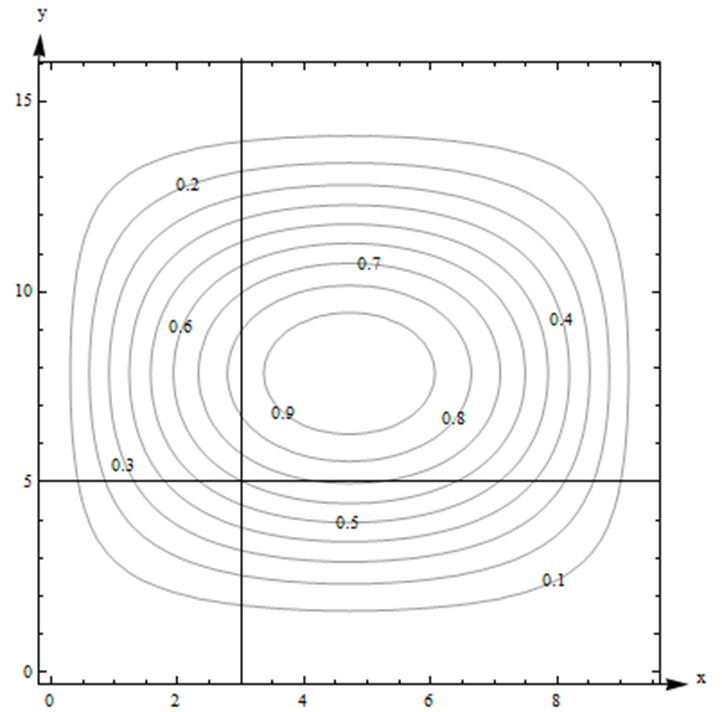
Solución
Este es el mismo diagrama de antes, por lo que ya estimamos el valor de la función y las derivadas parciales en el punto cercano (3,5). \(g(3, 5)\)es 0.6, nuestra estimación de\( g_x(3,5)\approx 0.125 \), y nuestra estimación de\( g_y(3,5)\approx 0.1625 \). Entonces,\[ g(3.2,4.7)\approx 0.6+(0.125)(0.2)+(0.1625)(-0.3)=0.57625. \nonumber \] tenga en cuenta que en este ejemplo no tenemos forma de saber qué tan cerca está nuestra estimación del valor real.


