11.3: Eliminación, gráficos completos y el lema de apretón de manos
- Page ID
- 114413
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
Comenzaremos esta sección introduciendo una operación básica que puede cambiar una gráfica (o un multígrafo, con o sin bucles) en una gráfica más pequeña: la eliminación.
Definición: Eliminación de vértices
Comience con una gráfica (o multígrafo, con o sin bucles)\(G\) con conjunto de vértices\(V\) y bordes\(E\), y algún vértice\(v ∈ V\). Si eliminamos el vértice\(v\) de la gráfica\(G\), la gráfica resultante tiene un conjunto de vértices\(V \setminus \{v\}\) y un conjunto de bordes
\[E \setminus \{e | e \text{ is incident with } v\}.\]
Notación
El gráfico obtenido al eliminar el vértice\(v\) de\(G\) se denota por\(G \setminus \{v\}\). Podemos eliminar más de un vértice; para cualquier conjunto\(S ⊆ V\) de vértices de\(G\), usamos\(G \setminus S\) para denotar la gráfica obtenida al eliminar todos los vértices de\(S\) from\(G\).
El gráfico\(G \setminus \{v\}\) podría ser un multígrafo, pero sólo si\(G\) es. Podría tener bucles, pero sólo si\(G\) tiene bucles.
Si comenzamos con la gráfica
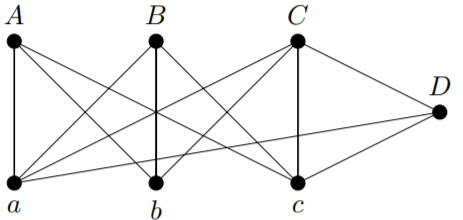
y eliminar el vértice\(D\), después obtenemos la gráfica que se muestra en la Figura 11.2.2.
También podemos eliminar aristas, en lugar de vértices.
Definición: Borrado de bordes
Comience con una gráfica (o multígrafo, con o sin bucles)\(G\) con conjunto de vértices\(V\) y bordes\(E\), y algún borde\(e ∈ E\). Si eliminamos el borde\(e\) de la gráfica\(G\), la gráfica resultante tiene un conjunto de vértices\(V\) y un conjunto de bordes\(E \setminus \{e\}\).
La eliminación de vértices y bordes será muy útil para usar pruebas por inducción en gráficas (y multígrafos, con o sin bucles). Es útil tener terminología para una gráfica que se pueda obtener de otra gráfica eliminando vértices y/o aristas.
Notación
El gráfico obtenido al eliminar el borde\(e\) de\(G\) se denota por\(G \setminus {e}\). Podemos eliminar más de un borde; para cualquier conjunto\(T ⊆ E\) de aristas de\(G\), usamos\(G \setminus T\) para denotar la gráfica obtenida al eliminar todos los bordes de\(T\) desde\(G\).
El gráfico\(G \setminus \{e\}\) podría ser un multígrafo, pero sólo si\(G\) es. Podría tener bucles, pero sólo si\(G\) tiene bucles.
Observe que eliminar los bordes\(\{C, D\}\),\(\{a, D\}\) y\(\{c, D\}\) de la gráfica dibujada arriba, no da como resultado la gráfica que se muestra en la Figura 11.2.2, porque la gráfica que obtenemos al eliminar estos bordes todavía tiene el vértice\(D\) (como un vértice aislado), mientras que la gráfica que se muestra en la Figura 11.2.2 solo tiene los seis vértices\(\{a, b, c, A, B, C\}\).
La eliminación de vértices y bordes será muy útil para usar pruebas por inducción en gráficas (y multígrafos, con o sin bucles). Es útil tener terminología para una gráfica que se pueda obtener de otra gráfica eliminando vértices y/o aristas.
Definición: Subgraph
\(G\)Déjese ser una gráfica. Si se\(H\) puede obtener de\(G\) eliminando vértices y/o aristas, entonces\(H\) es un subgrafo de\(G\). Un subgrafo\(H\) de\(G\) es apropiado si\(H \neq G\).
Ahora definimos una familia muy importante de gráficas, llamadas gráficas completas.
Definición: Gráfica completa
Una gráfica (simple) en la que cada vértice es adyacente a cada otro vértice, se denomina gráfica completa. Si esta gráfica tiene\(n\) vértices, entonces se denota por\(K_n\).
La notación\(K_n\) para una gráfica completa sobre\(n\) vértices proviene del nombre de Kazimierz Kuratowski, un matemático polaco que vivió entre 1896 y 1980. Si bien su principal área de investigación era la lógica, Kuratowski demostró ser un teorema importante que involucra una gráfica completa. Estudiaremos su teorema más adelante en el curso.
Con esta configuración, estamos listos para probar nuestro primer resultado sobre gráficos.
Proposición\(\PageIndex{1}\)
El número de bordes de\(K_n\) es\(\dfrac{n(n−1)}{2} = \binom{n}{2}\)
Presentamos dos pruebas de esta proposición: primero, una prueba combinatoria; luego, una prueba por inducción
- Prueba
-
1) Prueba combinatoria: Una gráfica completa tiene un borde entre cualquier par de vértices. A partir de n vértices, hay\(\binom{n}{2}\) pares que deben estar conectados por un borde para que la gráfica esté completa. Así, hay\(\binom{n}{2}\) bordes en\(K_n\).
Antes de dar la prueba por inducción, mostremos algunas de las pequeñas gráficas completas. En particular, tendremos que tener\(K_1\) en mente ya que será el caso base para nuestra inducción.

2) Prueba Por Inducción: Caso base:\(n = 1\). Como podemos ver arriba, la gráfica\(K_1\) tiene\(0\) aristas. También,
\(\dfrac{n(n−1)}{2} = \dfrac{1(0)}{2} = 0 \)
Entonces la igualdad se sostiene para\(n = 1\). Esto completa la prueba del caso base.
Paso inductivo: Comenzamos con la hipótesis inductiva. \(k ≥ 1\)Sea arbitrario, y supongamos que eso\(K_k\) tiene\(\binom{k}{2}\) aristas.
Queremos deducir que\(K_{k+1}\) tiene\(\binom{k+1}{2}\) aristas. Comience con\(K_{k+1}\), y deje que el número de bordes de esta gráfica sea\(t\). Ahora eliminamos un vértice\(v\) de\(K_{k+1}\). Por la definición de eliminación de vértices, debemos eliminar cada incidente de borde con\(v\). Ya que\(K_{k+1}\) está completo,\(v\) es adyacente a cada otro vértice, por lo que hay\(k\) bordes incidentes con\(v\), y son precisamente estos bordes los que hemos eliminado. Debe haber\(t − k\) bordes restantes.
Observe que la eliminación\(v\) no afecta a los bordes con los que no se producen incidentes\(v\). Por lo tanto, si consideramos dos vértices cualesquiera en la gráfica restante, seguirán siendo adyacentes (ya que estaban adyacentes en\(K_{k+1}\) y el borde entre ellos no se eliminó). Así, la gráfica restante es\(K_k\).
Usando nuestra hipótesis inductiva, sabemos que\(K_k\) tiene\(\dfrac{k(k − 1)}{2}\) bordes. Nosotros hemos demostrado que\(t − k = \dfrac{k(k − 1)}{2}\),
\(t = \dfrac{k(k − 1)}{2} + k = k \left( \dfrac{(k-1)}{2} + 1 \right) = \dfrac{k(k + 1)}{2} = \binom{k+1}{2} \)
que es lo que queríamos deducir. Esto completa la prueba del paso inductivo.
Por el Principio de Inducción Matemática,\(K_n\) tiene\(\binom{n}{2}\) vértices para cada\(n ≥ 1\).
Aunque esta prueba por inducción puede parecer ridículamente larga y complicada en comparación con la prueba combinatoria, sirve como una ilustración relativamente simple de cómo las pruebas por inducción pueden funcionar en gráficas. Esta puede ser una técnica muy poderosa para probar resultados sobre gráficas.
Aquí hay otro resultado que se puede probar usando ya sea una prueba combinatoria, o una prueba por inducción.
Lema\(\PageIndex{1}\): Euler's Handshaking Lemma
Para cualquier gráfica (o multígrafo, con o sin bucles).
\[\sum_{v∈V} d(v) = 2|E| \]
A esto se le llama el lema de apretón de manos porque a menudo se explica usando vértices para representar a las personas, y bordes como apretones de manos entre las personas. En esta explicación, el lema dice que si sumas todas las manos sacudidas por toda la gente, obtendrás el doble del número de apretones de manos que tuvieron lugar. Este es un ejemplo del uso de dos formas de contar pares\((v, e) ∈ V \times E\) tales que\(v\) es incidente con\(e\), una noción que discutimos brevemente cuando introdujimos pruebas combinatorias.
- Prueba
-
Para el lado izquierdo de la ecuación, en cada vértice contamos el número de aristas incidentes con ese vértice. Para obtener el lado derecho de esto, observe que este proceso da como resultado que cada borde haya sido contado exactamente dos veces (una vez en cada uno de sus dos extremos; o, en el caso de un bucle, dos veces en su único vértice extremo ya que ambos extremos están ahí).
Si bien desde la perspectiva correcta el lema del apretón de manos puede parecer obvio, tiene un corolario muy importante y útil.
Corolario\(\PageIndex{1}\)
Cada gráfica tiene un número par de vértices de valencia impar.
- Prueba
-
Dado que la suma de todas las valencias en la gráfica es par (por el lema de apretón de manos de Euler, Lema 11.3.1), el número de summands impares en esta suma debe ser par. Es decir, el número de vértices que tienen valencia impar debe ser par.
Ejercicio\(\PageIndex{1}\)
- Dar una prueba por inducción del lema de apretón de manos de Euler para gráficos simples.
- Empate\(K_7\).
- Mostrar que hay una manera de eliminar un borde y un vértice de\(K_7\) (en ese orden) para que la gráfica resultante esté completa. Mostrar que hay una manera de eliminar un borde y un vértice de\(K_7\) (en ese orden) para que la gráfica resultante no esté completa.
- Demostrar Corolario 11.3.1 por inducción en el número de aristas. (Use la eliminación de bordes y recuerde que el caso base debe ser cuando no hay bordes).
- Use gráficas para dar una prueba combinatoria de que
\(\sum_{i=1}^{k} \binom{n_i}{2} ≤ \binom{n}{2} \)
donde\(n_1, n_2, . . . , n_k\) están los enteros positivos con\(\sum_{i=1}^{k} n_i = n\). ¿En qué circunstancias se sostiene la igualdad?


