11.4: Isomorfismos gráficos

Última actualización
Guardar como PDF

Page ID: 114418

Joy Morris
University of Lethbridge

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

Hay un problema con la forma que hemos definido$K_n$. Se supone que una gráfica consiste en dos conjuntos,$V$ y$E$. A menos que se etiqueten los elementos de los conjuntos, no podemos distinguir entre ellos. Aquí hay dos gráficas,$G$ y$H$:

$clipboard_e12f78e2e42f3751f71037f10f8451ee9.png$

¿Cuál de estas gráficas es$K_2$? No pueden ser los dos$K_2$ ya que no son la misma gráfica, ¿verdad?

La respuesta está en el concepto de isomorfismos. Intuitivamente, las gráficas son isomórficas si son idénticas a excepción de las etiquetas (en los vértices). Recordemos que como se muestra en la Figura 11.2.3, dado que las gráficas están definidas por los conjuntos de vértices y aristas más que por los diagramas, se podrían dibujar dos gráficas isomórficas para que se vean bastante diferentes.

Definición: Isomorfismo

Dos gráficas$G_1 = (V_1, E_1)$ y$G_2 = (V_2, E_2)$ son isomórficas si hay una biyección (una uno-a-uno, sobre mapa)$\varphi$ de$V_1$ a$V_2$ tal que

\[\{v, w\} ∈ E_1 ⇔ \{\varphi(v), \varphi(w)\} ∈ E_2.\]

En este caso, llamamos a$\varphi$ un isomorfismo de$G_1$ a$G_2$.

Notación

Cuando$\varphi$ es un isomorfismo de$G_1$ a$G_2$, abusamos de la notación escribiendo a$\varphi: G_1 → G_2$ pesar de que en realidad$\varphi$ es un mapa en los conjuntos de vértices.

También escribimos$G_1 \cong G_2$ para “$G_1$es isomórfico a”$G_2$.

Entonces un isomorfismo gráfico es una bijección que conserva bordes y no bordes. Si has visto isomorfismos de otras estructuras matemáticas en otros cursos, habrían sido bijecciones que conservaron alguna propiedad o propiedades importantes de las estructuras que estaban mapeando. Para las gráficas, la propiedad importante es qué vértices están conectados entre sí. Si eso se conserva, entonces las redes que se representan son para todos los efectos, las mismas.

Recordemos de$\text{Math } 2000$, una relación se llama relación de equivalencia si es una relación que satisface tres propiedades. Debe ser:

reflexivo (cada objeto debe estar relacionado consigo mismo);
simétrico (si el objeto$A$ está relacionado con el objeto$B$, entonces el objeto también$B$ debe estar relacionado con el objeto$A$); y
transitivo (si el objeto$A$ está relacionado con el objeto$B$ y el objeto$B$ está relacionado con el objeto$C$, entonces el objeto$A$ debe estar relacionado con el objeto$C$).

La relación “es isomórfica con” es una relación de equivalencia en gráficas. Para ver esto, observe que:

Para cualquier gráfica$G$, tenemos$G \cong G$ por el mapa de identidad en los vértices;
Para cualquier gráfica$G_1$ y$G_2$, tenemos

\[G_1 \cong G_2 ⇔ G_2 \cong G_1,\]

ya que cualquier biyección tiene una función inversa que también es una biyección, y desde

\[\{v, w\} ∈ E_1 ⇔ \{\varphi(v), \varphi(w)\} ∈ E_2\]

es equivalente a

\[{\varphi^{−1} (v), \varphi^{−1} (w)} ∈ E_1 ⇔ \{v, w\} ∈ E_2;\]

Para cualquier gráfica$G_1$$G_2$, y$G_3$ con$\varphi_1 : G_1 → G_2$ y$\varphi_2 : G_2 → G_3$ siendo isomorfismos, la composición$\varphi_2 ◦ \varphi_1 : G_1 → G_3$ es una biyección, y

\[\{v, w\} ∈ E_1 ⇔ \{\varphi_1(v), \varphi_1(w)\} ∈ E_2 ⇔ \{\varphi_2(\varphi_1(v)), \varphi_2(\varphi_1(w))\} ∈ E_3,\]

así$G_1 \cong G_3$.

La respuesta a nuestra pregunta sobre las gráficas completas es que dos gráficas completas cualesquiera en$n$ los vértices son isomórficas, así que aunque técnicamente el conjunto de todas las gráficas completas en$2$ vértices es una clase de equivalencia del conjunto de todas las gráficas, podemos ignorar las etiquetas y dar el nombre$K_2$ a todos de las gráficas de esta clase.

Ejemplo$\PageIndex{1}$

Las gráficas$G$ y$H$:

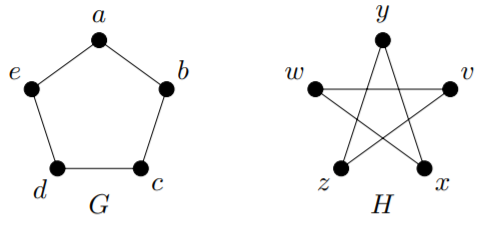
$clipboard_e26629211896e31c00ab2bc8f8d620587.png$

son isomórficos. El mapa$\varphi$ definido por

$\varphi(a) = v$;
$\varphi(b) = z$;
$\varphi(c) = y$;
$\varphi(d) = x$;
$\varphi(e) = w$

Para probar que dos gráficas son isomórficas, debemos encontrar una biyección que actúe como isomorfismo entre ellas. Si queremos demostrar que dos gráficas no son isomórficas, debemos demostrar que ninguna bijección puede actuar como isomorfismo entre ellas.

En ocasiones puede ser muy difícil determinar si dos gráficas son isomórficas o no. Es posible crear gráficas muy grandes que son muy similares en muchos aspectos, pero no son isomórficas. Un enfoque común a este problema ha sido intentar encontrar una “invariante” que distinga entre gráficas no isomórficas. Una “invariante” es una propiedad gráfica que permanece igual para todas las gráficas en cualquier clase de isomorfismo. Así, si puedes encontrar una invariante que sea diferente para dos gráficas, sabes que estas gráficas no deben ser isomórficas. Decimos en este caso que esta invariante distingue entre estas dos gráficas.

A los matemáticos se les han ocurrido muchas, muchas invariantes gráficas. Desafortunadamente, hasta el momento, por cada invariante conocida es posible encontrar dos gráficas que no son isomórficas, sino para las cuales la invariante es la misma. En otras palabras, ninguna invariante conocida distingue entre cada par de gráficas no isomórficas.

Como un aparte para aquellos de ustedes que puedan saber lo que esto significa (probablemente los de la informática), el isomorfismo gráfico es particularmente interesante porque es uno de muy pocos (posiblemente dos, siendo el otro la factorización entera) problemas que se sabe que están en NP pero que no se sabe que estén ni en P, o para ser NP-completo.

Damos algunas invariantes gráficas en la siguiente proposición.

Proposición$\PageIndex{1}$

Si$G_1 \cong G_2$ son gráficas, entonces

$G_1$y$G_2$ tienen el mismo número de vértices;
$G_1$y$G_2$ tienen el mismo número de bordes;
si enumeramos la valencia de cada vértice de$G_1$ y hacemos lo mismo para$G_2$, las listas serán las mismas (aunque posiblemente en un orden diferente). (Dicha lista se llama la secuencia de grados de la gráfica).

Prueba

Ya que$G_1 \cong G_2$, hay un isomorfismo$\varphi : V_1 → V_2$ (donde$V_1$ está el conjunto de vértices de$G_1$ y$V_2$ es el conjunto de vértices de$G_2$). Ya que$\varphi$ es una bijección, debemos tener$|V_1| = |V_2|$.
Ya que\[\{v, w\} ∈ E_1 ⇒ \{\varphi(v), \varphi(w)\} ∈ E_2,\] vemos que por cada borde de$E_1$, hay un borde de$E_2$. Por lo tanto,$|E_2| ≥ |E_1|$. De igual manera, ya que\[\{\varphi(v), \varphi(w)\} ∈ E_2 ⇒ \{v, w\} ∈ E_1,\] vemos eso$|E_1| ≥ |E_2|$. Entonces$|E_1| = |E_2|$.
Si$\varphi(v_1) = v_2$ entonces$d_{G_1} (v_1) = d_{G_2} (v_2)$, porque$u ∼ v_1$ si y solo si$\varphi(u) ∼ v_2$.

Ejemplo$\PageIndex{2}$

La gráfica$G$ del Ejemplo 11.4.1 no es isomórfica a$K_5$, porque$K_5$ tiene$\binom{5}{2} = 10$ bordes por la Proposición 11.3.1, sino$G$ que solo tiene$5$ bordes. Observe que el número de vértices, a pesar de ser una gráfica invariante, no distingue a estas dos gráficas

Las gráficas$G$ y$H$:

$clipboard_e2cabbd6f7bf529447320b27905dd7483.png$

no son isomórficos. Cada uno de ellos tiene$6$ vértices y$9$ aristas. Sin embargo, la gráfica$G$ tiene dos vértices de valencia$2$ ($a$y$c$), dos vértices de valencia$3$ ($d$y$e$), y dos vértices de valencia$4$ ($b$y$f$). En tanto, la gráfica$H$ tiene un vértice de valencia$2$ ($w$), cuatro vértices de valencia$3$ ($u$$x$,$y$, y$z$), y un vértice de valencia$4$ ($v$). Aunque cada una de estas listas tiene los mismos valores ($2$s,$3$ s, y$4$ s), las listas no son las mismas ya que el número de entradas que contienen cada uno de los valores es diferente. En particular, los dos vértices$a$ y$c$ ambos tienen valencia$2$, pero sólo hay un vértice de$H$ (vértice$w$) de valencia dos. Cualquiera$a$ o$c$ podría ser enviado$w$ por un isomorfismo, pero cualquiera de las dos opciones no deja imagen posible para el otro vértice de valencia$2$. Por lo tanto, no es posible un isomorfismo entre estas gráficas.

Observe que las dos gráficas

$clipboard_e5a44714e0bc9bd2ef60cda94142c303d.png$

ambos tienen$6$ vértices y$7$ aristas, y cada uno tiene cuatro vértices de valencia$2$ y dos vértices de valencia$3$. Sin embargo, estas gráficas no son isomórficas. Quizás se pueda pensar en otra gráfica invariante que no sea lo mismo para estas dos gráficas.

Para probar que estas gráficas no son isomórficas, ya que cada una tiene dos vértices de valencia$3$, cualquier isomorfismo tendría que$\{c, f\}$ mapearla a$\{v, z\}$. Ahora bien, cualquier vértice al que se le asigne$u$ debe ser un vecino mutuo de$c$ y$f$ ya que$u$ es un vecino mutuo de$v$ y$z$. Pero$c$ y no tener vecinos mutuos, así que esto no es posible. Por lo tanto, no hay isomorfismo entre estas gráficas.

Un problema natural a considerar es: ¿cuántas gráficas diferentes hay en$n$ los vértices? Si no nos preocupa si las gráficas son isomórficas o no, podríamos tener infinitamente muchas gráficas con solo cambiar las etiquetas en los vértices, y eso no es muy interesante. Para evitar este problema, arreglamos el conjunto de etiquetas que utilizamos. Etiquetar los vértices con los elementos de$\{1, . . . , n\}$. Llamaremos al número de gráficas que encontramos, al número de gráficas etiquetadas en$n$ vértices.

Cualquier borde es un$2$ subconjunto de$\{1, . . . , n\}$. Hay$\binom{n}{2}$ posibles bordes en total. Cualquier gráfica se forma tomando un subconjunto de los$\dfrac{n(n − 1)}{2}$ posibles bordes. En el Ejemplo 4.1.1, aprendimos a contar estos: hay$\dfrac{2n(n−1)}{2}$ subconjuntos

Ejemplo$\PageIndex{3}$

Cuando$n = 1$, tenemos$\binom{1}{2} = 0$, y$2^0= 1$, entonces hay exactamente una gráfica etiquetada en el$1$ vértice. Se ve así:

$clipboard_eb99a858cf7a1c8a30530820931147f9f.png$

Cuando$n = 2$, tenemos$\binom{2}{2} = 1$, y$2^1 = 2$. así que hay exactamente dos gráficas etiquetadas en$2$ los vértices. Se ven así:

$clipboard_e9f05fad25bc025fcb80a512bcbaf8914.png$

Cuando$n = 3$, tenemos$\binom{3}{2} = 3$, y$2^3 = 8$, así hay exactamente ocho gráficas etiquetadas en$3$ vértices. Se ven así:

$clipboard_e8973f7b9ae644505ed2af6acb6d2b3e6.png$

Cuando$n = 4$, tenemos$\binom{4}{2} = 6$, y$2^6 = 64$, así hay exactamente sesenta y cuatro gráficas etiquetadas en$4$ vértices. No intentaremos dibujarlos a todos aquí.

Aunque esa respuesta es cierta hasta donde va, sin duda observarás que aunque estemos usando un conjunto fijo de etiquetas, algunas de las gráficas que hemos contado son isomórficas a otras. Una pregunta más interesante sería, ¿cuántas clases de gráficas de isomorfismo hay en$n$ los vértices? Ya que estamos considerando clases de isomorfismo, las etiquetas que elegimos para los vértices son en gran parte irrelevantes excepto para decirnos qué vértices están conectados a qué otros vértices, si no tenemos diagrama. Así, si estamos dibujando las gráficas, solemos omitir etiquetas de vértice y referirnos a las gráficas resultantes (cada una de las cuales representa una clase de isomorfismo) como sin etiquetar. Entonces la pregunta es, ¿cuántas gráficas sin etiquetar hay en$n$ los vértices?

Podemos elaborar la respuesta a esto para pequeños valores de$n$. A partir de las gráficas etiquetadas sobre$3$ vértices, se puede ver que hay cuatro gráficas sin etiquetar en$3$ vértices. Estos son:

$clipboard_e3cdad5cd93b65564a28c2e1dfc673c54.png$

Hay gráficas$11$ sin etiquetar en cuatro vértices. Desafortunadamente, dado que no existe un algoritmo polinomial-tiempo conocido para resolver el problema del isomorfismo gráfico, determinar el número de gráficas sin etiquetar en$n$ los vértices se vuelve muy difícil a medida que$n$ se agranda, y no se conoce ninguna fórmula general.

Ejercicio$\PageIndex{1}$

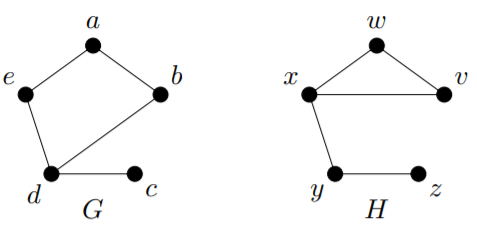
Para cada uno de los siguientes pares de gráficas, encuentra un isomorfismo o prueba que las gráficas no son isomórficas.

1) $clipboard_e8f809d3a59ece3f8496df2d53327cb48.png$

2) $clipboard_ef1fa1fd4749d3261dc9576a38d51f3f1.png$

3)$G_1 = (V_1, E_1)$ y$G_2 = (V_2, E_2)$ con$V_1 = \{a, b, c, d\}$,$V_2 = \{A, B, C, D\}$,$E_1 = \{ab, ac, ad\}$,$E_2 = \{BC, CD, BD\}$.

Ejercicio$\PageIndex{2}$

Dibuja cinco gráficas sin etiquetar en$5$ vértices que no sean isomórficos entre sí.
¿Cuántas gráficas etiquetadas en$5$ vértices tienen$1$ borde?
Cuántas gráficas etiquetadas en$5$ vértices tienen$3$ o$4$ aristas

Search

Text Color

Text Size

Margin Size

Font Type