3.5: Resolver problemas combinatorios recursivamente
- Page ID
- 118565
En esta sección, presentamos ejemplos de problemas combinatorios para los cuales las soluciones se pueden calcular recursivamente. En el Capítulo 9, volvemos a estos problemas y obtenemos soluciones aún más compactas. Nuestro primer problema es uno que se discute en nuestro capítulo introductorio.
Se dibuja una familia de\(n\) líneas en el plano con (1) cada par de líneas cruzando y (2) no tres líneas cruzando en el mismo punto. Dejar\(r(n)\) denotar el número de regiones en las que el plano está dividido por estas líneas. Evidentemente,\(r(1) = 2, r(2) = 4, r(3)=7\) y\(r(4) = 11\). Para determinar\(r(n)\) para todos los enteros positivos, basta con señalar eso\(r(1)=2\), y cuándo\(n>1\),\(r(n) = n+r(n-1)\). Esta fórmula se desprende de la observación de que si etiquetamos las líneas como\(L_1,L_2,...,L_n\), entonces los\(n-1\) puntos en línea\(L_n\) donde cruza las otras líneas de la familia\(L_n\) se dividen en\(n\) segmentos, dos de los cuales son infinitos. Cada uno de estos segmentos está asociado a una región determinada por las primeras\(n−1\) líneas que ahora se ha subdividido en dos, dándonos\(n\) más regiones de las que fueron determinadas por\(n−1\) líneas. Esta situación se ilustra en la Figura 3.4, donde se encuentra la línea que contiene los tres puntos\(L_4\). Las otras líneas lo dividen en cuatro segmentos, que luego dividen regiones más grandes para crear las regiones 1 y 5, 2 y 6, 7 y 8, y 4 y 9.
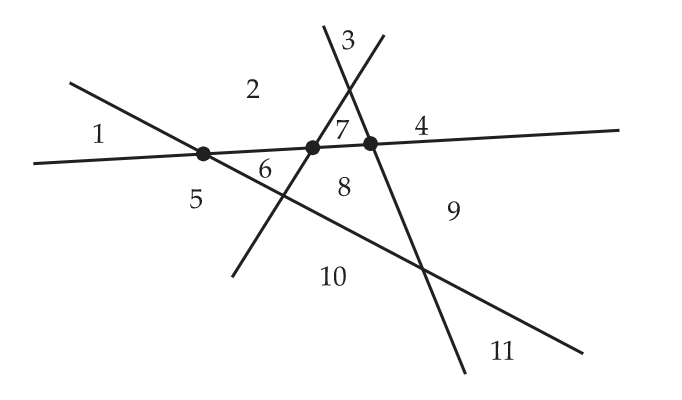
Con la fórmula recursiva, así tenemos\(r(5)=5+11=16, r(6)=6+16=22 and r(7)=7+22=29\). Incluso a mano, no sería tanto problema de calcular\(r(100)\). Podríamos hacerlo antes del almuerzo.
Un\(2 \times n\) tablero de ajedrez será alicatado con rectángulos de tamaño\(2 \times 1\) y\(1 \times 2\). Encuentra una fórmula recursiva para el número\(t(n)\) de inclinaciones. Claramente,\(t(1)=1\) y\(t(2)=2\). Cuando\(n>2\), considere el rectángulo que cubre el cuadrado en la esquina superior derecha. Si es vertical, entonces precediéndolo, tenemos un alicatado de las primeras\(n−1\) columnas. Si es horizontal, entonces también lo es el rectángulo inmediatamente debajo de él, y procediendo a ellos es un alicatado de las primeras\(n−2\) columnas. Esto demuestra que\(t(n)=t(n−1)+t(n−2)\). En particular,\(t(3)=1+2=3, t(4)=2+3=5\) y\(t(5) = 3 + 5 = 8\).
Nuevamente, si nos obligan, podríamos obtener a\(t(100)\) mano, y un sistema de álgebra de computadora podría obtener\(t(1000)\).
Llamar a una cadena ternaria buena si nunca contiene un 2 seguido inmediatamente por un 0; de lo contrario, llámalo malo. Dejar\(g(n)\) ser el número de buenas cadenas de longitud\(n\). Obviamente\(g(1)=3\), ya que todas las cadenas de longitud 1 son buenas. Además,\(g(2)=8\) ya que la única cadena mala de longitud 2 es (2,0). Ahora considere un valor\(n\) mayor a 2.
Dividir el conjunto de buenas cadenas de longitud n en tres partes, de acuerdo con el último carácter. Las buenas cadenas que terminan en 1 pueden ir precedidas por cualquier buena cadena de longitud\(n−1\), por lo que hay\(g(n−1)\) tales cadenas. Lo mismo se aplica para las buenas cuerdas que terminan en 2. Para buenas cuerdas que terminan en 0, sin embargo, hay que tener más cuidado. Podemos preceder al 0 por una buena cadena de longitud\(n−1\) siempre que la cadena no termine en 2. Hay\(g(n−1)\) buenas cuerdas de longitud\(n−1\) y de estas,\(g(n−2)\) terminan exactamente en un 2. Por lo tanto hay\(g(n−1)−g(n−2)\) buenas cadenas de longitud\(n\) que terminan en un 0. De ahí que el número total de buenas cadenas de longitud\(n\) satisfaga la fórmula recursiva\(g(n)=3g(n−1)−g(n−2)\). Así\(g(3)=3 \cdot 8−3=21\) y\(g(4)=3 \cdot 21−8=55\).
Una vez más,\(g(100)\) es factible a mano, mientras que incluso una computadora modesta puede ser engañada para que nos dé\(g(5000)\).
3.5.1 Encontrar los mejores divisores comunes
Hay más carne de la que podrías pensar para el siguiente teorema elemental, que parece simplemente afirmar un hecho que conoces desde segundo grado.
Dejar\(m\) y\(n\) ser enteros positivos. Entonces existen enteros únicos\(q\) y\(r\) para que
\(m=q \cdot n+r\)y\(0≤r<n\).
Llamamos\(q\) al cociente y\(r\) al resto.
- Prueba
-
Resolvemos el reclamo de existencia. La parte de la singularidad es solo álgebra de secundaria. Si el teorema no logra sostenerse, entonces deja\(t\) ser el número entero menos positivo para el cual hay enteros\(m\) y\(n\) con\(m+n=t\), pero no existen enteros\(q\) y\(r\) con\(m=qn+r\) y\(0≤r<n\).
Primero, observamos que\(n \neq 1\), por si\(n=1\), entonces podríamos tomar\(q=m\) y\(r=0\). Además, no podemos tener\(m=1\), porque si\(m=1\), entonces podemos tomar\(q=0\) y\(r=1\). Ahora la sentencia se mantiene para el par\(m−1, n\) por lo que hay enteros\(q\) y\(r\) para que
\(m−1=q \cdot n+r\)y\(0≤r<n\).
Ya que\(r<n\), eso lo sabemos\(r+1≤n\). Si\(r+1<n\), entonces
\(m=q \cdot n+(r+1)\)y\(0≤r+1<n\).
Por otro lado, si\(r+1=n\), entonces
\(m=q \cdot n+(r+1)=nq+n=(q+1)n=(q+1)n+0\).
La contradicción completa la prueba.
Recordemos que un entero\(n\) es un divisor de un entero\(m\) si hay un entero\(q\) tal que\(m=qn\). (Escribimos\(n|m\) y leemos “\(n\)divide\(m\)”.) Un entero\(d\) es un divisor común de enteros\(m\) y\(n\) si\(d\) es un divisor de ambos\(m\) y\(n\). El mayor divisor común de\(m\) y\(n\), escrito\(gcd(m,n)\), es el más grande de todos los divisores comunes de\(m\) y\(n\).
Aquí hay una aplicación particularmente elegante del teorema básico anterior:
Dejar\(m,n\) ser enteros positivos con\(m>n\) y let\(q\) y\(r\) ser los enteros únicos para los cuales
\(m=q \cdot n+r\)y\(0≤r<n\).
Si\(r>0\), entonces\(gcd(m,n)=gcd(n,r)\). Si\(r=0\), entonces\(n\) divide\(m\), y\(gcd(m,n) = n\).
- Prueba
-
Considera la expresión\(m=q \cdot n+r\), que es equivalente a\(m−q \cdot n=r\). Si un número\(d\) es un divisor de\(m\) y\(n\), entonces también se\(d\) debe dividir\(r\). Del mismo modo, si\(d\) es un divisor de\(n\) y\(r\), entonces también se\(d\) debe dividir\(m\).
Aquí hay un fragmento de código que calcula el mayor divisor común de\(m\) y\(n\) cuándo\(m\) y\(n\) son enteros positivos con\(m≥n\). Utilizamos la notación familiar m%n para denotar el resto\(r\) en la expresión\(m=q \cdot n+r\), con\(0 \leq r < n\).
//Código
Siéntase libre de cambiar los valores 12 y 5 anteriores en la celda SueMath en la versión HTML del texto para calcular el divisor más común de algunos otros enteros. ¡Solo recuerda que el código asume\(m≥n\) cuando lo haces!
La desventaja de este enfoque es el uso algo derrochador de la memoria debido a las llamadas a funciones recursivas. No es difícil desarrollar código para computar el mayor divisor común de\(m\) y\(n\) usar solo un bucle, es decir, no hay llamadas recursivas. Con un trabajo extra mínimo, dicho código también se puede diseñar para resolver el siguiente problema de ecuación diofantina:
Dejar\(m, n\), y\(c\) ser enteros positivos. Entonces existen enteros\(a\) y\(b\), no necesariamente no negativos, resolviendo la ecuación diofantina lineal\(am+bn=c\) si y solo si\(c\) es un múltiplo del mayor divisor común de\(m\) y\(n\)
Veamos cómo se puede utilizar el algoritmo euclidiano para escribir\(gcd(m,n)\) en el formulario\(am+bn\)\(a,b \in \mathbb{Z}\) con el siguiente ejemplo.
Encuentra el mayor divisor común\(d\) de 3920 y 252 y encuentra enteros\(a\) y\(b\) tal que\(d = 3920a + 252b\).
- Solución
-
Al resolver el problema, demostramos cómo realizar el algoritmo euclidiano para que podamos encontrar\(a\) y\(b\) trabajando hacia atrás. En primer lugar, observamos que
\(3920=15 \cdot 252+140\).
Ahora el algoritmo euclidiano nos dice eso\(gcd(3920,252)=gcd(252,140)\), así que escribimos
\(252=1 \cdot 140+112\).
Continuando, tenemos\(140=1 \cdot 112+28\) y\(112=4 \cdot 28+0\), entonces\(d=28\).
Para encontrar\(a\) y\(b\), ahora trabajamos hacia atrás a través de las ecuaciones que encontramos antes, “resolviéndolas” para el término restante y luego sustituyendo. Empezamos con
\(28=140−1 \cdot 112\).
Pero lo sabemos\(112=252−1 \cdot 140\), entonces
\(28=140−1(252−1 \cdot 140)=2 \cdot 140−1 \cdot 252\).
Por último\(140=3920−15 \cdot 252\),, así que ahora tenemos
\(28=2(3920−15 \cdot 252)−1 \cdot 252=2 \cdot 3920−31 \cdot 252\).
Por lo tanto\(a=2\) y\(b=−31\).
3.5.2 Clasificación
Uno de los problemas informáticos más comunes y básicos es la clasificación: Dada una secuencia\(a_1,a_2,…,a_n\) de enteros\(n\) distintos, reordenarlos para que estén en orden creciente. Describimos aquí una estrategia recursiva fácil para llevar a cabo esta tarea. Esta estrategia se conoce como Merge Sort, y es uno de varios algoritmos óptimos para ordenar. Los cursos introductorios de informática tratan este tema con mayor profundidad. En nuestro curso, simplemente necesitamos una buena estrategia y merge sort funciona bien para nuestros propósitos.
Para presentar merge sort, primero se debe desarrollar una estrategia para resolver un caso especial del problema de clasificación. Supongamos que tenemos enteros\(s+t\) distintos
\(\{u_0,u_1,…,u_{s−1},v_0,v_1,…,v_{t−1}\}\)
dispuestos como dos listas con\(u_0<u_1< \cdot \cdot \cdot <u_{s−1}\) y\(v_0<v_1< \cdot \cdot \cdot <v_{t−1}\). ¿Cómo fusionamos estas dos secuencias en una única secuencia creciente de longitud\(s+t\)? Imagínese las dos secuencias colocadas en dos líneas horizontales, una inmediatamente debajo de la otra. Entonces deja\(u\) ser el menor número entero en la primera secuencia y\(v\) el menor número entero en la segunda. Por el momento, esto implica eso\(u=u_0\) y\(v=v_0\), pero los enteros se eliminarán de las dos secuencias a medida que se lleve a cabo el proceso. Independientemente, el significado de\(u\) y\(v\) se conservará. También, set\(i=0\). Después tomar\(a_i\) como mínimo de\(u\) y\(v\) y eliminar\(a_i\) de la secuencia en la que se produce. Después aumenta\(i\) en 1 y repite. Aquí hay un fragmento de código para lograr una operación de fusión, con hasta ahora escrito como u [p] y\(v_q\) ahora escrito como v [q].
//Código
Ahora que tenemos una buena estrategia para fusionar, es fácil desarrollar una estrategia recursiva para clasificar. Dada una secuencia\(a_1,a_2,…,a_n\) de enteros\(n\) distintos, establecemos\(s=⌈n/2⌉\) y\(t=⌊n/2⌋\). Entonces vamos\(u_i=a_i\) para\(i=1,2,…,s\) y\(v_j=a_{s+j}\), para\(j=1,2,…,t\). Ordenar las dos subsecuencias y luego fusionarlas. Para un ejemplo concreto, dada la secuencia (2,8,5,9,3,7,4,1,6), nos dividimos en (2,8,5,9,3) y (7,4,1,6). Estas subsecuencias se clasifican (por una llamada recursiva) en (2,3,5,8,9) y (1,4,6,7), y luego se fusionan estas dos secuencias ordenadas.
Para el tiempo de ejecución, si\(S(n)\) es el número de operaciones que se necesita para ordenar una secuencia de n enteros distintos, entonces\(S(2n)≤2S(n)+2n\), ya que claramente toma\(2n\) pasos para fusionar dos secuencias ordenadas de longitud\(n\). Esto lleva al límite\(S(n)<Cnlogn\) para alguna constante positiva\(C\), y en los cursos de informática, aprenderás (aquí es un ejercicio) que esto es óptimo.


