3.4: Coeficientes binomiales revisitados

Última actualización
Guardar como PDF

Page ID: 118556

Mitchel T. Keller & William T. Trotter
Georgia Tech & Morningside College

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

El coeficiente binomial\(\binom{n}{k}\) se definió originalmente en términos de la notación factorial, y con nuestras definiciones recursivas de la notación factorial, también tenemos una definición completa y jurídico-correcta de los coeficientes binomiales. La siguiente fórmula recursiva proporciona un esquema computacional eficiente.

Dejar\(n\) y\(k\) ser enteros con\(0 \leq k \leq n\). Si\(k=0\) o\(k=n\), establecer\(\binom{n}{k} = 1\). Si\(0 <k<n\), establecer

\(\dbinom{n}{k} = \dbinom{n-1}{k-1} + \dbinom{n-1}{k}\).

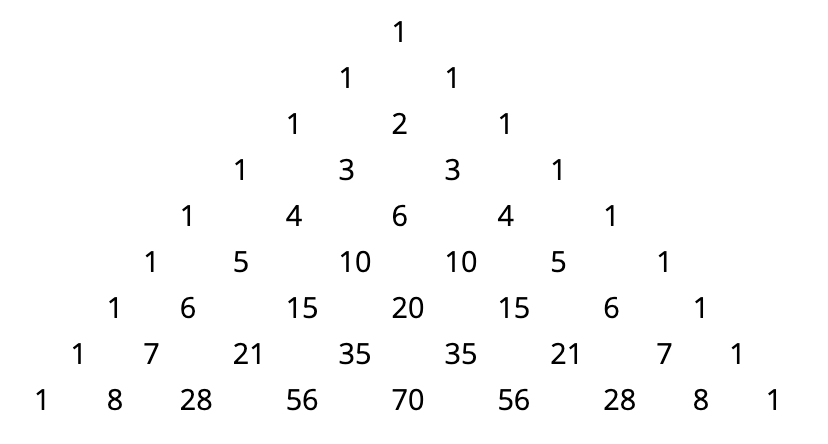
Esta recursión tiene una interpretación combinatoria natural. Ambos lados cuentan el número de subconjuntos\(k\) -element de\(\{1,2,...,n\}\), con el lado derecho primero agrupándolos en aquellos que contienen el elemento\(n\) y luego aquellos que no. La forma tradicional de mostrar esta recursión se muestra en la Figura 3.2. Este patrón se llama “triángulo de Pascal”. Aparte de los 1s en los extremos de cada fila, se determina una entrada del triángulo sumando la entrada a la izquierda y la entrada a la derecha en la fila de arriba.

Screen Shot 2022-02-24 a las 5.20.36 PM.png — Figura **3.2.** Triángulo de Pascal

Xing estaba intrigado por el hecho de que ahora tenía dos formas fundamentalmente diferentes de calcular coeficientes binomiales. Una forma es escribir\(\binom{n}{m} = P(n,m)/(n-m)!\) y simplemente llevar a cabo la aritmética especificada. La segunda forma es usar la recursión del triángulo de Pascal, para que solo estés realizando adiciones. Por lo que experimentó escribiendo un programa de computadora para calcular coeficientes binomiales, usando una biblioteca que trata los enteros grandes como cadenas. ¿Cuál de las dos formas crees que resultó ser más rápida cuando\(n\) digamos fue entre 1800 y 2000 y\(m\) fue alrededor de 800?