5.3: Gráficas eulerianas y hamiltonianas

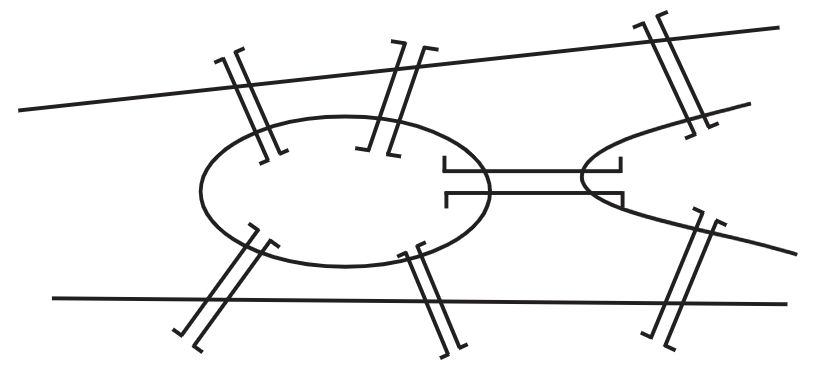
La teoría de grafos es un área de las matemáticas que ha encontrado muchas aplicaciones en una variedad de disciplinas. A lo largo de este texto, nos encontraremos con varios de ellos. Sin embargo, la teoría gráfica remonta sus orígenes a un problema en Königsberg, Prusia (ahora Kaliningrado, Rusia) hace casi tres siglos. El río Pregel pasa por la ciudad, y hay dos grandes islas en medio del canal. Estas islas estaban conectadas al continente por siete puentes como se indica en la Figura 5.12. Se dice que los ciudadanos de Königsberg a menudo se preguntaban si era posible que uno saliera de su casa, pasara por la ciudad de tal manera que cruzara cada puente precisamente una vez, y acabara de nuevo en casa. Leonhard Euler resolvió este problema en 1736 utilizando la teoría de grafos en forma de Teorema 5.13.

Figura 5.12. Los puentes de Königsberg

Dejar\(\textbf{G}\) ser una gráfica sin vértices aislados. Decimos que\(\textbf{G}\) es euleriano siempre que haya una secuencia\((x_0,x_1,x_2,…,x_t)\) de vértices desde\(\textbf{G}\), con repetición permitida, de manera que

1. \(x_0 = x_t\);
2. para cada\(i = 0,1,...,t-1\),\(x_ix_{i+1}\) es una ventaja de\(\textbf{G}\);
3. para cada borde\(e \in E\), hay un entero único\(i\) con\(0 \leq i < t\) para el cual\(e = x_ix_{i+1}\).

Cuando\(\textbf{G}\) es euleriano, una secuencia que satisface estas tres condiciones se denomina circuito euleriano. Una secuencia de vértices\((x_0,x_1,…,x_t)\) se llama circuito cuando satisface sólo las dos primeras de estas condiciones. Tenga en cuenta que una secuencia que consiste en un solo vértice es un circuito. Antes de proceder a la elegante caracterización de Euler de las gráficas eulerianas, usemos SageMath para generar algunas gráficas que son y no son eulerianas.

Ejecute el código a continuación. Se ejecutará hasta que encuentre una gráfica\(\textbf{G}\) que sea euleriana. La salida que se producirá es una lista de los grados de los vértices de la gráfica\(\textbf{G}\) seguida de un dibujo de\(\textbf{G}\).

//código 1

Te animamos a evaluar la ejecución del código anterior varias veces, incluso cambiando el número de vértices y aristas. Si parece estar ejecutando un tiempo de registro, puede ser que hayas hecho que el número de bordes sea demasiado pequeño, así que intenta aumentarlo un poco. ¿Se nota algo sobre los grados de los vértices en las gráficas producidas?

Ahora intentemos encontrar una gráfica\(\textbf{H}\) que no sea euleriana. Nuevamente, la salida es la lista de grados de\(\textbf{H}\) seguido de un dibujo de\(\textbf{H}\).

//código 2

Una cosa que probablemente notaste al ejecutar este segundo bloque de código es que tendía a volver mucho más rápido que el primero. Eso sugeriría que las gráficas no eulerianas superan en número a las gráficas eulerianas. ¿Notó algo diferente sobre los grados de los vértices en estas gráficas en comparación con los que eran eulerianos?

El siguiente teorema elemental caracteriza completamente las gráficas eulerianas. Su prueba da un algoritmo que se implementa fácilmente.

Teorema 5.13

Una gráfica\(\textbf{G}\) es euleriana si y sólo si está conectada y cada vértice tiene grado par.

Prueba

Claramente, se debe conectar una gráfica euleriana. También, si\((x_0,x_1,…,x_t)\) es un circuito euleriano en\(\textbf{G}\), entonces para cada uno\(i=0,1,…,t−1\), podemos ver el borde\(x_ix_{i+1}\) como saliendo\(x_i\) y entrando\(x_{i+1}\). El grado de cada vértice debe ser par, ya que para cada vértice\(x\), el número de aristas que salen\(x\) es igual al número de aristas que entran\(x\). Además, cada incidente de borde con salidas\(x\)\(x\) o entradas\(x\).

Ahora describimos un proceso determinista que (a) encontrará un circuito euleriano, (b) mostrará que la gráfica está desconectada, o (c) encontrará un vértice de grado impar. La descripción se simplifica asumiendo que los vértices en\(\textbf{G}\) han sido etiquetados con los enteros positivos\(1,2,…,n\), donde\(n\) está el número de vértices en\(\textbf{G}\). Además, tomamos\(x_0=1\).

Lanzamos nuestro algoritmo con un circuito trivial\(C\) que consiste en el vértice\(x_0=(1)\). A partir de entonces supongamos que tenemos un circuito parcial\(C\) definido por\((x_0,x_1,…,x_t)\) con\(x_0=x_t=1\). Los bordes de la forma\(x_ix_{i+1}\) han sido atravesados, mientras que los bordes restantes en\(\textbf{G}\) (si los hay) no lo han hecho. Si se cumple la tercera condición para un circuito euler, ya terminamos, por lo que asumimos que no se sostiene.

Luego elegimos el menor número entero\(i\) para el que hay un incidente de borde con el\(x_i\) que aún no se ha atravesado. Si no existe tal entero, ya que hay aristas que aún no han sido atravesadas, entonces hemos descubierto que la gráfica está desconectada. Entonces podemos suponer que el entero\(i\) existe. Set\(u_0=x_i\). Definimos una secuencia\((u_0,u_1,…,u_s)\) recursivamente. Si\(j \geq 0\), establecer

\(N_j = \{y: u_jy\)es un borde en G y aún no ha sido atravesado. \(\}\)

Si\(N_j \neq \0 \), tomamos\(u_{j+1}\) como el número entero menos positivo en\(N_j\). Si\(N_j = 0\), entonces\(j \geq 1\) y tomamos\(s=j\) y detenemos esta subrutina. \

Cuando la subrutina se detiene, consideramos dos casos. Si\(u_0 \ neq u_s, then \(u_0\) y\(u_s\) son vértices de grado impar en\(\textbf{G}\). Entonces nos queda considerar el caso donde\(u_0 = u_s = x_i\). En este caso, simplemente expandimos nuestra secuencia original\((x_0,x_1,...,x_t)\) reemplazando el entero\(x_i\) por la secuencia\((u_0, u_1,...,u_s)\).

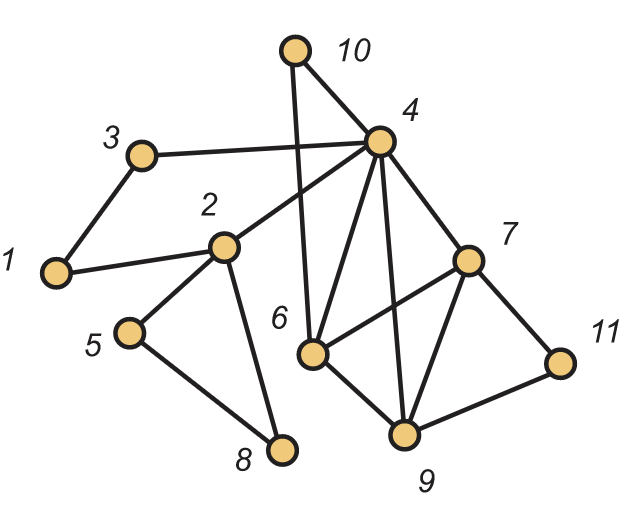
Como ejemplo, considere la gráfica que\(\textbf{G}\) se muestra en la Figura 5.14. Evidentemente, esta gráfica está conectada y todos los vértices tienen grado par. Aquí está la secuencia de circuitos comenzando con el circuito trivial\(C\) que consiste únicamente en el vértice 1.

\ begin {caimán}

C &= (1)\

&= (1,2,4,3,1)\ text {inicio siguiente desde 2}\

&= (1,2,5,8,2,4,3,1)\ text {inicio siguiente desde 4}\

&= (1,2,5,8,2,4,6,7,4,9,9,6,10,4,3,1)\ text {inicio siguiente desde 7}\

&= (1,2,5,8,2,4,6,7,9,11,7,4,9,6,10,4,3,1)\ text {Hecho!!}

\ end {caimán}

Figura 5.14. Una gráfica euleriana

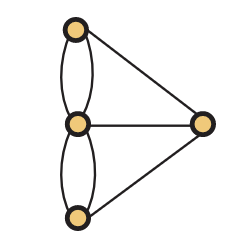
Se debe tener en cuenta que el Teorema 5.13 se mantiene para gráficas loopless en las que se permiten múltiples aristas. Euler utilizó su teorema para mostrar que el multígrafo de Königsberg mostrado en la Figura 5.15, en el que cada masa terrestre es un vértice y cada puente es un borde, no es euleriano, y así los ciudadanos no pudieron encontrar la ruta que deseaban. (Obsérvese que en la Figura 5.15 hay múltiples aristas entre el mismo par de vértices).

Figura 5.15 El multígrafo de los puentes de Königsberg

Se dice que una gráfica\(\textbf{G} = (V,E)\) es hamiltoniana si existe una secuencia\((x_1,x_2,…,x_n)\) para que

1. cada vértice de\(\textbf{G}\) aparece exactamente una vez en la secuencia
2. \(x_1x_n\)es un borde de\(\textbf{G}\)
3. para cada uno\(i = 1,2,...,n-1,x_ix_{i+1}\) es un borde en\(\textbf{G}\).

Tal secuencia de vértices se llama ciclo hamiltoniano.

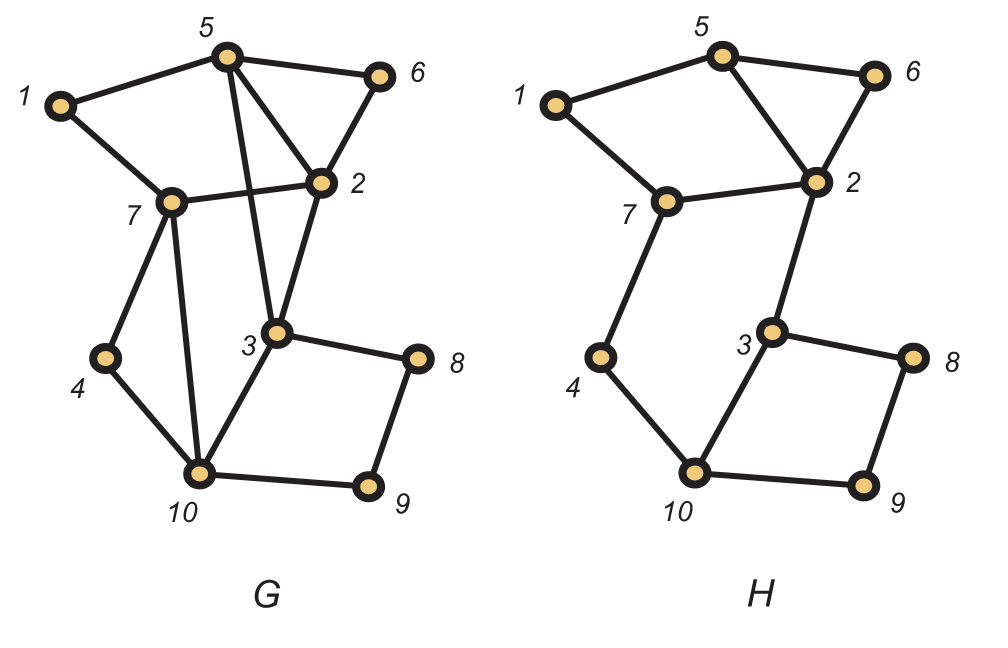
La primera gráfica se muestra en la Figura 5.16 tanto euleriana como hamiltoniana. El segundo es hamiltoniano pero no euleriano.

Figura 5.16. Gráficas eulerianas y hamiltonianas

En la Figura 5.17, mostramos una famosa gráfica conocida como la gráfica Petersen. No es hamiltoniano.

Figura 5.17. La Gráfica Petersen

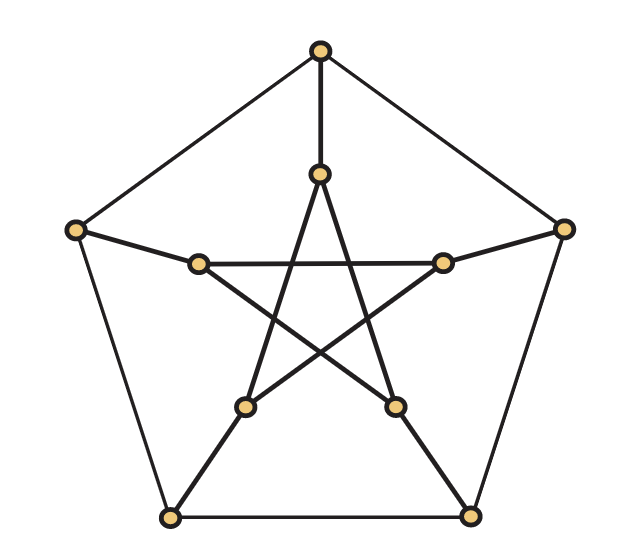
A diferencia de la situación con los circuitos eulerianos, no existe un método conocido para determinar rápidamente si una gráfica es hamiltoniana. Sin embargo, hay una serie de condiciones interesantes que son suficientes. Aquí hay un ejemplo bastante conocido, debido a Dirac.

Teorema 5.18

Si\(\textbf{G}\) es una gráfica sobre\(n\) vértices y cada vértice en\(\textbf{G}\) tiene al menos\(⌈\frac{n}{2}⌉\) vecinos, entonces\(\textbf{G}\) es hamiltoniano.

Prueba

Supongamos que el teorema falla y deja\(n\) ser el número entero menos positivo para el cual existe una gráfica\(\textbf{G}\) en\(n\) vértices para que cada vértice en\(\textbf{G}\) tenga al menos\(⌈n/2⌉\) vecinos, sin embargo no hay ciclo hamiltoniano en\(\textbf{G}\). Claramente,\(n \geq 4\).

Ahora deja\(t\) ser el entero más grande para el cual\(\textbf{G}\) tiene una ruta\(P=(x_1,x_2,…,x_t)\) en\(t\) vértices. Claramente todos los vecinos de ambos\(x_1\) y\(x_t\) aparecen en este camino. Por el principio del hoyo de la paloma, hay algún entero\(i\) con\(1 \leq i < t\) así que\(x_1x_{i+1}\) y\(x_ix_t\) son bordes adentro\(\textbf{G}\). Sin embargo, esto implica que

\(C = (x_1,x_2,x_3,...,x_i,x_t,x_{t-1},x_{t-2},...,x_{i+1})\)

es un ciclo de duración\(t\) en\(\textbf{G}\). A su vez, esto requiere\(⌈n/2⌉<t<n\). Pero si algún vértice no\(y\) está en el ciclo, entonces\(y\) debe tener un vecino encendido\(C\), lo que implica que\(\textbf{G}\) tiene un camino en\(t+1\) vértices. La contradicción completa la prueba.