5.4: Colorear Gráfica

Volvamos ahora al tema del Ejemplo 1.5, asignando frecuencias a las estaciones de radio para que no interfieran. Lo primero que tendremos que hacer es convertir el mapa de las estaciones de radio en una gráfica adecuada, que debería ser bastante natural en esta coyuntura. Definimos una gráfica\(\textbf{G}=(V,E)\) en la que\(V\) se encuentra el conjunto de estaciones de radio y\(xy \in E\) si y sólo si la estación de radio\(x\) y la estación de radio\(y\) están a menos de 200 millas una de la otra. Con esto como nuestro modelo, entonces necesitamos asignar diferentes frecuencias a dos estaciones si sus vértices correspondientes están unidos por un borde. Esto nos lleva a nuestro siguiente tema, colorear gráficos.

Cuando\(\textbf{G}=(V,E)\) es una gráfica y\(C\) es un conjunto de elementos llamados colores, una coloración adecuada de\(\textbf{G}\) es una función\(\phi:V \rightarrow C\) tal que si\(\phi(x) \neq \phi(y)\) siempre\(xy\) es un borde en\(\textbf{G}\). El menor\(t\) para el cual\(\textbf{G}\) tiene una coloración adecuada usando un conjunto\(C\) de\(t\) colores se llama el número cromático de\(\textbf{G}\) y se denota\(\chi(\textbf{G})\). En la Figura 5.19, se muestra una coloración adecuada de una gráfica utilizando 5 colores. Ahora podemos ver que nuestro problema de asignación de radiofrecuencia es la muy estudiada cuestión de encontrar el número cromático de una gráfica apropiada.

Figura 5.19. Una coloración adecuada usando 5 colores

Discusión 5.20.

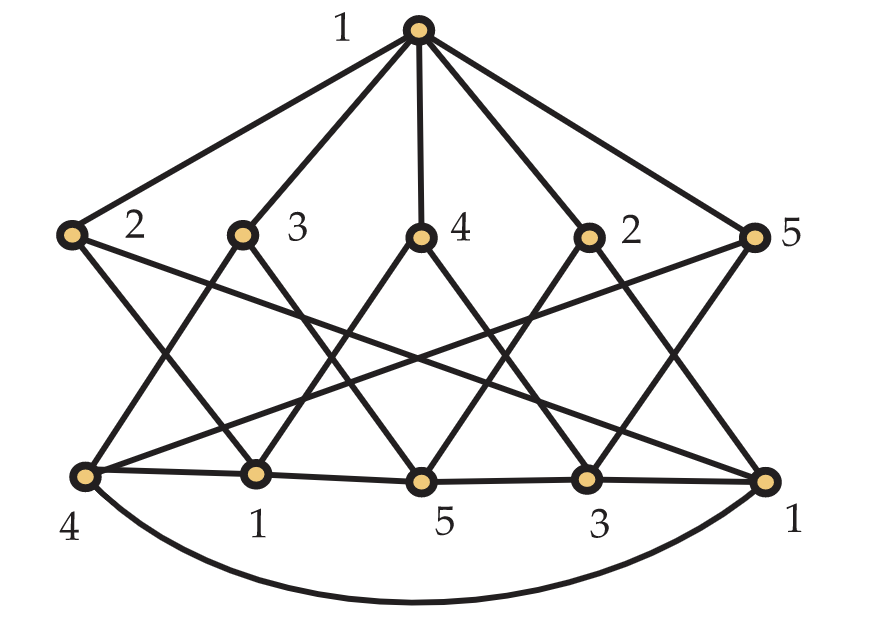
Todos coinciden\(\textbf{G}\) en que la gráfica de la Figura 5.19 tiene número cromático como máximo 5. No obstante, hay un poco de debate sobre si\(\chi(\textbf{G})=5\). Bob imagina que los autores no habrían usado cinco colores si no necesitaban. Carlos dice que está contento de que estén teniendo la discusión, ya que todo lo que tiene una coloración adecuada hace es proporcionarles un límite superior encendido\(χ(\textbf{G})\). Bob ve que la gráfica tiene un vértice de grado 5 y afirma que debe significar\(\chi(\textbf{G})=5\). Alice gime y dibuja una gráfica con 101 vértices, uno de los cuales tiene grado 100, pero con número cromático 2. Bob está conmocionado, pero está de acuerdo con ella. Xing se pregunta si el hecho de que la gráfica no contenga a\(K_3\) tiene alguna relación con el número cromático. Dave tiene prisa por llegar al gimnasio, pero al salir por la puerta dice que pueden obtener un 4-color adecuado con bastante facilidad, entonces\(\chi(\textbf{G}) \leq 4\). El resto decide que es hora de seguir leyendo.

• ¿Qué gráfico dibujó Alice que sorprendió a Bob?
• ¿Qué cambio hizo Dave en la coloración de la Figura 5.19 para obtener una coloración adecuada usando cuatro colores?

5.4.1 Gráficas bipartitas

Una gráfica\(\textbf{G}=(V,E)\) con\(\chi(\textbf{G}) \leq 2\) se llama gráfica de 2 colores. Un par de minutos de reflexión deberían convencerte de que para\(n \geq 2\), el ciclo\(C_{2n}\) con\(2n\) vértices es 2-colorable. Por otro lado, claramente no\(C_3≅K_3\) es 2-colorable. Además, ningún ciclo impar\(C_{2n+1}\) para\(n\geq1\) es 2-colorable. Resulta que la propiedad de contener un ciclo impar es el único impedimento para ser 2-colorable, lo que significa que reconocer gráficas de 2 colores es fácil, como muestra el siguiente teorema.

Teorema 5.21

Una gráfica es 2 -colorable si y sólo si no contiene un ciclo impar.

Prueba

Dejar\(\textbf{G}=(V,E)\) ser una gráfica de 2 colores cuya función de coloración\(V\) se divide como\(A \bigcup B\). Dado que no hay aristas entre vértices en el mismo lado de la partición, cualquier ciclo en\(\textbf{G}\) debe alternar vértices entre\(A\) y\(B\). Para completar el ciclo, por lo tanto, el número de vértices en el ciclo desde\(A\) debe ser el mismo que el número de\(B\), lo que implica que el ciclo tiene una longitud par.

Ahora supongamos que\(\textbf{G}\) no contiene un ciclo impar. Tenga en cuenta que podemos suponer que\(\textbf{G}\) está conectado, ya que cada componente puede ser coloreado individualmente. La distancia\(d(u,v)\) entre vértices\(u,v \in V\) es la longitud de un camino más corto de\(u\) a\(v\), y por supuesto\(d(u,u)=0\). Fijar un vértice\(v_0 \in V\) y definir

\(A = \{v \in V: d(u_0,v)\)es par} y\(B=\{v \in V: d(v_0,v)\) es impar}.

Afirmamos que colorear los vértices de\(A\) con el color 1 y los vértices de\(B\) con el color 2 es una coloración adecuada. supongamos que no. Entonces sin pérdida de generalidad, hay vértices\(x,y \in A\) tales que\(xy \in E\). Ya que\(x,y \in A\),\(d(v_0,x)\) y\(d(v_0,y)\) son ambos parejos. Let

\(v_0,x_1,x_2,...,x_n = x\)

y

\(v_0,y_1,y_2,...,y_m = y\)

ser caminos más cortos de\(v_0\) a\(x\) y\(y\), respectivamente. Si\(x_1 \neq y_j\) por todos\(1 \leq i \leq n\) y\(1 \leq j \leq m\), entonces desde\(m\) y\(n\) son ambos parejos,

\(v_0,x_1,x_2,...,x_n = x, y=y_m,y_{m-1},...,y_2,y_1,v_0\)

es un ciclo impar en\(\textbf{G}\), lo cual es una contradicción. Así, debe haber\(i,j\) tal que\(x_i=y_j\), y podemos tomar\(i,j\) lo más grande posible. (Es decir, después\(x_i=y_j\), los dos caminos no se cruzan de nuevo.) Por lo tanto,

\(x_i,x_{i+1},...,x_n = x, y = y_m, y_{m-1},...,y_j = x_i\)

es un ciclo en\(\textbf{G}\). ¿Cuántos vértices hay en este ciclo? Un conteo rápido muestra que tiene

\(n-(i-1)+m-(j-1)-1 = n+m - (i+j)+1\)

vértices. Sabemos que n y m son pares, y notamos que\(i\) y\(j\) son ambos pares o ambos impares, ya que\(x_i=y_j\) y los vértices de subíndice impar de nuestro camino pertenecen\(B\) mientras que aquellos con subíndices pares pertenecen a\(A\). Así,\(i+j\) es par, así\(n+m−(i+j)+1\) es extraño, dando una contradicción.

Una gráfica\(\textbf{G}\) se llama gráfica bipartita cuando hay una partición del vértice\(V\) en dos conjuntos\(A\) y de\(B\) manera que las subgráficas inducidas por\(A\) y\(B\) son gráficas independientes, es decir, ningún borde de\(\textbf{G}\) tiene ambos de sus puntos finales en\(A\) o en\(B\). Evidentemente, las gráficas bipartitas son de 2 colores. Por otro lado, cuando se desconecta una gráfica de 2 colores, hay más de una forma de definir una partición adecuada del vértice establecida en dos conjuntos independientes.

Los gráficos bipartitos se utilizan comúnmente como modelos cuando hay dos tipos distintos de objetos que se están modelizando y las conexiones solo se permiten entre dos objetos de diferentes tipos. Por ejemplo, por un lado, enumere a los candidatos que asistan a una feria de carreras y por otro lado enumere los puestos disponibles. Los bordes pueden corresponder naturalmente a parejas candidato/posición que vinculan a una persona con una responsabilidad que es capaz de manejar.

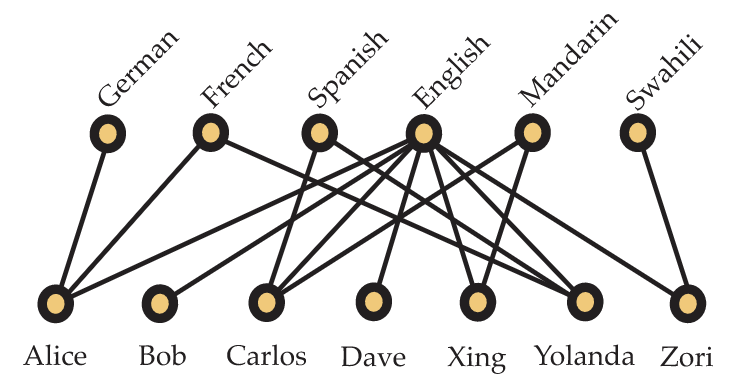
Como segundo ejemplo, se podría utilizar una gráfica bipartita para visualizar los idiomas hablados por un grupo de estudiantes. Los vértices de un lado serían los alumnos con las lenguas listadas en el otro lado. Tendríamos entonces una ventaja\(xy\) cuando el estudiante\(x\) hablaba el idioma\(y\). Un ejemplo concreto de esta gráfica para nuestro grupo favorito de estudiantes se muestra en la Figura 5.22, aunque Alice no está tan segura de que debería haber una arista que conecte a Dave y al inglés.

Figura 5.22. Una gráfica bipartita

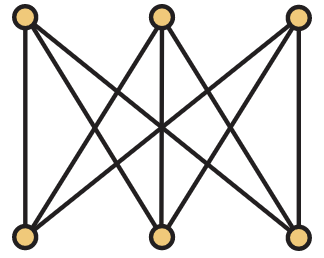
Una clase especial de gráficas bipartitas que merece mención es la clase de gráficas bipartitas completas. La gráfica bipartita completa\(K_{m,n}\) tiene un vértice establecido\(V=V_1 \bigcup V_2\) con\(|V_1|=m\) y\(|V_2|=n\). Tiene un borde\(xy\) si y solo si\(x \in V_1\) y\(y \in V_2\). La gráfica bipartita completa\(K_{3,3}\) se muestra en la Figura 5.23.

Figura 5.23. La gráfica bipartita completa\(K_{3,3}\)

5.4.2 Cliques y Número Cromático

Una camarilla en una gráfica\(\textbf{G}=(V,E)\) es un conjunto\(K \subset V\) tal que la subgrafía inducida por\(K\) es isomórfica a la gráfica completa\(K_{|K|}\). Equivalentemente, podemos decir que cada par de vértices en\(K\) son adyacentes. El tamaño máximo de camarilla o número de camarilla de una gráfica\(\textbf{G}\), denotado\(ω(\textbf{G})\), es el más grande\(t\) para el que existe una camarilla\(K\) con\(|K|=t\). Por ejemplo, la gráfica de la Figura 5.14 tiene la camarilla número 4 mientras que la gráfica de la Figura 5.19 tiene el tamaño máximo de camarilla 2.

Por cada gráfica\(\textbf{G}\), es obvio que\(\chi(\textbf{G})≥ω(\textbf{G})\). Por otro lado, la desigualdad puede estar lejos de ser apretada. Antes de mostrar lo malo que puede ser, necesitamos introducir una versión más general del Principio de Agujero Paloma. Considera una función\(f:X \rightarrow Y\) con\(|X|=2|Y|+1\). Ya que\(|X|>|Y|\), el Principio de Agujero Paloma como se afirma en la Proposición 4.1 sólo nos dice que hay distintos\(x,x′ \in X\) con\(f(x)=f(x′)\). No obstante, podemos decir más aquí. Supongamos que cada elemento de\(Y\) tiene como máximo dos elementos de\(X\) mapeado a él. Después sumando el número de elementos de\(X\) basado en cuántos se mapean a cada elemento de solo\(Y\) permitiría\(X\) tener (como máximo)\(2|Y|\) elementos. Así, debe haber\(y \in Y\) para que haya tres elementos distintos\(x,x′,x″ \in X\) con\(f(x)=f(x′)=f(x″)=y\). Este argumento generaliza para dar la siguiente versión del Principio de Agujero Paloma:

Proposición 5.24. Principio de Agujero de Paloma Generalizado

Si\(f:X \rightarrow Y\) es una función y | (|X|≥ (m−1) |Y|+1\), entonces existe un elemento\(y \in Y\) y elementos distintos\(f(x_i)=y\) para\(x_1,…,x_m \in X\) que para\(i = 1,...,m\).

Ahora estamos preparados para presentar la siguiente proposición mostrando que el número de camarilla y el número cromático no necesitan estar en absoluto cerca. Damos dos pruebas. El primero es el trabajo de J. Kelly y L. Kelly, mientras que el segundo se debe a J. Mycielski.

Proposición 5.25.

Para cada\(t \geq 3\), existe una gráfica\(\textbf{G}_t\) para que\(\chi(\textbf{G}_t)=t\) y\(ω(\textbf{G}_t) = 2\).

Prueba

Se procede por inducción en\(t\). Para\(t=3\), tomamos\(G_3\) para ser el ciclo\(C_5\) en cinco vértices. Ahora supongamos que para algunos\(t \geq 3\), hemos determinado la gráfica\(G_t\). Supongamos que\(G_t\) tiene\(n_t\) vértices. Etiquetar los vértices de\(G_t\) as\(x_1,x_2,…,x_{n_t}\). Construir de\(G_{t+1}\) la siguiente manera. Comience con un conjunto independiente\(I\) de cardinalidad\(t(n_t−1)+1\). Por cada subconjunto\(S\) de\(I\) con\(|S|=n_t\), etiquetar los elementos de\(S\) como\(y_1,y_2,…,y_{n_t}\). Para este subconjunto\(n_t\) de elementos en particular, adjunte una copia de\(G_t\) con\(y_i\) adyacente a\(x_i\) for\(i=1,2,…,n_t\). Los vértices en copias de\(G_t\) para distintos subconjuntos de\(n_t\) elementos de no\(I\) son adyacentes, y un vértice en\(I\) tiene como máximo un vecino en una copia particular de\(G_t\).

Para ver eso\(ω(G_{t+1})=2\), bastará con argumentar que no\(G_{t+1}\) contiene triángulo (\(K_3\)). Dado que\(G_t\) está libre de triángulos, cualquier triángulo en\(G_{t+1}\) debe contener un vértice de\(I\). Dado que ninguno de los vértices de\(I\) son adyacentes, cualquier triángulo en\(G_{t+1}\) contiene solo un punto de\(I\). Dado que cada vértice de\(I\) es adyacente a como máximo un vértice de cualquier copia fija de\(G_t\), si\(y \in I\) es parte de un triángulo, los otros dos vértices deben provenir de distintas copias de\(G_t\). Sin embargo, los vértices en diferentes copias de no\(G_t\) son adyacentes, entonces\(ω(G_{t+1})=2\). Observe que\(\chi(G_{t+1}) \geq t\) ya\(G_{t+1}\) contiene\(G_t\). Por otro lado,\(\chi(G_{t+1}) \leq t+1\) ya que podemos usar\(t\) colores en las copias de\(G_t\) y un nuevo color en el conjunto independiente\(I\). Para ver eso\(\chi(G_{t+1})=t+1\), observe que si usamos solo\(t\) colores, entonces por el Principio de Agujero Paloma generalizado, hay un subconjunto\(n_t\) -elemento\(I\) en el que todos los vértices tienen el mismo color. Entonces este color no se puede usar en la copia de la\(G_t\) cual se adjunta a ese subconjunto\(n_t\) -elemento.

Prueba

De nuevo empezamos con\(G_3\) como el ciclo\(C_5\). Como antes suponemos que hemos construido para algunos\(t \geq 3\) una gráfica\(G_t\) con\(ω(G_t)=2\) y\(\chi(G_t)=t\). Nuevamente, etiquetar los vértices de\(G_t\) as\(x_1,x_2,…,x_{n_t}\). Para construir\(G_{t+1}\), ahora comenzamos con un conjunto independiente\(I\), pero ahora solo\(I\) tiene\(n_t\) puntos, que etiquetamos como\(y_1,y_2,…,y_{n_t}\). Luego agregamos una copia de\(G_t\) con\(y_i\) adyacente a\(x_j\) si y solo si\(x_i\) es adyacente a\(x_j\). Finalmente, adjunte un nuevo vértice\(z\) adyacente a todos los vértices en\(I\).

Claramente,\(ω(G_{t+1})=2\). También,\(\chi(G_{t+1}) \geq t\), ya que contiene\(G_t\) como subgrafo. Además\(\chi(G_{t+1}) \leq t+1\), ya que podemos colorear\(G_t\) con colores de\(\{1,2,…,t\}\), usar color\(t+1\) en el conjunto independiente\(I\), y luego asignar color 1 al nuevo vértice\(z\). Eso lo afirmamos de hecho\(\chi(G_{t+1} )=t+1\). Supongamos que no. Entonces debemos tener\(\chi(G_{t+1})=t\). Dejar\(\phi\) ser una coloración adecuada de\(G_{t+1}\). Sin pérdida de generalidad,\(\phi\) utiliza los colores en\(\{1,2,…,t\}\) y\(\phi\) asigna color\(t\) a\(z\). Entonces considere el conjunto no vacío\(S\) de vértices en la copia de\(G_t\) a la que\(\phi\) asigna color\(t\). Para cada\(x_i\) entrada\(S\), cambie el color encendido para\(x_i\) que coincida con el color asignado\(y_i\) por\(\phi\), que no puede ser\(t\), como\(z\) está coloreado\(t\). Lo que resulta es una correcta coloración de la copia de\(G_t\) con solo\(t−1\) colores ya que\(x_i\) y\(y_i\) son adyacentes a los mismos vértices de la copia de\(G_t\). La contradicción lo demuestra\(\chi (G_{t+1}) =t+1\), como se afirma.

Dado que una camarilla 3 parece un triángulo, la Proposición 5.25 a menudo se afirma como “Existen gráficas sin triángulos con gran número cromático”. Como ilustración de la construcción en la prueba de Mycielski, nuevamente nos referimos a la Figura 5.19. El gráfico que se muestra es\(G_4\). Volveremos al tema de las gráficas con gran número cromático en la Sección 11.6 donde mostramos que hay gráficas con gran número cromático las cuales carecen no solo de camarillas de más de dos vértices sino también ciclos de menos de\(g\) vértices para cualquier valor de\(g\). En otras palabras, ¡hay una gráfica\(\textbf{G}\) con\(\chi(G)=10^6\) pero ningún ciclo con menos de\(10^{10}\) vértices!

5.4.3 ¿Podemos Determinar el Número Cromático?

Supongamos que se le da una gráfica\(\textbf{G}\). Está empezando a parecer que no es fácil encontrar un algoritmo que responda a la pregunta “\(\chi(G) \leq t\)¿Es?” Es fácil verificar un certificado (una coloración adecuada usando como máximo t colores), pero ¿cómo podrías encontrar un color adecuado, sin mencionar uno con el menor número de colores? De igual manera para la pregunta “¿Es? \(ω(G) \geq k\)?” , es fácil verificar un certificado. Sin embargo, encontrar una camarilla máxima parece ser un problema muy difícil. Por supuesto, dado que la brecha entre\(\chi(G)\) y\(ω(G)\) puede ser arbitrariamente grande, poder encontrar un valor no ayudaría (generalmente) a encontrar el valor del otro. No se conoce ningún algoritmo polinomial-tiempo para ninguno de estos problemas, y muchos creen que no existe tal algoritmo. En esta subsección, observamos un enfoque para encontrar el número cromático y vemos un caso en el que sí funciona de manera eficiente.

Una forma algorítmica muy ingenua de acercarse a la coloración gráfica es el algoritmo First Fit, o “codicioso”. Para este algoritmo, arregle un orden del conjunto de vértices\(V=\{v_1,v_2,…v_n\}\). Definimos la función de coloración\(\phi\) un vértice a la vez en orden creciente de subíndice. Comenzamos con\(\phi(v_1)=1\) y luego definimos\(\phi(v_{i+1})\) (asumiendo\(v_1,v_2,…,v_i\) que los vértices han sido coloreados) para que sea el color entero menos positivo que no se haya usado ya en ninguno de sus vecinos en el conjunto\(\{v_1,...v_i\}\).

Figura 5.26. Dos ordenamientos de los vértices de una gráfica bipartita.

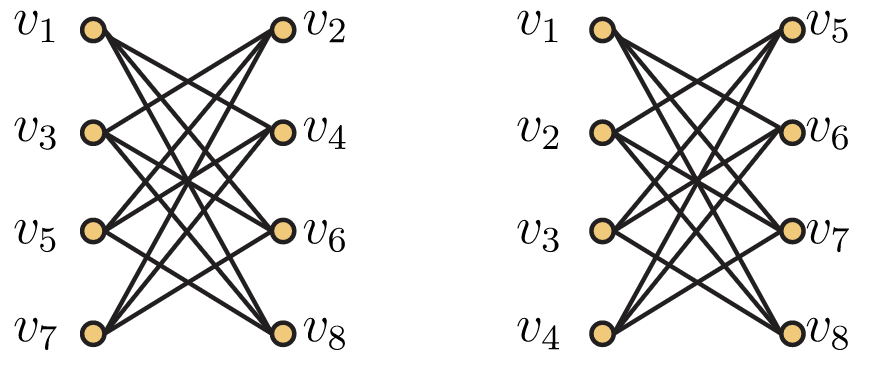
La Figura 5.26 muestra dos ordenamientos diferentes de la misma gráfica. El ejercicio 5.9.24 demuestra que el orden de\(V\) es vital para la capacidad del algoritmo First Fit para colorear\(\textbf{G}\) usando\(\chi(G)\) colores. En general, encontrar un orden óptimo es tan difícil como colorear\(\textbf{G}\). Por lo tanto, este algoritmo muy sencillo no funciona bien en general. Sin embargo, para algunas clases de gráficas, existe un orden “natural” que conduce a un rendimiento óptimo de First Fit. Aquí hay uno de esos ejemplos, uno que volveremos a estudiar en el siguiente capítulo en un contexto diferente.

Dada una familia indexada de conjuntos\(\mathcal{F}=\{S_{\alpha}:\alpha \in V\}\), nos asociamos con\(\mathcal{F}\) una gráfica\(\textbf{G}\) definida de la siguiente manera. El conjunto de vértices de\(\textbf{G}\) es el conjunto\(V\) y los vértices\(x\) y\(y\) en\(V\) son adyacentes en\(\textbf{G}\) si y solo si\(S_x \cap S_y \neq \emptyset\). Llamamos a\(\textbf{G}\) una gráfica de intersección. Es fácil ver que cada gráfica es una gráfica de intersección (¿Por qué? ), por lo que tiene sentido restringir los conjuntos a los que pertenecen\(\mathcal{F}\). Por ejemplo, llamamos a\(\textbf{G}\) una gráfica de intervalos si es la gráfica de intersección de una familia de intervalos cerrados de la línea real\(\mathbb{R}\). Por ejemplo, en la Figura 5.27, mostramos una colección de seis intervalos de la línea real a la izquierda. A la derecha, mostramos el gráfico de intervalos correspondiente que tiene un borde entre vértices\(x\) y\(y\) si y sólo si intervalos\(x\) y\(y\) solapamiento.

Figura 5.27. Una colección de intervalos y su gráfica de intervalos

Teorema 5.27

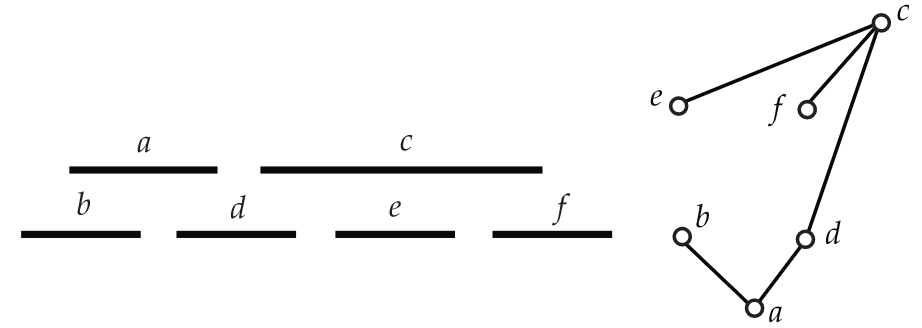
Si\(G=(V,E)\) es un gráfico de intervalos, entonces\(\chi(G) = ω(G)\).

Prueba

Para cada uno\(v \in V\), deja\(I(v)=[a_v,b_v]\) ser un intervalo cerrado de la línea real para que\(uv\) sea un borde en\(\textbf{G}\) si y solo si\(I(u) \cap I(v) \neq \emptyset\). Ordene el conjunto de vértices\(V\) como\(\{v_1,v_2,…v_n\}\) tal que\(a_1 \leq a_2 \leq \cdot \cdot \cdot \leq a_n\). (Los lazos pueden romperse arbitrariamente.) Aplique el algoritmo de coloración First Fit a\(\textbf{G}\) con este orden encendido\(V\). Ahora, cuando el algoritmo de coloración First Fit colorea\(v_i\), todos sus vecinos han dejado el punto final como máximo\(a_i\). Ya que son vecinos de\(v_i\), sin embargo, sabemos que sus puntos finales correctos son todos al menos\(a_i\). Así,\(v_i\) y sus vecinos previamente coloreados forman una camarilla. De ahí que\(v_i\) sea adyacente a lo sumo\(ω(G)−1\) otros vértices que ya han sido coloreados, por lo que cuando el algoritmo colorea\(v_i\), habrá un color de\(\{1,2,…,ω(G)\}\) no estar ya en uso en sus vecinos. El algoritmo asignará\(v_i\) el color más pequeño de ese tipo. Por lo tanto, nunca necesitamos usar más que\(ω(G)\) colores, entonces\(\chi(G) = ω(G)\).

Se dice que una gráfica\(\textbf{G}\) es perfecta si\(\chi(H)=ω(H)\) para cada subgrafía inducida\(H\). Dado que una subgrafía inducida de una gráfica de intervalos es una gráfica de intervalos, el Teorema 5.28 muestra que las gráficas de intervalos son perfectas. El estudio de las gráficas perfectas se originó en conexión con la teoría de las redes de comunicaciones y ha demostrado ser un área importante de investigación en teoría de grafos desde hace muchos años.