5.6: Contar árboles etiquetados
- Page ID
- 118420
¿Cuántos árboles hay con conjunto de vértices\([n]=\{1,2,…,n\}\)? \(T_n\)Sea este número. Porque\(n=1\), claramente hay un solo árbol. También, para\(n=2\), sólo hay un árbol, que es isomórfico a\(K_2\). En la determinación\(T_3\),, finalmente tenemos algo de trabajo que hacer; sin embargo, no hay mucho, ya que todos los árboles en 3 vértices son isomórficos a\(P_3\). Así, hay árboles\(T_3=3\) etiquetados en 3 vértices, correspondientes a los cuales vértice es el de grado 2. Cuando\(n=4\), podemos comenzar contando el número de árboles no isomórficos y considerar dos casos dependiendo de si el árbol tiene un vértice de grado 3. Si hay un vértice de grado 3, el árbol es isomórfico a\(K_{1,3}\) o no tiene un vértice de grado tres, en cuyo caso es isomórfico a\(P_4\), ya que debe haber precisamente dos vértices de grado 2 en dicha gráfica. Hay cuatro etiquetas por\([4]\) para\(K_{1,3}\) (elija el vértice del grado tres). ¿Para cuántos\([4]\) etiquetados hay\(P_4\)? Hay\(C(4,2)\) formas de elegir las etiquetas\(i,j\) dadas a los vértices de grado 2 y dos formas de seleccionar una de las etiquetas restantes a hacer adyacentes\(i\). Así, hay 12 formas de etiquetar\(P_4\) por\([4]\) y así\(T_4 = 16\).
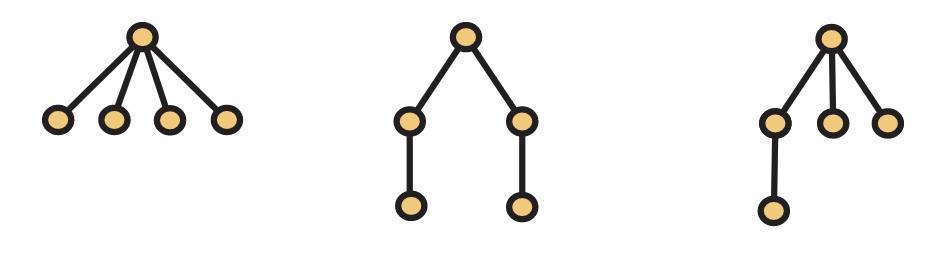
A este punto, parece que tal vez hay un patrón que se forma. Quizás sea el caso que para todos\(n \geq 1, T_n=n^{n−2}\). De hecho, este es el caso, pero veamos cómo funciona\(n=5\) antes de probar el resultado en general. ¿Cuáles son los árboles no isomórficos en cinco vértices? Bueno, ahí está\(K_{1,4}\) y\(P_5\) seguro, y también está el tercer árbol que se muestra en la Figura 5.38. Después de pensarlo uno o dos minutos, deberías poder convencerte de que estas son todas las posibilidades. ¿Cuántos etiquetados por\([5]\) cada uno de estos tiene? Hay 5 para\(K_{1,4}\) ya que hay 5 formas de elegir el vértice de grado 4. Para\(P_5\), hay 5 formas de elegir el vértice medio del camino,\(C(4,2)=6\) formas de etiquetar los dos vértices restantes de grado 2 una vez que se etiqueta el vértice medio, y luego 2 formas de etiquetar los vértices del grado 1. Esto da 60 etiquetas. Para el último árbol, hay 5 formas de etiquetar el vértice del grado 3,\(C(4,2)=6\) formas de etiquetar las dos hojas adyacentes al vértice del grado 3, y 2 formas de etiquetar los dos vértices restantes, dando 60 etiquetas. Por lo tanto,\(T_5 = 125 = 5^3 = 5^{5-2}\).
Resulta que de hecho estamos en el camino correcto, y ahora nos propusiremos probar lo siguiente:
El número\(T_n\) de árboles etiquetados en los\(n\) vértices es\(n^{n-2}\).
Este resultado suele ser referido como la Fórmula de Cayley, aunque los resultados equivalentes fueron probados anteriormente por James J. Sylvester (1857) y Carl W. Borchardt (1860). La razón por la que el nombre de Cayley se fija con mayor frecuencia a este resultado es que fue el primero en declararlo y probarlo en terminología teórica gráfica (en 1889). (Aunque se podría argumentar que Cayley realmente solo lo demostró\(n=6\) y luego afirmó que fácilmente podría extenderse para todos los demás valores de\(n\), y si tal extensión realmente puede suceder está abierto a algún debate.) Cayley's Formula tiene muchas pruebas diferentes, la mayoría de las cuales son bastante elegantes. Si te interesan las presentaciones de varias pruebas, te animamos a leer el capítulo sobre la Fórmula de Cayley en Pruebas de EL LIBRO de Aigner, Ziegler y Hofmann, que contiene cuatro pruebas diferentes, todas utilizando diferentes técnicas de prueba. Aquí damos una quinta prueba, debido a Prüfer y publicada en 1918. Curiosamente, a pesar de que la prueba de Prüfer llegó después de que se estableciera gran parte de la terminología de la teoría gráfica, parecía desconocerla y trabajó en el contexto de las permutaciones y su propia terminología, a pesar de que su enfoque incluye claramente las ideas de la teoría gráfica. Utilizaremos una técnica recursiva para encontrar una biyección entre el conjunto de árboles etiquetados en\(n\) vértices y un conjunto natural de tamaño\(n^{n−2}\), el conjunto de cadenas de longitud de\(n−2\) donde provienen los símbolos de la cadena\([n]\).
Definimos un algoritmo recursivo que toma un árbol\(T\) sobre\(k \geq 2\) vértices etiquetados por elementos de un conjunto\(S\) de enteros positivos de tamaño\(k\) y devuelve una cadena de longitud\(k−2\) cuyos símbolos son elementos de\(S\). (El conjunto\(S\) suele ser\([k]\), pero para definir un procedimiento recursivo, necesitamos permitir que sea un conjunto arbitrario de enteros\(k\) positivos.) Esta cadena se llama el código Prüfer del árbol\(T\). Dejemos que prüferprüfer (\(T\)) denote el código Prüfer del árbol\(T\), y si\(v\) es una hoja de\(T\), vamos a\(T−v\) denotar el árbol obtenido de\(T\) quitando\(v\) (es decir, el subgrafo inducido por todos los demás vértices). Entonces podemos definir prüferprüfer (\(T\)) recursivamente mediante el siguiente procedimiento.
- Si\(T≅K_2\), devuelve la cadena vacía.
- De lo contrario, deja\(v\) ser la hoja de\(T\) con la etiqueta más pequeña y deja que\(u\) sea su vecino único. Deja\(i\) ser la etiqueta de\(u\). Retorno (\(i\), prüfer (\(T - v\))).
Antes de usar los códigos de Prüfer para probar la Fórmula de Cayley, tomemos un momento para asegurarnos de entender cómo se calculan dado un árbol. Considera el árbol de 9 vértices\(T\) en la Figura 5.41.
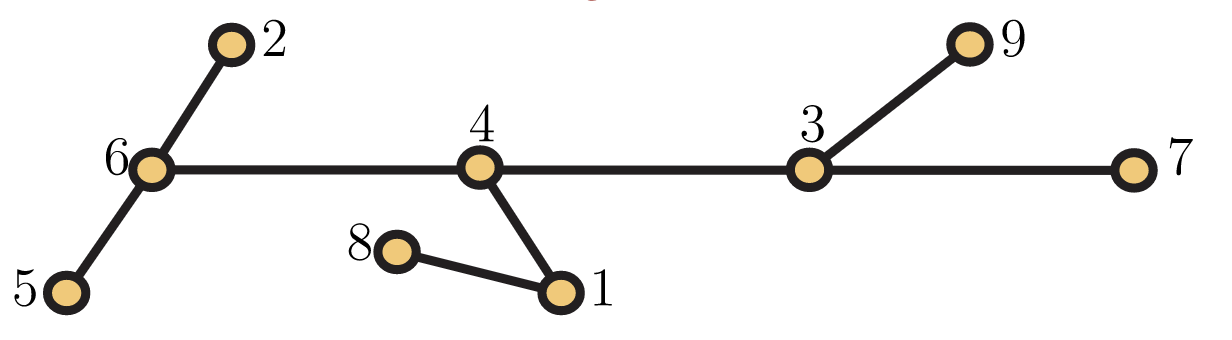
¿Cómo calculamos prüfer (\(T\))? Ya que\(T\) tiene más de dos vértices, usamos el segundo paso y encontramos que\(v\) es el vértice con etiqueta 2 y\(u\) es el vértice con etiqueta 6, así prüfer (\(T\)) =( 6, prüfer (\(T−v\))). La gráfica\(T−v\) se muestra en la Figura 5.42.
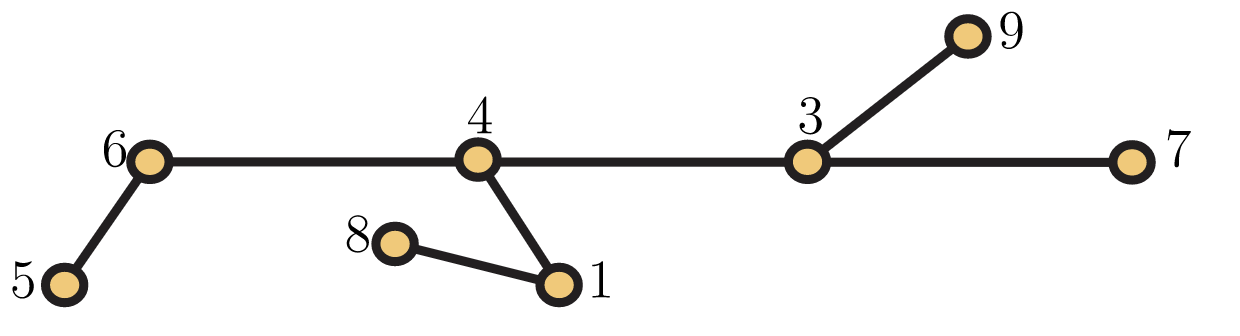
La llamada recursiva prüfer (\(T−v\)) devuelve (6, prüfer (\(T−v−v′\))), donde\(v′\) está el vértice etiquetado como 5. Continuando recursivamente, el siguiente vértice eliminado es 6, que añade un 4 a la cadena. Después se elimina 7, agregando 3. Siguiente 8 se elimina, anexando 1. A esto le sigue la supresión de 1, anexando 4. Finalmente se elimina 4, añadiendo 3, y la llamada recursiva final tiene el subárbol isomórfico a\(K_2\) con vértices etiquetados 3 y 9, y se devuelve una cadena vacía. Así, prüfer (\(T\)) = 6643143.
Ahora estamos preparados para dar una prueba de la Fórmula de Cayley.
- Prueba
-
Está claro que prüfer (T) toma un árbol etiquetado\(n\) -vértice con etiquetas de\([n]\) y devuelve una cadena de longitud\(n−2\) cuyos símbolos son elementos de\([n]\). Lo que aún tenemos que hacer es determinar una manera de tomar tal cadena y construir un árbol etiquetado\(n\) -vértice a partir de ella. Si podemos encontrar tal construcción, tendremos una biyección entre el conjunto\(T_n\) de árboles etiquetados en\(n\) vértices y el conjunto de cadenas de longitud de\(n−2\) cuyos símbolos provienen\([n]\), lo que implicará eso\(T_n = n^{n-2}\).
Primero, veamos cómo se comporta prüfer (T). ¿Qué números aparecen realmente en el código Prüfer? Los números que aparecen en el código de Prüfer son las etiquetas de los vértices no foliares de\(T\). La etiqueta de una hoja simplemente no puede aparecer, ya que siempre grabamos la etiqueta del vecino de la hoja que estamos borrando, y la única forma en que eliminaríamos al vecino de una hoja es si ese vecino también fuera una hoja, lo cual solo puede suceder\(T≅K_2\), en cuyo caso prüfer (T) simplemente devuelve la cadena vacía. Así, si\(I \subset [n]\) es el conjunto de símbolos que aparecen en prüfer (T), las etiquetas de las hojas de\(T\) son precisamente los elementos de\([n] - I\).
Con el conocimiento de qué etiquetas pertenecen a las hojas de\(T\) en la mano, estamos listos para usar la inducción para completar la prueba. Nuestro objetivo es mostrar que si se le da una cadena\(s=s_1s_2 \cdot \cdot \cdot s_{n−2}\) cuyos símbolos provienen de un conjunto\(S\) de\(n\) elementos, hay un árbol único\(T\) con prüfer (T) =\(s\). Si\(n=2\), la única cadena de este tipo es la cadena vacía, así que 1 y 2 ambas etiquetas se van y solo podemos construir\(K_2\). Ahora supongamos que tenemos el resultado para algunos\(m \geq 2\), y tratamos de demostrarlo para\(m+1\). Tenemos una cadena\(s=s_1s_2 \cdot \cdot \cdot s_{m−1}\) con símbolos de\([m+1]\). Dejar\(I\) ser el conjunto de símbolos que aparecen en\(s\) y dejar\(k\) ser el elemento menor de\([m+1]−I\). Por el párrafo anterior, sabemos que\(k\) es la etiqueta de una hoja de\(T\) y que su vecino único es el vértice etiquetado\(s_1\). La cadena\(s′=s_2s_3 \cdot \cdot \cdot s_{m−1}\) tiene longitud\(m−2\) y como\(k\) no aparece en\(s\), sus símbolos provienen de\(S=[m+1]−\{k\}\), que tiene tamaño\(m\). Así, por inducción, existe un árbol único\(T′\) cuyo código de Prüfer es\(s′\). Formamos\(T\) a partir de\(T′\) uniendo una hoja con etiqueta\(k\) al vértice de\(T′\) con etiqueta\(s_1\) y tenemos un árbol del tipo deseado.
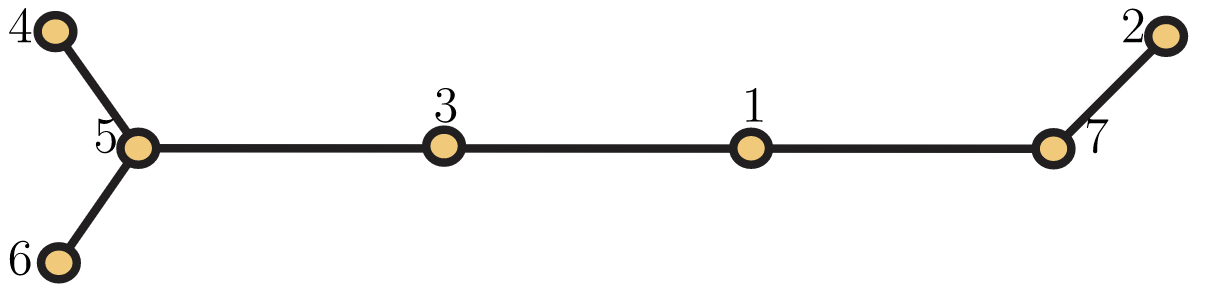
Cerramos esta sección con un ejemplo de cómo tomar un código de Prüfer y usarlo para construir un árbol etiquetado. Considera la cadena\(s=75531\) como un código Prüfer. Entonces el árbol\(T\) correspondiente a\(s\) tiene 7 vértices, y sus hojas están etiquetadas 2, 4 y 6. El paso inductivo en nuestra prueba une el vértice etiquetado 2 al vértice etiquetado 7 en el árbol\(T′\) con código Prüfer 5531 y etiquetas de vértice\(\{1,3,4,5,6,7\}\), ya que 2 se usa para etiquetar el último vértice agregado. ¿De qué son las hojas\(T′\)? Los símbolos en\(\{4,6,7\}\) no aparecen en 5531, por lo que deben ser las etiquetas de las hojas, y la construcción dice que adjuntaríamos el vértice etiquetado 4 al vértice etiquetado 5 en el árbol que obtenemos por inducción. En la Figura 5.44, mostramos cómo continúa este proceso recursivo.
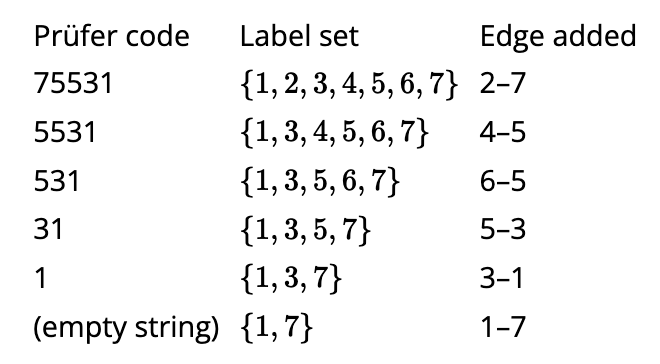
Formamos cada fila a partir de la fila de arriba eliminando la primera etiqueta utilizada en el borde agregado del conjunto de etiquetas y eliminando el primer símbolo del código de Prüfer. Una vez que el código de Prüfer se convierte en la cadena vacía, sabemos que las dos etiquetas restantes deben ser las etiquetas que colocamos en los extremos de\(K_2\) para comenzar a construir\(T\). Después trabajamos de nuevo hacia arriba la columna de borde agregado, agregando un nuevo vértice y el borde indicado. El árbol que construimos de esta manera se muestra en la Figura 5.45.