5.5: Gráficas Planares
- Page ID
- 118410
Volvamos al problema de proveer líneas de agua, luz y gas natural a tres viviendas que discutimos en la introducción a este capítulo. ¿Cómo podemos modelar este problema usando una gráfica? La mejor manera es tener un vértice para cada utilidad y un vértice para cada una de las tres viviendas. Entonces lo que estamos preguntando es si podemos dibujar la gráfica que tiene un borde de cada utilidad a cada hogar para que ninguno de los bordes se cruce. Esta gráfica se muestra en la Figura 5.29. Deberías reconocerla como la gráfica bipartita completa\(K_{3,3}\) que presentamos anteriormente en el capítulo.
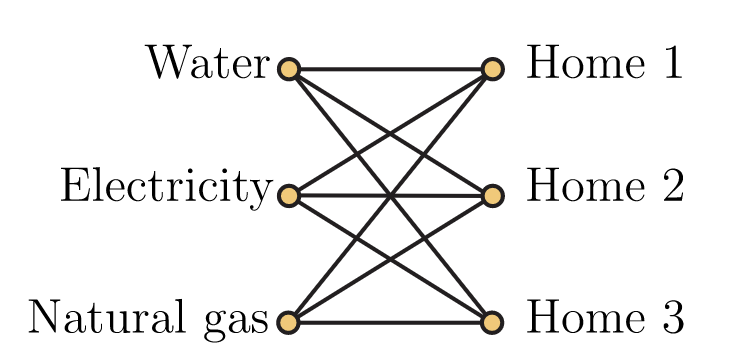
Si bien este ejemplo de líneas de servicios puede parecer un poco artificial, ya que realmente no hay una buena razón para que los proveedores no puedan enterrar sus líneas a diferentes profundidades, la cuestión de si se puede dibujar una gráfica en el plano de tal manera que los bordes se crucen solo en los vértices es una pregunta largamente estudiada en matemáticas que tiene aplicaciones útiles. Un área donde surge es en el diseño de microchips y placas de circuitos. En esos contextos, el material es tan delgado que la opción de colocar conexiones a diferentes profundidades o bien no existe o está severamente restringida. Hay muchas matemáticas profundas que subyace a esta área, y esta sección pretende introducir algunos de los conceptos clave.
Por un dibujo de una gráfica, nos referimos a una forma de asociar sus vértices con puntos en el plano cartesiano\(\mathbb{R}^2\) y sus aristas con simples arcos poligonales cuyos extremos son los puntos asociados a los vértices que son los extremos del borde. Se puede pensar en un arco poligonal como una secuencia finita de segmentos de línea de tal manera que el punto final de un segmento de línea es el punto de partida del siguiente segmento de línea, y un arco poligonal simple es aquel que no se cruza. (Nuestra elección de arcos poligonales en lugar de curvas arbitrarias en realidad no causa un impedimento, ya que al tomar segmentos de línea muy, muy, muy cortos podemos aproximar cualquier curva). Un dibujo plano de una gráfica es aquel en el que los arcos poligonales correspondientes a dos aristas se cruzan sólo en un punto correspondiente a un vértice al que ambos son incidentes. Un gráfico es plano si tiene un dibujo plano. Una cara de un dibujo plano de una gráfica es una región delimitada por aristas y vértices y que no contiene ningún otro vértice o arista.
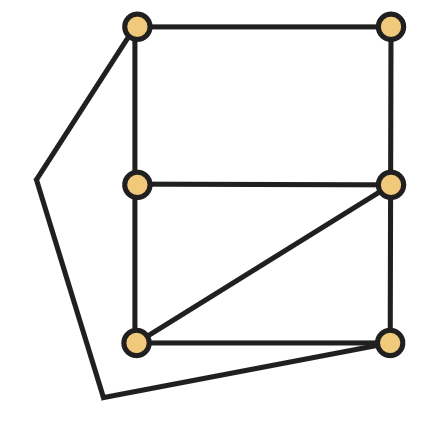
La Figura 5.30 muestra un dibujo plano de una gráfica con 6 vértices y 9 aristas. Observe cómo una de las aristas se dibuja como un verdadero arco poligonal en lugar de un segmento de línea recta. Este dibujo determina 5 regiones, ya que también contamos la región no delimitada que rodea al dibujo.
La Figura 5.31 muestra un dibujo plano de la gráfica completa\(K_4\). Hay 4 vértices, 6 aristas y 4 caras en el dibujo.
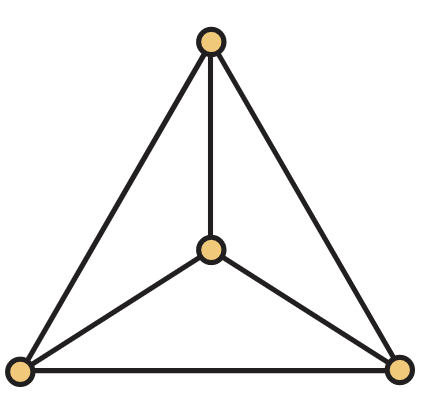
¿Qué sucede si calculamos el número de vértices menos el número de aristas más el número de caras para estos dibujos? Tenemos
\(6-9+5=2\)
\(4-6+4=2\)
Si bien puede parecer una coincidencia que este cálculo resulte en 2 para estos dibujos planos, aquí hay un principio más general en funcionamiento, y de hecho se mantiene para cualquier dibujo plano de cualquier gráfico plano.
De hecho, el número 2 aquí realmente resulta de una propiedad fundamental del plano, y hay unos teoremas correspondientes para otras superficies. No obstante, sólo necesitamos el resultado como se indicó anteriormente.
Dejar\(G\) ser una gráfica plana conectada con\(n\) vértices y\(m\) aristas. Cada dibujo plano de\(G\) tiene\(f\) caras, donde\(f\) satisface
\(n-m+f=2\)
- Prueba
-
Nuestra prueba es por inducción en el número\(m\) de bordes. Si\(m=0\), entonces ya que\(G\) está conectado, nuestra gráfica tiene un solo vértice, y así hay una cara. Así,\(n−m+f=1−0+1=2\) según sea necesario. Ahora supongamos que hemos probado la fórmula de Euler para todas las gráficas con menos de m bordes y dejar\(G\) tener\(m\) bordes. Elija un borde\(e\) de\(G\). ¿Qué pasa si formamos una nueva gráfica\(G′\) eliminando e de\(G\)? Si\(G′\) está conectado, se aplica nuestra hipótesis inductiva. Digamos que\(G′\) tiene\(n′\) vértices,\(m′\) aristas y\(f′\) caras. Luego, por inducción, estos números satisfacen
\(n' - m' + f' = 2\).
Ya que solo eliminamos un borde,\(n′=n\) y\(m′=m−1\). ¿Qué hizo la eliminación de\(e\) hacer al número de caras? En\(G′\) hay una nueva cara que antiguamente eran dos caras divididas por\(e\) en\(G\). Por lo tanto,\(f′=f−1\). Sustituyendo estos en\(n′−m′+f′=2\), tenemos
\(n-(m-1) + (f-1) = 2 \Longleftrightarrow n-m+f = 2\).
Así, si\(G′\) está conectado, ya terminamos. Si\(G′\) se desconecta, sin embargo, no podemos aplicar el supuesto inductivo a\(G′\) directamente. Afortunadamente, ya que eliminamos solo un borde,\(G′\) tiene dos componentes, los cuales podemos ver como dos gráficas conectadas\(G_1′\) y\(G_2′\). Cada uno de estos tiene menos de\(m\) bordes, por lo que podemos aplicarles la hipótesis inductiva. Para\(i=1,2\), deja\(n_i′\) ser el número de vértices\(G_i′, m_i′\) del número de aristas\(G_i′, and f_i′\) del número de caras de\(G_i′\). Entonces por inducción tenemos
\(n_1' - m_1' +f_1' = 2\)y\(n_2' - m_2' + f_2' = 2\).
Sumando estos juntos, tenemos
\((n_1' + n_2') - (m_1' + m_2') + (f_1' + f_2') = 4\).
Pero ahora\(n=n_1' + n_2'\) y\(m_1' + m_2' = m-1\), así la igualdad se convierte
\(n - (m-1) + (f_1' + f_2') = 4 \Longleftrightarrow n-m + (f_1' + f_2') = 3\).
Lo único que aún tenemos que averiguar es con qué\(f_1′+f_2′\) se relaciona\(f\), y tenemos que esperar que nos permita derribar el 3 a un 2. Cada cara de\(G_1′\) y\(G_2′\) es una cara de\(G\), ya que el hecho de que quitar\(e\) desconexiones\(G\) significa que\(e\) debe ser parte del límite de la cara no acotada. Además, la cara no acotada se cuenta dos veces en la suma\(f_1′+f_2′\), así\(f=f_1′+f_2′−1\). Esto da exactamente lo que necesitamos para completar la prueba.
Tomada por sí misma, la fórmula de Euler no parece tan útil, ya que requiere contar el número de caras en una incrustación plana. Sin embargo, podemos usar esta fórmula para obtener una forma rápida de determinar que una gráfica no es plana. Considera un dibujo sin cruces de borde de una gráfica sobre\(n\) vértices y m aristas, con\(n \geq 3\). Consideramos pares\((e,F)\) donde\(e\) es un borde de\(G\) y\(F\) es una cara que tiene\(e\) como parte de su límite. ¿Cuántos de esos pares hay? Llamemos al número de pares\(p\). Cada borde puede encuadernar una o dos caras, así que tenemos eso\(p \leq 2m\). También podemos encuadernar\(p\) contando el número de pares en los que\(F\) aparece una cara. Cada cara está delimitada por al menos 3 bordes, por lo que aparece en al menos 3 pares, y así\(p \geq 3f\). Así\(3f \leq 2m\) o\(f \leq 2m/3\). Ahora, utilizando la fórmula de Euler, tenemos
\(m=n+f - 2 \leq n + \frac{2m}{3} - 2 \Longleftrightarrow \frac{m}{3} \leq n-2\).
Así, hemos probado el siguiente teorema.
Un gráfico plano en\(n\) vértices tiene como máximo\(3n−6\) bordes cuando\(n \geq 3\).
El contrapositivo de este teorema, a saber, que una gráfica\(n\) -vértice con más de\(3n−6\) aristas no es plana, suele ser la formulación más útil de este resultado. Por ejemplo, hemos visto (Figura 5.31) que\(K_4\) es plano. ¿Y qué pasa\(K_5\)? Tiene 5 vértices y\(C(5,2)=10>9=3 \cdot 5−6\) aristas, por lo que no es plana, y por lo tanto para\(n \geq 5\), no\(K_n\) es plana, ya que contiene\(K_5\). Es importante tener en cuenta que el Teorema 5.33 no es el ser-todo, fin de determinar si una gráfica es plana. Para ver esto, volvamos al tema del dibujo\(K_{3,3}\) en el plano. Esta gráfica tiene 6 vértices y 9 aristas, por lo que pasa la prueba del Teorema 5.33. Sin embargo, si pasas un par de minutos tratando de encontrar una manera de dibujar\(K_{3,3}\) en el avión sin ningún borde cruzado, rápidamente comenzarás a creer que no se puede hacer, ¡y tendrías razón!
Para ver por qué no\(K_{3,3}\) es planar, tendremos que volver a la fórmula de Euler, y nuevamente trabajamos con pares borde-cara. Porque\(K_{3,3}\), vemos que cada arista tendría que ser parte del límite de dos caras, y las caras están delimitadas por ciclos. Además, dado que la gráfica es bipartita, no hay ciclos impares. Así, contando los pares borde-cara desde la perspectiva de borde, vemos que hay\(2m=18\) pares. Si dejamos\(f_k\) ser el número de caras delimitadas por un ciclo de longitud\(k\), entonces\(f=f_4+f_6\). Así, contando los pares borde-cara desde la perspectiva de la cara, hay\(4f_4+6f_6\) pares. De la fórmula de Euler, vemos que el número de caras\(f\) debe ser 5, así entonces\(4f_4+6f_6 \geq 20\). Pero a partir de nuestra cuenta de pares borde-cara, tenemos\(2m=4f_4+6f_6\), dando\(18 \geq 20\), lo cual es claramente absurdo. Por lo tanto, no\(K_{3,3}\) es plano.
En este punto, probablemente te estés preguntando “¿Y qué?” Hemos invertido una buena cantidad de esfuerzo para establecerlo\(K_5\) y no\(K_{3,3}\) somos planares. Claramente cualquier gráfica que las contenga también es no planar, pero hay muchas gráficas, así que podrías pensar que podríamos estar en esto para siempre. Afortunadamente, no lo seremos, ya que en su núcleo, la planaridad realmente se reduce a solo estas dos gráficas, como veremos pronto.
Si\(G=(V,E)\) es una gráfica y\(uv \in E\), entonces podemos formar una nueva gráfica\(G′\) llamada subdivisión elemental de\(G\) agregando un nuevo vértice\(v′\) y reemplazando el borde\(uv\) por bordes\(uv′\) y\(v′v\). En otras palabras,\(G′\) tiene conjunto de vértices\(V′=V \cup \{v′\}\) y conjunto de bordes\(E′=(E−\{uv\}) \cup \{uv′,v′v\}\). Dos gráficas\(G_1\) y\(G_2\) son homeomórficas si se pueden obtener de la misma gráfica por una secuencia (potencialmente trivial) de subdivisiones elementales.
El propósito de discutir las gráficas homeomórficas es que dos gráficas homeomórficas tengan las mismas propiedades a la hora de ser dibujadas en el plano. Para ver esto, piensa en lo que sucede\(K_5\) si formamos una subdivisión elemental de la misma a través de cualquiera de sus bordes. Claramente permanece no planar. De hecho, si tomas alguna gráfica no plana y formas la subdivisión elemental usando cualquiera de sus aristas, la gráfica resultante es no planar. El siguiente teorema muy profundo fue probado por el matemático polaco Kazimierz Kuratowski en 1930. Su prueba está más allá del alcance de este texto.
Una gráfica es plana si y sólo si no contiene una subgrafía homeomórfica a cualquiera\(K_5\) o\(K_{3,3}\).
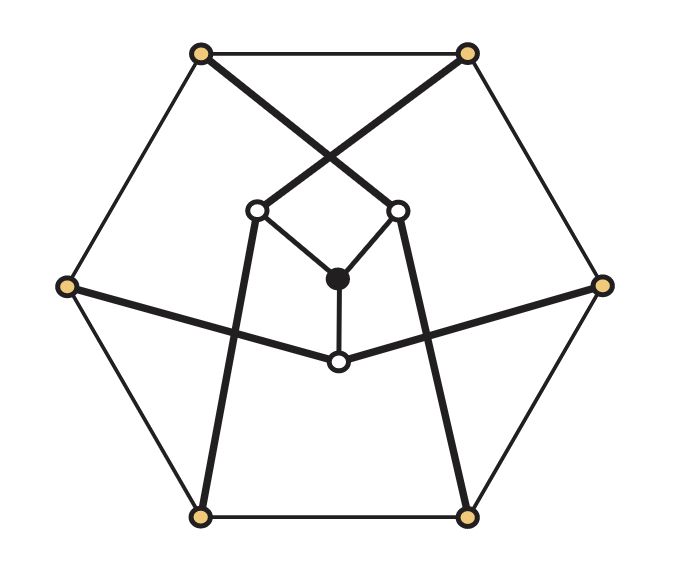
El teorema de Kuratowski da una manera útil de verificar si una gráfica es plana. Aunque no siempre es fácil encontrar un subgrafo homeomórfico a\(K_5\) o a\(K_{3,3}\) mano, existen algoritmos eficientes para pruebas de planaridad que hacen uso de esta caracterización. Para ver este teorema en funcionamiento, consideremos la gráfica de Petersen que se muestra en la Figura 5.17. El gráfico de Petersen tiene 10 vértices y 15 aristas, por lo que pasa la prueba del Teorema 5.33, y nuestro argumento usando la fórmula de Euler para demostrar que\(K_{3,3}\) es no planar fue lo suficientemente complejo, probablemente no queremos probarlo para la gráfica Petersen. Para usar el Teorema de Kuratowski aquí, tenemos que decidir si preferiríamos encontrar un subgrafo homeomórfico a\(K_5\) o a\(K_{3,3}\). Aunque la gráfica de Petersen se ve muy similar a\(K_5\), en realidad es simultáneamente demasiado similar y demasiado diferente para que podamos encontrar una subgrafía homeomórfica a\(K_5\), ya que cada vértice tiene grado 3. Así, nos propusimos encontrar una subgrafía de la gráfica Petersen homeomórfica a\(K_{3,3}\). Para ello, tenga en cuenta que\(K_{3,3}\) contiene un ciclo de longitud 6 y tres aristas que están en su lugar entre vértices opuestos entre sí en el ciclo. Identificamos un seis ciclos en la gráfica de Petersen y lo dibujamos como un hexágono y colocamos los cuatro vértices restantes dentro del ciclo. Dicho dibujo se muestra en la Figura 5.35. El subgrafo homeomórfico a\(K_{3,3}\) se encuentra eliminando el vértice negro, ya que entonces los vértices blancos tienen grado dos, y podemos reemplazar cada uno de ellos y sus dos bordes incidentes (mostrados en negrita) por un solo borde.
Cerramos esta sección con un problema que reúne a la sección actual con el tema de la coloración gráfica. En 1852 Francis Guthrie, un inglés que en ese momento estaba estudiando para ser abogado pero posteriormente se convirtió en profesor de matemáticas en Sudáfrica, estaba tratando de colorear un mapa de los condados de Inglaterra para que dos condados cualesquiera que compartieran un segmento límite (es decir, tocaron en más de un solo punto) fueran coloreado con diferentes colores. Se dio cuenta de que solo necesitaba cuatro colores para hacer esto, y no pudo dibujar ningún tipo de mapa que requiriera cinco colores. (Pudo encontrar un mapa que requirió cuatro colores, ejemplo de los cuales se muestra en la Figura 5.36.)
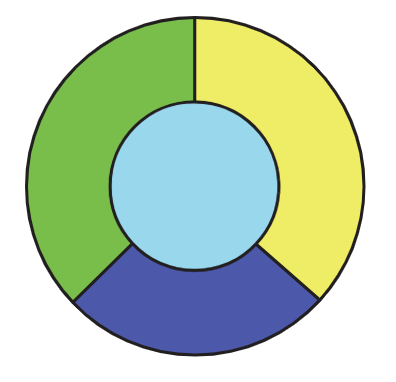
¿Podría ser cierto que cada mapa podría ser coloreado con solo cuatro colores? Preguntó a su hermano Frederick Guthrie, quien era estudiante de matemáticas en el University College de Londres, sobre el problema, y Frederick finalmente comunicó el problema a Augusto de Morgan (de la fama de las leyes de Morgan), uno de sus maestros. Fue de esta manera que nació uno de los problemas más famosos (o infames), conocido desde hace un siglo como el Problema de los Cuatro Colores y ahora el Teorema de los Cuatro Colores, en la teoría gráfica. De Morgan estaba muy interesado en el Problema de los Cuatro Colores, y se lo comunicó a Sir William Rowan Hamilton, destacado matemático irlandés y aquel por el que se nombran los ciclos hamiltonianos, pero Hamilton no encontró interesante el problema. Hamilton es una de las pocas personas que consideró el Problema de los Cuatro Colores pero que no quedó cautivado por él.
Continuaremos nuestra discusión sobre la historia del Teorema de los Cuatro Colores en un momento, pero primero, debemos considerar cómo podemos convertir el problema de colorear un mapa en una cuestión de teoría gráfica. Bueno, parece natural que a cada región se le asigne un vértice correspondiente. Queremos obligar a las regiones que comparten un límite a tener diferentes colores, por lo que esto sugiere que debemos colocar un borde entre dos vértices si y solo si sus regiones correspondientes tienen un límite común. (A modo de ejemplo, el mapa de la Figura 5.36 corresponde a la gráfica\(K_4\).) No es difícil ver que esto produce una gráfica plana, ya que podemos dibujar los bordes a través del segmento límite común. Además, con un poco de pensamiento, deberías ver que dado un dibujo plano de una gráfica, puedes crear un mapa en el que cada vértice conduce a una región y los bordes conducen a segmentos de límite comunes. Así, el Problema de los Cuatro Colores podría afirmarse como “¿Cada gráfica plana tiene un número cromático como máximo cuatro?”
El interés por el problema de los cuatro colores languideció hasta 1877, cuando el matemático británico Arthur Cayley escribió una carta a la Royal Society preguntando si el problema se había resuelto. Esto trajo el problema a la atención de muchas más personas, y la primera “prueba” del Teorema de los Cuatro Colores, debido a Alfred Bray Kempe, se completó en 1878 y se publicó un año después. Pasaron 11 años antes de que Percy John Heawood encontrara un defecto en la prueba pero pudo salvar lo suficiente como para mostrar que cada gráfica plana tiene un número cromático como máximo cinco. En 1880, Peter Guthrie Tait, físico británico mejor conocido por su libro Tratado de Filosofía Natural con Sir William Thomson (Lord Kelvin), hizo un anuncio que sugería que tenía una prueba del Teorema de los Cuatro Colores utilizando ciclos hamiltonianos en ciertas gráficas planas. Sin embargo, consistente con la forma en que Tait abordó algunas conjeturas en la teoría matemática de los nudos, parece que posteriormente se dio cuenta alrededor de 1883 que no podía probar que los ciclos hamiltonianos que estaba usando realmente existían y así Tait probablemente solo creía que tenía una prueba del Teorema de los Cuatro Colores por poco tiempo, si acaso. No obstante, tardaría hasta 1946 en encontrar un contraejemplo a la conjetura que Tait había utilizado en su intento de probar el Teorema de los Cuatro Colores.
En la primera mitad del siglo XX, se hicieron algunos avances incrementales hacia la resolución del Problema de los Cuatro Colores, pero pocos matemáticos destacados se interesaron seriamente en él. El empujón final para probar el Teorema de los Cuatro Colores vino con aproximadamente al mismo tiempo que las primeras computadoras electrónicas estaban entrando en uso generalizado en la industria y la investigación. En 1976, dos matemáticos de la Universidad de Illinois anunciaron su prueba asistida por computadora del Teorema de los Cuatro Colores. La prueba de Kenneth Appel y Wolfgang Haken llevó a la Universidad de Illinois a agregar la frase “CUATRO COLORES SUFICIENTES” a la huella de su medidor de franqueo.
Cada gráfica plana tiene un número cromático como máximo cuatro.
La prueba de Appel y Haken del Teorema de los Cuatro Colores fue como mínimo insatisfactoria para muchos matemáticos, y para algunos simplemente no era una prueba. Estos matemáticos sentían que el uso de una computadora para verificar varios casos era simplemente demasiado incierto; ¿cómo podría estar seguro de que el código que comprobaba las 1,482 “configuraciones inevitables” no contenía ningún error lógico? De hecho, se encontraron varios errores en los casos analizados, pero ninguno resultó ser fallas fatales. En 1989, Appel y Haken publicaron un tomo de 741 páginas titulado Every Planar Map is Four Colorable que proporcionó correcciones a todas las fallas conocidas en su argumento original. Esto todavía no satisfizo a muchos, y a principios de la década de 1990 un equipo formado por Neil Robertson de la Universidad Estatal de Ohio; Daniel P. Sanders, estudiante de posgrado en el Instituto Tecnológico de Georgia; Paul Seymour de Bellcore; y Robin Thomas de Georgia Tech anunciaron una nueva prueba del Teorema de los Cuatro Colores. No obstante, aún requería el uso de computadoras. La prueba sí obtuvo una aceptación más generalizada que la de Appel y Haken, en parte porque la nueva prueba utilizó menos de la mitad (633) del número de configuraciones que utilizó la prueba de Appel-Haken y el código de computadora se proporcionó en línea para que cualquiera lo verificara. Si bien sigue siendo insatisfactoria para muchos, la prueba de Robertson, et al. fue generalmente aceptada, y hoy en día el tema del Teorema de los Cuatro Colores se ha puesto fin en gran parte. No obstante, muchos todavía se preguntan si alguien encontrará alguna vez una prueba de esta sencilla afirmación que no requiere la asistencia de una computadora.


