6.1: Notación y Terminología Básicas
- Page ID
- 118419
Un conjunto o poset parcialmente ordenado\(P\) es un par\((X,P)\) donde\(X\) es un conjunto y\(P\) es una relación binaria reflexiva, antisimétrica y transitiva en\(X\). (Consulte la Sección B.10 para un repaso de lo que son estas propiedades si es necesario.) Llamamos\(X\) al conjunto de suelo mientras que\(P\) es un orden parcial encendido\(X\). Los elementos del conjunto\(X\) de suelo también se denominan puntos, y el poset\(P\) es finito si su conjunto de suelo\(X\) es un conjunto finito.
Vamos\(X=\{a,b,c,d,e,f\}\). Considere las siguientes relaciones binarias en\(X\).
\(R_1=\{(a,a),(b,b),(c,c),(d,d),(e,e),(f,f),(a,b),(a,c),(e,f)\}\)
\(R_2=\{(a,a),(b,b),(c,c),(d,d),(e,e),(f,f),(d,b),(d,e),(b,a),(e,a),(d,a),(c,f)\}\)
\(R_3=\{(a,a),(b,b),(c,c),(d,d),(e,e),(f,f),(a,c),(a,e),(a,f),(b,c),(b,d),(b,e),(b,f),(d,e),(d,f),(e,f)\}\)
\(R_4=\{(a,a),(b,b),(c,c),(d,d),(e,e),(f,f),(d,b),(b,a),(e,a),(c,f)\}\)
\(R_5=\{(a,a),(c,c),(d,d),(e,e),(a,e),(c,a),(c,e),(d,e)\}\)
\(R_6=\{(a,a),(b,b),(c,c),(d,d),(e,e),(f,f),(d,f),(b,e),(c,a),(e,b)\}\)
¿Cuáles de las relaciones binarias son órdenes parciales\(X\)? Para aquellos que no son órdenes parciales sobre\(X\), ¿qué bienes o propiedades se violan?
- Solución
-
Un poco de comprobación lo confirma\(R_1, R_2\) y\(R_3\) son órdenes parciales encendidas\(X\), así\(P_1=(X,R_1), P_2=(X,R_2)\) y\(P_3=(X,R_3)\) son posets. Varios de los otros ejemplos que discutiremos en este capítulo usarán el poset\(P_3=(X,R_3)\).
Por otro lado,\(R_4, R_5\) y no\(R_6\) son órdenes parciales sobre\(X\). Tenga en cuenta que no\(R_4\) es transitivo, ya que contiene (\(d,b\)) y (\(b,a\)) pero no\((d,a)\). La relación no\(R_5\) es reflexiva, ya que no contiene\((b,b)\). (Además, tampoco contiene\((f,f)\), pero una deficiencia es suficiente). Tenga en cuenta que\(R_5\) es una orden parcial en\(\{a,b,d,e\}\). La relación no\(R_6\) es antisimétrica, ya que contiene tanto\((b,e)\) y\((e,b)\).
Cuando\(P=(X,P)\) es un poset, es común escribir\(x \leq y\) en\(P\) o\(y \geq x\) en\(P\) como sustitutos de\((x,y) \in P\). Por supuesto, las notaciones\(x<y\) en\(P\) y\(y>x\) en\(P\) media\(x \leq y\) en\(P\) y\(x \neq y\). Cuando el poset\(P\) permanece fijo a lo largo de una discusión, a veces\(x \leq y\) abreviaremos con solo escribir\(x \leq y\), etc. Cuando\(x\) y\(y\) son puntos distintos de\(X\), decimos que\(x\) está cubierto por\(P\) \(y\)en\(P\) cuando\(x<y\) en\(P\), y no tiene sentido\(z \in X\) para cual\(x<z\) y\(z<y\) en\(P\). Por ejemplo, en el poset\(P_3=(X,R_3)\) del Ejemplo 6.3,\(d\) está cubierto por\(e\) y\(c\) cubre\(b\). Sin embargo, no\(a\) está cubierto por\(f\), ya que\(a<e<f\) en\(R_3\). Entonces podemos asociar con el poset\(P\) una gráfica de cubierta\(G\) cuyo conjunto de vértices es el conjunto\(X\) de suelo de\(P\) con\(xy\) un borde en\(G\) si y solo si uno de\(x\) y\(y\) cubre el otro en\(P\). Nuevamente, para el poset\(P_3\) del Ejemplo 6.3, mostramos la gráfica de portada en el lado izquierdo de la Figura 6.4. En realidad, en el lado derecho de esta figura sólo hay otro dibujo de esta misma gráfica.
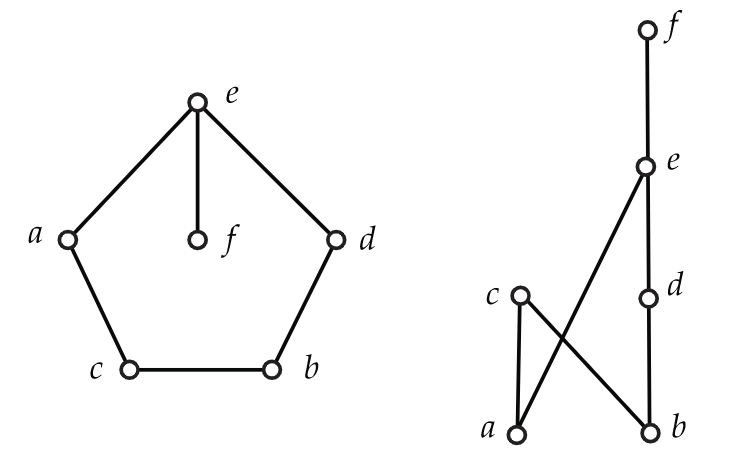
Es conveniente ilustrar un poset con un diagrama adecuadamente dibujado de la gráfica de cubierta en el plano euclidiano. Elegimos un sistema de coordenadas horizontal/vertical estándar en el plano y requerimos que la coordenada vertical del punto correspondiente\(y\) sea mayor que la coordenada vertical del punto correspondiente a\(x\) cada vez que\(y\) cubra\(x\) en\(P\). Cada borde en el gráfico de cubierta está representado por un segmento de línea recta que no contiene ningún punto correspondiente a ningún elemento del poset que no sea los asociados con sus dos puntos finales. Dichos diagramas se llaman diagramas Hasse (diagramas poset, diagramas de orden o simplemente diagramas). Ahora debería quedar claro que el dibujo del lado derecho de la Figura 6.4 es un diagrama del poset\(P_3\) del Ejemplo 6.3, mientras que el diagrama de la izquierda no lo es.
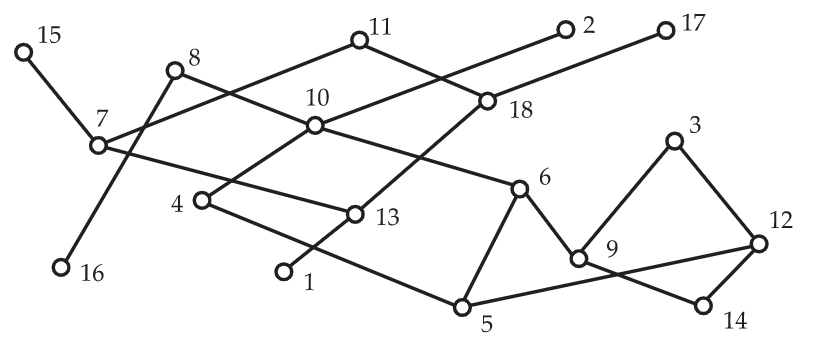
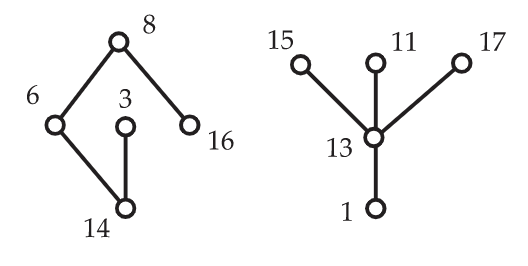
Para los posets de tamaño moderado, los diagramas se utilizan frecuentemente para definir un poset, en lugar de la notación de relación binaria explícita ilustrada en el Ejemplo 6.3. En la Figura 6.5, ilustramos un poset\(P=(X,P)\) con conjunto de tierra\(X=[17]=\{1,2,…,17\}\). Se necesitarían varias líneas de texto para escribir la relación binaria\(P\), y de alguna manera el diagrama sirve para darnos un sentido más táctil de las propiedades del poset.
Alice y Bob están hablando de cómo te comunicas con una computadora al trabajar con posets. Bob dice que las computadoras tienen capacidades gráficas increíbles en estos días y que solo le das a la computadora un escaneo pdf de un diagrama. Alice dice que duda de que alguien realmente haga eso. Carlos dice que hay varias estrategias efectivas. Una forma es etiquetar los puntos con enteros positivos desde\([n]\) donde\(n\) se encuentra el número de puntos en el conjunto de suelo y luego definir una\(n \times n\) matriz 0—1 A con entrada\(a(i,j)=1\) cuando\(i \leq j\) en\(P\) y de\(a(i,j)=0\) otra manera. Alternativamente, puede simplemente proporcionar para cada elemento\(i\) en el conjunto de suelo un vector que\(U(x)\) enumera todos los elementos que son mayores que\(x\) en\(P\). Este vector puede ser lo que los informáticos llaman una lista enlazada.
Un orden parcial\(P\) se denomina orden total (también, un orden lineal) si para todos\(x,y \in X\), ya sea\(x \leq y\) en\(P\) o\(y \leq x\) en\(P\). Para conjuntos finitos pequeños, podemos especificar un orden lineal enumerando los elementos de menor a mayor. Por ejemplo,\(L=[b,c,d,a,f,g,e]\) es el orden lineal en el suelo establecido\(\{a,b,c,d,e,f,g\}\) con\(b<c<d<a<f<g<e\) in\(L\).
El conjunto de números reales viene equipado con un orden total natural. Por ejemplo,\(1<7/5<\sqrt{2}< \pi \) en este orden. Pero en este capítulo, nos interesará primordialmente con órdenes parciales que no sean órdenes lineales. También, observamos que se debe tener especial cuidado a la hora de discutir órdenes parciales en conjuntos terrestres cuyos elementos son números reales. Para el poset mostrado en la Figura 6.5, tenga en cuenta que 14 es menor que 8, mientras que 3 y 6 son incomparables. Mejor no decirle a tus padres que has aprendido que bajo ciertas circunstancias, 14 puede ser menor que 8 y que tal vez puedas decir cuál de 3 y 6 es más grande que el otro. La sutileza puede perderse en la acalorada discusión que seguramente seguirá.
Hay varias formas bastante naturales de construir posets.
- Una familia\(\mathcal{F}\) de conjuntos está parcialmente ordenada por inclusión, es decir, establecer\(A \leq B\) si y solo si\(A\) es un subconjunto de\(B\).
- Un conjunto\(X\) de enteros positivos está parcialmente ordenado por división, sin resto, es decir, establece\(m \leq n\) if y solo if\(n \equiv 0\) (mod\(m\)).
- Un conjunto\(X\) de\(t\) -tuplas de números reales está parcialmente ordenado por la regla
\((a_1,a_2,…,a_t) \leq (b_1,b_2,…,b_t)\)
si y sólo si\(a_i \leq b_i\) en el orden natural encendido\(\mathcal{R}\) para\(i = 1,2,...,t\).
- Cuando\(L_1, L_2,…,L_k\) son órdenes lineales en el mismo conjunto\(X\), podemos definir un orden parcial\(P\) encendido\(X\) estableciendo\(x \leq y\) en\(P\) si y solo si\(x \leq y\) en\(L_i\) para todos\(i=1,2,…,k\).
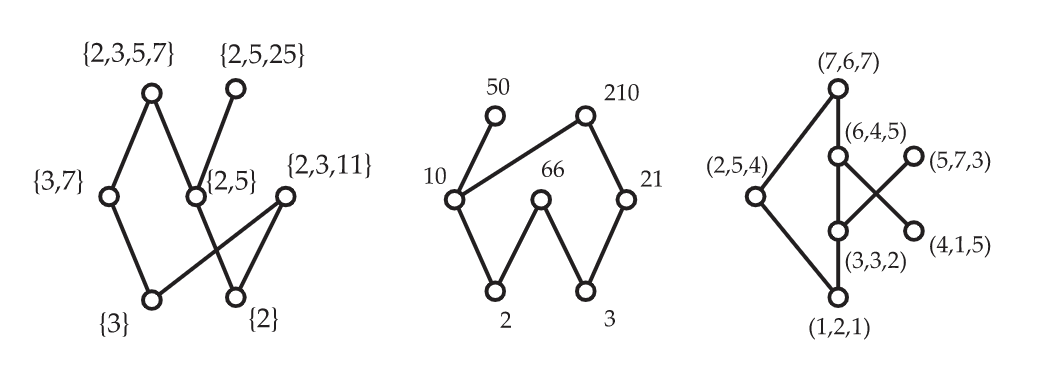
Ilustramos las tres primeras construcciones con los posets mostrados en la Figura 6.8. Como ahora está claro, en la discusión al comienzo mismo de este capítulo, Dave dibujó un diagrama para el poset determinado por la intersección de los órdenes lineales dados por Alice y el crítico de cine.
Los puntos distintos\(x\) y\(y\) en un poset\(P=(X,P)\) son comparables si ya sea\(x<y\) en\(P\) o\(x>y\) en\(P\); de otro modo\(x\) y\(y\) son incomparables. Si\(x\) y\(y\) son incomparables en\(P\), a veces escribimos\(x‖y\)\(P\) en.Con un poset\(P=(X,P)\), asociamos una gráfica de comparabilidad\(G_1=(X,E_1)\) y una gráfica de incomparabilidad \(G_2=(X,E_2)\). Los bordes en la gráfica de comparabilidad\(G_1\) consisten en los pares comparables y los bordes en la gráfica de incomparabilidad son los pares incomparables. Ilustramos estas definiciones en la Figura 6.9 donde mostramos la gráfica de comparabilidad y la gráfica de incomparabilidad del poset\(P_3\).
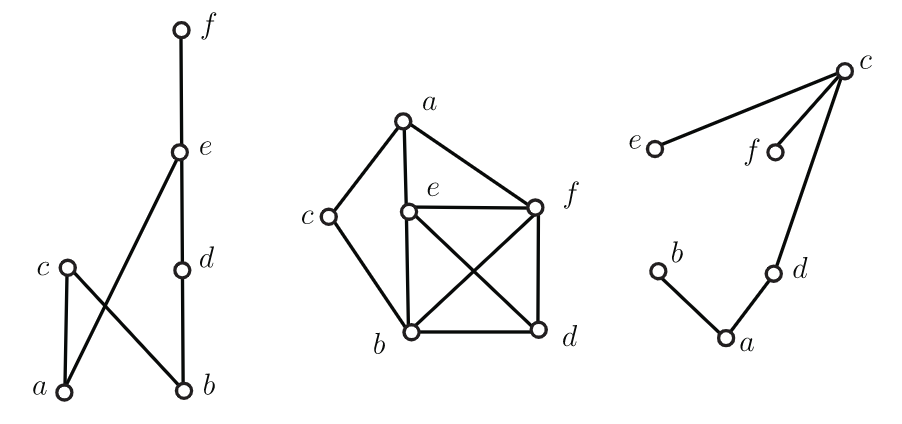
Cuando\(P=(X,P)\) es un poset y\(Y \subseteq X\), la relación binaria\(Q=P \bigcap (Y \times Y)\) es un orden parcial encendido\(Y\), y llamamos al poset\((Y,Q)\) un subposet de\(P\). En la Figura 6.10, se muestra una citación del poset presentado primero en la Figura 6.5.
Cuando\(P=(X,P)\) es un poset y\(C\) es un subconjunto de\(X\), decimos que\(C\) es una cadena si cada par distinto de puntos de\(C\) es comparable en\(P\). Cuando\(P\) es un orden lineal, todo el conjunto de tierra\(X\) es una cadena. Dualmente, si\(A\) es un subconjunto de\(X\), decimos que\(A\) es una anticadena si cada par distinto de puntos de\(A\) es incomparable en\(P\). Tenga en cuenta que un subconjunto de un elemento es tanto una cadena como una anticadena. Además, consideramos el conjunto vacío como una cadena y una anticadena.
La altura de un poset\(P=(X,P)\), denotada altura (P), es la mayor\(h\) para la que existe una cadena de\(h\) puntos en\(P\). Dualmente, el ancho de un poset\(P=(X,P)\), denotado ancho (P), es el más grande\(w\) para el que existe una anticadena de\(w\) puntos en\(P\).
Dado un poset\(P=(X,P)\), ¿qué tan difícil es determinar su altura y anchura? Bob dice que es muy fácil. Por ejemplo, para encontrar el ancho de un poset, simplemente enumere todos los subconjuntos de\(X\). Eliminar aquellos que no sean anticadena. La respuesta es el tamaño del subconjunto más grande que queda. Es rápido en afirmar que con el mismo enfoque se trabajará para encontrar la altura. Alice gime ante la ingenuidad de Bob y sugiere que debería leer más en este capítulo.


