6.2: Conceptos adicionales para Posets
- Page ID
- 118430
Decimos\((X,P)\) y\((Y,Q)\) somos isomórficos, y escribimos\((X,P)≅(Y,Q)\) si existe una biyección (1—1 y en mapa)\(f:X \rightarrow Y\) para que\(x_1 \leq x_2\) en\(P\) si y solo si\(f(x_1) \leq f(x_2)\) en\(Q\). En esta definición, el mapa\(f\) se llama isomorfismo de\(P\) a\(Q\). En la Figura 6.8, los dos primeros posets son isomórficos.
Bob ve un patrón que une los dos primeros posets mostrados en la Figura 6.8 y afirma que cualquier poset de uno de estos dos tipos es isomórfico a un poset del otro tipo. Alice admite que Bob tiene razón, pero aún más es cierto. Las cuatro construcciones dadas en el Ejemplo 6.7 son universales en el sentido de que cada poset es isomórfico a un poset de cada uno de los cuatro tipos. ¿Ves por qué? Si te quedas atascado respondiendo esto, revisaremos la pregunta al final del capítulo, y te daremos una pista.
Un isomorfismo de\(P\) a\(P\) se llama automorfismo de\(P\). Un isomorfismo de\(P\) a una citación de\(Q\) se llama incrustación de\(P\) en\(Q\). En la mayoría de los escenarios, no vamos a distinguir entre posets isomórficos, y diremos que un poset\(P=(X,P)\) está contenido en\(Q=(Y,Q)\) (también Q contiene P) cuando hay una incrustación de\(P\) in\(Q\). También, diremos que\(P\) excluye\(Q\) cuando ningún citación de\(P\) es isomórfico a\(Q\), y con frecuencia diremos\(P=Q\) cuándo\(P\) y\(Q\) son isomórficos.
Con la noción de isomorfismo, somos conducidos naturalmente a la noción de un poset “no etiquetado”, y en la Figura 6.13, mostramos un diagrama para tal poset.
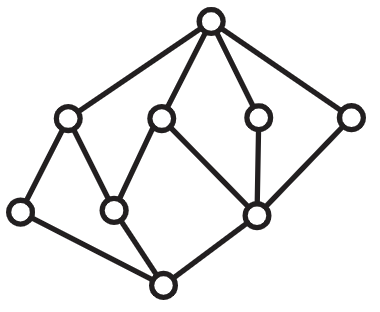
¿Qué tan difícil es saber si dos posets son isomórficos? Bob piensa que no es demasiado difícil. Bob dice que si le das una bijección entre los conjuntos de tierra, entonces puede determinar rápidamente si has establecido que los dos posets son isomórficos. Alice siente que Bob está confundiendo el tema de probar si dos posets son isomórficos con simplemente verificar que una bijección en particular puede ser certificada como un isomorfismo. El primer problema le parece mucho más difícil. Carlos dice que piensa que en realidad es muy difícil y que de hecho, nadie sabe si hay un buen algoritmo.
Obsérvese que el poset mostrado en la Figura 6.13 tiene la propiedad de que solo hay un punto máximo. Tal punto a veces se le llama uno, denotado no en vano como 1. Además, solo hay un punto mínimo, y se le llama cero, denotado 0.
El dual de un orden parcial\(P\) en un conjunto\ X\) se denota por\(P^d\) y se define por\(P^d=\{(y,x):(x,y) \in P\}\). El dual de un poset\(P=(X,P)\) se denota por\(P^d\) y se define por\(P^d=(X,P^d)\). Un poset\(P\) es auto-dual si\(P=P^d\).
Un poset\(P=(X,P)\) está conectado si su gráfica de comparabilidad está conectada, es decir, para cada\(x,y \in X\) con\(x \neq y\), hay una secuencia finita\(x=x_0,x_1,…,x_n=y\) de puntos de\(X\) manera que\(x_i\) es comparable a\(x_{i+1}\) in\(P\) for\(i=0,1,2,…,n−1\). Un subposet\((Y,P(Y))\) of\((X,P)\) se llama un componente de\(P\) if\((Y,P(Y))\) está conectado y no hay ningún subconjunto\(Z \subseteq X\) que contenga\(Y\) como un subconjunto apropiado para el cual\((Z,P(Z))\) está conectado. Un componente de un punto es trivial (también, un punto flojo o punto aislado); los componentes de dos o más puntos no son triviales. Tenga en cuenta que un punto suelto es tanto un elemento mínimo como un elemento máximo. Volviendo al poset mostrado en la Figura 6.5, vemos que tiene dos componentes.
Es natural decir que una gráfica\(G\) es una gráfica de comparabilidad cuando hay un poset\(P=(X,P)\) cuya gráfica de comparabilidad es isomórfica a\(G\). Por ejemplo, mostramos en la Figura 6.15 una gráfica sobre 6 vértices que no es una gráfica de comparabilidad. (Dejamos como ejercicio la tarea de establecer esta reclamación.)
De igual manera, decimos que una gráfica\(G\) es una gráfica de portada cuando existe un poset\(P=(X,P)\) cuya gráfica de portada es isomórfica a\(G\). No todas las gráficas son una gráfica de portada. En particular, cualquier gráfica que contenga un triángulo no es una gráfica de portada. En los ejercicios al final del capítulo, se le pedirá que construya gráficos sin triángulos que no sean gráficos de cobertura, con algunas pistas sobre cómo proceder.
Bob está bastante tomado con gráficas asociadas a posets. Hace las siguientes afirmaciones.
- Sólo los órdenes lineales tienen trazados como gráficos de cubierta.
- Un poset y su dual tienen la misma gráfica de portada y la misma gráfica de comparabilidad.
- Dos posets cualesquiera con la misma gráfica de portada tienen la misma altura y el mismo ancho.
- Dos posets cualesquiera con la misma gráfica de comparabilidad tienen la misma altura y el mismo ancho.
Alice se encoge de hombros y dice que Bob tiene razón la mitad del tiempo. ¿Cuáles dos aseveraciones son correctas?
Sin inmutarse, Bob señala que la gráfica de comparabilidad que se muestra en la Figura 6.9 es también una gráfica de incomparabilidad (para otro poset). Continúa postulando que esto siempre es cierto, es decir, siempre\(G\) que sea la gráfica de comparabilidad de un poset\(P\), hay otro poset\(Q\) para el cual\(G\) es la gráfica de incomparabilidad de\(Q\). Alice dice que Bob tiene razón en el primer recuento pero no está tan segura del segundo. Dave murmura que deberían echar un vistazo a la gráfica de comparabilidad del tercer poset en la Figura 6.8. Esta gráfica no es una gráfica de incomparabilidad. Pero en su típica manera confusa, Dave no ofrece ninguna justificación para esta afirmación. ¿Puedes ayudar a Alice y Bob a ver por qué Dave tiene razón?
Bob está en rollo y continúa sugiriendo que es relativamente fácil determinar si una gráfica es una gráfica de comparabilidad (la leyó en la web), pero tiene la sensación de que determinar si una gráfica es una gráfica de portada podría ser difícil. ¿Crees que tiene razón, en cualquiera de los dos casos?


