6.3: Teorema de la cobertura de cadenas de Dilworth y su doble

En esta sección, probamos el siguiente teorema de R.P. Dilworth, que es verdaderamente uno de los resultados clásicos de las matemáticas combinatorias.

Teorema 6.17. Teorema de Dilworth

Si\(P=(X,P)\) es un poset y ancho\((P)=w\), entonces existe una partición\(X=C_1 \cup C_2 \cup \cdot \cdot \cdot \cup C_w\), donde\(C_i\) es una cadena para\(i=1,2,…,w\). Además, no hay división de cadena en menos cadenas.

Antes de continuar con la prueba del teorema de Dilworth en la Subsección 6.3.1, hacemos una pausa para discutir la versión dual para particiones en anticadenas, ya que es aún más fácil de probar.

Teorema 6.18. Doble del teorema de Dilworth

Si\(P=(X,P)\) es un poset y una altura\(⁡(P)=h\), entonces existe una partición\(X=A_1 \cup A_2 \cup \cdot \cdot \cdot \cup A_h\), donde\(A_i\) es un anticadena para\(i=1,2,…,h\). Además, no hay partición usando menos anticadena.

Prueba

Para cada uno\(x \in X\), deja\(height⁡(x)\) ser el entero más grande\(t\) para el que existe una cadena

\(x_1 < x_2 < \cdot \cdot \cdot < x_t\)

con\(x=x_t\). Evidentemente,\(height⁡(x) \geq h\) para todos\(x \in X\). Entonces para cada\(i=1,2,…,h\) let\(A_i=\{x \in X:height⁡(x)=i\}\). Es fácil ver que cada uno\(A_i\) es un anticadena, como si\(x,y \in A_i\) fueran tales que\(x<y\), entonces hay una cadena\(x_1<x_2< \cdot \cdot \cdot <x_i=x<x_{i+i}=y\), entonces\(height⁡(y) \geq i+1\). Ya que\(height⁡(P)=h\), hay una cadena máxima\(C=\{x_1,x_2,…,x_h\}\). Si fuera posible\(P\) dividir en\(t<h\) anticadena, entonces por el Principio de Agujero Paloma, una de las anticadena contendría dos puntos de\(C\), pero esto no es posible.

Cuando\(P=(X,P)\) es un poset, un punto\(x \in X\) con\(height⁡(x)=1\) se llama punto mínimo de\(P\). Denotamos el conjunto de todos los puntos mínimos de un poset\(P=(X,P)\) por\(min(X,P)\).

El argumento dado para la prueba del Teorema 6.18 arroja un algoritmo eficiente, uno que se define recursivamente. Set\(P_0=P\). Si se\(P_i\) ha definido y\(P_i \neq \emptyset\), let\(A_i=min(P_i)\) y luego let\(P_{i+1}\) denotan el citatorio restante cuando\(A_i\) se elimina de\(P_i\).

En la Figura 6.19, se ilustra la partición anticadena proporcionada por este algoritmo para el poset de 17 puntos de la Figura 6.5. Los puntos oscurecidos forman una cadena de tamaño 5.

Figura 6.19. Un Poset de Altura 5

Discusión 6.20.

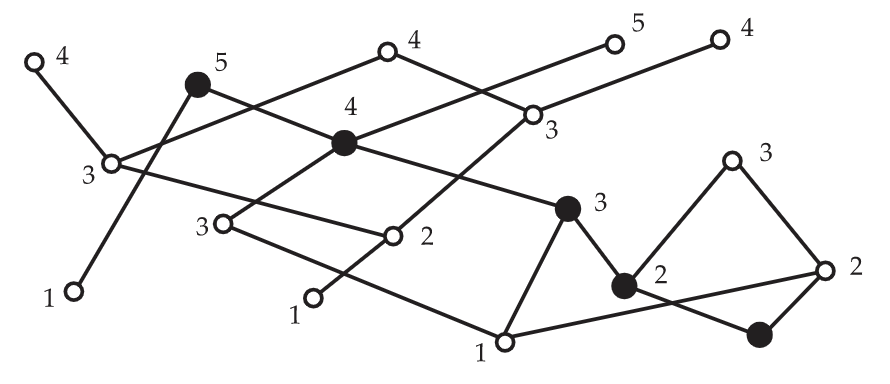
Alice afirma que es muy fácil encontrar el conjunto de elementos mínimos de un poset. ¿Estás de acuerdo?

Dualmente, podemos hablar del conjunto max (P) de puntos máximos de P. También podemos dividir P en anticadena de altura (P) eliminando recursivamente el conjunto de puntos máximos.

Hacemos una pausa para comentar que cuando\(P=(X,P)\) es un poset, el conjunto de todas las cadenas de\(P\) está en sí mismo parcialmente ordenado por inclusión. Por lo que es natural decir que una cadena\(C\) es máxima cuando no hay cadena\(C′\) que contenga\(C\) como subconjunto propio. Además, una cadena\(C\) es máxima cuando no hay cadena\(C′\) con\(|C|<|C′|\). Por supuesto, una cadena máxima es máxima, pero las cadenas máximas no necesitan ser máximas.

Las anticadenas máximas y las anticadenas máximas se definen análogamente.

Con esta terminología, el empuje del Teorema 6.18 es que es fácil encontrar la altura\(h\) de un poset así como una cadena máxima\(C\) que consiste en h puntos de\(P\). Por supuesto, también obtenemos una partición práctica del poset en\(h\) anticadena.

6.3.1 Prueba del teorema de Dilworth

El argumento para el teorema de Dilworth se simplifica con la siguiente notación. Cuando\(P=(X,P)\) es un poset y\(x \in X\), dejamos entrar\(D(x)=\{y \in X:y<x in P\}\)\(D[x]=\{y \in X:y \leq x in P\}\); entrar\(U(x)=\{y \in X:y>x in P\}\);\(U[x]=\{y \in X:y \geq x\}\); y entrar\(I(x)=\{y \in X−\{x\}:x‖y in P\}\). Cuando\(S \subseteq X\), dejamos\(D(S)=\{y \in X:y<x\) entrar\(P\), para algunos\(x \in S\}\) y\(D[S]=S \cup D(S)\). Los subconjuntos\(U(S)\) y\(U[S]\) se definen dualmente. Llamamos\(D(x), D[x], D(S)\), y\(D[S]\) bajamos sets, mientras\(U(x), U[x], U(S)\), y\(U[S]\) son conjuntos levantados. Tenga en cuenta que cuando\(A\) es una anticadena máxima en\(P\), el conjunto de tierra se\(X\) puede dividir en conjuntos disjuntos por pares como\(X=A \cup D(A) \cup U(A)\).

Ya estamos listos para la prueba. Dejar\(P=(X,P)\) ser un poset y dejar\(w\) denotar el ancho de\(P\). Al igual que en el Teorema 6.18, el Principio de Agujero Paloma implica que requerimos al menos\(w\) cadenas en cualquier partición de cadena de\(P\). Para probar eso\(w\) suficiente, procedemos por inducción sobre\(|X|\), siendo el resultado trivial si\(|X|=1\). Asumir validez para todos los posets con\(|X| \leq k\) y supongamos que\(P=(X,P)\) es un poset con\(|X|=k+1\). Sin pérdida de generalidad,\(w>1\); de lo contrario, la partición trivial\(X=C_1\) satisface la conclusión del teorema. Además, observamos que si\(C\) es una cadena (no vacía) en\((X,P)\), entonces podemos suponer que el subposet\((X−C,P(X−C))\) también tiene ancho\(w\). Para ver esto, observaremos que el teorema se mantiene para el citatorio, de manera que si\(width⁡(X−C,P(X−C))=w′<w\), entonces podemos particionarlo\(X−C\) como\(X−C=C_1 \cup C_2 \cup \cdot \cdot \cdot \cup C_{w′}\), así que eso\(X=C \cup C_1 \cup \cdot \cdot \cdot \cup C_{w′}\) es una partición en\(w′+1\) cadenas. Ya que\(w′<w\), sabemos\(w′+1 \leq w\), entonces tenemos una partición de\(X\) en a lo sumo\(w\) cadenas. Dado que cualquier partición de\(X\) en cadenas debe usar al menos\(w\) cadenas, esta es exactamente la partición que buscamos.

Elija un punto máximo\(x\) y un punto mínimo\(y\) con\(y \leq x\) in\(P\). Entonces deja\(C\) ser la cadena que contiene sólo los puntos\(x\) y\(y\). Tenga en cuenta que\(C\) contiene uno o dos elementos dependiendo de si\(x\) y\(y\) son distintos.

Dejar\(Y=X−C\)\(Q=P(Y)\) y dejar\(A\) ser un\(w\) elemento anticadena -elemento en el citatorio\((Y,Q)\). En la partición\(X=A \cup D(A) \cup U(A)\), el hecho de que\(y\) sea un punto mínimo mientras que\(A\) sea una anticadena máxima implica que\(y \in D(A)\). De igual manera,\(x \in U(A)\). En particular, esto demuestra que\(x\) y\(y\) son distintos.

Etiquetar los elementos de\(A\) as\(\{a_1,a_2,…,a_w\}\). Tenga en cuenta que\(U[A] \neq X\) desde\(y \notin U[A]\), y\(D[A] \neq X\) desde entonces\(x \notin D[A]\). Por lo tanto, podemos aplicar la hipótesis inductiva a los citatorios de\(P\) determinados por\(D[A]\) y\(U[A]\), respectivamente, y dividir cada uno de estos dos subconjuntos en\(w\) cadenas:

\(U[A] = C_1 \cup C_2 \cup \cdot \cdot \cdot \cup C_w\)y\(D[A] = D_1 \cup D_2 \cup \cdot \cdot \cdot \cup D_w\).

Sin pérdida de generalidad, podemos suponer que estas cadenas han sido etiquetadas de manera que\(a_i \in C_i ∩ D_i\) para cada una\(i=1,2,…,w\). Sin embargo, esto implica que

\(X=(C_1 \cup D_1) \cup (C_2 \cup D_2) \cup \cdot \cdot \cdot \cup (C_w \cup D_w)\)

es la partición deseada que a su vez completa la prueba.

En la Figura 6.21, ilustramos el teorema de cobertura de cadenas de Dilworth para el poset introducido por primera vez en la Figura 6.5. Los puntos oscurecidos forman una anticadena de 7 elementos, mientras que las etiquetas proporcionan una partición en 7 cadenas.

Figura 6.21. Un Poset de Ancho 7

Discusión 6.22.

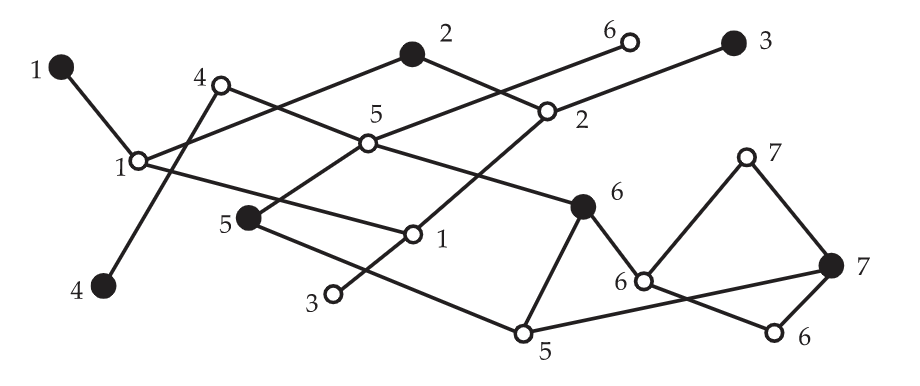
La siempre alerta Alice señala que la prueba dada anteriormente para el teorema de Dilworth no parece proporcionar un algoritmo eficiente para encontrar el ancho\(w\) de un poset, mucho menos una partición del poset en\(w\) cadenas. Bob aún no ha averiguado por qué enumerar todos los subconjuntos de\(X\) es una mala idea. Carlos está sentado en silencio escuchando sus riñas, pero finalmente, dice que un programador hábil puede idear un algoritmo a partir de la prueba. Se anima a los estudiantes a discutir este dilema, pero tenga la seguridad de que volveremos a este tema más adelante en el texto.