6.5: La celosía del subconjunto

Cuando\(X\) es un conjunto finito, la familia de todos los subconjuntos de\(X\), parcialmente ordenados por inclusión, forma un retículo de subconjunto . Esto lo ilustramos en la Figura 6.26 donde mostramos la celosía de todos los subconjuntos de {1,2,3,4}. En esta figura, tenga en cuenta que estamos representando conjuntos por cadenas de bits, y hemos abreviado aún más la notación escribiendo cadenas sin comas y paréntesis.

Figura 6.26. Una celosía de subconjunto

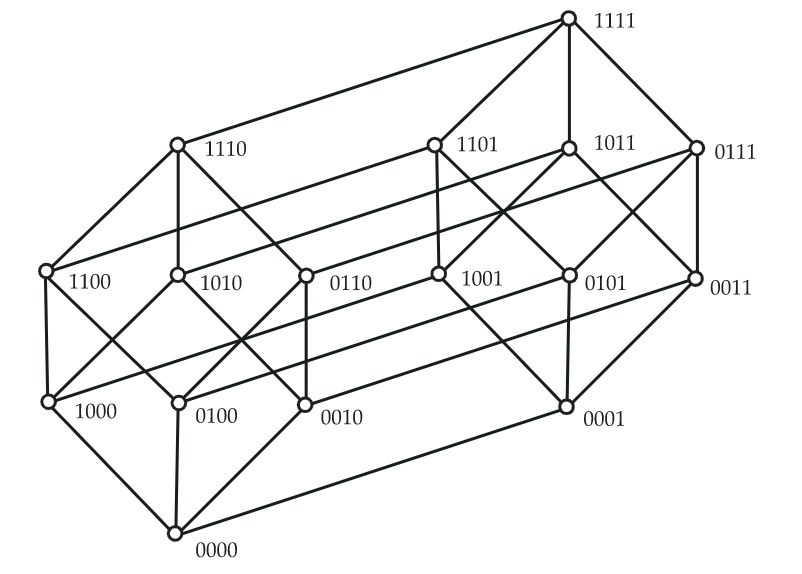
Para un entero positivo\(t\), dejamos\(2^t\) denotar el retículo subconjunto que consiste en todos los subconjuntos de\(\{1,2,…,t\}\) ordenados por inclusión. Algunas propiedades elementales de este poset son:

1. La altura es\(t+1\) y todas las cadenas máximas tienen exactamente\(t+1\) puntos.
2. El tamaño del poset\(\textbf{2}^t\) es\(2^t\) y los elementos se particionan en rangos (anticadena)\(A_0,A_1,…,A_t\) con\(|A_i|= \binom{t}{i}\) para cada uno\(i=0,1,…,t\).
3. El tamaño máximo de un rango en la red del subconjunto ocurre en el medio, es decir, si\(s=⌊t/2⌋\), entonces el coeficiente binomial más grande en la secuencia\( \binom{t}{0}, \binom{t}{1}, \binom{t}{2},…,\binom{t}{t}\) es\( \binom{t}{s}\). Tenga en cuenta que cuando\(t\) es impar, hay dos rangos de tamaño máximo, pero cuando\(t\) es par, solo hay uno.

6.5.1 Teorema de Sperner

Para el ancho de la celosía del subconjunto, tenemos el siguiente resultado clásico de Sperner.

Teorema 6.27. Teorema de Sperner

Para cada uno\(t \geq 1\), el ancho de la red del subconjunto\(2^t\) es el tamaño máximo de un rango, es decir,

ancho\((\textbf{2}^t) = \dbinom{t}{⌊\frac{t}{2}⌋}\)

Prueba

El ancho del poset\(\textbf{2}^t\) es al menos\(C(t,\frac{t}{2}⌋)\) ya que el conjunto de todos los subconjuntos\(⌊\frac{t}{2}⌋\) -elementos de\(\{1,2,…,t\}\) es un anticadena. Ahora mostramos que el ancho de\(\textbf{2}^t\) es como máximo\(C(t,⌊\frac{t}{2}⌋)\).

Dejar\(w\) ser el ancho de\(\textbf{2}^t\) y dejar\(\{S_1,S_2,…,S_w\}\) ser una anticadena de tamaño\(w\) en este poset, es decir, cada uno\(S_i\) es un subconjunto de\(\{1,2,…,t\}\) y si\(1 \leq i<j \leq w\), entonces\(S_i \nsubseteq S_j\) y\(S_j \nsubseteq S_i\).

Para cada uno\(i\), considere el conjunto\(S_i\) de todas las cadenas máximas que atraviesan\(S_i\). Es fácil ver que si\(|S_i|=k_i\), entonces\(|S_i|=k_i!(t−k_i)!\). Esto se desprende de la observación de que para formar dicha cadena máxima comenzando con\(S_i\) como punto intermedio, se eliminan los elementos de\(S_i\) uno a la vez para formar los conjuntos de la parte inferior de la cadena. También, para formar la parte superior de la cadena, se agregan los elementos no de\(S_i\) uno a la vez.

Obsérvese además que si\(1 \leq i<j \leq w\)\(S_i \cap S_j= \emptyset\), entonces, porque si hubiera una cadena máxima perteneciente a ambos\(S_i\) y\(S_j\), entonces implicaría que uno de Si y Sj es un subconjunto de la otra.

En total, hay exactamente cadenas\(t!\) máximas en\(\textbf{2}^t\). Esto implica que

\(\displaystyle \sum_{i=1}^w k_i!(t-k_i)! \leq t!\).

Esto implica que

\( \displaystyle \sum_{i=1}^w \dfrac{k_i! (t - k_i)!}{t!}\)=\(\displaystyle \sum_{i=1}^w \dfrac{1}{\binom{t}{k_i}} \leq 1 \).

De ello se deduce que

\(\displaystyle \sum_{i=1}^{i=w} \dfrac{1}{\binom{t}{⌈\frac{t}{2}⌉}} \leq 1\).

Así

\(w \leq \dbinom{t}{⌈\frac{t}{2}⌉}\).