6.6: Órdenes de Intervalo

Cuando discutimos el Teorema de Dilworth, comentamos que los aspectos algorítmicos serían diferidos hasta más adelante en el texto. Pero hay una clase importante de pedidos para los que la solución completa es fácil de obtener.

Un poset\(P=(X,P)\) se llama orden de intervalo si existe una función\(I\) asignando a cada elemento\(x \in X\) un intervalo cerrado\(I(x)=[a_x,b_x]\) de la línea real para\(\mathbb{R}\) que para todos\(x, y \in X, x<y\) en\(P\) si y solo si\(b_x<a_y\) en\(\mathbb{R}\). Llamamos a\(I\) una representación de intervalo de\(P\), o simplemente una representación para abreviar. Por brevedad, siempre que digamos que\(I\) es una representación de un orden de intervalo\(P=(X,P)\), usaremos la notación alternativa\([a_x,b_x]\) para el intervalo cerrado\(I(x)\). También, dejamos\(|I(x)|\) denotar la longitud del intervalo, es decir,\(|I(x)|=b_x−a_x\). Volviendo al poset\(P_3\), la representación mostrada en la Figura 6.28 muestra que se trata de un orden de intervalos.

Figura 6.28. Un orden de intervalo y su representación

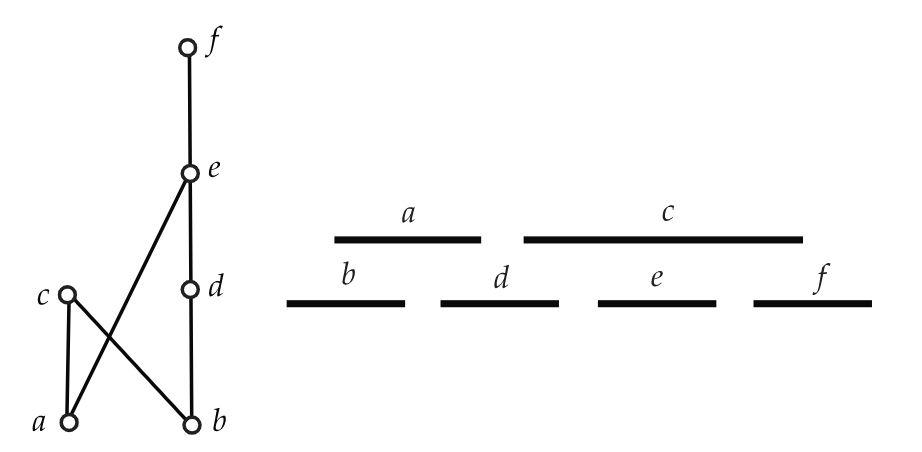
Tenga en cuenta que los puntos finales de los intervalos utilizados en una representación no necesitan ser distintos. De hecho, distintos puntos\(x\) y\(y\) de\(X\) pueden satisfacer\(I(x)=I(y)\). Incluso permitimos intervalos degenerados, es decir, los de la forma\([a,a]\). Por otro lado, se dice que una representación distingue si todos los intervalos son no degenerados y todos los puntos finales son distintos. Es relativamente fácil ver que cada orden de intervalo tiene una representación distintiva.

Como veremos pronto, las órdenes de intervalo se pueden caracterizar sucintamente en términos de citación prohibida. Antes de afirmar esta caracterización, necesitamos introducir un poco más de notación. Por\(n\) (para\(n \geq 1\) un entero), nos referimos a la cadena con\(n\) puntos. Más precisamente, tomamos el terreno establecido para estar\(\{0,1,…,n−1\}\) con\(i<j\) en\(\textbf{n}\) si y solo si\(i<j\) dentro\(Z\). Si\(\textbf{P}=(X,P)\) y\(\textbf{Q}=(Y,Q)\) son posets con\(X\) y\(Y\) disjuntos, entonces\(\textbf{P}+\textbf{Q}\) es el poset\(\textbf{R}=(X \cup Y,R)\) donde el orden parcial se da por\(z \leq w\) en\(R\) si y solo si (a)\(z,w \in X\) y\(z \leq w\) en\(P\) o (b)\(z,w \in Y\) y\(z \leq w\) en\(Q\) . Así,\(\textbf{n}+\textbf{m}\) consiste en una cadena con\(n\) puntos y una cadena con\(m\) puntos y sin comparabilidades entre ellos. En particular, 2+2 puede ser visto como un poset de cuatro puntos con conjunto de suelo\(\{a,b,c,d\}\)\(a<b\) y y\(c<d\) como las únicas relaciones (distintas de las requeridas para hacer reflexiva la relación).

Teorema 6.29. Teorema de Fishburn.

\(\textbf{P}=(X,P)\)Déjese ser un poset. Entonces\(\textbf{P}\) es un orden de intervalo si y sólo si excluye 2+2.

Prueba

Solo mostramos que un orden de intervalo no puede contener un citatorio isomórfico a 2+2, aplazando la prueba en la otra dirección a la siguiente sección. Ahora supongamos que\(\textbf{P}=(X,P)\) es un poset,\(\{x,y,z,w\} \subseteq X\) y el citatorio determinado por estos cuatro puntos es isomórfico a 2+2. Mostramos que no\(\textbf{P}\) es un orden de intervalos. Supongamos al contrario que\(I\) es una representación de intervalo de\(\textbf{P}\). Sin pérdida de generalidad, podemos asumir eso\(x<y\) y\(z<w\) en\(\textbf{P}\). Así\(x‖w\) y\(z‖y\) en\(\textbf{P}\). Entonces\(b_x<a_y\) y\(b_z<a_w\) en\(\mathbb{R}\) eso\(a_w \leq b_x<a_y \leq b_z\), que es una contradicción.